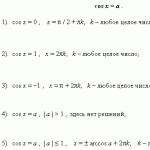Równania trygonometryczne .

Najprostsze równania trygonometryczne .

Metody rozwiązywania równań trygonometrycznych.

Równania trygonometryczne. Równanie zawierające niewiadomą pod nazywamy znak funkcji trygonometrycznej trygonometryczny.

Najprostsze równania trygonometryczne.

Metody rozwiązywania równań trygonometrycznych. Rozwiązanie równania trygonometrycznego składa się z dwóch etapów: transformacja równańżeby to było proste wpisz (patrz wyżej) i rozwiązanieuzyskany najprostszy równanie trygonometryczne. Tam jest siedem podstawowe metody rozwiązywania równań trygonometrycznych.

1. Metoda algebraiczna. Ta metoda jest nam dobrze znana z algebry

(metoda podstawienia zmiennej i metoda podstawienia).

2. Faktoryzacja. Przyjrzyjmy się tej metodzie z przykładami.

PRZYKŁAD 1. Rozwiąż równanie: grzech X+ cos X = 1 .

Rozwiązanie Przenieś wszystkie wyrazy równania w lewo:

Grzech X+ cos X – 1 = 0 ,

Przekształćmy i rozłóżmy wyrażenie na czynniki

Lewa strona równania:

Przykład 2. Rozwiąż równanie: sałata 2 X+ grzech X sałata X = 1.

ROZWIĄZANIE cos2 X+ grzech X sałata X– grzech 2 X– cos 2 X = 0 ,

Grzech X sałata X– grzech 2 X = 0 ,

Grzech X(sałata X– grzech X ) = 0 ,

Przykład 3. Rozwiąż równanie: cos 2 X– cos 8 X+ cos 6 X = 1.

ROZWIĄZANIE cos2 X+ cos 6 X= 1 + cos8 X,

2 cos 4 X cos 2 X= 2 cos² 4 X ,

Cos 4 X · (co 2 X– cos 4 X) = 0 ,

Cos 4 X 2 grzech 3 X grzech X = 0 ,

1). cos 4 X= 0 , 2). grzech 3 X= 0 , 3). grzech X = 0 ,

3.

Przesyłanie do jednolite równanie. Równanie zwany jednorodny od stosunkowo grzech I sałata , Jeśli wszystko warunki tego samego stopnia w odniesieniu do grzech I sałata ten sam kąt. Aby rozwiązać jednorodne równanie, potrzebujesz: A) przesuń wszystkich swoich członków na lewą stronę; B) umieść wszystkie wspólne czynniki poza nawiasami; V) zrównaj wszystkie czynniki i nawiasy do zera; G) nawiasy ustawione na zero dają równanie jednorodne mniejszego stopnia, przez które należy podzielić sałata(Lub grzech) w stopniu wyższym; D) rozwiązać wynikowe równanie algebraiczne względemdębnik . PRZYKŁAD Rozwiąż równanie: 3 grzech 2 X+ 4 grzech X sałata X+ 5 cos 2 X = 2. Rozwiązanie: 3 grzechy 2 X+ 4 grzech X sałata X+ 5 cos 2 X= 2 grzech 2 X+ 2 cos 2 X , Grzech 2 X+ 4 grzech X sałata X+ 3 cos 2 X = 0 , Jasnobrązowy 2 X+ 4opalenizna X + 3 = 0 , stąd y 2 + 4y +3 = 0 , Pierwiastki tego równania to:y 1 = - 1, y 2 = - 3, stąd 1) opalenizna X= –1, 2) brąz X = –3,

4. Przejście do pół rogu. Spójrzmy na tę metodę na przykładzie:

PRZYKŁAD Rozwiąż równanie: 3 grzech X– 5 cos X = 7.

Rozwiązanie: 6 grzechów ( X/ 2) cos( X/ 2) – 5 cos² ( X/ 2) + 5 grzech² ( X/ 2) =

7 grzech² ( X/ 2) + 7 cos² ( X/ 2) ,

2 grzech² ( X/ 2) – 6 grzechów ( X/ 2) cos ( X/ 2) + 12 cos² ( X/ 2) = 0 ,

jasnobrązowy²( X/ 2) – 3 brąz ( X/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Wprowadzenie kąta pomocniczego. Rozważ równanie postaci:

A grzech X + B sałata X = C ,

Gdzie A, B, C– współczynniki;X- nieznany.

Teraz współczynniki równania mają właściwości sinusa i cosinusa, mianowicie: moduł (wartość bezwzględna) każdego z nich

Przykłady:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

Jak rozwiązywać równania trygonometryczne:

Każde równanie trygonometryczne należy sprowadzić do jednego z następujących typów:

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

gdzie \(t\) jest wyrażeniem z x, \(a\) jest liczbą. Takie równania trygonometryczne nazywane są pierwotniaki. Można je łatwo rozwiązać za pomocą () lub specjalnych formuł:

Zobacz infografiki dotyczące rozwiązywania prostych równań trygonometrycznych tutaj: , i .

Przykład . Rozwiąż równanie trygonometryczne \(\sin⁡x=-\)\(\frac(1)(2)\).
Rozwiązanie:

Odpowiedź: \(\left[ \begin(zebrane)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \end(zebrane)\right.\) \(k,n∈Z\)

Co oznacza każdy symbol we wzorze na pierwiastki równań trygonometrycznych, patrz.

Uwaga! Równania \(\sin⁡x=a\) i \(\cos⁡x=a\) nie mają rozwiązań, jeśli \(a ϵ (-∞;-1)∪(1;∞)\). Ponieważ sinus i cosinus dla dowolnego x jest większy lub równy \(-1\) i mniejszy lub równy \(1\):

\(-1≤\sin x≤1\) \(-1≤\cos⁡x≤1\)

Przykład . Rozwiąż równanie \(\cos⁡x=-1,1\).
Rozwiązanie: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Odpowiedź : brak rozwiązań.

Przykład . Rozwiąż równanie trygonometryczne tg\(⁡x=1\).
Rozwiązanie:

Rozwiąż równanie za pomocą koła liczbowego. Dla tego: 1) Zbudujmy krąg) 2) Skonstruuj osie \(x\) i \(y\) oraz oś stycznych (przechodzi ona przez punkt \((0;1)\) równoległy do ​​osi \(y\)). 3) Na osi stycznych zaznacz punkt \(1\). 4) Połącz ten punkt z początkiem - linią prostą. 5) Zanotuj punkty przecięcia tej prostej i okręgu liczbowego. 6)Podpiszmy wartości tych punktów: \(\frac(π)(4)\) ,\(\frac(5π)(4)\) 7) Zapisz wszystkie wartości tych punktów. Ponieważ są dokładnie \(π\) od siebie, wszystkie wartości można zapisać w jednym wzorze:

Odpowiedź: \(x=\)\(\frac(π)(4)\) \(+πk\), \(k∈Z\).

Przykład . Rozwiąż równanie trygonometryczne \(\cos⁡(3x+\frac(π)(4))=0\).
Rozwiązanie:

Użyjmy ponownie koła liczbowego. 1) Skonstruujmy okrąg, osie \(x\) i \(y\). 2) Na osi cosinusa (oś \(x\)) zaznacz \(0\). 3) Narysuj prostopadłą do osi cosinus przechodzącej przez ten punkt. 4) Zaznacz punkty przecięcia prostej i okręgu. 5) Podpiszmy wartości tych punktów: \(-\) \(\frac(π)(2)\),\(\frac(π)(2)\). 6) Wypiszmy całą wartość tych punktów i przyrównajmy je do cosinusa (do tego, co jest wewnątrz cosinusa). \(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\) \(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\) 8) Tradycyjnie \(x\) będziemy wyrażać w równaniach. Pamiętaj, aby traktować liczby za pomocą \(π\) oraz \(1\), \(2\), \(\frac(1)(4)\) itd. Są to te same liczby, co wszystkie inne. Brak dyskryminacji numerycznej! \(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=\)\(\frac(π)(4)\) \(+2πk\) \(|:3\) \(3x=-\)\(\frac(3π)(4)\) \(+2πk\) \(|:3\) \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\)\(+\)\(\frac(2πk)(3)\)

Odpowiedź: \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\) , \(k∈Z\).

Redukcja równań trygonometrycznych do najprostszych to zadanie twórcze, tutaj musisz użyć obu i specjalnych metod rozwiązywania równań:
- Metoda (najpopularniejsza na egzaminie).
- Metoda.
- Metoda argumentów pomocniczych.

Rozważ przykład rozwiązania kwadratowego równania trygonometrycznego

Przykład . Rozwiąż równanie trygonometryczne \(2\cos^2⁡x-5\cos⁡x+2=0\)
Rozwiązanie:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	Dokonajmy zmiany \(t=\cos⁡x\).
	Nasze równanie stało się typowe. Możesz to rozwiązać za pomocą .
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	Dokonujemy wymiany.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	Pierwsze równanie rozwiązujemy za pomocą koła liczbowego. Od tego czasu drugie równanie nie ma rozwiązań \(\cos⁡x∈[-1;1]\) i nie może być równy dwa dla dowolnego x.
	Zapiszmy wszystkie liczby leżące w tych punktach.

Odpowiedź: \(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\).

Przykład rozwiązania równania trygonometrycznego z badaniem ODZ:

Przykład (UŻYCIE) . Rozwiąż równanie trygonometryczne \(=0\)

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Jest ułamek i jest cotangens - więc musisz zapisać. Przypomnę, że cotangens to tak naprawdę ułamek: ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) Dlatego DPV dla ctg\(x\): \(\sin⁡x≠0\).
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\)	Zwróć uwagę na „nierozwiązania” na kole liczbowym.
\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Pozbądźmy się mianownika z równania, mnożąc go przez ctg\(x\). Możemy to zrobić, ponieważ napisaliśmy powyżej, że ctg\(x ≠0\).
\(2\cos^2⁡x-\sin⁡(2x)=0\)	Zastosuj wzór na podwójny kąt dla sinusa: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	Jeśli twoje ręce wyciągnęły się do dzielenia przez cosinus - cofnij je! Możesz dzielić przez wyrażenie ze zmienną, jeśli na pewno nie jest równe zeru (na przykład: \(x^2+1,5^x\)). Zamiast tego wyjmujemy \(\cos⁡x\) z nawiasów.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	Podzielmy równanie na dwa.
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	Pierwsze równanie rozwiązujemy za pomocą koła liczbowego. Podziel drugie równanie przez \(2\) i przesuń \(\sin⁡x\) na prawą stronę.
\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	Korzenie, które się okazały, nie są uwzględnione w ODZ. Dlatego nie będziemy ich spisywać w odpowiedzi. Drugie równanie jest typowe. Podziel przez \(\sin⁡x\) (\(\sin⁡x=0\) nie może być rozwiązaniem równania, ponieważ w tym przypadku \(\cos⁡x=1\) lub \(\cos⁡ x =-1\)).
	Ponownie używamy koła.
\(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\)	Te korzenie nie są wykluczone przez ODZ, więc można je zapisać jako odpowiedź.

Odpowiedź: \(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\).

Pojęcie rozwiązywania równań trygonometrycznych.

• Aby rozwiązać równanie trygonometryczne, przekształć je w jedno lub więcej podstawowych równań trygonometrycznych. Rozwiązanie równania trygonometrycznego ostatecznie sprowadza się do rozwiązania czterech podstawowych równań trygonometrycznych.

Rozwiązywanie podstawowych równań trygonometrycznych.

• Istnieją 4 rodzaje podstawowych równań trygonometrycznych:
• grzech x = a; cos x = a
• brąz x = a; ctg x = a
• Rozwiązywanie podstawowych równań trygonometrycznych polega na spojrzeniu na różne pozycje x na okręgu jednostkowym, a także na użyciu tabeli konwersji (lub kalkulatora).
• Przykład 1. sin x = 0,866. Korzystając z tabeli konwersji (lub kalkulatora), otrzymujesz odpowiedź: x = π/3. Okrąg jednostkowy daje inną odpowiedź: 2π/3. Pamiętaj: wszystkie funkcje trygonometryczne są okresowe, to znaczy ich wartości się powtarzają. Na przykład okresowość sin x i cos x wynosi 2πn, a okresowość tg x i ctg x wynosi πn. Więc odpowiedź jest napisana tak:
• x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
• Przykład 2 cos x = -1/2. Korzystając z tabeli konwersji (lub kalkulatora), otrzymujesz odpowiedź: x = 2π/3. Okrąg jednostkowy daje inną odpowiedź: -2π/3.
• x1 = 2π/3 + 2π; x2 = -2π/3 + 2π.
• Przykład 3. tg (x - π/4) = 0.
• Odpowiedź: x \u003d π / 4 + πn.
• Przykład 4. ctg 2x = 1,732.
• Odpowiedź: x \u003d π / 12 + πn.

Przekształcenia stosowane w rozwiązywaniu równań trygonometrycznych.

• Do przekształcania równań trygonometrycznych stosuje się przekształcenia algebraiczne (rozkład na czynniki, redukcja wyrazów jednorodnych itp.) oraz tożsamości trygonometryczne.
• Przykład 5. Korzystając z tożsamości trygonometrycznych, równanie sin x + sin 2x + sin 3x = 0 przekształca się w równanie 4cos x*sin (3x/2)*cos (x/2) = 0. Zatem następujące podstawowe równania trygonometryczne należy rozwiązać: cos x = 0; grzech(3x/2) = 0; cos(x/2) = 0.

• Znajdowanie kątów ze znanych wartości funkcji.

  • Zanim nauczysz się rozwiązywać równania trygonometryczne, musisz nauczyć się znajdować kąty na podstawie znanych wartości funkcji. Można to zrobić za pomocą tabeli konwersji lub kalkulatora.
  • Przykład: cos x = 0,732. Kalkulator da odpowiedź x = 42,95 stopni. Okrąg jednostkowy da dodatkowe kąty, których cosinus jest również równy 0,732.

• Odłóż rozwiązanie na koło jednostkowe.

  • Możesz umieścić rozwiązania równania trygonometrycznego na okręgu jednostkowym. Rozwiązaniami równania trygonometrycznego na okręgu jednostkowym są wierzchołki wielokąta foremnego.
  • Przykład: Rozwiązania x = π/3 + πn/2 na okręgu jednostkowym są wierzchołkami kwadratu.
  • Przykład: rozwiązaniami x = π/4 + πn/3 na okręgu jednostkowym są wierzchołki sześciokąta foremnego.

• Metody rozwiązywania równań trygonometrycznych.

  • Jeżeli podane równanie trygonometryczne zawiera tylko jedną funkcję trygonometryczną, to równanie to należy rozwiązać jako podstawowe równanie trygonometryczne. Jeżeli dane równanie zawiera dwie lub więcej funkcji trygonometrycznych, to istnieją 2 metody rozwiązania takiego równania (w zależności od możliwości jego przekształcenia).
    • Metoda 1
  • Przekształć to równanie na równanie postaci: f(x)*g(x)*h(x) = 0, gdzie f(x), g(x), h(x) są podstawowymi równaniami trygonometrycznymi.
  • Przykład 6. 2cos x + sin 2x = 0. (0< x < 2π)
  • Rozwiązanie. Używając wzoru na podwójny kąt sin 2x = 2*sin x*cos x, zastąp sin 2x.
  • 2cos x + 2*sin x*cos x = 2cos x*(sin x + 1) = 0. Teraz rozwiąż dwa podstawowe równania trygonometryczne: cos x = 0 i (sin x + 1) = 0.
  • Przykład 7 cos x + cos 2x + cos 3x = 0. (0< x < 2π)
  • Rozwiązanie: Korzystając z tożsamości trygonometrycznych, przekształć to równanie w równanie postaci: cos 2x(2cos x + 1) = 0. Teraz rozwiąż dwa podstawowe równania trygonometryczne: cos 2x = 0 i (2cos x + 1) = 0.
  • Przykład 8. grzech x - grzech 3x \u003d cos 2x. (0< x < 2π)
  • Rozwiązanie: Korzystając z tożsamości trygonometrycznych, przekształć to równanie w równanie postaci: -cos 2x*(2sin x + 1) = 0. Teraz rozwiąż dwa podstawowe równania trygonometryczne: cos 2x = 0 i (2sin x + 1) = 0.
    • Metoda 2
  • Zamień podane równanie trygonometryczne na równanie zawierające tylko jedną funkcję trygonometryczną. Następnie zastąp tę funkcję trygonometryczną jakąś niewiadomą, na przykład t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x/2) = t itd.).
  • Przykład 9. 3sin^2 x - 2cos^2 x = 4sin x + 7 (0< x < 2π).
  • Rozwiązanie. W tym równaniu zastąp (cos^2 x) przez (1 - sin^2 x) (zgodnie z tożsamością). Przekształcone równanie wygląda następująco:
  • 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Zamień sin x na t. Teraz równanie wygląda następująco: 5t^2 - 4t - 9 = 0. To jest równanie kwadratowe z dwoma pierwiastkami: t1 = -1 i t2 = 9/5. Drugi pierwiastek t2 nie spełnia zakresu funkcji (-1< sin x < 1). Теперь решите: t = sin х = -1; х = 3π/2.
  • Przykład 10. tg x + 2 tg^2 x = ctg x + 2
  • Rozwiązanie. Zastąp tgx przez t. Przepisz oryginalne równanie w następujący sposób: (2t + 1)(t^2 - 1) = 0. Teraz znajdź t, a następnie znajdź x dla t = tg x.

• Specjalne równania trygonometryczne.

  • Istnieje kilka specjalnych równań trygonometrycznych, które wymagają określonych przekształceń. Przykłady:
  • a*grzech x+ b*cos x = do ; a(sin x + cos x) + b*cos x*sin x = c;
  • a*sin^2 x + b*sin x*cos x + c*cos^2 x = 0

• Okresowość funkcji trygonometrycznych.

  • Jak wspomniano wcześniej, wszystkie funkcje trygonometryczne są okresowe, to znaczy ich wartości powtarzają się po pewnym okresie. Przykłady:
    • Okres funkcji f(x) = sin x wynosi 2π.
    • Okres funkcji f(x) = tg x jest równy π.
    • Okres funkcji f(x) = sin 2x jest równy π.
    • Okres funkcji f(x) = cos(x/2) wynosi 4π.
  • Jeśli w zadaniu określony jest okres, oblicz wartość x w tym okresie.
  • Uwaga: Rozwiązywanie równań trygonometrycznych nie jest łatwym zadaniem i często prowadzi do błędów. Sprawdź więc dokładnie swoje odpowiedzi. Aby to zrobić, możesz użyć kalkulatora graficznego do wykreślenia podanego równania R(x) = 0. W takich przypadkach rozwiązania będą reprezentowane jako ułamki dziesiętne (to znaczy π jest zastępowane przez 3,14).

Równania trygonometryczne

Rozwiązywanie najprostszych równań trygonometrycznych

Stopnie i radiany

Wprowadzenie do koła trygonometrycznego

Obroty na okręgu trygonometrycznym

Ile bólu wiąże się ze słowem trygonometria. Ten temat pojawia się w 9 klasie i nigdzie nie zniknął. Trudno jest tym, którzy czegoś nie rozumieją od razu. Spróbujmy to naprawić, aby rozjaśnić twarz uśmiechem na słowo trygonometria lub przynajmniej uzyskać „pokerową twarz”.

Zacznijmy od tego, że tak jak długość można wyrazić w metrach lub milach, tak też można kąt można wyrazić w radianach lub stopniach.

1 radian = 180/π ≈ 57,3 stopnia

Ale łatwiej jest zapamiętać liczby całkowite: 3,14 radiana = 180 stopni. Wszystkie są tą samą wartością liczby π.

Przypomnijmy, że jeśli każą nam się odwrócić, to musimy obrócić się o 180 stopni, a teraz możemy też powiedzieć: Obróć π!

O wykresach sinusa, cosinusa i tange porozmawiamy w innym artykule.

A teraz zacznijmy od kartezjańskiego (prostokątnego) układu współrzędnych.

Wcześniej pomagała budować wykresy, a teraz pomoże z sinusem i cosinusem.

Na przecięciu osi X i osi Y konstruujemy okrąg jednostkowy (promień 1):

Następnie oś cosinusa będzie pokrywać się z x, oś sinusoidy z y. Na rysunku pokazano również osie stycznych i cotangensów.

A teraz odnotowujemy główne wartości stopni i radianów na okręgu.

załóżmy zgodzimy się z tobą, jako dorośli: na okręgu zaznaczymy kąt w radianach, czyli przez Pi.

Wystarczy pamiętać, że π = 180°(wtedy π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

Teraz zakręćmy się w kółko! Zwyczajowo przyjmuje się najbardziej wysunięty na prawo punkt okręgu (gdzie 0 °) jako początek raportu:

Z niej wyznaczamy dalszy zakręt. Możemy obracać zarówno w kierunku dodatnim (przeciwnie do ruchu wskazówek zegara), jak iw kierunku ujemnym (zgodnie z ruchem wskazówek zegara).

Istnieją dwa sposoby obrócenia o 45°: przez lewe ramię o 45° w stronę (+) lub przez prawe ramię o 315° w stronę (-).

Najważniejsze jest kierunek, w którym będziemy patrzeć, a nie kąt!

Konieczne jest skierowanie linii przerywanej na 100 punktów, a ile obrotów i w jakim kierunku wykonamy wokół siebie - to nie ma znaczenia!

Możesz zdobyć 100 punktów, obracając o 135° lub 360°+135°, lub -225°, lub -225°-360°...

A teraz masz dwa sposoby:

Naucz się całego koła (trygonometru). Dobra opcja, jeśli wszystko jest w porządku z twoją pamięcią i nic nie wyfrunie ci z głowy w kluczowym momencie:

Możesz zapamiętać kilka rogów tabeli i odpowiadające im wartości, a następnie ich użyć.

Znajdź równe kąty (pionowe, odpowiadające) na okręgu trygonometrycznym. Możesz dostać się do dowolnego punktu, używając sumy lub różnicy dwóch wartości tabelarycznych.

Spróbujmy to zrozumieć na przykładzie:

Przykład 1. cos(x) = ½

1) Pamiętaj, że oś cos(x) jest osią poziomą. Zaznaczamy na nim wartość ½ i rysujemy prostopadłą (fioletową) linię prostą do przecięć z okręgiem.

2) Mam dwa punkty przecięcia z okręgiem, wartość tych kątów będzie rozwiązaniem równania.

Chodzi o to, aby znaleźć te rogi.

Lepiej obejść się „małym krwią” i poznać wartość sinusa i cosinusa dla kątów od 30° do 60°.

Lub zapamiętaj tę sztuczkę:

Ponumeruj palce od 0 do 4 od małego do kciuka. Kąt jest ustawiany między małym palcem a dowolnym innym palcem (od 0 do 90).

Na przykład, wymagane jest znalezienie grzechu (π/2): π / 2 to kciuk, n = 4 jest podstawiane do wzoru na sinus: grzech(π/2) = √4/2 = 1 => grzech(π/2) = 1.

cos(π/4) - ? π/4 odpowiada środkowemu palcowi (n = 2) => cos(π/4) = √2/2.

Przy wartości cos (x) = ½ z tabeli lub korzystając z reguły mnemotechnicznej, znajdujemy x = 60° (pierwszy punkt x = + π / 3 ze względu na to, że obrót był przeciwny do ruchu wskazówek zegara (+), kąt wynosi zaznaczone czarnym łukiem).

Drugi punkt odpowiada dokładnie temu samemu kątowi, tylko obrót będzie zgodny z ruchem wskazówek zegara (-). x = −π/3 (kąt jest pokazany przez dolny czarny łuk).

I ostatnie, zanim w końcu odkryjesz tajemną wiedzę o trygonometrii:

Kiedy wymagane jest trafienie "100 punktów", możemy je uderzyć, obracając się do...=-225°=135°=495°=...

Tak samo tutaj! Różne kąty mogą odzwierciedlać ten sam kierunek.

Możesz absolutnie powiedzieć, że musisz skręcić pod wymaganym kątem, a następnie możesz obrócić o 360 ° = 2π (na niebiesko) tyle razy, ile chcesz iw dowolnym kierunku.

W ten sposób można dostać się w pierwszy kierunek 60°: ...,60°-360°, 60°, 60°+360°,...

A jak zapisać resztę kątów, żeby nie zapisać nieskończonej ilości punktów? (Chciałbym to zobaczyć☻)

Dlatego poprawne jest zapisanie odpowiedzi: x = 60 + 360n, gdzie n jest liczbą całkowitą (n∈Ζ) (obracamy o 60 stopni, a następnie okrążamy tyle razy, ile chcemy, najważniejsze jest to, że kierunek pozostaje takie samo). Podobnie x = −60 + 360n.

Ale zgodziliśmy się, że wszystko na okręgu jest zapisane przez π, więc cos(x) = ½ dla x=π/3 + 2πn, n∈Z i x = −π/3 + 2πk, k∈Z.

Odpowiedź: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Z.

Przykład nr 2. 2sinx = √2

Pierwszą rzeczą do zrobienia jest przesunięcie 2 w prawo => sinx=√2/2

1) sin(x) pokrywa się z osią Y. Na osi sin(x) zaznacz √2/2 i narysuj ⊥ fioletowa prosta do przecięcia z okręgiem.

2) Z tabeli sinx = √2/2 w punkcie x = π/4, a drugiego punktu będziemy szukać obracając się do π, a następnie musimy wrócić z powrotem do π/4.

Zatem drugim punktem będzie x = π − π/4 = 3π/4, można do niego również dotrzeć za pomocą czerwonych strzałek lub w inny sposób.

I nie zapomnijmy dodać +2πn, n∈Ζ.

Odpowiedź: 3π/4 + 2πn i π/4 + 2πk, k i n są dowolnymi liczbami całkowitymi.

Przykład nr 3. tg(x + π/4) = √3

Wszystko wydaje się być poprawne, tangens jest równy liczbie, ale pi / 4 w tangensie myli. Następnie dokonujemy podstawienia: y = x + π/4.

tg(y) = √3 nie wygląda już tak źle. Pamiętajmy, gdzie jest oś stycznych.

1) I teraz na osi stycznych odnotowujemy wartość √3, która jest większa od 1.

2) Narysuj fioletową linię przechodzącą przez wartość √3 i początek układu współrzędnych. Ponownie na przecięciu z okręgiem uzyskuje się 2 punkty.

Zgodnie z regułą mnemoniczną, przy tangensie √3, pierwszą wartością jest π/3.

3) Aby dostać się do drugiego punktu, możesz dodać π => y = π/3 + π = 4π/3 do pierwszego punktu (π/3).

4) Ale znaleźliśmy tylko y , z powrotem do x. y = π/3 + 2πn i y = x + π/4, wtedy x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Z.

Drugi pierwiastek: y = 4π/3 + 2πk i y = x + π/4, wtedy x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Teraz korzenie na okręgu będą tutaj:

Odpowiedź: π/12 + 2πn i 13π/12 + 2πk, k i n- dowolne liczby całkowite.

Oczywiście te dwie odpowiedzi można połączyć w jedną. Od 0 obróć o π / 12, a następnie każdy pierwiastek powtórzy się co π (180 °).

Odpowiedź można również zapisać następująco: π/12 + πn, n∈Z.

Przykład 4: −10ctg(x) = 10

Przenieśmy (−10) do innej części: ctg(x) = −1. Zwróć uwagę na wartość -1 na osi cotangensów.

1) Narysuj linię prostą przechodzącą przez ten punkt i początek.

2) Będziemy musieli ponownie pamiętać, kiedy dzielenie cosinusa przez sinusa da jednostkę (otrzymuje się to za pomocą π / 4). Ale tutaj -1, więc jednym punktem będzie -π/4. A drugi znajdujemy obracając w górę do π, a następnie z powrotem o π/4 (π − π/4).

Można to zrobić inaczej (na czerwono), ale moja rada dla ciebie: zawsze licz od całkowitych wartości pi(π, 2π, 3π...) o wiele mniej prawdopodobne, że się pomylisz.

Nie zapomnij dodać 2πk do każdego punktu.

Odpowiedź: 3π/4 + 2πn i −π/4 + 2πk, k i n są dowolnymi liczbami całkowitymi.

Algorytm rozwiązywania równań trygonometrycznych (na przykład cos(x) = − √ 3/2) :

1. Wartość (−√3/2) zaznaczamy na osi funkcji trygonometrycznej (cosinusy, to jest oś X).
2. Rysujemy linię prostopadłą do osi (cosinusy) do przecięć z okręgiem.
3. Punkty przecięcia z okręgiem będą pierwiastkami równania.
4. Wartość jednego punktu (bez względu na to, jak się do tego dostaniesz)+2 szt.

Podstawy wystarczą, zanim przejdziesz dalej, utrwal zdobytą wiedzę.

Rozdział 15

15.6. Rozwiązywanie bardziej złożonych równań trygonometrycznych

W poprzednich paragrafach 3-5 podano rozwiązania najprostszych równań trygonometrycznych , , i. Bardziej złożone równania trygonometryczne zawierające kilka funkcji trygonometrycznych o tych samych lub różnych argumentach są do nich redukowane za pomocą identycznych przekształceń lub przez rozwiązanie pomocniczego równania algebraicznego.

Ogólna technika rozwiązywania takich równań polega na zastąpieniu wszystkich funkcji trygonometrycznych zawartych w równaniu przez jedną funkcję opartą na wzorach łączących te funkcje. Rozwiązując równanie dążymy do takich przekształceń, które prowadzą do równań równoważnych danemu. W przeciwnym razie musisz sprawdzić uzyskane korzenie.

Utrata korzeni to częsty błąd. Inne takie błędy to niedokładna znajomość wzorów do rozwiązywania najprostszych równań, a także niemożność prawidłowego znalezienia pożądanej wartości funkcji łuku.

Rozważ przykłady.

Rozwiązać równanie.

Przykład 2. (przykład redukcji do jednego argumentu).

Rozwiązać równanie.

Rozwiązanie:
Wskazane jest przejście do argumentacji. Produkt przypomina wzór na sinus podwójnego argumentu: .
Podstawiając do równania otrzymujemy: .
Po lewej stronie ponownie zastosuj wzór na sinus podwójnego argumentu, ale najpierw pomnóż obie strony równania przez.
; ; .
Otrzymaliśmy najprostsze równanie typu i przyrównujemy cały argument do rozwiązania najprostszego równania:
, Gdzie .

Rozwiązać równanie.

Rozwiązanie:
Według jednego ze wzorów na obniżenie stopnia otrzymujemy .

Po podstawieniu do równania mamy

Rozwiązać równanie.

Rozwiązanie:
Przechodząc na prawą stronę, otrzymujemy , co jest równe:
; ; .
Tutaj musieliśmy przejść przez podniesienie stopnia równania, ale otrzymaliśmy możliwość zastosowania dobrego rozwiązania - przenieś wszystkie wyrazy do jednej części i rozłóż wynikowe wyrażenie na czynniki:
.
Przyrównując każdy czynnik z osobna do zera, otrzymujemy układ równań,

co z reguły jest równoważne podanemu równaniu (wyjątek od tej reguły rozpatrzono w poniższym przykładzie).
Rozwiązujemy równanie, mamy
, I .
Rozwiązujemy równanie lub , mamy , i .

Rozwiązać równanie.

Włączenie obcego korzenia do odpowiedzi jest uważane za błąd. Aby tego uniknąć, należy upewnić się, że otrzymane pierwiastki nie anulują żadnej z funkcji znajdujących się w mianowniku ułamka danego równania (jeśli występują ułamki) oraz że przy tych pierwiastkach żadna z funkcji w oryginale równanie traci sens (jeśli są uwzględnione). Należy pamiętać, przy jakich wartościach argumentu funkcja znika i dziedzina definicji każdej funkcji trygonometrycznej. Przez analogię mówią o dziedzinie równania (dziedzinie akceptowalnych wartości, czyli ODZ, nieznanego) . Dziedziną definicji równania trygonometrycznego jest część wspólna (przecięcie) dziedzin definicji lewej i prawej części tego równania. Jeśli wynikowy pierwiastek nie należy do dziedziny równania, to jest outsiderem i musi zostać odrzucony.

Rozwiązać równanie
.

Rozwiązanie:
Przejdźmy do jednej funkcji. Jeśli wyrażone przez , to otrzymamy irracjonalne równanie, co jest niepożądane. Zamieńmy na:
; .
Otrzymane równanie rozwiązujemy jako kwadratowe względem .
Lub .
Równanie nie ma pierwiastków.
Dla równania mamy:
. Ale oznaczają one również te same liczby nieparzyste, więc zapisujemy rozwiązanie w prostszy sposób: .

Rozwiązać równanie
.

Aby uzyskać jednorodne równanie (wszystkie wyrazy tego samego stopnia - drugi), mnożymy prawą stronę przez wyrażenie, które jest równe.
;
.
Ponieważ pierwiastki równania nie są pierwiastkami równania pierwotnego (można to łatwo sprawdzić przez podstawienie), to aby przejść do jednej funkcji, dzielimy obie części równania przez .

Rozwiązujemy równanie kwadratowe dla .
Lub .
Dla równania mamy: .
Dla równania otrzymujemy .

Rozwiązać równanie.

Wyrażamy przez i , dostajemy
. Tutaj musi być różny od zera (w przeciwnym razie równanie traci sens), więc dziedziną równania jest all . Skoro , to mnożymy obie strony równania przez, żeby pozbyć się ułamków.
;
;
.
Dla równania mamy