Jaki jest wzór na obliczenie pędu ciała? Pojęcie pędu ciała

Po przestudiowaniu praw Newtona widzimy, że za ich pomocą można rozwiązać główne problemy mechaniki, jeśli znamy wszystkie siły działające na ciało. Są sytuacje, w których określenie tych wielkości jest trudne lub wręcz niemożliwe. Rozważmy kilka takich sytuacji.Kiedy zderzają się dwie kule bilardowe lub samochody, możemy stwierdzić o działających siłach, że taka jest ich natura, działają tutaj siły sprężyste. Nie będziemy jednak w stanie dokładnie ustalić ani ich modułów, ani ich kierunków, zwłaszcza że siły te mają niezwykle krótki czas działania.W ruchu rakiet i samolotów odrzutowych również niewiele możemy powiedzieć o siłach, które wprawiają te ciała w ruch.W takich przypadkach stosuje się metody, które pozwalają uniknąć rozwiązywania równań ruchu i natychmiast wykorzystać konsekwencje tych równań. Jednocześnie wprowadzane są nowe wielkości fizyczne. Rozważmy jedną z tych wielkości, zwaną pędem ciała

Strzała wystrzelona z łuku. Im dłuższy kontakt cięciwy ze strzałą (∆t), tym większa zmiana pędu strzały (∆), a co za tym idzie, większa jej prędkość końcowa.

Dwie zderzające się kule. Kiedy kule się stykają, działają na siebie z równymi siłami, jak uczy nas trzecie prawo Newtona. Oznacza to, że zmiany ich pędów również muszą być równe w wartości bezwzględnej, nawet jeśli masy kulek nie są równe.

Po przeanalizowaniu wzorów można wyciągnąć dwa ważne wnioski:

1. Te same siły działające w tym samym czasie powodują takie same zmiany pędu różnych ciał, niezależnie od masy tych ostatnich.

2. Tę samą zmianę pędu ciała można osiągnąć albo działając małą siłą przez długi czas, albo działając przez krótki czas dużą siłą na to samo ciało.

Zgodnie z drugim prawem Newtona możemy napisać:

∆t = ∆ = ∆ / ∆t

Stosunek zmiany pędu ciała do okresu czasu, w którym ta zmiana nastąpiła, jest równy sumie sił działających na to ciało.

Po przeanalizowaniu tego równania widzimy, że drugie prawo Newtona pozwala rozszerzyć klasę problemów do rozwiązania o problemy, w których masa ciał zmienia się w czasie.

Jeśli spróbujemy rozwiązać problemy ze zmienną masą ciał, używając zwykłego sformułowania drugiego prawa Newtona:

wtedy próba takiego rozwiązania doprowadziłaby do błędu.

Przykładem tego jest wspomniany już samolot odrzutowy czy rakieta kosmiczna, które podczas ruchu spalają paliwo, a produkty tego spalonego materiału wyrzucane są w otaczającą przestrzeń. Naturalnie masa samolotu lub rakiety maleje wraz ze zużyciem paliwa.

Pomimo tego, że drugie prawo Newtona w postaci „siła wypadkowa jest równa iloczynowi masy ciała i jego przyspieszenia” pozwala rozwiązać dość szeroką klasę problemów, to jednak istnieją przypadki ruchu ciała, których nie da się w pełni opisać tym równaniem . W takich przypadkach konieczne jest zastosowanie innego sformułowania drugiego prawa, które wiąże zmianę pędu ciała z pędem siły wypadkowej. Ponadto istnieje szereg problemów, w których rozwiązanie równań ruchu jest matematycznie niezwykle trudne lub wręcz niemożliwe. W takich przypadkach przydatne jest dla nas użycie pojęcia pędu.

Wykorzystując prawo zachowania pędu i związek między pędem siły a pędem ciała, możemy wyprowadzić drugie i trzecie prawo Newtona.

Drugie prawo Newtona wywodzi się ze stosunku pędu siły do ​​pędu ciała.

Impuls siły jest równy zmianie pędu ciała:

Po wykonaniu odpowiednich przeniesień otrzymamy zależność siły od przyspieszenia, ponieważ przyspieszenie definiujemy jako stosunek zmiany prędkości do czasu, w którym ta zmiana nastąpiła:

Podstawiając wartości do naszego wzoru, otrzymujemy wzór na drugie prawo Newtona:

Aby wyprowadzić trzecie prawo Newtona, potrzebujemy prawa zachowania pędu.

Wektory podkreślają wektorowy charakter prędkości, to znaczy fakt, że prędkość może zmieniać kierunek. Po przekształceniach otrzymujemy:

Ponieważ przedział czasu w układzie zamkniętym był wartością stałą dla obu ciał, możemy napisać:

Otrzymaliśmy trzecie prawo Newtona: dwa ciała oddziałują na siebie siłami o równych wartościach i przeciwnych kierunkach. Wektory tych sił są skierowane odpowiednio do siebie, moduły tych sił są równe pod względem wartości.

Bibliografia

1. Tichomirowa SA, Jaworski B.M. Fizyka (poziom podstawowy) - M.: Mnemozina, 2012.
2. Gendenstein LE, Dick Yu.I. Fizyka klasa 10. - M.: Mnemosyne, 2014.
3. Kikoin I.K., Kikoin A.K. Fizyka - 9, Moskwa, Edukacja, 1990.

Praca domowa

1. Zdefiniuj pęd ciała, pęd siły.
2. Jaki związek ma pęd ciała z pędem siły?
3. Jakie wnioski można wyciągnąć ze wzorów na pęd ciała i pęd siły?

1. Portal internetowy Pytania-fizyka.ru ().
2. Portal internetowy Frutmrut.ru ().
3. Portal internetowy Fizmat.by ().

Jeśli na ciele o masie m przez pewien okres czasu Δ t siła F → działa, to następuje zmiana prędkości ciała ∆ v → = v 2 → - v 1 →. Otrzymujemy to w czasie Δ t ciało nadal porusza się z przyspieszeniem:

za → = ∆ v → ∆ t = v 2 → - v 1 → ∆ t .

Na podstawie podstawowego prawa dynamiki, czyli drugiego prawa Newtona, mamy:

fa → = m za → = m v 2 → - v 1 → ∆ t lub fa → ∆ t = m v 2 → - m v 1 → = m ∆ v → = ∆ m v → .

pęd ciała, Lub ilość ruchu jest wielkością fizyczną równą iloczynowi masy ciała i prędkości jego ruchu.

Pęd ciała jest uważany za wielkość wektorową, która jest mierzona w kilogramometrach na sekundę (k g m / s).

Definicja 2

Impuls siły- Jest to wielkość fizyczna równa iloczynowi siły i czasu jej działania.

Pęd jest określany jako wielkości wektorowe. Istnieje inne sformułowanie definicji.

Definicja 3

Zmiana pędu ciała jest równa pędowi siły.

Z pędem oznaczonym p → Drugie prawo Newtona jest zapisane jako:

fa → ∆t = ∆p → .

Ta forma pozwala nam sformułować drugie prawo Newtona. Siła F → jest wypadkową wszystkich sił działających na ciało. Równość jest zapisywana jako rzuty na osie współrzędnych widoku:

fa x Δ t = Δ p x ; fa y ∆t = ∆p y ; Fz ∆t = ∆pz .

Obrazek 1 . 16 . 1. Model pędu ciała.

Zmiana rzutu pędu ciała na dowolną z trzech wzajemnie prostopadłych osi jest równa rzutowi impulsu siły na tę samą oś.

Definicja 4

Ruch jednowymiarowy jest ruchem ciała wzdłuż jednej z osi współrzędnych.

Przykład 1

Jako przykład rozważmy swobodny spadek ciała z prędkością początkową v 0 pod działaniem grawitacji w okresie czasu t. Gdy kierunek osi O Y jest skierowany pionowo w dół, pęd grawitacji F t \u003d mg, działający w czasie t, jest równy m g t. Taki impuls jest równy zmianie pędu ciała:

F t t \u003d m g t \u003d Δ p \u003d m (v - v 0), skąd v \u003d v 0 + g t.

Wpis pokrywa się z kinematycznym wzorem na wyznaczenie prędkości ruchu jednostajnie przyspieszonego. Moduł siły nie zmienia się od całego przedziału t. Gdy jest zmienna co do wielkości, to wzór na pęd wymaga podstawienia średniej wartości siły F przez p z przedziału czasu t. Obrazek 1 . 16 . 2 pokazuje, jak wyznacza się pęd siły zależnej od czasu.

Obrazek 1 . 16 . 2. Obliczenie impulsu siły z wykresu F (t)

Konieczne jest wybranie przedziału Δ t na osi czasu, jasne jest, że siła F(t) praktycznie bez zmian. Impuls siły F (t) Δ t przez okres czasu Δt będzie równy polu zacienionej figury. Podczas dzielenia osi czasu na przedziały przez Δ t i na przedziale od 0 do t dodaj impulsy wszystkich działających sił z tych przedziałów Δ t i , wtedy całkowity impuls siły będzie równy obszarowi formacji przy użyciu osi schodkowej i czasu.

Stosując granicę (Δ t i → 0) , możesz znaleźć obszar, który będzie ograniczony przez wykres F(t) i oś t. Korzystanie z definicji impulsu siły z rozkładu ma zastosowanie do dowolnych praw, w których występują zmieniające się siły i czas. Takie rozwiązanie prowadzi do integracji funkcji F(t) z przedziału [ 0 ; T] .

Obrazek 1 . 16 . 2 pokazuje impuls siły, który mieści się w przedziale od t 1 = 0 s do t 2 = 10 .

Ze wzoru otrzymujemy to F c p (t 2 - t 1) \u003d 1 2 F m a x (t 2 - t 1) \u003d 100 N s \u003d 100 kg m / s.

Oznacza to, że przykład pokazuje F z p \u003d 1 2 F m a x \u003d 10 N.

Istnieją przypadki, gdy wyznaczenie średniej siły F z p jest możliwe przy znanym czasie i danych o podanym pędzie. Przy silnym uderzeniu w piłkę o masie 0,415 kg można zgłosić prędkość równą v \u003d 30 m / s. Przybliżony czas uderzenia to 8 10 – 3 s.

Wówczas wzór na pęd przyjmuje postać:

p = m v = 12,5 kg·m/s.

Aby określić średnią siłę F c p podczas uderzenia, konieczne jest F c p = p ∆ t = 1,56 10 3 N.

Otrzymaliśmy bardzo dużą wartość, która jest równa ciału o masie 160 kg.

Kiedy ruch odbywa się po zakrzywionej ścieżce, wówczas wartość początkowa p 1 → i końcowa
p 2 → może różnić się modułem i kierunkiem. Aby wyznaczyć pęd ∆ p → skorzystaj z diagramu pędu, na którym są wektory p 1 → i p 2 → , oraz ∆ p → = p 2 → - p 1 → zbudowane zgodnie z zasadą równoległoboku.

Przykład 2

Rysunek 1 jest pokazany jako przykład. 16 . 2, gdzie narysowano wykres impulsów piłki odbijającej się od ściany. Podczas serwowania piłka o masie m z prędkością v 1 → uderza w powierzchnię pod kątem α do normalnej i odbija się od niej z prędkością v 2 → pod kątem β . Podczas uderzenia w ścianę na piłkę działa siła F → skierowana w taki sam sposób, jak wektor ∆ p → .

Obrazek 1 . 16 . 3 . Odbicie piłki od szorstkiej ściany i diagram pędu.

Jeśli następuje normalny spadek piłki o masie m na sprężystą powierzchnię z prędkością v 1 → = v → , to po odbiciu zmieni się ona na v 2 → = - v → . Oznacza to, że przez pewien okres czasu pęd będzie się zmieniał i będzie równy ∆ p → = - 2 m v → . Korzystając z rzutów na ОХ, wynik zostanie zapisany jako Δ p x = – 2 m v x . Z rysunku 1 . 16 . 3 widać, że oś ОХ jest skierowana od ściany, wtedy v x< 0 и Δ p x >0 . Ze wzoru wynika, że ​​modułowi Δ p towarzyszy moduł prędkości, który przyjmuje postać Δ p = 2 m v .

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Zmieniają się, ponieważ siły interakcji działają na każde z ciał, ale suma impulsów pozostaje stała. To się nazywa prawo zachowania pędu.

Drugie prawo Newtona wyrażone wzorem. Można to zapisać inaczej, pamiętając, że przyspieszenie jest równe szybkości zmiany prędkości ciała. Dla ruchu jednostajnie przyspieszonego wzór będzie wyglądał następująco:

Jeśli podstawimy to wyrażenie do wzoru, otrzymamy:

,

Formułę tę można przepisać jako:

Zmiana iloczynu masy ciała i jego prędkości jest zapisana po prawej stronie tego równania. Iloczyn masy ciała i prędkości to wielkość fizyczna tzw pęd ciała Lub ilość ruchu ciała.

pęd ciała nazywa się iloczynem masy ciała i jego prędkości. Jest to wielkość wektorowa. Kierunek wektora pędu pokrywa się z kierunkiem wektora prędkości.

Innymi słowy, ciało o masie M poruszający się z prędkością ma pęd. Jednostką pędu w układzie SI jest pęd ciała o masie 1 kg poruszającego się z prędkością 1 m/s (kg m/s). Kiedy dwa ciała oddziałują na siebie, jeśli pierwsze działa na drugie z siłą, to zgodnie z trzecim prawem Newtona drugie działa z siłą na pierwsze. Oznaczmy masy tych dwóch ciał jako M 1 i M 2 oraz ich prędkości względem dowolnego układu odniesienia poprzez i . Nadgodziny T w wyniku wzajemnego oddziaływania ciał ich prędkości zmienią się i wyrównają i . Podstawiając te wartości do wzoru, otrzymujemy:

,

,

Stąd,

Zamieńmy znaki obu stron równości na przeciwne i zapiszmy ją w postaci

Po lewej stronie równania – suma impulsów początkowych dwóch ciał, po prawej – suma impulsów tych samych ciał po czasie T. Kwoty są równe. Więc pomimo tego. że pęd każdego ciała zmienia się podczas interakcji, całkowity pęd (suma pędów obu ciał) pozostaje niezmieniony.

Jest to również ważne, gdy kilka ciał oddziałuje na siebie. Jednak ważne jest, aby te ciała oddziaływały tylko ze sobą i aby nie działały na nie siły innych ciał, które nie wchodzą w skład układu (lub aby siły zewnętrzne były zrównoważone). Nazywa się grupę ciał, która nie oddziałuje z innymi ciałami zamknięty system dotyczy tylko systemów zamkniętych.

Pęd w fizyce

W tłumaczeniu z łaciny „impuls” oznacza „pchnięcie”. Ta wielkość fizyczna jest również nazywana „pędem”. Został wprowadzony do nauki mniej więcej w tym samym czasie, kiedy odkryto prawa Newtona (pod koniec XVII wieku).

Dziedziną fizyki badającą ruch i oddziaływanie ciał materialnych jest mechanika. Impuls w mechanice jest wielkością wektorową równą iloczynowi masy ciała i jego prędkości: p=mv. Kierunki wektorów pędu i prędkości zawsze pokrywają się.

W układzie SI za jednostkę pędu przyjmuje się pęd ciała o masie 1 kg, które porusza się z prędkością 1 m/s. Dlatego jednostką pędu w układzie SI jest 1 kg∙m/s.

W problemach obliczeniowych uwzględniane są rzuty wektorów prędkości i pędu na dowolną oś i stosowane są równania dla tych rzutów: na przykład, jeśli wybrana jest oś x, wówczas uwzględniane są rzuty v(x) i p(x). Z definicji pędu wielkości te są powiązane zależnością: p(x)=mv(x).

W zależności od tego, która oś jest wybrana i gdzie jest skierowana, rzut wektora pędu na nią może być dodatni lub ujemny.

Prawo zachowania pędu

Impulsy ciał materialnych mogą się zmieniać podczas ich fizycznego oddziaływania. Na przykład, gdy zderzają się dwie kule zawieszone na nitkach, ich pędy zmieniają się wzajemnie: jedna kula może rozpocząć ruch ze stanu stacjonarnego lub zwiększyć swoją prędkość, a druga przeciwnie, zmniejszyć prędkość lub zatrzymać się. Jednak w systemie zamkniętym, tj. gdy ciała oddziałują tylko ze sobą i nie są wystawione na działanie sił zewnętrznych, suma wektorów impulsów tych ciał pozostaje stała podczas dowolnego ich oddziaływania i ruchu. To jest prawo zachowania pędu. Matematycznie można to wyprowadzić z praw Newtona.

Prawo zachowania pędu ma również zastosowanie do takich układów, w których na ciała działają pewne siły zewnętrzne, ale ich suma wektorów jest równa zeru (np. grawitacja jest równoważona przez siłę sprężystości powierzchni). Konwencjonalnie taki system można również uznać za zamknięty.

W formie matematycznej prawo zachowania pędu można zapisać następująco: p1+p2+…+p(n)=p1’+p2’+…+p(n)’ (pędy p są wektorami). W przypadku układu dwóch ciał to równanie wygląda następująco: p1+p2=p1'+p2' lub m1v1+m2v2=m1v1'+m2v2'. Na przykład w rozważanym przypadku z kulkami sumaryczny pęd obu piłek przed oddziaływaniem będzie równy całkowitemu pędowi po oddziaływaniu.

PULS CIAŁA

Pęd ciała jest fizyczną wielkością wektorową równą iloczynowi masy ciała i jego prędkości.

Wektor pędu ciało jest skierowane w taki sam sposób jak wektor prędkości to ciało.

Przez impuls układu ciał rozumie się sumę impulsów wszystkich ciał tego układu: ∑p=p 1 +p 2 +... . Prawo zachowania pędu: w zamkniętym układzie ciał, w dowolnym procesie, jego pęd pozostaje niezmieniony, tj. ∑p = stała

(Układ zamknięty to układ ciał, które oddziałują tylko ze sobą i nie oddziałują z innymi ciałami).

Pytanie 2. Termodynamiczna i statystyczna definicja entropii. Druga zasada termodynamiki.

Termodynamiczna definicja entropii

Pojęcie entropii zostało po raz pierwszy wprowadzone w 1865 roku przez Rudolfa Clausiusa. Zdefiniował zmiana entropii układ termodynamiczny w proces odwracalny jako stosunek zmiany całkowitej ilości ciepła do wartości temperatury bezwzględnej:

Ten wzór ma zastosowanie tylko do procesu izotermicznego (zachodzącego w stałej temperaturze). Jego uogólnienie na przypadek dowolnego procesu quasi-statycznego wygląda następująco:

gdzie jest przyrostem (różniczką) entropii i jest nieskończenie małym przyrostem ilości ciepła.

Należy zwrócić uwagę, że rozważana definicja termodynamiczna ma zastosowanie tylko do procesów quasi-statycznych (składających się z następujących po sobie w sposób ciągły stanów równowagi).

Statystyczna definicja entropii: zasada Boltzmanna

W 1877 roku Ludwig Boltzmann odkrył, że entropia układu może odnosić się do liczby możliwych „mikrostanów” (stanów mikroskopowych) zgodnych z ich właściwościami termodynamicznymi. Rozważmy na przykład gaz doskonały w naczyniu. Mikrostan definiuje się jako pozycje i impulsy (momenty ruchu) każdego atomu tworzącego układ. Spójność wymaga od nas rozważenia tylko tych mikrostanów, dla których: (I) położenie wszystkich części znajduje się w naczyniu, (II) aby uzyskać całkowitą energię gazu, sumuje się energie kinetyczne atomów. Boltzmann postulował, że:

gdzie teraz znamy stałą 1,38 10 −23 J / K jako stałą Boltzmanna i jest to liczba mikrostanów, które są możliwe w istniejącym stanie makroskopowym (waga statystyczna stanu).

Druga zasada termodynamiki- zasada fizyczna, która nakłada ograniczenie na kierunek procesów wymiany ciepła między ciałami.

Druga zasada termodynamiki mówi, że samorzutne przekazanie ciepła z ciała mniej nagrzanego do ciała nagrzanego jest niemożliwe.

Bilet 6.

1. § 2.5. Twierdzenie o ruchu środka masy

Zależność (16) jest bardzo podobna do równania ruchu punktu materialnego. Spróbujmy sprowadzić to do jeszcze prostszej formy F=m A. Aby to zrobić, przekształcamy lewą stronę, korzystając z właściwości operacji różniczkowania (y+z) =y +z , (ay) =ay , a=const:

(24)

Pomnóż i podziel (24) przez masę całego układu i wstaw do równania (16):

. (25)

Wyrażenie w nawiasach ma wymiar długości i określa wektor promienia pewnego punktu, który nazywa się środek masy układu:

. (26)

W rzutach na osie współrzędnych (26) przyjmuje postać

(27)

Jeśli (26) podstawimy do (25), to otrzymamy twierdzenie o ruchu środka masy:

te. środek masy układu porusza się jako punkt materialny, w którym skupiona jest cała masa układu, pod działaniem sumy sił zewnętrznych przyłożonych do układu. Twierdzenie o ruchu środka masy mówi, że bez względu na to, jak złożone są siły oddziaływania cząstek układu między sobą i z ciałami zewnętrznymi, i bez względu na to, jak trudno poruszają się te cząstki, zawsze można znaleźć punkt (środek masy), którego ruch jest opisany w prosty sposób. Środek masy jest pewnym punktem geometrycznym, którego położenie jest określone przez rozkład mas w układzie i który nie może pokrywać się z żadną z jego materialnych cząstek.

Iloczyn masy układu i prędkości w cm jego środka masy, jak wynika z jego definicji (26), jest równe pędowi układu:

(29)

W szczególności, jeśli suma sił zewnętrznych jest równa zeru, to środek masy porusza się ruchem jednostajnym i prostoliniowym lub jest w spoczynku.

Środek masy będzie „latał” po tej samej trajektorii parabolicznej, po której poruszałby się niewybuch: jego przyspieszenie, zgodnie z (28), jest określone przez sumę wszystkich sił grawitacyjnych przyłożonych do odłamków i ich całkowitą masę, tj. to samo równanie, co ruch całego pocisku. Jednak gdy tylko pierwszy odłamek uderzy w Ziemię, siła reakcji Ziemi zostanie dodana do zewnętrznych sił grawitacji i ruch środka masy zostanie zniekształcony.

Ponieważ suma geometryczna sił zewnętrznych wynosi zero, przyspieszenie środka masy również wynosi zero i pozostanie on w spoczynku. Ciało będzie się obracać wokół stałego środka masy.

Czy prawo zachowania pędu ma jakąś przewagę nad prawami Newtona? Jaka jest moc tego prawa?

Jego główną zaletą jest to, że ma charakter integralny, tj. dotyczy charakterystyki układu (jego pędu) w dwóch stanach oddzielonych skończonym przedziałem czasu. Pozwala to na natychmiastowe uzyskanie ważnych informacji o stanie końcowym systemu, z pominięciem wszystkich jego stanów pośrednich i szczegółów zachodzących w tym przypadku interakcji.

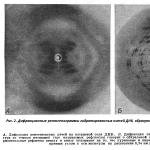
2) Prędkości cząsteczek gazu mają różne wartości i kierunki, a ze względu na ogromną liczbę zderzeń, jakich cząsteczka doświadcza w każdej sekundzie, jej prędkość stale się zmienia. Niemożliwe jest zatem określenie liczby cząsteczek, które mają dokładnie zadaną prędkość v w danym momencie czasu, ale możliwe jest policzenie liczby cząsteczek, których prędkości mają wartości leżące między pewnymi prędkościami v 1 i w 2 . Opierając się na teorii prawdopodobieństwa, Maxwell ustalił wzór, według którego można określić liczbę cząsteczek gazu, których prędkości w danej temperaturze mieszczą się w pewnym zakresie prędkości. Zgodnie z rozkładem Maxwella prawdopodobna liczba cząsteczek na jednostkę objętości; których składowe prędkości mieszczą się w przedziale od do, od do i od do, są określone przez rozkład Maxwella

gdzie m to masa cząsteczki, n to liczba cząsteczek na jednostkę objętości. Wynika z tego, że liczba cząsteczek, których prędkości bezwzględne leżą w przedziale od v do v + dv, ma postać

Rozkład Maxwella osiąga maksimum przy prędkości , tj. prędkość zbliżona do prędkości większości cząsteczek. Obszar zacienionego paska z podstawą dV pokaże, jaka część całkowitej liczby cząsteczek ma prędkości leżące w tym przedziale. Konkretna postać funkcji rozkładu Maxwella zależy od rodzaju gazu (masy cząsteczki) i temperatury. Ciśnienie i objętość gazu nie wpływają na rozkład cząsteczek przy prędkościach.

Krzywa rozkładu Maxwella pozwoli Ci znaleźć średnią arytmetyczną prędkości

Zatem,

Wraz ze wzrostem temperatury najbardziej prawdopodobna prędkość wzrasta, więc maksimum rozkładu cząsteczek pod względem prędkości przesuwa się w kierunku wyższych prędkości, a jej wartość bezwzględna maleje. W konsekwencji, gdy gaz jest ogrzewany, zmniejsza się udział cząsteczek o małych prędkościach, a zwiększa się udział cząsteczek o dużych prędkościach.

Dystrybucja Boltzmanna

Jest to rozkład energii cząstek (atomów, cząsteczek) gazu doskonałego w warunkach równowagi termodynamicznej. Rozkład Boltzmanna został odkryty w latach 1868-1871. australijski fizyk L. Boltzmann. Zgodnie z rozkładem liczba cząstek n i o całkowitej energii E i wynosi:

n i =A ω i e mi i /Kt (1)

gdzie ω i jest wagą statystyczną (liczbą możliwych stanów cząstki o energii e i). Stałą A wyznacza się z warunku, że suma n i po wszystkich możliwych wartościach i jest równa podanej całkowitej liczbie cząstek N w układzie (warunek normalizacji):

W przypadku, gdy ruch cząstek jest zgodny z mechaniką klasyczną, energię E i można uznać za składającą się z energii kinetycznej E ikin cząstki (cząsteczki lub atomu), jej energii wewnętrznej E iext (na przykład energia wzbudzenia elektronów ) i energia potencjalna E i , pot w polu zewnętrznym w zależności od położenia cząstki w przestrzeni:

mi i = mi, krewni + mi, ext + mi, pot (2)

Rozkład prędkości cząstek jest szczególnym przypadkiem rozkładu Boltzmanna. Występuje, gdy można pominąć wewnętrzną energię wzbudzenia

E i, ext oraz wpływ pól zewnętrznych E i, pot. Zgodnie z (2) wzór (1) można przedstawić jako iloczyn trzech wykładników, z których każdy daje rozkład cząstek na jeden rodzaj energii.

W stałym polu grawitacyjnym, które tworzy przyspieszenie g, dla cząstek gazów atmosferycznych w pobliżu powierzchni Ziemi (lub innych planet), energia potencjalna jest proporcjonalna do ich masy m i wysokości H nad powierzchnią, tj. Ei, pot = mgH. Po podstawieniu tej wartości do rozkładu Boltzmanna i zsumowaniu jej po wszystkich możliwych wartościach energii kinetycznej i wewnętrznej cząstek, otrzymuje się wzór barometryczny wyrażający prawo spadku gęstości atmosfery wraz z wysokością.

W astrofizyce, zwłaszcza w teorii widm gwiazd, rozkład Boltzmanna jest często używany do określenia względnej populacji elektronów na różnych poziomach energetycznych atomów. Jeżeli indeksami 1 i 2 oznaczymy dwa stany energetyczne atomu, to z rozkładu wynika:

n 2 / n 1 \u003d (ω 2 / ω 1) e - (E 2 - E 1) / kT (3) (wzór Boltzmanna).

Różnica energii E 2 -E 1 dla dwóch niższych poziomów energetycznych atomu wodoru wynosi >10 eV, a wartość kT, która charakteryzuje energię ruchu termicznego cząstek dla atmosfer gwiazd takich jak Słońce, wynosi tylko 0,3-1 eV. Dlatego wodór w takich gwiezdnych atmosferach jest w stanie niewzbudzonym. I tak w atmosferach gwiazd o temperaturze efektywnej Te > 5700 K (Słońce i inne gwiazdy) stosunek liczby atomów wodoru w stanie drugim i podstawowym wynosi 4,2 · 10 -9 .

Rozkład Boltzmanna uzyskano w ramach statystyki klasycznej. W latach 1924-26. powstała statystyka kwantowa. Doprowadziło to do odkrycia rozkładów Bosego-Einsteina (dla cząstek o spinie całkowitym) i Fermiego-Diraca (dla cząstek o spinie połówkowym). Oba te rozkłady przechodzą w rozkład, gdy średnia liczba stanów kwantowych dostępnych dla układu znacznie przekracza liczbę cząstek w układzie, tj. gdy na cząsteczkę przypada wiele stanów kwantowych, czyli innymi słowy, gdy stopień zajętości stanów kwantowych jest niewielki. Warunek stosowalności dla rozkładu Boltzmanna można zapisać jako nierówność:

gdzie N to liczba cząstek, V to objętość układu. Ta nierówność jest spełniona przy wysokiej temperaturze i małej liczbie cząstek na jednostkę. objętość (N/V). Wynika z tego, że im większa masa cząstek, tym szerszy zakres zmian T i N/V, obowiązuje rozkład Boltzmanna.

bilet 7.

Praca wszystkich przyłożonych sił jest równa pracy siły wypadkowej(patrz rys. 1.19.1).

Istnieje związek między zmianą prędkości ciała a pracą wykonaną przez siły przyłożone do ciała. Zależność tę najłatwiej ustalić, rozważając ruch ciała po linii prostej pod działaniem stałej siły.W tym przypadku wektory siły przemieszczenia, prędkości i przyspieszenia są skierowane wzdłuż jednej linii prostej, a ciało wykonuje ruch prostoliniowy jednostajnie przyspieszony. Kierując oś współrzędnych wzdłuż prostej linii ruchu, możemy rozważyć F, S, ty i A jako wielkości algebraiczne (dodatnie lub ujemne w zależności od kierunku odpowiedniego wektora). Wtedy pracę wykonaną przez siłę można zapisać jako A = fs. W ruchu jednostajnie przyspieszonym przemieszczenie S wyraża się wzorem

To wyrażenie pokazuje, że praca wykonana przez siłę (lub wypadkową wszystkich sił) jest związana ze zmianą kwadratu prędkości (a nie samej prędkości).

Nazywa się wielkość fizyczną równą połowie iloczynu masy ciała i kwadratu jego prędkości energia kinetyczna ciała:

To stwierdzenie nazywa się twierdzenie o energii kinetycznej . Twierdzenie o energii kinetycznej jest również ważne w ogólnym przypadku, gdy ciało porusza się pod działaniem zmieniającej się siły, której kierunek nie pokrywa się z kierunkiem ruchu.

Energia kinetyczna to energia ruchu. Energia kinetyczna ciała o masie M poruszanie się z prędkością jest równe pracy, jaką musi wykonać siła przyłożona do ciała w spoczynku, aby określić tę prędkość:

W fizyce obok energii kinetycznej czy energii ruchu pojęcie odgrywa ważną rolę energia potencjalna Lub energie oddziaływań ciał.

Energia potencjalna jest określona przez wzajemne położenie ciał (na przykład położenie ciała względem powierzchni Ziemi). Pojęcie energii potencjalnej można wprowadzić tylko dla sił, których praca nie zależy od trajektorii ruchu i jest określona jedynie przez początkowe i końcowe położenie ciała. Siły takie nazywamy konserwatywny .

Praca sił konserwatywnych na zamkniętej trajektorii wynosi zero. To stwierdzenie jest zilustrowane na ryc. 1.19.2.

Własność konserwatyzmu posiada siła grawitacji i siła sprężystości. Dla tych sił możemy wprowadzić pojęcie energii potencjalnej.

Jeśli ciało porusza się blisko powierzchni Ziemi, to działa na nie siła grawitacji, która jest stała co do wielkości i kierunku, a praca tej siły zależy tylko od pionowego ruchu ciała. Na dowolnym odcinku ścieżki pracę grawitacji można zapisać w rzutach wektora przemieszczenia na oś OJ skierowane pionowo w górę:

Praca ta jest równa zmianie pewnej wielkości fizycznej mgh wzięte z przeciwnym znakiem. Ta wielkość fizyczna nazywa się energia potencjalna ciała w polu grawitacji

Energia potencjalna mi p zależy od wyboru poziomu zerowego, czyli od wyboru początku osi OJ. To nie sama energia potencjalna ma znaczenie fizyczne, ale jej zmiana Δ mi p = mi p2 - mi p1 podczas przenoszenia ciała z jednej pozycji do drugiej. Zmiana ta nie zależy od wyboru poziomu zerowego.

Jeśli weźmiemy pod uwagę ruch ciał w polu grawitacyjnym Ziemi w znacznych odległościach od niego, to przy określaniu energii potencjalnej należy wziąć pod uwagę zależność siły grawitacji od odległości do środka Ziemi ( prawo grawitacji). W przypadku sił powszechnego ciążenia wygodnie jest policzyć energię potencjalną z nieskończenie odległego punktu, tj. Założyć, że energia potencjalna ciała w nieskończenie odległym punkcie jest równa zeru. Wzór wyrażający energię potencjalną ciała o masie M na odległość R od środka Ziemi ma postać ( patrz §1.24):

Gdzie M to masa ziemi, G jest stałą grawitacji.

Pojęcie energii potencjalnej można również wprowadzić dla siły sprężystości. Siła ta ma również właściwość bycia konserwatywnym. Rozciągając (lub ściskając) sprężynę, możemy to zrobić na różne sposoby.

Możesz po prostu wydłużyć sprężynę o pewną kwotę X lub najpierw wydłuż go o 2 X, a następnie zredukuj wydłużenie do wartości X itd. We wszystkich tych przypadkach siła sprężystości wykonuje tę samą pracę, która zależy tylko od wydłużenia sprężyny X w stanie końcowym, jeśli sprężyna była początkowo nieodkształcona. Praca ta jest równa pracy siły zewnętrznej A, wzięte ze znakiem przeciwnym ( patrz §1.18):

Energia potencjalna ciała odkształconego elastycznie jest równa pracy siły sprężystej podczas przejścia z danego stanu do stanu o zerowym odkształceniu.

Jeżeli w stanie początkowym sprężyna była już odkształcona, a jej wydłużenie było równe X 1, następnie po przejściu do nowego stanu z wydłużeniem X 2, siła sprężystości wykona pracę równą zmianie energii potencjalnej, wziętej ze znakiem przeciwnym:

W wielu przypadkach wygodnie jest użyć molowej pojemności cieplnej C:

gdzie M jest masą molową substancji.

W ten sposób wyznaczono pojemność cieplną nie jest jednoznaczna charakterystyka substancji. Zgodnie z pierwszą zasadą termodynamiki zmiana energii wewnętrznej ciała zależy nie tylko od ilości otrzymanego ciepła, ale także od pracy wykonanej przez ciało. W zależności od warunków, w jakich prowadzony był proces wymiany ciepła, ciało mogło wykonywać różną pracę. Dlatego ta sama ilość ciepła przekazana ciału może powodować różne zmiany jego energii wewnętrznej, a co za tym idzie temperatury.

Taka niejednoznaczność w określaniu pojemności cieplnej jest typowa tylko dla substancji gazowej. Gdy ciała ciekłe i stałe są podgrzewane, ich objętość praktycznie się nie zmienia, a praca ekspansji okazuje się równa zeru. Dlatego cała ilość ciepła otrzymanego przez ciało idzie na zmianę jego energii wewnętrznej. W przeciwieństwie do cieczy i ciał stałych, gaz w procesie wymiany ciepła może znacznie zmienić swoją objętość i wykonać pracę. Dlatego pojemność cieplna substancji gazowej zależy od charakteru procesu termodynamicznego. Zwykle bierze się pod uwagę dwie wartości pojemności cieplnej gazów: C V to molowa pojemność cieplna w procesie izochorycznym (V = const), a C p to molowa pojemność cieplna w procesie izobarycznym (p = const).

W procesie przy stałej objętości gaz nie działa: A \u003d 0. Z pierwszej zasady termodynamiki dla 1 mola gazu wynika

gdzie ΔV jest zmianą objętości 1 mola gazu doskonałego, gdy jego temperatura zmienia się o ΔT. Oznacza to:

gdzie R jest uniwersalną stałą gazową. Dla p = stała

Zatem zależność wyrażająca zależność między molowymi pojemnościami cieplnymi C p i C V ma postać (wzór Mayera):

Molowa pojemność cieplna C p gazu w procesie o stałym ciśnieniu jest zawsze większa niż molowa pojemność cieplna C V w procesie o stałej objętości (ryc. 3.10.1).

W szczególności ten stosunek jest zawarty we wzorze dla procesu adiabatycznego (patrz §3.9).

Pomiędzy dwiema izotermami o temperaturach T 1 i T 2 na wykresie (p, V) możliwe są różne ścieżki przejścia. Ponieważ dla wszystkich takich przejść zmiana temperatury ΔT = T 2 - T 1 jest taka sama, zatem zmiana ΔU energii wewnętrznej jest taka sama. Jednak praca A wykonana w tym przypadku oraz ilość ciepła Q uzyskanego w wyniku wymiany ciepła będą różne dla różnych dróg przejścia. Wynika z tego, że gaz ma nieskończoną liczbę pojemności cieplnych. C p i C V to tylko szczególne (i bardzo ważne dla teorii gazów) wartości pojemności cieplnych.

Bilet 8.

1 Oczywiście położenie jednego, nawet „specjalnego” punktu nie opisuje do końca ruchu całego rozpatrywanego układu ciał, ale mimo to lepiej znać położenie przynajmniej jednego punktu, niż nie wiedzieć nic. Niemniej jednak rozważ zastosowanie praw Newtona do opisu obrotu bryły sztywnej wokół nieruchomej osie 1 . Zacznijmy od najprostszego przypadku: niech materialny punkt masy M przymocowany nieważkim sztywnym prętem o długości R do ustalonej osi OO / (Rys. 106).

Punkt materialny może poruszać się wokół osi, pozostając w stałej odległości od niego, dlatego jego trajektorią będzie okrąg wyśrodkowany na osi obrotu. Oczywiście ruch punktu jest zgodny z równaniem drugiego prawa Newtona

Jednak bezpośrednie zastosowanie tego równania nie jest uzasadnione: po pierwsze, punkt ma jeden stopień swobody, więc wygodnie jest użyć kąta obrotu jako jedynej współrzędnej, a nie dwóch współrzędnych kartezjańskich; po drugie, na rozpatrywany układ działają siły reakcji w osi obrotu, a bezpośrednio na punkt materialny – siła naciągu pręta. Znalezienie tych sił jest osobnym problemem, którego rozwiązanie jest zbędne do opisu obrotu. Dlatego sensowne jest otrzymanie na podstawie praw Newtona specjalnego równania opisującego bezpośrednio ruch obrotowy. Niech w pewnym momencie pewna siła działa na punkt materialny F, leżącego w płaszczyźnie prostopadłej do osi obrotu (ryc. 107).

W kinematycznym opisie ruchu krzywoliniowego całkowity wektor przyspieszenia a jest wygodnie rozkładany na dwie składowe, normalną A N, skierowany do osi obrotu i styczny A τ skierowany równolegle do wektora prędkości. Nie potrzebujemy wartości przyspieszenia normalnego, aby określić prawo ruchu. Oczywiście przyspieszenie to jest również spowodowane działaniem sił, z których jedną jest nieznana siła rozciągająca działająca na pręt. Zapiszmy równanie drugiego prawa w rzucie na kierunek styczny:

Należy zauważyć, że siła reakcji pręta nie jest uwzględniona w tym równaniu, ponieważ jest skierowana wzdłuż pręta i prostopadle do wybranego rzutu. Zmiana kąta obrotu φ bezpośrednio określona przez prędkość kątową

ω = ∆φ/∆t,

którego zmianę z kolei opisuje przyspieszenie kątowe

ε = ∆ω/∆t.

Przyspieszenie kątowe jest powiązane ze składową przyspieszenia stycznego za pomocą zależności

A τ = rε.

Podstawiając to wyrażenie do równania (1), otrzymujemy równanie odpowiednie do wyznaczenia przyspieszenia kątowego. Wygodnie jest wprowadzić nową wielkość fizyczną, która określa oddziaływanie ciał podczas ich obrotu. W tym celu mnożymy obie strony równania (1) przez R:

Pan 2 ε = F τ R. (2)

Rozważ wyrażenie po jego prawej stronie F τ R, co oznacza iloczyn stycznej składowej siły przez odległość od osi obrotu do punktu przyłożenia siły. Ta sama praca może być przedstawiona w nieco innej formie (ryc. 108):

M=F τ r = Frcosα = Fd,

Tutaj D jest odległością od osi obrotu do linii działania siły, która jest również nazywana ramieniem siły. Ta wielkość fizyczna jest iloczynem modułu siły i odległości od linii działania siły do ​​osi obrotu (ramię siły) M = Fd− nazywamy momentem siły. Działanie siły może skutkować obrotem zarówno w kierunku zgodnym z ruchem wskazówek zegara, jak i przeciwnym do ruchu wskazówek zegara. Zgodnie z wybranym dodatnim kierunkiem obrotu należy również wyznaczyć znak momentu siły. Należy zauważyć, że moment siły jest określony przez składową siły, która jest prostopadła do wektora promienia punktu przyłożenia. Składowa wektora siły skierowana wzdłuż odcinka łączącego punkt przyłożenia i oś obrotu nie prowadzi do rozkręcenia ciała. Składowa ta, gdy oś jest nieruchoma, jest kompensowana przez siłę reakcji w osi, dzięki czemu nie wpływa na obrót ciała. Zapiszmy jeszcze jedno przydatne wyrażenie na moment siły. Niech władza F przymocowany do punktu A, którego współrzędne kartezjańskie to X, Na(Rys. 109).

Rozłóżmy siłę F na dwa komponenty F X , F Na, równolegle do odpowiednich osi współrzędnych. Moment siły F wokół osi przechodzącej przez początek jest oczywiście równy sumie momentów składowych F X , F Na, to jest

M = xF Na − yF X .

Podobnie jak wprowadziliśmy pojęcie wektora prędkości kątowej, możemy również zdefiniować pojęcie wektora momentu siły. Moduł tego wektora odpowiada definicji podanej powyżej, ale jest skierowany prostopadle do płaszczyzny zawierającej wektor siły i odcinek łączący punkt przyłożenia siły z osią obrotu (rys. 110).

Wektor momentu siły można również zdefiniować jako iloczyn wektorowy wektora promienia punktu przyłożenia siły i wektora siły

Zauważ, że gdy punkt przyłożenia siły jest przesuwany wzdłuż linii jej działania, moment siły nie zmienia się. Oznaczmy iloczyn masy punktu materialnego przez kwadrat odległości do osi obrotu

Pan 2 = ja

(ta wartość nazywa się moment bezwładności punkt materialny wokół osi). Korzystając z tych zapisów, równanie (2) przybiera postać, która formalnie pokrywa się z równaniem drugiego prawa Newtona dla ruchu postępowego:

Iε = M. (3)

Równanie to nazywane jest podstawowym równaniem dynamiki ruchu obrotowego. Tak więc moment siły w ruchu obrotowym pełni taką samą rolę jak siła w ruchu postępowym - to on decyduje o zmianie prędkości kątowej. Okazuje się (i potwierdza to nasze codzienne doświadczenie), że o wpływie siły na prędkość obrotową decyduje nie tylko wielkość siły, ale także punkt jej przyłożenia. Moment bezwładności określa właściwości bezwładności ciała względem obrotu (w uproszczeniu pokazuje, czy łatwo jest obrócić ciało): im dalej od osi obrotu znajduje się punkt materialny, tym trudniej jest wpraw go w ruch obrotowy. Równanie (3) można uogólnić na przypadek obrotu dowolnego ciała. Kiedy ciało obraca się wokół ustalonej osi, przyspieszenia kątowe wszystkich punktów ciała są takie same. Dlatego, podobnie jak wyprowadzaliśmy równanie Newtona dla ruchu postępowego ciała, możemy napisać równania (3) dla wszystkich punktów obracającego się ciała, a następnie je zsumować. W rezultacie otrzymujemy równanie, które na zewnątrz pokrywa się z (3), w którym I- moment bezwładności całego ciała, równy sumie momentów jego punktów materialnych składowych, M jest sumą momentów sił zewnętrznych działających na ciało. Pokażmy, jak oblicza się moment bezwładności ciała. Należy podkreślić, że moment bezwładności ciała zależy nie tylko od masy, kształtu i wymiarów ciała, ale także od położenia i orientacji osi obrotu. Formalnie procedura obliczeniowa sprowadza się do podzielenia ciała na małe części, które można uznać za punkty materialne (ryc. 111),

oraz sumowanie momentów bezwładności tych punktów materialnych, które są równe iloczynowi masy przez kwadrat odległości do osi obrotu:

Dla ciał o prostym kształcie takie sumy są od dawna obliczane, więc często wystarczy zapamiętać (lub znaleźć w podręczniku) odpowiedni wzór na pożądany moment bezwładności. Jako przykład: moment bezwładności okrągłego jednorodnego walca, masy M i promień R, dla osi obrotu pokrywającej się z osią cylindra jest równa:

ja = (1/2)mR 2 (Ryc. 112).

W tym przypadku ograniczamy się do rozważenia obrotu wokół ustalonej osi, ponieważ opis dowolnego ruchu obrotowego ciała jest złożonym problemem matematycznym, wykraczającym daleko poza zakres lekcji matematyki w szkole średniej. Znajomość innych praw fizycznych, poza rozważanymi przez nas, tego opisu nie wymaga.

2 Energia wewnętrzna ciało (tzw mi Lub u) to całkowita energia tego ciała minus energia kinetyczna ciała jako całości i energia potencjalna ciała w zewnętrznym polu sił. W konsekwencji na energię wewnętrzną składa się energia kinetyczna chaotycznego ruchu cząsteczek, energia potencjalna interakcji między nimi oraz energia wewnątrzcząsteczkowa.

Energia wewnętrzna ciała to energia ruchu i interakcji cząstek tworzących ciało.

Energia wewnętrzna ciała to całkowita energia kinetyczna ruchu cząsteczek ciała i energia potencjalna ich interakcji.

Energia wewnętrzna jest jednowartościową funkcją stanu układu. Oznacza to, że ilekroć układ znajdzie się w danym stanie, jego energia wewnętrzna przyjmuje wartość właściwą temu stanowi, niezależnie od historii układu. W konsekwencji zmiana energii wewnętrznej podczas przejścia z jednego stanu do drugiego zawsze będzie równa różnicy wartości w tych stanach, niezależnie od ścieżki, po której nastąpiło przejście.

Energii wewnętrznej ciała nie można zmierzyć bezpośrednio. Można wyznaczyć tylko zmianę energii wewnętrznej:

Dla procesów quasi-statycznych zachodzi następująca zależność:

1. Informacje ogólne Ilość ciepła potrzebna do podniesienia temperatury o 1°C nazywa się pojemność cieplna i jest oznaczony literą Z. W obliczeniach technicznych pojemność cieplną mierzy się w kilodżulach. Podczas korzystania ze starego systemu jednostek pojemność cieplną wyraża się w kilokaloriach (GOST 8550-61) * W zależności od jednostek, w których mierzona jest ilość gazu, rozróżnia się: molową pojemność cieplną \xc na kJ/(kmol x X grad); masowa pojemność cieplna c kJ/(kg-stopnie); objętościowa pojemność cieplna Z V kJ/(m 3 grad). Przy określaniu objętościowej pojemności cieplnej należy wskazać, do jakich wartości temperatury i ciśnienia ona się odnosi. Zwyczajowo określa się objętościową pojemność cieplną w normalnych warunkach fizycznych.Pojemność cieplna gazów podlegających prawom gazu doskonałego zależy tylko od temperatury.Istnieją średnie i rzeczywiste pojemności cieplne gazów. Rzeczywista pojemność cieplna to stosunek nieskończenie małej ilości dostarczonego ciepła Dd do wzrostu temperatury o nieskończenie małą ilość Na:Średnia pojemność cieplna określa średnią ilość dostarczonego ciepła, gdy jednostkowa ilość gazu jest podgrzewana o 1 ° w zakresie temperatur od T X zanim T%: Gdzie Q- ilość ciepła dostarczonego do masy jednostkowej gazu, gdy jest on podgrzewany z temperatury T T do temperatury T%. W zależności od charakteru procesu, w którym ciepło jest dostarczane lub odbierane, wartość pojemności cieplnej gazu będzie różna.Jeżeli gaz jest ogrzewany w naczyniu o stałej objętości (V\u003d "\u003d const), wtedy ciepło jest zużywane tylko w celu zwiększenia jego temperatury. Jeśli gaz znajduje się w cylindrze z ruchomym tłokiem, to po dostarczeniu ciepła ciśnienie gazu pozostaje stałe (p == stała). Jednocześnie gaz po podgrzaniu rozszerza się i wykonuje pracę przeciwko siłom zewnętrznym, jednocześnie zwiększając swoją temperaturę. Aby uzyskać różnicę między temperaturą końcową i początkową podczas ogrzewania gazu w procesie R= const byłoby takie samo jak w przypadku ogrzewania o godz V= = const, ilość wydatkowanego ciepła musi być większa o ilość równą pracy wykonanej przez gaz w procesie p == konst. Wynika z tego, że pojemność cieplna gazu przy stałym ciśnieniu Z R będzie większa niż pojemność cieplna przy stałej objętości.Drugi człon w równaniach charakteryzuje ilość ciepła zużywanego na działanie gazu w procesie R= = const, gdy temperatura zmienia się o 1° Przeprowadzając przybliżone obliczenia, można przyjąć, że pojemność cieplna ciała roboczego jest stała i nie zależy od temperatury. W tym przypadku znajomość molowych pojemności cieplnych przy stałej objętości można przyjąć odpowiednio dla gazów jedno-, dwu- i wieloatomowych równych 12,6; 20,9 i 29,3 kJ/(kmol-deg) lub 3; 5 i 7 kcal/(kmol-deg).