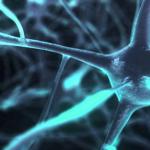
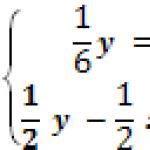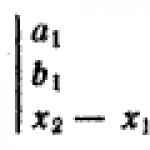Wibracje swobodne powstają pod działaniem sił wewnętrznych układu po wytrąceniu układu z równowagi.
W celu drgania swobodne zostały wykonane zgodnie z prawem harmonicznym, konieczne jest, aby siła dążąca do powrotu ciała do położenia równowagi była proporcjonalna do wychylenia ciała z położenia równowagi i skierowana w kierunku przeciwnym do przemieszczenia (patrz § 2.1):
Nazywa się siły o dowolnej innej naturze fizycznej, które spełniają ten warunek quasi-elastyczny .
Zatem ładunek o pewnej masie M przymocowana do sprężyny usztywniającej k, którego drugi koniec jest nieruchomy (ryc. 2.2.1), stanowią układ zdolny do wykonywania swobodnych oscylacji harmonicznych przy braku tarcia. Nazywa się msza na wiosnę harmoniczna liniowa oscylator.
Częstotliwość kołową ω 0 drgań własnych obciążenia sprężyny wyznacza drugie prawo dynamiki Newtona:
Przy poziomym układzie układu sprężynowego siła grawitacji przyłożona do ładunku jest kompensowana przez siłę reakcji podpory. Jeśli ładunek jest zawieszony na sprężynie, wówczas siła grawitacji jest skierowana wzdłuż linii ruchu ładunku. W położeniu równowagi sprężyna jest rozciągnięta o pewną wartość X 0 równe
Dlatego drugie prawo Newtona dotyczące obciążenia sprężyny można zapisać jako
Równanie (*) jest wywoływane równanie drgań swobodnych . Należy zauważyć, że właściwości fizyczne układu oscylacyjnego wyznaczyć tylko częstotliwość drgań własnych ω 0 lub okres T . Takie parametry procesu oscylacyjnego jak amplituda X m i faza początkowa φ 0 są określone przez sposób, w jaki układ został wyprowadzony z równowagi w początkowej chwili czasu.
Jeśli, na przykład, ładunek został przesunięty z położenia równowagi o odległość Δ l a potem w czasie T= 0 zwolniony bez prędkości początkowej, a następnie X m = ∆ l, φ 0 = 0.
Jeżeli jednak początkowa prędkość ± υ 0 została nadana ładunkowi, który znajdował się w położeniu równowagi, za pomocą gwałtownego pchnięcia, to
A więc amplituda X wyznaczane są oscylacje swobodne m i jego faza początkowa φ 0 warunki początkowe .
Istnieje wiele odmian mechanicznych układów oscylacyjnych, które wykorzystują siły odkształceń sprężystych. na ryc. 2.2.2 przedstawia analog kątowy liniowego oscylatora harmonicznego. Poziomo umieszczony krążek wisi na elastycznej nici zamocowanej w jego środku masy. Kiedy dysk obraca się o kąt θ, powstaje moment sił M sprężyste odkształcenie skrętne:
Gdzie I = I C - moment bezwładności dysku względem osi przechodzącej przez środek masy, ε - przyspieszenie kątowe.
Analogicznie do obciążenia sprężyny można uzyskać:
Wibracje swobodne. Wahadło matematyczne
Wahadło matematyczne zwane ciałem o niewielkich rozmiarach, zawieszonym na cienkiej nierozciągliwej nici, którego masa jest znikoma w porównaniu z masą ciała. W pozycji równowagi, gdy wahadło wisi na pionie, siła grawitacji równoważy się siłą naprężenia nici. Kiedy wahadło odchyla się od położenia równowagi o pewien kąt φ, pojawia się styczna składowa grawitacji F τ = - mg grzech φ (ryc. 2.3.1). Znak minus w tym wzorze oznacza, że składowa styczna jest skierowana w kierunku przeciwnym do wychylenia wahadła.
Jeśli oznaczony przez X liniowe przemieszczenie wahadła z położenia równowagi wzdłuż łuku koła o promieniu l, to jego przemieszczenie kątowe będzie równe φ = X / l. Drugie prawo Newtona, zapisane dla rzutów wektorów przyspieszenia i siły na kierunek stycznej, daje:
Ta zależność pokazuje, że wahadło matematyczne jest złożone nieliniowy układu, ponieważ siła zmierzająca do przywrócenia wahadła do położenia równowagi jest proporcjonalna do braku przemieszczenia X, A
Tylko na wszelki wypadek małe fluktuacje kiedy blisko można zastąpić wahadłem matematycznym, jest oscylatorem harmonicznym, tj. układem zdolnym do wykonywania oscylacji harmonicznych. W praktyce przybliżenie to obowiązuje dla kątów rzędu 15-20°; natomiast wartość różni się od nie więcej niż 2%. Oscylacje wahadła przy dużych amplitudach nie są harmoniczne.
Dla małych oscylacji wahadła matematycznego drugie prawo Newtona jest zapisane jako
Ta formuła wyraża częstotliwość drgań własnych wahadła matematycznego .
Stąd,
|
Każde ciało zamontowane na poziomej osi obrotu może wykonywać swobodne oscylacje w polu grawitacyjnym, a zatem jest również wahadłem. Takie wahadło nazywa się fizyczny (Rys. 2.3.2). Różni się od matematycznego jedynie rozkładem mas. W położeniu stabilnej równowagi środek masy C wahadła fizycznego znajduje się poniżej osi obrotu O na pionie przechodzącym przez tę oś. Gdy wahadło wychyla się o kąt φ, powstaje moment ciężkości, dążący do przywrócenia wahadła do położenia równowagi:
a drugie prawo Newtona dla wahadła fizycznego staje się (patrz §1.23)
Tutaj ω 0 - naturalna częstotliwość małych oscylacji wahadła fizycznego .
Stąd,
Dlatego równanie wyrażające drugie prawo Newtona dla wahadła fizycznego można zapisać jako
Ostatecznie dla częstotliwości kołowej ω 0 drgań swobodnych wahadła fizycznego otrzymujemy wyrażenie:
|
Przemiany energii podczas swobodnych drgań mechanicznych
Przy swobodnych drganiach mechanicznych energia kinetyczna i potencjalna zmieniają się okresowo. Przy maksymalnym odchyleniu ciała od położenia równowagi jego prędkość, a co za tym idzie energia kinetyczna, zanika. W tej pozycji energia potencjalna ciała oscylującego osiąga swoją maksymalną wartość. W przypadku obciążenia sprężyny energia potencjalna jest energią sprężystego odkształcenia sprężyny. W przypadku wahadła matematycznego jest to energia pola grawitacyjnego Ziemi.
Kiedy ciało w swoim ruchu przechodzi przez położenie równowagi, jego prędkość jest maksymalna. Ciało pomija położenie równowagi zgodnie z prawem bezwładności. W tym momencie ma maksymalną energię kinetyczną i minimalną energię potencjalną. Wzrost energii kinetycznej następuje kosztem spadku energii potencjalnej. Przy dalszym ruchu energia potencjalna zaczyna rosnąć z powodu spadku energii kinetycznej itp.
Tak więc podczas oscylacji harmonicznych następuje okresowa przemiana energii kinetycznej w energię potencjalną i odwrotnie.
Jeśli w układzie oscylacyjnym nie ma tarcia, to całkowita energia mechaniczna podczas drgań swobodnych pozostaje niezmieniona.
Do obciążenia sprężyny(patrz §2.2):
W rzeczywistych warunkach na każdy układ oscylacyjny działają siły tarcia (opór). W tym przypadku część energii mechanicznej jest zamieniana na energię wewnętrzną ruchu termicznego atomów i cząsteczek, a drgania stają się zblakły (Rys. 2.4.2).
Szybkość tłumienia oscylacji zależy od wielkości sił tarcia. Przedział czasu τ, w którym amplituda oscylacji maleje mi≈ 2,7 razy, tzw czas rozpadu .
Częstotliwość oscylacji swobodnych zależy od szybkości tłumienia oscylacji. Wraz ze wzrostem sił tarcia częstotliwość drgań własnych maleje. Jednak zmiana częstotliwości drgań własnych staje się zauważalna dopiero przy odpowiednio dużych siłach tarcia, gdy drgania własne szybko zanikają.
Ważną cechą układu oscylacyjnego, który wykonuje oscylacje z tłumieniem swobodnym, jest współczynnik jakości Q. Ten parametr jest zdefiniowany jako liczba N suma oscylacji wykonanych przez układ w czasie tłumienia τ pomnożona przez π:
Zatem współczynnik jakości charakteryzuje względną utratę energii układu oscylacyjnego z powodu obecności tarcia w przedziale czasu równym jednemu okresowi oscylacji.
Wibracje wymuszone. Rezonans. Samooscylacje
Nazywa się oscylacje, które występują pod wpływem zewnętrznej siły okresowej wymuszony.
Siła zewnętrzna wykonuje dodatnią pracę i zapewnia dopływ energii do układu oscylacyjnego. Nie pozwala na zanik oscylacji pomimo działania sił tarcia.
Okresowa siła zewnętrzna może zmieniać się w czasie zgodnie z różnymi prawami. Szczególnie interesujący jest przypadek, gdy siła zewnętrzna, zmieniająca się zgodnie z prawem harmonicznym z częstotliwością ω, działa na układ oscylacyjny zdolny do wykonywania drgań własnych z określoną częstotliwością ω 0 .
Jeżeli swobodne oscylacje występują z częstotliwością ω 0, która jest określona przez parametry układu, to stałe wymuszone oscylacje zawsze występują przy częstotliwość ω siły zewnętrznej.
Po rozpoczęciu oddziaływania siły zewnętrznej na układ oscylacyjny, po pewnym czasie Δ T ustanowić wymuszone oscylacje. Czas ustalania się jest równy rządowi wielkości czasowi zaniku τ oscylacji swobodnych w układzie oscylacyjnym.
W chwili początkowej w układzie oscylacyjnym wzbudzone są oba procesy - oscylacje wymuszone o częstotliwości ω i oscylacje swobodne o częstotliwości własnej ω 0 . Ale drgania swobodne są tłumione z powodu nieuniknionej obecności sił tarcia. Dlatego po pewnym czasie w układzie oscylacyjnym pozostają tylko drgania stacjonarne o częstotliwości ω zewnętrznej siły napędowej.
Rozważmy jako przykład drgania wymuszone ciała na sprężynie (rys. 2.5.1). Na wolny koniec sprężyny działa siła zewnętrzna. Wymusza to swobodny (lewy na ryc. 2.5.1) koniec sprężyny, aby poruszał się zgodnie z prawem
Jeśli lewy koniec sprężyny zostanie przesunięty o odległość y, a prawy - na odległość X od ich pierwotnego położenia, gdy sprężyna nie była odkształcona, to wydłużenie sprężyny Δ l równa się:
W tym równaniu siła działająca na ciało jest reprezentowana przez dwa wyrazy. Pierwszy człon po prawej stronie to siła sprężystości dążąca do przywrócenia ciała do położenia równowagi ( X= 0). Drugi termin to zewnętrzne okresowe oddziaływanie na organizm. Ten termin to tzw przekonująca siła.
Równaniu wyrażającemu drugie prawo Newtona dla ciała na sprężynie w obecności zewnętrznego działania okresowego można nadać ścisłą postać matematyczną, jeśli weźmiemy pod uwagę zależność między przyspieszeniem ciała a jego współrzędną: Wtedy zostanie zapisane w formularzu
Równanie (**) nie uwzględnia działania sił tarcia. w odróżnieniu równania drgań swobodnych(*) (patrz §2.2) równanie drgań wymuszonych(**) zawiera dwie częstotliwości – częstotliwość drgań swobodnych ω 0 oraz częstotliwość ω siły napędowej.
Stałe wymuszone drgania obciążenia sprężyny występują z częstotliwością działania zewnętrznego zgodnie z prawem
|
Amplituda drgań wymuszonych X m i faza początkowa θ zależą od stosunku częstotliwości ω 0 i ω oraz od amplitudy y m siła zewnętrzna.
Przy bardzo niskich częstotliwościach, gdy ω<< ω 0 , движение тела массой M, przymocowany do prawego końca sprężyny, powtarza ruch lewego końca sprężyny. W której X(T) = y(T), a sprężyna pozostaje praktycznie nieodkształcona. Siła zewnętrzna przyłożona do lewego końca sprężyny nie działa, ponieważ moduł tej siły wynosi ω<< ω 0 стремится к нулю.
Jeśli częstotliwość ω siły zewnętrznej zbliża się do częstotliwości własnej ω 0 , następuje gwałtowny wzrost amplitudy oscylacji wymuszonych. Zjawisko to nazywa się rezonans . Zależność od amplitudy X m oscylacje wymuszone od częstotliwości ω siły napędowej nazywamy charakterystyka rezonansowa Lub krzywa rezonansowa(Rys. 2.5.2).
W rezonansie amplituda X m fluktuacje obciążenia mogą być wielokrotnie większe niż amplituda y m drgania wolnego (lewego) końca sprężyny spowodowane działaniem zewnętrznym. W przypadku braku tarcia amplituda drgań wymuszonych w rezonansie powinna rosnąć w nieskończoność. W warunkach rzeczywistych amplitudę drgań wymuszonych w stanie ustalonym określa warunek: praca siły zewnętrznej w okresie drgań musi być równa utracie energii mechanicznej w tym samym czasie na skutek tarcia. Im mniejsze tarcie (tj. wyższy współczynnik jakości Q układ oscylacyjny), tym większa amplituda oscylacji wymuszonych w rezonansie.
Dla układów oscylacyjnych o niezbyt wysokim współczynniku jakości (< 10) резонансная частота несколько смещается в сторону низких частот. Это хорошо заметно на рис. 2.5.2.
Zjawisko rezonansu może powodować niszczenie mostów, budynków i innych konstrukcji, jeśli częstotliwości drgań własnych ich drgań pokrywają się z częstotliwością okresowo działającej siły, która powstała np. w wyniku obracania się niezrównoważonego silnika.
Wibracje wymuszone są nietłumiony fluktuacje. Nieuchronne straty energii spowodowane tarciem są kompensowane przez dostarczanie energii z zewnętrznego źródła okresowo działającej siły. Istnieją układy, w których oscylacje nietłumione powstają nie w wyniku okresowych wpływów zewnętrznych, ale w wyniku zdolności takich układów do regulowania przepływu energii ze stałego źródła. Takie systemy to tzw samooscylujące, oraz proces oscylacji nietłumionych w takich układach - samooscylacje . W układzie samooscylacyjnym można wyróżnić trzy charakterystyczne elementy – układ oscylacyjny, źródło energii oraz urządzenie sprzężenia zwrotnego pomiędzy układem oscylacyjnym a źródłem. Jako układ oscylacyjny można zastosować dowolny układ mechaniczny zdolny do wykonywania własnych tłumionych oscylacji (na przykład wahadło zegara ściennego).
Źródłem energii może być energia odkształcenia sprężyny lub energia potencjalna obciążenia w polu grawitacyjnym. Urządzenie sprzężenia zwrotnego to mechanizm, za pomocą którego system samooscylacyjny reguluje przepływ energii ze źródła. na ryc. 2.5.3 pokazuje schemat interakcji różnych elementów układu samooscylacyjnego.
Przykładem mechanicznego systemu samooscylacyjnego jest mechanizm zegarowy kotwica poruszać się (ryc. 2.5.4). Koło jezdne o skośnych zębach jest sztywno przymocowane do zębatego bębna, przez który przerzucany jest łańcuch z obciążnikiem. Mocowany do górnego końca wahadła kotwica(kotwica) z dwoma płytkami z twardego materiału, zakrzywionymi wzdłuż łuku koła ze środkiem na osi wahadła. W zegarku naręcznym ciężarek zastąpiono sprężyną, a wahadło balanserem - pokrętłem przymocowanym do spiralnej sprężyny. Wyważarka wykonuje drgania skrętne wokół własnej osi. Układ oscylacyjny w zegarze to wahadło lub balanser.
Źródłem energii jest podniesiony ciężarek lub nawinięta sprężyna. Urządzenie sprzężenia zwrotnego to kotwica, która umożliwia obracanie koła jezdnego o jeden ząb w jednym pół cyklu. Sprzężenie zwrotne zapewnia interakcja kotwicy z kołem jezdnym. Przy każdym ruchu wahadła ząb koła jezdnego popycha widełki kotwicy w kierunku ruchu wahadła, przekazując mu pewną porcję energii, która kompensuje straty energii na skutek tarcia. W ten sposób energia potencjalna ciężarka (lub skręconej sprężyny) jest stopniowo, w oddzielnych porcjach, przenoszona na wahadło.
Mechaniczne układy samooscylacyjne są szeroko rozpowszechnione w otaczającym nas życiu iw technice. Samooscylacje wykonują silniki parowe, silniki spalinowe, dzwonki elektryczne, struny smyczkowych instrumentów muzycznych, kolumny powietrza w rurach instrumentów dętych, struny głosowe podczas mówienia lub śpiewania itp.
 |
| Rysunek 2.5.4. Mechanizm zegara z wahadłem. |
Kandydat nauk fizycznych i matematycznych V. POGOZHEV.
(Koniec. Początek, patrz nr „Nauka i życie”)
Publikujemy ostatnią część zadań na temat „Mechanika”. Następny artykuł będzie poświęcony oscylacjom i falom.
Zadanie 4 (1994). Ze wzgórza, płynnie przechodząc w płaszczyznę poziomą, z wysokości H zsuwa się z małej gładkiej podkładki masy M. Na płaszczyźnie znajduje się gładkie ruchome wzniesienie masy M i wysokość H> H. Przekroje suwaków płaszczyzną pionową przechodzącą przez środki mas podkładki i suwaka ruchomego mają postać pokazaną na rysunku. Jaka jest maksymalna wysokość X Czy krążek może wejść na stałą zjeżdżalnię po pierwszym ześlizgnięciu się z ruchomej zjeżdżalni?
Rozwiązanie. Zjeżdżalnia, na której pierwotnie znajdował się krążek, jest nieruchoma ze względu na stan problemu i dlatego jest sztywno przymocowana do Ziemi. Jeśli, jak to zwykle bywa przy rozwiązywaniu takich problemów, uwzględnione zostaną tylko siły interakcji krążka ze zjeżdżalniami i siła grawitacji, problem można rozwiązać, korzystając z praw zachowania energii mechanicznej i pędu. Laboratoryjny układ odniesienia, jak już zauważono w rozwiązaniu poprzednich problemów (patrz „Nauka i życie” nr ), można uznać za inercyjny. Rozwiązanie problemu podzielimy na trzy etapy. W pierwszym etapie krążek zaczyna zjeżdżać ze zjeżdżalni stałej, w drugim wchodzi w interakcję ze zjeżdżalnią ruchomą, aw ostatnim etapie wznosi się po zjeżdżalni stałej. Z warunków zadania i przyjętych założeń wynika, że krążek i ruchoma ślizgawka mogą poruszać się tylko do przodu, tak aby ich środki ciężkości pozostawały cały czas w tej samej płaszczyźnie pionowej.
Biorąc pod uwagę powyższe oraz fakt, że krążek jest gładki, system „Ziemia ze stałą górką – krążek” w pierwszym etapie należy uznać za odosobniony i konserwatywny. Dlatego, zgodnie z prawem zachowania energii mechanicznej, energia kinetyczna krążka W k = mv 1 2 /2 gdy porusza się po płaszczyźnie poziomej po zjechaniu z górki powinno być równe mgh, Gdzie G- wielkość przyspieszenia swobodnego spadania.
W drugim etapie krążek najpierw zacznie się unosić po ruchomej zjeżdżalni, a następnie po osiągnięciu określonej wysokości zjedzie z niej. Stwierdzenie to wynika z faktu, że w wyniku oddziaływania krążka z ruchomą ślizgawką, ta ostatnia, jak już wspomniano, pod koniec drugiego etapu powinna posunąć się do przodu z określoną prędkością u, oddalając się od ustalonego slajdu, czyli w kierunku prędkości w 1 krążek na koniec pierwszego etapu. Dlatego nawet gdyby wysokość ruchomej zjeżdżalni była równa H, krążek nie byłby w stanie go pokonać. Biorąc pod uwagę, że siła reakcji od strony płaszczyzny poziomej na ruchomą zjeżdżalnię oraz siły grawitacyjne działające na tę zjeżdżalnię i krążek skierowane są pionowo, w oparciu o prawo zachowania pędu, można stwierdzić, że występ w 2 prędkości krążka na końcu drugiego etapu na kierunek prędkości w 1 krążek na koniec pierwszego etapu musi spełniać równanie
mυ 1 = mυ 2 + M I (1)
Z drugiej strony, zgodnie z zasadą zachowania energii mechanicznej, prędkości te są powiązane zależnością
![]() , (2)
, (2)
gdyż układ „Ziemia – ruchoma zjeżdżalnia – krążek” okazuje się przy przyjętych założeniach izolowany konserwatywnie, a jego energia potencjalna na początku i na końcu drugiego etapu jest taka sama. Biorąc pod uwagę, że po interakcji z ruchomą zjeżdżalnią prędkość krążka w ogólnym przypadku powinna ulec zmianie ( w 1 - w 2 ≠ 0), a korzystając ze wzoru na różnicę kwadratów dwóch wielkości, z zależności (1) i (2) otrzymujemy
υ 1 + υ 2 = I (3)
a następnie z (3) i (1) wyznaczamy rzut prędkości krążka pod koniec drugiego etapu na kierunek jego prędkości przed rozpoczęciem interakcji z poruszającym się suwakiem
Z zależności (4) wynika, że w 1 ≠ w 2 godz M≠ M a krążek przesunie się w kierunku stałego wzgórza po zjechaniu z ruchomego tylko wtedy, gdy M< M.
Stosując ponownie zasadę zachowania energii mechanicznej dla układu „Ziemia ze stałym wzniesieniem - krążek”, wyznaczamy maksymalną wysokość podnoszenia krążka po stałym wzniesieniu X =w 2 2 /2G. Po najprostszych przekształceniach algebraicznych ostateczną odpowiedź można przedstawić jako

Zadanie 5(1996). Gładki blok masy M mocowana do pionowej ściany za pomocą lekkiej sprężyny usztywniającej k. Przy nieodkształconej sprężynie koniec pręta dotyka powierzchni sześcianu, czyli masy M czyli dużo mniej M. Oś sprężyny jest pozioma i leży w płaszczyźnie pionowej przechodzącej przez środki masy sześcianu i pręta. Przesunięcie pręta powoduje ściśnięcie sprężyny wzdłuż jej osi o wartość ∆ X, po czym blok jest zwalniany bez prędkości początkowej. Jak daleko przesunie się sześcian po zderzeniu doskonale sprężystym, jeśli współczynnik tarcia sześcianu po płaszczyźnie jest wystarczająco mały i równy μ?
Rozwiązanie. Przyjmiemy, że standardowe założenia są spełnione: laboratoryjny układ odniesienia, względem którego wszystkie ciała początkowo spoczywały, jest inercjalny i na rozważane ciała działają tylko siły wzajemnego oddziaływania między nimi i grawitacji, a dodatkowo , płaszczyzna styku pręta z sześcianem jest prostopadła do osi sprężyny. Następnie, biorąc pod uwagę położenie osi sprężyny oraz środki masy pręta i sześcianu podane w warunku, możemy przyjąć, że ciała te mogą poruszać się tylko do przodu.
Po zwolnieniu sztanga zaczyna się poruszać pod działaniem ściśniętej sprężyny. W momencie, gdy pręt dotyka sześcianu, w zależności od stanu problemu, sprężyna powinna stać się nieodkształcona. Ponieważ klocek jest gładki i porusza się wzdłuż płaszczyzny poziomej, siły grawitacji i reakcje płaszczyzny nie działają na nim. W zależności od warunku masę sprężyny (a tym samym energię kinetyczną jej ruchomych części) można pominąć. W konsekwencji energia kinetyczna poruszającego się postępowo pręta w momencie zetknięcia się sześcianu powinna zrównać się z energią potencjalną sprężyny w momencie zwolnienia pręta, a zatem prędkość pręta w tym momencie powinna być równa .
Kiedy pasek dotyka sześcianu, zderzają się. W tym przypadku siła tarcia działająca na sześcian zmienia się od zera do m mg, Gdzie G- wielkość przyspieszenia swobodnego spadania. Zakładając, jak zwykle, że czas zderzenia pręta z sześcianem jest mały, możemy pominąć pęd siły tarcia działającej na sześcian od strony płaszczyzny w porównaniu z pędem siły działającej na sześcian od strony poprzeczki podczas uderzenia. Ponieważ przemieszczenie pręta podczas uderzenia jest niewielkie, aw momencie zetknięcia się sześcianu ze sprężyną nie ulega deformacji w zależności od stanu problemu, zakładamy, że sprężyna nie działa na pręt podczas uderzenia. Dlatego układ „słupek – sześcian” podczas zderzenia można uznać za zamknięty. Następnie, zgodnie z prawem zachowania pędu, zależność
Mw=M u + M ty, (1)
Gdzie u I u- odpowiednio prędkość pręta i sześcianu bezpośrednio po zderzeniu. Praca sił grawitacji i składowa normalna sił reakcji płaszczyzny działającej na sześcian i pręt jest równa zeru (siły te są prostopadłe do ich możliwych przemieszczeń), uderzenie pręta w sześcian jest doskonale sprężysty, a ze względu na krótki czas trwania zderzenia przemieszczenie sześcianu i pręta (a co za tym idzie siły tarcia i odkształcenia sprężyny) można pominąć. Dlatego energia mechaniczna rozważanego układu musi pozostać niezmieniona i zachodzi równość
M υ 2/2 = MU 2/2 + mi 2 /2 (2)
Wyznaczanie z (1) prędkości pręta u i podstawiając to do (2), otrzymujemy 2 Mwu=(M+M)u 2 , a ponieważ stan problemu M << M, następnie 2 wu=u 2. Stąd biorąc pod uwagę możliwy kierunek ruchu wynika, że sześcian po zderzeniu nabiera prędkości, której wartość
![]() (3)
(3)
a prędkość bloku pozostaje niezmieniona i równa w. Dlatego po zderzeniu prędkość sześcianu musi dwukrotnie przekroczyć prędkość pręta. Dlatego po uderzeniu sześcianu w kierunku poziomym, aż się zatrzyma, działa tylko siła tarcia ślizgowego μ mg w konsekwencji sześcian będzie poruszał się ruchem jednostajnym z przyspieszeniem μ G. Na pręcie po zderzeniu w kierunku poziomym działa tylko siła sprężystości sprężyny (pręt jest gładki). Dlatego prędkość klocka zmienia się zgodnie z prawem harmonicznym, a gdy sześcian się porusza, wyprzedza klocek. Z powyższego wynika, że pręt z położenia równowagi można przesunąć o odległość ∆ X. Jeśli współczynnik tarcia μ jest wystarczająco mały, nie będzie powtarzającego się zderzenia pręta z sześcianem, dlatego wymagane przemieszczenie sześcianu powinno wynosić
Ł = I 2 / 2μg = 2 k(∆x) 2 / μ M G.
Porównanie tej odległości z ∆ X, otrzymujemy, że podana odpowiedź jest poprawna dla μ ≤ 2 k ∆X/ Mg
Zadanie 6(2000). Na krawędzi deski leżącej na gładkiej płaszczyźnie poziomej umieść małą podkładkę, której masa wynosi k razy mniej niż masa deski. Krążek zostaje kliknięty w ruch w kierunku środka planszy. Jeśli ta prędkość jest większa u, następnie krążek zsuwa się z planszy. Z jaką prędkością porusza się plansza, jeśli prędkość krążka wynosi N razy więcej u (N> 1)?
Rozwiązanie. Rozwiązując zadanie, jak zwykle pominiemy wpływ powietrza i założymy, że układ odniesienia związany ze stołem jest inercyjny, a krążek po uderzeniu porusza się do przodu. Należy zauważyć, że jest to możliwe tylko wtedy, gdy linia działania impulsu siły zewnętrznej i środek masy krążka leżą w tej samej płaszczyźnie pionowej. Ponieważ, w zależności od stanu problemu, pralka przy początkowej prędkości mniejszej niż u, nie zsuwa się z planszy, należy przyjąć, że gdy krążek ślizga się po planszy, działają między nimi siły tarcia. Biorąc pod uwagę, że po kliknięciu krążek przesuwa się wzdłuż planszy do swojego środka, a siła tarcia ślizgowego jest skierowana przeciwnie do prędkości, można stwierdzić, że plansza również powinna zacząć przesuwać się do przodu po stole. Z powyższego oraz zasady zachowania pędu (ponieważ szachownica leży na gładkiej płaszczyźnie poziomej) wynika, że prędkość krążka bezpośrednio po kliknięciu wynosi u sz, jej prędkość w w i prędkość deski V e w momencie poślizgu podkładki muszą spełniać zależność
Mu w = M V d + Mw w,(1)
Gdzie M jest masą krążka i M- masa deski, jeśli u w > u. Jeśli u w ≤ u, to zgodnie z warunkami zadania krążek nie zsuwa się z planszy, a zatem po odpowiednio długim czasie prędkości krążka i krążka powinny się wyrównać. Zakładając, jak zwykle, wartość siły tarcia suchego ślizgu nie zależy od prędkości, pomijając wymiary podkładki i biorąc pod uwagę, że ruch podkładki względem deski w momencie poślizgu nie zależy od jego prędkość początkowa, biorąc pod uwagę powyższe i opierając się na prawie zmiany energii mechanicznej, możemy stwierdzić, że co przy u w ≥ u
mu w 2 / 2 = MV re 2 / 2 + Mυ w 2 / 2 + A,(2)
Gdzie A- praca przeciwko siłom tarcia i przy u w > u V D< w w i o godz u w = u V re = w cii. Biorąc to pod uwagę, zgodnie z warunkiem M/M=k, z (1) i (2) z u w = u po przekształceniach algebraicznych otrzymujemy
a od godz u w = nu z (1) wynika, że
υ w 2 = N 2 I 2 + k 2 V d 2 - 2 nki V d (4)
pożądana prędkość deski musi spełniać równanie
k(k + 1) V d 2 - 2 nkv d + ki 2 /(k + 1) = 0. (5)
Wiadomo, że o godz N→∞ czas interakcji krążka z deską powinien dążyć do zera, a zatem pożądana prędkość deski wraz ze wzrostem N(po przekroczeniu pewnej wartości krytycznej) powinna się zmniejszyć (do zera). Zatem z dwóch możliwych rozwiązań równania (5) warunki problemu są spełnione przez
Zadanie z fizyki - 4424
2017-10-21
Lekka sprężyna o sztywności k jest przymocowana do pręta o masie m leżącego na płaszczyźnie poziomej, którego drugi koniec jest unieruchomiony tak, że sprężyna nie ulega odkształceniu, a jej oś jest pozioma i przechodzi przez środek pręta. masa pręta Pręt jest mieszany wzdłuż osi sprężyny o odległość $ \Delta L$ i zwalniany bez prędkości początkowej. Znajdź maksymalną prędkość pręta, jeśli jego współczynnik tarcia na płaszczyźnie jest równy $\mu$.
Rozwiązanie:
Przyjmiemy, że dla danego mieszania pręta odkształcenie sprężyny jest w pełni sprężyste. Wtedy na podstawie prawa Hooke'a możemy przyjąć, że siła $F_(pr) = k \Delta L$, skierowana poziomo wzdłuż osi sprężyny, działa na pręt od strony sprężyny w momencie zwolnienia. Siłę reakcji płaszczyzny działającej na pręt można przedstawić jako dwie składowe: prostopadłą i równoległą do tej płaszczyzny. Wartość składowej normalnej siły reakcji $N$ można wyznaczyć na podstawie drugiego prawa Newtona, zakładając, że układ odniesienia ustalony względem tej płaszczyzny jest bezwładny, a pręt może poruszać się tylko wzdłuż tej płaszczyzny. Pomijając działanie na słupek powietrza, otrzymujemy: $N - mg = 0$, gdzie $g$ jest wartością przyspieszenia swobodnego spadku. Zgodnie z prawem Coulomba, przy stałym słupku, maksymalna wartość równoległości składowa siły reakcji - siła tarcia suchego statycznego - jest równa $\mu N $. Zatem dla $k \Delta L \leq \mu mg$ pręt musi pozostać nieruchomy po zwolnieniu. Jeżeli $k \Delta L > \mu mg$, to po zwolnieniu pręta pręt zacznie się poruszać z pewnym przyspieszeniem.Ponieważ linia działania siły co po stronie sprężyny przechodzi przez środek masy pręta, a siła tarcia jest skierowana przeciwnie do jego prędkości, pręt będzie się poruszał postępowo. W takim przypadku odkształcenie sprężyny zmniejszy się, a co za tym idzie przyspieszenie pręta również powinno się zmniejszyć. W momencie, gdy suma sił działających na pręt zamienia się w Jeśli jak zwykle przyjmiemy, że wartość siły tarcia suchego ślizgowego nie zależy od prędkości i jest równa maksymalnej wartości siły tarcia suchego spoczynkowego, to pomijając masę sprężyny w zależności od warunku problemu wartość odkształcenia $\Delta x $ sprężyn w interesującym nas momencie można łatwo obliczyć z zależności $k \Delta x = \mu mg$. Przywołując wyrażenia służące do obliczania energii kinetycznej ciała sztywnego poruszającego się ruchem postępowym, energii potencjalnej sprężyny odkształconej elastycznie i biorąc pod uwagę, że przemieszczenie pręta w tym momencie będzie wynosić $\Delta L - \Delta x$, na podstawie na prawie zmiany energii mechanicznej można argumentować, że maksymalna prędkość pręta $v_(max)$ musi spełniać równanie:
$\frac(k \Delta L^(2))(2) = \frac(k \Delta x^(2))(2) + \frac(mv_(max)^(2))(2) + \ mu mg (\Delta L - \Delta x)$.
Z tego co zostało powiedziane wynika, że maksymalna prędkość pręta, przy przyjętych założeniach, powinna być równa
$v_(max) = \begin(przypadki) 0, & \text(kiedy) k \Delta L \leq \mu mg \\ \sqrt( \frac(k)(m)) \left (\Delta L - \ frac( \mu mg)(k) \right) & \text(at) k \Delta L > \mu mg \end(cases)$.