Мода и медиана – особого рода средние, которые используются для изучения структуры вариационного ряда. Их иногда называют структурными средними, в отличие от рассмотренных ранее степенных средних.
Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности, т.е. имеет наибольшую частоту.
Мода имеет большое практическое применение и в ряде случаев только мода может дать характеристику общественных явлений.
Медиана – это варианта, которая находится в середине упорядоченного вариационного ряда.
Медиана показывает количественную границу значения варьирующего признака, которой достигла половина единиц совокупности. Применение медианы наряду со средней или вместо нее целесообразно при наличии в вариационном ряду открытых интервалов, т.к. для вычисления медианы не требуется условное установление границ отрытых интервалов, и поэтому отсутствие сведений о них не влияет на точность вычисления медианы.
Медиану применяют также тогда, когда показатели, которые нужно использовать в качестве весов, неизвестны. Медиану применяют вместо средней арифметической при статистических методах контроля качества продукции. Сумма абсолютных отклонений варианты от медианы меньше, чем от любого другого числа.
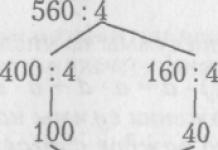
Рассмотрим расчет моды и медианы в дискретном вариационном ряду:
Определить моду и медиану.
Мода Мо = 4 года, так как этому значению соответствует наибольшая частота f = 5.
Т.е. наибольшее число рабочих имеют стаж 4 года.
Для того, чтобы вычислить медиану, найдем предварительно половину суммы частот. Если сумма частот является числом нечетным, то мы сначала прибавляем к этой сумме единицу, а затем делим пополам:
Медианой будет восьмая по счету варианта.
Для того, чтобы найти, какая варианта будет восьмой по номеру, будем накапливать частоты до тех пор, пока не получим сумму частот, равную или превышающую половину суммы всех частот. Соответствующая варианта и будет медианой.
Ме = 4 года.
Т.е. половина рабочих имеет стаж меньше четырех лет, половина больше.
Если сумма накопленных частот против одной варианты равна половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Вычисление моды и медианы в интервальном вариационном ряду
Мода в интервальном вариационном ряду вычисляется по формуле
![]()
где Х М0 - начальная граница модального интервала,
h м 0 – величина модального интервала,
f м 0 , f м 0-1 , f м 0+1 – частота соответственно модального интервала, предшествующего модальному и последующего.
Модальным называется такой интервал, которому соответствует наибольшая частота.
Пример 1
|
Группы по стажу |
Число рабочих, чел |
Накопленные частоты |
Определить моду и медиану.
Модальный интервал , т.к. ему соответствует наибольшая частота f = 35. Тогда:
Хм 0 =6, fм 0 =35
Слепнев Павел
В курсе алгебры 7 класса в учебнике под редакцией Теляковского предлагается материал из статистики "Среднее арифметическое, размах и мода". Учащийся в своей работе предлагает примеры для рассмотрения этой темы, которые предложили его одноклассники.
Скачать:
Предварительный просмотр:
МУ Отдел образования МО «Тарбагатайский район»
МБОУ «Заводская ООШ»
«Среднее арифметическое, размах и мода»
Выполнил: Слепнев Павел, ученик 7 класса
Научный руководитель:
Улаханова Марина Родионовна,
учитель математики
2012 год
Введение Стр. 3
Основная часть Стр.4-9
Теория вопроса Стр.4-6
Мини-проекты Стр.7-9
Заключение Стр.9
Список литературы Стр.10
Введение
Актуальность
В этом учебном году мы начали изучать два предмета: алгебру и геометрию. При изучении алгебры что-то мне знакомо из курса 5,6 классов, что-то мы изучаем более основательно и углубленно, многое узнаем нового. Вот новое для меня при изучении алгебры – это знакомство с некоторыми статистическими характеристиками: размах и мода. Со средним арифметическим мы встречались уже ранее. Еще интересным оказалось, что эти характеристики применяются не только на уроках математики, но и в жизни, на практике (в производстве, в сельском хозяйстве, в спорте и т.д.).
Постановка проблемы
Когда мы в классе на уроке решали задачи к этому пункту, то возникла идея составить самим задачи и подготовить к ним презентации, то есть как бы начать создавать свой задачник. Каждый придумывает задачу, делает к ней презентацию, как бы каждый работает над своим мини-проектом, а на уроке все вместе решаем, обсуждаем. Если допущены ошибки, то их исправляем. А в конце провести публичную защиту этих мини-проектов.
Цель моей работы: изучение статистики.
Задачи: начать разработку задачника по статистике в виде компьютерных презентаций.
Предмет исследования: статистика.
Объект исследования: статистические характеристики (среднее арифметическое, размах, мода).
Методы исследования:
- Изучение литературы по данной теме.
- Анализ данных.
- Использование Интернет-ресурсов.
- Использование программы Power Point.
- Обобщение собранных материалов по данной теме.
Основная часть.
Теория вопроса
В ходе изучения раздела «Статистические характеристики» мы познакомились с такими понятиями: среднее арифметическое, размах, мода. Эти характеристики находят применение в статистике. Эта наука изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т.п.
“Статистика знает всё”, – утверждали Ильф и Петров в своем знаменитом романе “Двенадцать стульев” и продолжали: “Известно, сколько какой пищи съедает в год средний гражданин республики… Известно, сколько в стране охотников, балерин, станков, велосипедов, памятников, маяков и швейных машинок… Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических таблиц!..” Это ироническое описание дает довольно точное представление о статистике (от лат. status – состояние) – науке, изучающей, обрабатывающей и анализирующей количественные данные о самых разнообразных массовых явлениях в жизни.
Экономическая статистика изучает изменение цен, спроса и предложения на товары, прогнозирует рост и падение производства и потребления.
Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий.
Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный).
А еще есть статистика финансовая, налоговая, биологическая, метеорологическая.
В школьном курсе алгебры мы рассматриваем понятия и методы описательной статистики, которая занимается первичной обработкой информации и вычислением наиболее показательных числовых характеристик. По словам английского статистика Р. Фишера: “Статистика может быть охарактеризована как наука о сокращении и анализе материала, полученного в наблюдениях”. Всю совокупность числовых данных, полученных в выборке можно (условно) заменить несколькими числовыми параметрами, некоторые из них мы уже рассматривали на уроках – это среднее арифметическое, размах, мода. Результаты статистических исследований широко используются для практических и научных выводов, поэтому важно уметь определять эти статистические характеристики.
Статистические характеристики в наше время встречаются везде. Например, перепись населения. Благодаря этой переписи, государство узнает сколько нужно денег на строительство жилья, школ, больниц, сколько людей нуждаются в жилье, сколько детей в семье, количество безработных, уровень зарплаты и т.д. Результаты этой переписи сравнят с прошлой, посмотрят поднялась ли страна за это время или положение стало хуже, можно будет сравнить данные с результатами в других странах. В промышленности большое значение имеет мода. Например, товар, который имеет большой спрос - будут всегда продавать, а фабрики будут иметь большие деньги. И таких примеров множество.
Результаты статистических исследований широко используются для практических и научных выводов.
Определение 1. Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Пример: При изучении учебной нагрузки выделили группу из 12 учащихся 7 класса. Просили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25. Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания по алгебре. Для этого надо сложить указанные 12 чисел и полученную сумму разделить
на 12: ==27.
Число 27, полученное в результате, называют средним арифметическим рассматриваемого ряда чисел.
Среднее арифметическое является важной характеристикой ряда чисел но иногда полезно рассматривать и другие средние.
Определение 2. Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Пример: При анализе сведений о времени, затраченном учащимися на выполнение домашнего задания по алгебре, нас могут заинтересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Например, интересно знать, какой расход времени является типичным для выделенной группы учащихся, т.е. какое число встречается в ряду данных чаще всего. Нетрудно заметить, что в нашем примере это число 25. говорят, что число 25 – мода рассматриваемого ряда.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем. Например, в ряду чисел 47, 46, 50, 47, 52, 49, 45, 43, 54, 52, 47, 52 две моды – это числа 47 и 52, так как каждое из них встречается в ряду по три раза, а остальные числа – менее трех раз.
В ряду чисел 69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72 моды нет.
Моду ряда данных обычно находят, когда хотят выявить некоторый типичный показатель. Мода-показатель, который широко используется в статистике. Одним из наиболее частых использований моды является изучение спроса. Например, при решении вопросов, в пачки какого веса фасовать масло, какие открывать авиарейсы и т. п., предварительно изучается спрос и выявляется мода - наиболее часто встречающийся заказ.
Однако нахождение среднего арифметического или моды далеко не всегда позволяет делать надежные выводы на основе статистических данных. если у нас есть ряд данных, то для обоснованных выводов и надежных прогнозов на их основе, помимо средних значений, надо еще указать, насколько используемые данные различаются между собой. Одним из статистических показателей различия или разброса данных является размах.
Определение 3. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Пример: В рассмотренном выше примере мы нашли, что в среднем учащиеся затратили на выполнение домашнего задания по алгебре по 27 минут. Однако анализ проведенного ряда данных показывает, что время, затраченное некоторыми учащимися, существенно отличается от 27 минут, т.е. от среднего арифметического. Наибольший расход равен 37 минут, а наименьший – 18 минут. Разность между наибольшим и наименьшим расходом времени составляет 19 минут. Вот в этом случае рассматривается еще одна статистическая характеристика – размах. Размах ряда находят, когда хотят определить, как велик разброс данных в ряду.
Мини-проекты
А теперь хочу представить результаты нашей работы: мини-проекты для создания задачника по статистике.
Я работаю в салоне-магазине «Супер-авто» главным менеджером отдела продаж. Наш салон предоставлял автомобили для участия в игре «полный привод». В прошлом году на выставке-продаже наши машины имели успех! Результаты продаж следующие:
Продано машин в первый день | Продано машин во второй день | Продано машин в третий день | Продано машин в четвертый день | Продано машин в пятый день |
Отделу продаж необходимо подвести итоги выставки:
- Сколько в среднем продавалось машин в день?
- Каков разброс количества машин за период выставки-продажи?
- Сколько чаще всего продавалось машин в день?
Ответ: в среднем было продано по 150 машин в день, разброс количества проданных машин составил – 150, в день чаще всего продавалось 100 машин.
Я, Анастасия Волочкова, была приглашена в жюри на финал конкурса «Лёд и пламя». Конкурс проходил в городе Санкт –Петербурге. В финал вышли три пары самых сильных фигуристов: 1пара. Батуева Алина и Хлебодаров Кирилл, 2 пара. Селянская Юлия и Кушнарев Павел, 3пара. Заиграева Анастасия и Афанасьев Дмитрий. Жюри: Анастасия Волочкова, Елена Малышева, Алексей Далматов. Жюри выставили следующие оценки:
Найдите среднее арифметическое, размах моду в рядах оценок каждой пары.
Ответ:
Итоги | Среднее арифметическое | Размах | Мода |
1 пара | 5.43 | ||
2 пара | 5.27 | ||
3 пара | 5.23 | нет |
В этом году я побывала в г. Санкт-Петербург на соревнованиях по бальным танцам. В конкурсе принимали участие три красивые пары: Сушенцова Елена и Хлебодаров Кирилл, Батуева Алина и Слепнев Павел, Джаниашвили Виктория и Ткачев Валерий.
За выступления пары получили следующие оценки:
Найти среднюю оценку, размах и моду.
Ответ:
Пары | Среднее арифметическое | Размах | Мода |
№1 | 4,42 | ||
№2 | 4,37 | ||
№3 | 4,37 |
Я директор магазина модной одежды и аксессуаров «Fashion». Магазин приносит хорошую прибыль. Показатели продаж за прошлый год:
915т.р. | 1млн 150т.р. | 1 млн. 980т.р. | 2 млн. 3т.р. | 2 млн. 950т.р. | 3 млн. 950т.р. | 3 млн. 100т.р. | 2 млн. 950т.р. | 3 млн. | 3 млн. 750т.р. | 2млн. 950т.р. | 4 млн. 250т.р. |
Первые 2-3 месяца прибыль доходила до 2 миллионов за месяц. Уже после прибыль возрастала до 4 миллионов. Самыми удачными месяцами были: декабрь и май. В мае в основном покупали платья для выпускных баллов, а в декабре для новогоднего торжества.
Вопрос моему главному бухгалтеру: каковы результаты нашей работы за год?
Ответ:
Среднее арифметическое | 2 745 000 руб |
Размах | 4 158 500 руб |
Мода | 2 950 000 руб |
Мы организовали тюнинг-мастерскую «Turbo». За первую неделю нашей работы мы заработали: в первый день – 120 000 $, во второй день – 350 000 $, в третий день – 99 000$, в четвертый день – 120 00$. Подсчитайте каков наш средний доход в день, коков разрыв между наибольшим и наименьшим заработком и какая сумма чаще повторяется?
Ответ: среднее арифметическое – 172 250 $, размах – 251 000 $, мода – 120 000 $.
Заключение
В заключении я хочу сказать, что мне нравится эта тема. Статистические характеристики очень удобны, их можно применять везде. В общем, они сравнивают, стремятся к прогрессу и помогают узнать мнение народа. В ходе работы над этой темой я познакомился с наукой статистикой, узнал некоторые понятия (среднее арифметическое, размах и мода), где эта наука может быть применима, расширил свои познания и в информатике. Я, думаю, что наши задачки как примеры для освоения этих понятий пригодятся и другим! Будем продолжать знакомство в этой наукой и создавать свои задачки!
Вот и закончилось мое путешествие в мир математики, информатики и статистики. Но я, думаю, что не последнее. Я еще многое хочу познать! Как сказал Галилео Галилей: «Природа формулирует свои законы языком математики». И я хочу овладеть этим языком!
Список литературы
- Бунимович Е.А., Булычев В.А. « Вероятность и статистика в курсе математики общеобразовательной школы», М.: Педагогический университет “Первое сентября”, 2005
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. «Алгебра, 7 класс», М: «Просвещение», 2009
- Макарычев Ю.Н., Миндюк Н.Г. « Алгебра. Элементы статистики и теории вероятностей», 7 – 9 классы. – М.: Просвещение, 2005.
Рецензия
Предметом исследования учащегося является статистика.
Объектом исследования – статистические характеристики (среднее арифметическое, размах, мода).
Ученик для ознакомления с теорией вопроса изучил научные источники, Интернет-ресурсы.
Выбранная тема актуальна для учащегося, проявляющего интерес к математике, информатике, статистике. Для его возраста проанализирован достаточный материал, произведен отбор данных, обобщен. Учащийся достаточно владеет ИКТ.
Работа оформлена в соответствии с требованиями.
В конце исследования сделан вывод, представлен практический продукт: презентации задач по статистике. Радует, что человек так увлечен математикой.
Научный руководитель: Улаханова МР,
учитель математики
Наряду со средними величинами в качестве статистических характеристик вариационных рядов распределения рассчитываются структурные средние – мода
и медиана
.
Мода
(Mo) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой, т.е. мода – значение признака, встречающееся чаще всего.
Медианой
(Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности, т.е. медиана – центральное значение вариационного ряда.
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины ∑|x i - Me|=min.
Определение моды и медианы по несгруппированным данным
Рассмотрим определение моды и медианы по несгруппированным данным . Предположим, рабочие бригады, состоящей из 9 человек, имеют следующие тарифные разряды: 4 3 4 5 3 3 6 2 6 . Так как в данной бригаде больше всего рабочих 3-го разряда, этот тарифный разряд будет модальным. Mo = 3.Для определения медианы необходимо провести ранжирование: 2 3 3 3 4 4 5 6 6 . Центральным в этом ряду является рабочий 4-го разряда, следовательно, данный разряд и будет медианным. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений.
Если мода отражает наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределения совокупности. Проиллюстрируем ее познавательное значение следующим примером.
Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 100 до 200 долларов в месяц, а месячные доходы последнего составляют 50000 долларов (табл. 1).
Таблица 1 - Месячные доходы исследуемой группы людей. Если воспользоваться средней арифметической, то получим средний доход, равный примерно 600 – 700 долларов, который имеет мало общего с доходами основной части группы. Медиана же, равная в данном случае Me = 163 доллара, позволит дать объективную характеристику уровня доходов 99 % данной группы людей.
Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).
Предположим, распределение рабочих всего предприятия в целом по тарифному разряду имеет следующий вид (табл. 2).
Таблица 2 - Распределение рабочих предприятия по тарифному разряду
Расчет моды и медианы для дискретного ряда
Расчет моды и медианы для интервального ряд
Расчет моды и медианы для вариационного ряда
Определение моды по дискретному вариационному ряду
Используется построенный ранее ряд значений признака, отсортированных по величине. Если объем выборки нечетный, берем центральное значение; если объем выборки четный, берем среднее арифметическое двух центральных значений.Определение моды по дискретному вариационному ряду : наибольшую частоту (60 человек) имеет 5-й тарифный разряд, следовательно, он и является модальным. Mo = 5.
Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда (N Me): , где n - объем совокупности.
В нашем случае:
 .
.
Полученное дробное значение, всегда имеющее место при четном числе единиц совокупности, указывает, что точная середина находится между 95 и 96 рабочими. Необходимо определить, к какой группе относятся рабочие с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Рабочих с этими номерами нет в первой группе, где всего лишь 12 человек, нет их и во второй группе (12+48=60). 95-й и 96-й рабочие находятся в третьей группе (12+48+56=116), следовательно, медианным является 4-й тарифный разряд.
Расчет моды и медианы в интервальном ряду
В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул: , (5.6)
, (5.6)
где x 0 – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
i – величина модального интервала;
f Mo – частота модального интервала;
f Mo -1 – частота интервала, предшествующего модальному;
f Mo +1 – частота интервала, следующего за модальным.
 (5.7)
(5.7)
где x 0 – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
i – величина медианного интервала;
S Me -1 – накопленная интервала, предшествующего медианному;
f Me – частота медианного интервала.
Проиллюстрируем применение этих формул, используя данные табл. 3.
Интервал с границами 60 – 80 в данном распределении будет модальным, т.к. он имеет наибольшую частоту. Использую формулу (5.6), определим моду:
Для установления медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит половины суммы накопленных частот (в нашем случае 50 %) (табл. 5.11).
Установили, что медианным является интервал с границами 100 – 120 тыс. руб. Определим теперь медиану:
Таблица 3 - Распределение населения РФ по уровню среднедушевых номинальных денежных доходов в марте 1994г.
| Группы по уровню среднедушевого месячного дохода, тыс. руб. | Удельный вес населения, % |
| До 20 | 1,4 |
| 20 – 40 | 7,5 |
| 40 – 60 | 11,9 |
| 60 – 80 | 12,7 |
| 80 – 100 | 11,7 |
| 100 – 120 | 10,0 |
| 120 – 140 | 8,3 |
| 140 –160 | 6,8 |
| 160 – 180 | 5,5 |
| 180 – 200 | 4,4 |
| 200 – 220 | 3,5 |
| 220 – 240 | 2,9 |
| 240 – 260 | 2,3 |
| 260 – 280 | 1,9 |
| 280 – 300 | 1,5 |
| Свыше 300 | 7,7 |
| Итого | 100,0 |
Таблица 4 - Определение медианного интервала
Таким образом, в качестве обобщенной характеристики значений определенного признака у единиц ранжированной совокупности могут быть использованы средняя арифметическая, мода и медиана.
Основной характеристикой центра распределения является средняя арифметическая, для которой характерно то, что все отклонения от нее (положительные и отрицательные) в сумме равняются нулю. Для медианы характерно, что сумма отклонений от нее по модулю является минимальной, а мода представляет собой значение признака, которое наиболее часто встречается.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. В симметричных распределениях все три характеристики совпадают. Чем больше расхождение между модой и средней арифметической, тем более асимметричен ряд. Для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней, т.е.:
|Mo –`x| = 3 |Me –`x|.
Определение моды и медианы графическим методом
Моду и медиану в интервальном ряду можно определить графически . Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Из точки их пересечения опускаем перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения (рис. 5.3).
Рис. 5.3. Графическое определение моды по гистограмме.

Рис. 5.4. Графическое определение медианы по кумуляте
Для определения медианы из точки на шкале накопленных частот (частостей), соответствующей 50 %, проводится прямая, параллельная оси абсцисс до пересечения с кумулятой. Затем из точки пересечения опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.
Квартили, децили, перцентили
Аналогично с нахождением медианы в вариационных рядах распределения можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Так, например, можно найти значение признака у единиц, делящих ряд на четыре равные части, на 10 или на 100 частей. Эти величины называются «квартили», «децили», «перцентили».Квартили представляют собой значение признака, делящее ранжированную совокупность на 4 равновеликие части.
Различают квартиль нижний (Q 1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний (Q 3), осекающий ¼ часть с наибольшими значениями признака. Это означает, что 25 % единиц совокупности будут меньше по величине Q 1 ; 25 % единиц будут заключены между Q 1 и Q 2 ; 25 % - между Q 2 и Q 3 , а остальные 25 % превосходят Q 3 . Средним квартилем Q 2 является медиана.
Для расчета квартилей по интервальному вариационному ряду используются формулы:
 ,
,  ,
,
где x Q 1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25 %);
x Q 3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75 %);
i – величина интервала;
S Q 1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
S Q 3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
f Q 1 – частота интервала, содержащего нижний квартиль;
f Q 3 – частота интервала, содержащего верхний квартиль.
Рассмотрим расчет нижнего и верхнего квартилей по данным табл. 5.10. Нижний квартиль находится в интервале 60 – 80, накопленная частота которого равна 33,5 %. Верхний квартиль лежит в интервале 160 – 180 с накопленной частотой 75,8 %. С учетом этого получим:
,
.
Кроме квартилей в вариационных радах распределения могут определяться децили – варианты, делящие ранжированный вариационный ряд на десять равных частей. Первый дециль (d 1) делит совокупность в соотношении 1/10 к 9/10, второй дециль (d 1) – в соотношении 2/10 к 8/10 и т.д.
Вычисляются они по формулам:
 ,
,  .
.
Значения признака, делящие ряд на сто частей, называются перцентилями. Соотношения медианы, квартилей, децилей и перцентилей представлены на рис. 5.5.

Цели: дать понятия, алгоритмы нахождения среднего арифметического и медианы, размаха и моды ряда чисел, показать значимость этой темы в практической деятельности человека; приобретение практических навыков выполнения этих заданий; повышение уровня математической подготовки, предъявляемой новыми стандартами.
- вооружить учащихся системой знаний по теме "Определение вероятности событий, среднего арифметического и медианы набора чисел";
- сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;
- подготовить учащихся к сдаче ГИА;
- сформировать навыки самостоятельной работы.
Ход урока
1. Теоретическая часть.
1). Нахождение вероятности событий.
В повседневной жизни, в практической и научной деятельности часто наблюдают те или иные явления, проводят определенные эксперименты.
В процессе наблюдения или эксперимента приходится встречаться с некоторыми случайными событиями , т. е. такими событиями, которые могут произойти или не произойти. Например, выпадение орла или решки при подбрасывании монеты, поражение мишени или промах при выстреле, выигрыш спортивной команды во встрече с соперником, проигрыш или ничейный результат- все это случайные события.
Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей . Методы теории вероятностей применяются во многих областях знаний.
Зарождение теории вероятностей произошло в поисках ответа на вопрос: как часто наступает то, или иное событие в большой серии происходящих в одинаковых условиях испытаний со случайными исходами.
Для того чтобы оценить вероятность интересующего нас события необходимо провести большое число опытов или наблюдений, и только после этого можно определить вероятность этого события.
Например, бросание игрального кубика. При бросании кубика шансы выпадения на его верхней грани каждого числа очков от 1 до 6 одинаковы. Говорят, что существует 6 равновозможных исходов опыта с бросанием кубика: выпадение 1,2,3,4,5, и 6 очков.
Исходы в этом опыте считают равновозможными, если шансы этих исходов одинаковы.
Исходы, при которых происходит некоторое событие, называются благоприятными исходами для этого события.
Определение: отношение числа благоприятных исходов N (A) события A к числу всех равновозможных исходов N этого события называется вероятностью события A.
Схема нахождения вероятности события.
Для нахождения вероятности случайного события A при проведении некоторого испытания следует:
- найти число N всех равновозможных исходов данного испытания;
- найти количество N(A) тех благоприятных исходов испытания, в которых наступает событие А;
- найти отношение N(A)/N; это и есть вероятность события A
Например: 1 . В коробке лежат 10 красных, 7 желтых и 3 синих шара. Какова вероятность, что взятый наугад шар окажется желтым?
Решение. Равновозможные исходы- (10+7+3)=20
Благоприятные исходы-7
2. В коробке лежит 5 черных шаров. Какое наименьшее число белых шаров нужно положить в эту коробку, чтобы после этого вероятность наугад достать из коробки черный шар была не больше 0,15?
Решение: Пусть x-белые шары.
2) Определение и нахождение среднего арифметического и медианы ряда чисел.
Определение: средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
Среднее арифметическое набора чисел x 1 ,x 2 ,x 3 ,x 4 ,x 5 принято обозначать x.
Например, среднее арифметическое пяти чисел запишется так:
X = (x 1 +x 2 +x 3 +x 4 +x 5)/5
Пример: найти среднюю оценку учащегося по математике, если за истекший период он получил: 3,4,4,5,3,2,4,3.
Решение: (3+4+4+5+3+2+4+3)/8=3,5
Определение: медианой называется число, разделяющее набор чисел на две части, равные по численности, так что с одной стороны от этого числа все значения больше медианы, а с другой меньше. Вместо "медиана" можно было бы сказать середина.
Схема нахождения медианы набора чисел:
Для нахождения медианы набора чисел следует:
- упорядочить числовой набор (записать в порядке возрастания);
- одновременно зачеркиваем "самое большое" и "самое маленькое" числа данного набора чисел до тех пор, пока не останется одно число или два числа;
- если останется одно число, то оно и есть медиана (для нечетного набора чисел);
- если останется два числа, то медианой будет среднее арифметическое двух оставшихся чисел (для четного набора чисел).
Медиану принято обозначать буквой М.
Пример: найти медиану набора чисел: 9,3,1,5,7.
Решение: запишем числа в порядке возрастания: 1,3,5,7,9.
Вычеркнем 1 и 9, 3 и 7. Оставшееся число 5 и есть медиана. М=5
Пример: найти медиану набора чисел 2,3,3,5,7,10.
Решение: вычеркнем 2 и 10, 3 и 7. Для нахождения М нужно: (3+5)/2= 4. М=4
Определение и нахождение размаха и моды.
Определение: размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда находят, когда хотят определить, как велик разброс данных в ряду.
Определение: модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Пример: На уроке физкультуры 14 школьников прыгали в высоту, а учитель записывал их результаты. Получился такой ряд данных (в см):
125, 110, 130, 125, 120, 130, 140, 125, 110, 130, 120, 125, 120, 125.
Найти медиану, размах и моду измерения.
Решение: выпишем все варианты измерения в порядке возрастания, разделяя пробелами группы одинаковых результатов:
110, 110, 120, 120, 120, 125, 125, 125, 125, 125, 130, 130, 130, 140.
Размах измерения равен 140-110=30.
125-встретилось наибольшее число раз, т. е. 5 раз; это мода измерения.
2. Практическая часть.
1). Задачи для самостоятельного решения на теорию вероятностей.
1. На 100 электрических лампочек в среднем приходится 4 бракованных. Какова вероятность, что взятая наугад лампочка окажется исправной? Ответ: 0,96.
2. На 400 компакт-дисков в среднем приходится 8 бракованных. Какова вероятность, что взятый наугад компакт-диск окажется исправным? Ответ: 0,98.
3. 17 точек из 50 покрашены в синий цвет, а 13 точек из оставшихся покрашены в оранжевый цвет. Какова вероятность того, что случайно выбранная точка окажется окрашенной? Ответ: 0,6.
4. Из слова "математика" случайным образом выбирается одна буква. Какова вероятность, что выбранная буква встречается в этом слове только 1 раз? Ответ: 0,3.
5. Из слова "аттестация" случайным образом выбирается одна буква. Какова вероятность, что выбранная буква окажется буквой "а"? Ответ: 0,2
6. Из 30девятиклассников 4 выбрали экзамен по физике, 12 - по обществознанию, 8- по иностранному языку, а остальные по литературе. Какова вероятность, что выбранный ученик будет сдавать экзамен по литературе. Ответ: 0,2.
7. Контрольная работа по математике состоит из 15 задач: 4 задачи по геометрии, 2 задачи по теории вероятностей, остальные по алгебре. Ученик ошибся в одной задаче. Какова вероятность, что ученик ошибся в задаче по алгебре? Ответ: 0,6.
8. На 1000 автомобилей, выпущенных в 2007-2009 г. г., 150 имеют дефект тормозной системы. Какова вероятность купить неисправную машину? Ответ: 0,15.
9. В соревнованиях по художественной гимнастике участвуют: 3 гимнастки из России, 3 гимнастки из Украины и 4 гимнастки из Белоруссии. Порядок выступления определятся жеребьевкой. Найдите вероятность того, что первой будет выступать гимнастка из России. Ответ 0,3
10. На чемпионате по художественной гимнастике выступает 18 гимнасток, среди них 3 гимнастки из России, 2 гимнастки из Китая. Порядок выступления определяется жеребьевкой. Найдите вероятность того, что последней будет выступать гимнастка или из России, или из Китая? Ответ: 5/18.
11. Из класса, в котором учатся 12 мальчиков и 8 девочек, выбирают по жребию 1 дежурного. Какова вероятность того, что это будет мальчик? Ответ: 0,6.
12. Одновременно бросают 2 монеты. С какой вероятностью на них выпадут 2 решки? Ответ 0,25.
2) Задачи на нахождение среднего арифметического и медианы, размаха и моды набора чисел.
Фрезеровщики бригады затратили на обработку одной детали разное время (в мин.), представленное в виде ряда данных: 40; 37; 35; 36; 32; 42; 32; 38; 32. На сколько медиана этого набора отличается от среднего арифметического? Ответ: 0.
В саду посадили 5 саженцев яблони, высота которых в сантиметрах следующая: 168, 13, 156, 165, 144. На сколько отличается среднее арифметическое этого набора чисел от его медианы? Ответ: 3, 8
Растущие в саду 6 деревьев груши дали урожай, масса которого (в кг) для каждого из деревьев следующая: 29, 35, 26, 28, 32, 36. На сколько отличается среднее арифметическое этого набора чисел от его медианы? Ответ: 0,5
Время обслуживания кассиром каждого из нескольких покупателей магазина образовало следующий ряд данных: 2 мин. 42 сек., 3мин. 2 сек., 3 имн. 7сек., 2 мин. 54 сек., 2 мин. 48 сек. Найдите среднее значение и медиану этого ряда данных. Ответ: 2 мин. 55 сек., 2 мин. 54 сек.
Время между семью звонками, поступившими в службу такси образовало следующий ряд данных: 34 сек., 45 сек., 1 мин. 16 сек., 38 сек., 43 сек., 52 сек. Найдите среднее значение и медиану этого ряда данных. Ответ: 48 сек., 44 сек.
Литература: Мордкович, А. Г. ,И. М. Смирновой. Учебнок для общеобразовательных учреждений (базовый уровень) - М.: Мнемозина, 2009. - 164 с.