Twierdzenia o zmianie pędu punktu i układu. Twierdzenie o zmianie pędu układu mechanicznego. Prawo zmiany pędu

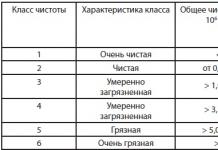
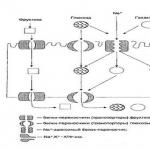
(Fragmenty symfonii matematycznej)

Związek impulsu siły z podstawowym równaniem dynamiki Newtona wyraża twierdzenie o zmianie pędu punktu materialnego.

Twierdzenie. Zmiana pędu punktu materialnego w pewnym okresie czasu jest równa impulsowi siły () działającej na punkt materialny w tym samym okresie czasu. Dowód matematyczny tego twierdzenia można nazwać fragmentem symfonii matematycznej. Tutaj jest.

Różnicowy pęd punktu materialnego jest równy elementarnemu impulsowi siły działającej na punkt materialny. Mamy wyrażenie całkujące (128) dla pędu różniczkowego punktu materialnego

(129)

Twierdzenie zostało udowodnione i matematycy uważają swoją misję za zakończoną, ale inżynierowie, których przeznaczeniem jest święta wiara w matematyków, mają pytania, gdy korzystają ze sprawdzonego równania (129). Blokuje je jednak stanowczo kolejność i piękno operacji matematycznych (128 i 129), które fascynują i zachęcają do nazwania ich fragmentem symfonii matematycznej. Ileż pokoleń inżynierów zgadzało się z matematykami i zachwycało się tajemnicą ich symboli matematycznych! Ale był też inżynier, który nie zgodził się z matematykami i zadał im pytania.

Drodzy matematycy! Dlaczego żaden z Twoich podręczników mechaniki teoretycznej nie omawia procesu zastosowania Twojego symfonicznego wyniku (129) w praktyce, na przykład przy opisie procesu przyspieszania samochodu? Lewa strona równania (129) jest bardzo jasna. Samochód rozpoczyna przyspieszanie od prędkości i kończy je np. przy prędkości. Jest całkiem naturalne, że równanie (129) staje się

I od razu pojawia się pierwsze pytanie: jak z równania (130) wyznaczyć siłę, pod wpływem której samochód rozpędza się do prędkości 10 m/s? Odpowiedzi na to pytanie nie znajdziemy w żadnym z niezliczonych podręczników mechaniki teoretycznej. Idźmy dalej. Po przyspieszeniu samochód zaczyna poruszać się równomiernie z prędkością 10 m/s. Jaka siła porusza samochód???????? Nie pozostaje mi nic innego, jak zarumienić się razem z matematykami. Pierwsza zasada dynamiki Newtona mówi, że gdy samochód porusza się ruchem jednostajnym, nie działają na niego żadne siły, a samochód, mówiąc w przenośni, kicha na to prawo, zużywa benzynę i pracuje, pokonując np. odległość 100 km. Gdzie jest siła, która wykonała pracę, aby przesunąć samochód na odległość 100 km? Symfoniczne równanie matematyczne (130) milczy, ale życie toczy się dalej i domaga się odpowiedzi. Zaczynamy go szukać.

Ponieważ samochód porusza się prostoliniowo i równomiernie, siła poruszająca nim jest stała pod względem wielkości i kierunku, a równanie (130) przyjmuje postać

(131)

Zatem równanie (131) w tym przypadku opisuje przyspieszony ruch ciała. Jaka jest równa siła? Jak wyrazić jego zmianę w czasie? Matematycy wolą pominąć to pytanie i pozostawić je inżynierom, wierząc, że muszą szukać odpowiedzi na to pytanie. Inżynierom pozostaje tylko jedno wyjście - wziąć pod uwagę, że jeśli po zakończeniu przyspieszonego ruchu ciała rozpocznie się faza ruchu jednostajnego, któremu towarzyszy działanie stałej siły, przedstawiamy równanie (131) dla moment przejścia od ruchu przyspieszonego do ruchu jednostajnego w tej postaci

(132)

Strzałka w tym równaniu nie oznacza wyniku całkowania tego równania, ale proces przejścia od jego postaci całkowej do postaci uproszczonej. Siła w tym równaniu jest równa średniej sile, która zmieniła pęd ciała od zera do wartości końcowej. Tak więc, drodzy matematycy i fizycy teoretyczni, brak waszej metody określania wielkości waszego impulsu zmusza nas do uproszczenia procedury wyznaczania siły, a brak metody określania czasu działania tej siły generalnie stawia nas w trudnej sytuacji. pozycja beznadziejna i zmuszeni jesteśmy posłużyć się wyrażeniem analizującym proces zmiany pędu ciała. W rezultacie im dłużej działa siła, tym większy jest jej impuls. Jest to wyraźnie sprzeczne z ugruntowaną od dawna koncepcją, że im krótszy czas działania, tym większy impuls siły.

Zwróćmy uwagę na fakt, że zmiana pędu punktu materialnego (impulsu siły) podczas jego przyspieszonego ruchu następuje pod wpływem siły Newtona i sił oporu ruchu, w postaci sił utworzonych przez opory mechaniczne i siła bezwładności. Jednak dynamika newtonowska w zdecydowanej większości zagadnień ignoruje siłę bezwładności, a mechanodynamika stwierdza, że zmiana pędu ciała podczas jego ruchu przyspieszonego następuje na skutek przewagi siły newtonowskiej nad siłami oporu ruchu, do których zalicza się siła bezwładności.

Kiedy ciało porusza się w zwolnionym tempie, np. samochód z wyłączonym biegiem, nie ma siły Newtona, a zmiana pędu samochodu następuje na skutek przewagi sił oporu ruchu nad poruszającą się siłą bezwładności samochód, gdy porusza się powoli.

Jak możemy teraz przywrócić wyniki zauważonych „symfonicznych” działań matematycznych (128) do głównego nurtu związków przyczynowo-skutkowych? Jest tylko jedno wyjście - znaleźć nową definicję pojęć „impuls siły” i „siła uderzenia”. Aby to zrobić, podziel obie strony równania (132) przez czas t. W efekcie będziemy mieli

. (133)

Zauważmy, że wyrażenie mV/t jest szybkością zmiany pędu (mV/t) punktu lub ciała materialnego. Jeśli weźmiemy pod uwagę, że V/t jest przyspieszeniem, wówczas mV/t jest siłą zmieniającą pęd ciała. Ten sam wymiar po lewej i prawej stronie znaku równości daje nam prawo nazwać siłę F siłą uderzeniową i oznaczyć ją symbolem, a impuls S - impulsem uderzeniowym i oznaczyć go symbolem. Prowadzi to do nowej definicji siły uderzenia. Siła uderzenia działająca na punkt materialny lub ciało jest równa stosunkowi zmiany pędu punktu lub ciała materialnego do czasu tej zmiany.

Zwróćmy szczególną uwagę na fakt, że w powstaniu impulsu uderzeniowego (134), który powoduje zmianę prędkości samochodu od zera do maksymalnej, uczestniczy wyłącznie siła Newtona – dlatego równanie (134) należy w całości do dynamiki Newtona. Ponieważ znacznie łatwiej jest wyznaczyć wielkość prędkości doświadczalnie niż wyznaczyć przyspieszenie, wzór (134) jest bardzo wygodny do obliczeń.

Ten niezwykły wynik wynika z równania (134).

Zwróćmy uwagę, że zgodnie z nowymi prawami mechanodynamiki generatorem impulsu siły podczas przyspieszonego ruchu punktu lub ciała materialnego jest siła Newtona. Tworzy przyspieszenie ruchu punktu lub ciała, przy którym automatycznie powstaje siła bezwładności, skierowana przeciwnie do siły Newtona, a uderzenie Siła Newtona musi pokonać działanie siły bezwładności, dlatego siła bezwładności musi być przedstawiona w postaci bilans sił po lewej stronie równania (134). Ponieważ siła bezwładności jest równa masie punktu lub ciała pomnożonej przez powstałe przez nią opóźnienie, wówczas równanie (134) ma postać

(136)

Drodzy matematycy! Widzicie jaką postać przybrał model matematyczny opisujący impuls uderzeniowy, który przyspiesza ruch uderzanego ciała od prędkości zerowej do maksymalnej V (11). Sprawdźmy teraz jego działanie przy wyznaczaniu impulsu uderzenia, który jest równy sile uderzenia, która wystrzeliła 2. blok napędowy SShG (ryc. 120), a pozostawimy cię z bezużytecznym równaniem (132). Aby nie komplikować prezentacji, pozostawimy na razie wzór (134) w spokoju i posłużymy się wzorami, które podają średnie wartości sił. Widzisz na jakiej pozycji stawiasz inżyniera próbującego rozwiązać konkretny problem.

Zacznijmy od dynamiki Newtona. Eksperci ustalili, że drugi blok napędowy wzniósł się na wysokość 14 m. Ponieważ wznosił się w polu grawitacyjnym, na wysokości h = 14 m jego energia potencjalna okazała się równa

a średnia energia kinetyczna była równa

Ryż. 120. Zdjęcie turbinowni przed katastrofą

Z równości energii kinetycznej (138) i potencjalnej (137) wynika średnia szybkość wzrostu jednostki napędowej (ryc. 121, 122)

Ryż. 121. Foton turbinowni po katastrofie

Zgodnie z nowymi prawami mechanodynamiki wzrost zespołu napędowego składał się z dwóch faz (ryc. 123): pierwszej fazy OA – przyspieszonego wzrostu i drugiej fazy AB – powolnego wzrostu, , .

Czas i odległość ich działania są w przybliżeniu równe (). Następnie równanie kinematyczne fazy przyspieszonej podnoszenia zespołu napędowego zostanie zapisane w następujący sposób:

. (140)

Ryż. 122. Widok studni bloku energetycznego i samego bloku energetycznego po katastrofie

Prawo zmiany szybkości narastania bloku energetycznego w pierwszej fazie ma postać

. (141)

Ryż. 123. Regularność zmian prędkości lotu V zespołu napędowego

Podstawiając czas z równania (140) do równania (141), mamy

. (142)

Czas podnoszenia bloku w pierwszej fazie wyznacza się ze wzoru (140)

. (143)

Wówczas całkowity czas podniesienia zespołu napędowego na wysokość 14 m będzie równy . Masa zespołu napędowego i pokrywy wynosi 2580 ton. Zgodnie z dynamiką Newtona siła, która podniosła jednostkę napędową, jest równa

Drodzy matematycy!Śledzimy Twoje symfoniczne wyniki matematyczne i zapisujemy Twój wzór (129), zgodnie z dynamiką Newtona, aby określić impuls uderzeniowy, który wystrzelił drugi zespół napędowy

i zadaj podstawowe pytanie: jak ustalić czas trwania impulsu uderzeniowego, który wystrzelił 2. blok napędowy????????????

Droga!!! Pamiętajcie, ile kredy napisały na tablicach pokolenia waszych kolegów, w zawiły sposób ucząc uczniów, jak określić impuls uderzeniowy, a nikt nie wyjaśnił, jak określić czas trwania impulsu uderzeniowego w każdym konkretnym przypadku. Powiecie, że czas trwania impulsu uderzeniowego jest równy odstępowi czasu zmiany prędkości zespołu napędowego od zera do, założymy, maksymalnej wartości 16,75 m/s (139). Jest we wzorze (143) i wynosi 0,84 s. Na razie się z Tobą zgadzamy i określamy średnią wartość impulsu uderzeniowego

Natychmiast pojawia się pytanie: dlaczego wielkość impulsu uderzeniowego (146) jest mniejsza niż siła Newtona wynosząca 50600 ton? Wy, drodzy matematycy, nie macie odpowiedzi. Idźmy dalej.

Zgodnie z dynamiką Newtona główną siłą, która przeciwdziałała unoszeniu się jednostki napędowej, była grawitacja. Ponieważ siła ta jest skierowana przeciwnie do ruchu jednostki napędowej, generuje ona opóźnienie równe przyspieszeniu swobodnego spadania. Wtedy siła grawitacji działająca na lecący w górę zespół napędowy jest równa

Dynamika Newtona nie uwzględnia innych sił, które uniemożliwiły działanie siły Newtona o masie 50 600 ton (144), a mechanodynamika stwierdza, że wzrostowi zespołu napędowego przeciwstawiła się także siła bezwładności równa

Natychmiast pojawia się pytanie: jak znaleźć wielkość opóźnienia w ruchu jednostki napędowej? Dynamika Newtona milczy, ale odpowiada mechanodynamika: w momencie działania siły Newtona, która uniosła jednostkę napędową, stawiały jej opór: siła ciężkości i siła bezwładności, stąd równanie sił działających na moc jednostka w tym momencie jest zapisana w następujący sposób.

Równanie różniczkowe ruchu punktu materialnego pod wpływem siły F można przedstawić w następującej postaci wektorowej:

Ponieważ masa punktu M przyjmuje się jako stałą, wówczas można ją wpisać pod znakiem pochodnej. Następnie

Wzór (1) wyraża twierdzenie o zmianie pędu punktu w postaci różniczkowej: pierwsza pochodna po czasie pędu punktu jest równa sile działającej na ten punkt.

W rzutach na osie współrzędnych (1) można przedstawić jako

Jeśli obie strony (1) zostaną pomnożone przez dt, wówczas otrzymujemy inną postać tego samego twierdzenia - twierdzenie o pędzie w postaci różniczkowej:

te. różnica pędu punktu jest równa elementarnemu impulsowi siły działającej na ten punkt.

Rzutując obie części (2) na osie współrzędnych otrzymujemy

Całkując obie części (2) od zera do t (ryc. 1), mamy

gdzie jest prędkość punktu w danej chwili T; - prędkość w T = 0;

S- impuls siły w czasie T.

Wyrażenie w postaci (3) jest często nazywane twierdzeniem o pędzie w postaci skończonej (lub całkowej): zmiana pędu punktu w dowolnym okresie czasu jest równa impulsowi siły w tym samym okresie.

W rzutach na osie współrzędnych twierdzenie to można przedstawić w następującej postaci:

W przypadku punktu materialnego twierdzenie o zmianie pędu w dowolnej postaci zasadniczo nie różni się od równań różniczkowych ruchu punktu.

Twierdzenie o zmianie pędu układu

Wielkość ruchu układu będzie nazywana wielkością wektorową Q, równa sumie geometrycznej (wektorowi głównemu) wielkości ruchu wszystkich punktów układu.

Rozważmy system składający się z N punkty materialne. Ułóżmy równania różniczkowe ruchu dla tego układu i dodajmy je wyraz po wyrazie. Następnie otrzymujemy:

Ostatnia suma, ze względu na właściwość sił wewnętrznych, jest równa zeru. Oprócz,

Wreszcie znajdujemy:

Równanie (4) wyraża twierdzenie o zmianie pędu układu w postaci różniczkowej: pochodna czasowa pędu układu jest równa sumie geometrycznej wszystkich sił zewnętrznych działających na układ.

Znajdźmy inne wyrażenie dla twierdzenia. Wpuść tę chwilę T= 0 oznacza wielkość ruchu układu Pytanie 0 i w danym momencie t 1 staje się równy Pytanie 1. Następnie mnożąc obie strony równości (4) przez dt i całkując otrzymujemy:

Czy gdzie:

(S-impuls siły)

ponieważ całki po prawej stronie dają impulsy sił zewnętrznych,

równanie (5) wyraża twierdzenie o zmianie pędu układu w postaci całkowej: zmiana pędu układu w pewnym okresie czasu jest równa sumie impulsów sił zewnętrznych działających na układ w tym samym czasie.

W rzutach na osie współrzędnych będziemy mieli:

Prawo zachowania pędu

Z twierdzenia o zmianie pędu układu można wyciągnąć następujące ważne wnioski:

1. Niech suma wszystkich sił zewnętrznych działających na układ będzie równa zero:

Zatem z równania (4) wynika, że w tym przypadku Q = stała

Zatem, jeśli suma wszystkich sił zewnętrznych działających na układ jest równa zeru, wówczas wektor pędu układu będzie stały pod względem wielkości i kierunku.

2. 01Niech siły zewnętrzne działające na układ będą takie, że suma ich rzutów na jakąś oś (np. Ox) będzie równa zeru:

Zatem z równań (4`) wynika, że w tym przypadku Q = stała

Zatem, jeżeli suma rzutów wszystkich działających sił zewnętrznych na dowolną oś jest równa zeru, to rzut wielkości ruchu układu na tę oś jest wartością stałą.

Te wyniki wyrażają prawo zachowania pędu układu. Wynika z nich, że siły wewnętrzne nie mogą zmienić całkowitej wielkości ruchu układu.

Spójrzmy na kilka przykładów:

· Zjawisko powrotu rolki. Jeśli potraktujemy karabin i kulę jako jeden układ, wówczas ciśnienie gazów proszkowych podczas strzału będzie siłą wewnętrzną. Siła ta nie może zmienić całkowitego pędu układu. Ponieważ jednak gazy prochowe, działając na kulę, nadają jej pewien ruch skierowany do przodu, muszą jednocześnie nadać karabinowi taki sam ruch w przeciwnym kierunku. Spowoduje to cofnięcie się karabinu, tj. tzw powrót. Podobne zjawisko występuje podczas strzelania z broni (cofanie).

· Działanie śmigła (śmigła). Śmigło wprawia w ruch pewną masę powietrza (lub wody) wzdłuż osi śmigła, odrzucając tę masę z powrotem. Jeżeli potraktujemy masę rzuconą i samolot (lub statek) jako jeden układ, wówczas siły oddziaływania śmigła z otoczeniem, jako siły wewnętrzne, nie są w stanie zmienić całkowitej wielkości ruchu tego układu. Dlatego też, gdy masa powietrza (wody) zostanie odrzucona, samolot (lub statek) uzyskuje odpowiednią prędkość do przodu, taką, że całkowity ruch rozważanego układu pozostaje równy zeru, ponieważ był zerowy przed rozpoczęciem ruchu .

Podobny efekt uzyskuje się poprzez działanie wioseł lub kół łopatkowych.

· Napęd rekt iwny W rakiecie (rakietie) gazowe produkty spalania paliwa wyrzucane są z dużą prędkością przez otwór w ogonie rakiety (z dyszy silnika odrzutowego). Siły ciśnienia działające w tym przypadku będą siłami wewnętrznymi i nie mogą zmienić całkowitego pędu układu gazy rakietowo-proszkowe. Ponieważ jednak uciekające gazy mają pewien ruch skierowany do tyłu, rakieta otrzymuje odpowiednią prędkość do przodu.

Twierdzenie o momentach względem osi.

Rozważ materialny punkt masy M, poruszając się pod wpływem siły F. Znajdźmy dla niego zależność pomiędzy momentami wektorów mV I F względem pewnej ustalonej osi Z.

m z (F) = xF - yF (7)

Podobnie dla wartości m(mV), jeśli zostanie wyjęty M będzie poza nawiasami

M z (mV) = m(xV - yV)(7`)

Biorąc pochodne po czasie z obu stron tej równości, znajdujemy

Po prawej stronie wynikowego wyrażenia pierwszy nawias jest równy 0, ponieważ dx/dt=V i dу/dt = V, drugi nawias według wzoru (7) jest równy

mz(F), gdyż zgodnie z podstawową zasadą dynamiki:

Wreszcie będziemy mieli (8)

Otrzymane równanie wyraża twierdzenie o momentach wokół osi: pochodna czasowa momentu pędu punktu względem dowolnej osi jest równa momentowi działającej siły względem tej samej osi. Podobne twierdzenie obowiązuje dla chwil wokół dowolnego środka O.

Twierdzenie o zmianie pędu punktu

Ponieważ masa punktu jest stała, a jego przyspieszenie jest stałe, równanie wyrażające podstawową zasadę dynamiki można przedstawić w postaci

Równanie wyraża jednocześnie twierdzenie o zmianie pędu punktu w postaci różniczkowej: pochodna czasu pęd punktu jest równy sumie geometrycznej sił działających na ten punkt.

Całkujmy to równanie. Niech masa będzie punktowana M, poruszający się pod wpływem siły (ryc. 15), ma w tej chwili T=0 prędkości i w tej chwili T 1-biegowa.

Ryc.15

Pomnóżmy zatem obie strony równości i wyjmijmy z nich całki oznaczone. W tym przypadku po prawej stronie, gdzie całkowanie zachodzi w czasie, granice całek będą wynosić 0 i T 1, a po lewej stronie, gdzie prędkość jest zintegrowana, granicami całki będą odpowiednie wartości prędkości i . Ponieważ całka z równa się , wówczas w rezultacie otrzymujemy:

Całki po prawej stronie reprezentują impulsy działających sił. Dlatego ostatecznie będziemy mieli:

Równanie wyraża twierdzenie o zmianie pędu punktu w postaci końcowej: zmiana pędu punktu w pewnym okresie czasu jest równa sumie geometrycznej impulsów wszystkich sił działających na punkt w tym samym okresie czasu ( Ryż. 15).

Podczas rozwiązywania problemów często stosuje się równania w rzutach zamiast równań wektorowych.

W przypadku ruchu prostoliniowego występującego wzdłuż osi Oh twierdzenie wyraża pierwsze z tych równań.

Przykład 9. Znajdź prawo ruchu materialnego punktu masy M, poruszając się wzdłuż osi X pod wpływem stałego modułu siły F(Rys. 16) w warunkach początkowych: , przy .

Ryc.16

Rozwiązanie. Utwórzmy równanie różniczkowe ruchu punktu w rzucie na oś X: . Całkując to równanie, znajdujemy: . Stała jest wyznaczana z warunku początkowego prędkości i wynosi . Wreszcie

Ponadto, biorąc pod uwagę, że v = dx/dt, dochodzimy do równania różniczkowego: , całkując które otrzymujemy

Stałą wyznacza się z warunku początkowego współrzędnej punktu. To jest równe. W związku z tym prawo ruchu punktu ma postać

Przykład 10. Obciążenie ciężarem R(ryc. 17) zaczyna poruszać się od spoczynku wzdłuż gładkiej płaszczyzny poziomej pod wpływem siły F = kt. Znajdź prawo ruchu ładunku.

Ryc.17

Rozwiązanie. Wybierzmy początek układu współrzędnych O w początkowej pozycji obciążenia i skierować oś X w kierunku ruchu (ryc. 17). Wtedy warunki początkowe mają postać: X(t = 0) = 0,v( t = 0) = 0. Na obciążenie działają siły F,P i płaska siła reakcji N. Rzuty tych sił na oś X mają znaczenia FX = F = kt, RX = 0, Nx= 0, zatem odpowiednie równanie ruchu można zapisać następująco: . Rozdzielając zmienne w tym równaniu różniczkowym, a następnie całkując, otrzymujemy: v = Gkt 2 /2P + C 1. Zastępując dane początkowe ( w(0) = 0), stwierdzamy, że C 1 = 0 i otrzymujemy prawo zmiany prędkości .

Ostatnie wyrażenie jest z kolei równaniem różniczkowym, całkując które znajdujemy prawo ruchu punktu materialnego: . Zawarta tutaj stała jest wyznaczana na podstawie drugiego warunku początkowego X(0) = 0. Łatwo to sprawdzić. Wreszcie

Przykład 11. Na ładunku spoczywającym na poziomej gładkiej płaszczyźnie (patrz ryc. 17) w pewnej odległości A od początku zaczyna działać w dodatnim kierunku osi X siła F = k 2 (P/G)X, Gdzie R - waga ładunku. Znajdź prawo ruchu ładunku.

Rozwiązanie. Równanie ruchu rozważanego obciążenia (punktu materialnego) w rzucie na oś X

Warunki początkowe równania (1) mają postać: X(t = 0) = A, v( t = 0) = 0.

Przedstawmy pochodną czasu prędkości zawartej w równaniu (1) następująco:

Podstawiając to wyrażenie do równania (1) i redukując przez ( P/G), otrzymujemy

Oddzielając zmienne w ostatnim równaniu, stwierdzamy, że . Całkując to drugie, mamy: . Stosowanie warunków początkowych , otrzymujemy , a zatem

, . (2)

Ponieważ siła działa na obciążenie w dodatnim kierunku osi X, to jasne jest, że powinien podążać w tym samym kierunku. Dlatego w rozwiązaniu (2) należy wybrać znak plus. Zastępując dalej w drugim wyrażeniu (2) przez , otrzymujemy równanie różniczkowe do określenia prawa ruchu ładunku. Skąd, oddzielając zmienne, mamy

Całkując to drugie, otrzymujemy: . Po znalezieniu stałej w końcu otrzymujemy

Przykład 12. Piłka M szerokie rzesze M(Rys. 18) spada bez prędkości początkowej pod wpływem grawitacji. Kiedy piłka spada, napotyka opór, gdzie – stały współczynnik oporu. Znajdź prawo ruchu piłki.

Ryc.18

Rozwiązanie. Wprowadźmy układ współrzędnych, którego początek będzie znajdował się w punkcie, w którym znajduje się kula t = 0, kierując oś Na pionowo w dół (ryc. 18). Równanie różniczkowe ruchu kuli w rzucie na oś Na ma wtedy formę

Warunki początkowe dla kuli zapisuje się w następujący sposób: y(t = 0) = 0, v( t = 0) = 0.

Rozdzielanie zmiennych w równaniu (1)

i całkując, znajdujemy: , gdzie . Lub po znalezieniu stałej

Lub . (2)

Wynika z tego, że prędkość maksymalna, tj. prędkość w , jest równa .

Aby znaleźć zasadę ruchu, zamień v w równaniu (2) na dy/dt. Następnie całkując powstałe równanie z uwzględnieniem warunku początkowego, w końcu znajdujemy

Przykład 13.Łódź podwodna badawcza o kulistym kształcie i masie M= = 1,5×10 5 kg zaczyna nurkować z wyłączonymi silnikami, mając prędkość poziomą v X 0 = 30 SM i ujemną pływalność R 1 = 0.01mg, Gdzie – suma wektorowa siły wyporu Archimedesa Q i grawitacja mg, działając na łódź (ryc. 20). Siła oporu wody , kg/s. Wyznacz równania ruchu łodzi i jej trajektorię.

Ponieważ masa punktu jest stała, a jego przyspieszenie jest stałe, równanie wyrażające podstawową zasadę dynamiki można przedstawić w postaci

Równanie wyraża jednocześnie twierdzenie o zmianie pędu punktu w postaci różniczkowej: pochodna czasu pęd punktu jest równy sumie geometrycznej sił działających na ten punkt.

Całkujmy to równanie. Niech masa będzie punktowana M, poruszający się pod wpływem siły (ryc. 15), ma w tej chwili T=0 prędkości i w tej chwili T 1-biegowa.

Ryc.15

Całki po prawej stronie reprezentują impulsy działających sił. Dlatego ostatecznie będziemy mieli:

Podczas rozwiązywania problemów często stosuje się równania w rzutach zamiast równań wektorowych.

W przypadku ruchu prostoliniowego występującego wzdłuż osi Oh twierdzenie wyraża pierwsze z tych równań.

Pytania autotestowe

Formułować podstawowe prawa mechaniki.

Jakie równanie nazywa się podstawowym równaniem dynamiki?

Jaka jest miara bezwładności ciał stałych podczas ruchu postępowego?

Czy masa ciała zależy od jego położenia na Ziemi?

Jaki układ odniesienia nazywa się inercyjnym?

Do jakiego ciała przyłożona jest siła bezwładności punktu materialnego oraz jaki jest jej moduł i kierunek?

Wyjaśnij różnicę między pojęciami „bezwładność” i „siła bezwładności”?

Do jakich ciał przykładana jest siła bezwładności, jak jest skierowana i według jakiego wzoru można ją obliczyć?

Jaka jest zasada kinetostatyki?

Jakie są moduły i kierunki stycznych i normalnych sił bezwładności punktu materialnego?

Jak nazywa się masa ciała? Jaka jest jednostka masy w układzie SI?

Jaka jest miara bezwładności ciała?

Zapisz podstawowe zasady dynamiki w postaci wektorowej i różniczkowej?

Na punkt materialny działa stała siła. Jak porusza się punkt?

Jakie przyspieszenie uzyska punkt, jeśli zadziała na niego siła dwukrotnie większa od siły ciężkości?

Po zderzeniu dwóch punktów materialnych z masami M 1 = 6 kg i M 2 = 24 kg pierwszy punkt otrzymał przyspieszenie 1,6 m/s. Jakie przyspieszenie uzyska drugi punkt?

Przy jakim ruchu punktu materialnego jego styczna siła bezwładności jest równa zeru, a przy jakim ruchu jest normalna?

Z jakich wzorów oblicza się moduły sił obrotowych i odśrodkowych bezwładności punktu należącego do ciała sztywnego obracającego się wokół ustalonej osi?

Jak sformułowane jest podstawowe prawo dynamiki punktowej?

Podaj sformułowanie prawa niezależności działania sił.

Zapisz równania różniczkowe ruchu punktu materialnego w postaci wektora i współrzędnych.

Sformułuj istotę pierwszego i drugiego głównego problemu dynamiki punktowej.

Podaj warunki, z których wyznaczane są stałe całkowania różniczkowych równań ruchu punktu materialnego.

Jakie równania dynamiki nazywane są naturalnymi równaniami ruchu punktu materialnego?

Jakie są dwa główne problemy dynamiki punktów, które można rozwiązać za pomocą ruchów różnicowych punktu materialnego?

Równania różniczkowe ruchu swobodnego punktu materialnego.

Jak wyznacza się stałe podczas całkowania różniczkowych równań ruchu punktu materialnego?

Wyznaczanie wartości dowolnych stałych pojawiających się podczas całkowania równań różniczkowych ruchu punktu materialnego.

Jakie są prawa swobodnego spadania ciał?

Według jakich praw zachodzą poziome i pionowe ruchy ciała rzuconego w przestrzeni pod kątem do horyzontu? Jaka jest trajektoria jego ruchu i pod jakim kątem ciało ma największy zasięg lotu?

Jak obliczyć impuls zmiennej siły w skończonym okresie czasu?

Jak nazywa się pęd punktu materialnego?

Jak wyrazić elementarną pracę siły poprzez elementarną drogę punktu przyłożenia siły i jak poprzez przyrost współrzędnej łukowej tego punktu?

Przy jakich przemieszczeniach praca grawitacji jest: a) dodatnia, b) ujemna, c) zerowa?

Jak obliczyć moc siły przyłożonej do punktu materialnego obracającego się wokół ustalonej osi z prędkością kątową?

Sformułuj twierdzenie o zmianie pędu punktu materialnego.

W jakich warunkach pęd punktu materialnego się nie zmienia? W jakich warunkach jego rzut na określoną oś nie zmienia się?

Podaj sformułowanie twierdzenia o zmianie energii kinetycznej punktu materialnego w postaci różniczkowej i skończonej.

Jak nazywa się moment pędu punktu materialnego względem: a) środka, b) osi?

Jak formułuje się twierdzenie o zmianie momentu pędu punktu względem środka i względem osi?

W jakich warunkach moment pędu punktu względem osi pozostaje niezmieniony?

Jak wyznacza się moment pędu punktu materialnego względem środka i względem osi? Jaki jest związek między nimi?

W jakim położeniu wektora pędu punktu materialnego jego moment względem osi jest równy zero?

Dlaczego trajektoria punktu materialnego poruszającego się pod wpływem siły centralnej leży w tej samej płaszczyźnie?

Jaki ruch punktu nazywamy prostoliniowym? Zapisz równanie różniczkowe ruchu prostoliniowego punktu materialnego.

Zapisz równania różniczkowe ruchu płaskiego punktu materialnego.

Jaki ruch punktu materialnego opisują równania różniczkowe Lagrange'a pierwszego rodzaju?

W jakich przypadkach punkt materialny nazywa się nieswobodnym i jakie są równania różniczkowe ruchu tego punktu?

Podaj definicje połączeń stacjonarnych i niestacjonarnych, holonomicznych i nieholonomicznych.

Jakie rodzaje połączeń nazywamy dwustronnymi? Jednostronny?

Jaka jest istota zasady wyzwolenia z więzów?

Jaką postać mają równania różniczkowe ruchu nieswobodnego punktu materialnego w postaci Lagrange'a? Co nazywa się mnożnikiem Lagrange'a?

Podaj sformułowanie dynamicznego twierdzenia Coriolisa.

Jaka jest istota zasady względności Galileo-Newtona?

Nazwij ruchy, w których siła bezwładności Coriolisa wynosi zero.

Jaki moduł i jaki kierunek ma przeniesienie i siły bezwładności Coriolisa?

Jaka jest różnica między równaniami różniczkowymi ruchu względnego i bezwzględnego punktu materialnego?

Jak określa się przenoszenie i siły bezwładności Coriolisa w różnych przypadkach ruchu przenoszącego?

Jaka jest istota zasady względności mechaniki klasycznej?

Jakie układy odniesienia nazywane są inercyjnymi?

Jaki jest warunek względnego spoczynku punktu materialnego?

W jakich punktach powierzchni Ziemi grawitacja ma największą i najmniejszą wartość?

Co wyjaśnia zbaczanie spadających ciał na wschód?

W jakim kierunku odchyla się ciało rzucone pionowo?

Łyżka jest opuszczana na wał z przyspieszeniem A=4 m/s 2. Ciężar łyżki G=2 kN. Wyznacz siłę naciągu liny podtrzymującej wannę?

Dwa punkty materialne poruszają się po linii prostej ze stałymi prędkościami 10 i 100 m/s. Czy można powiedzieć, że do tych punktów przyłożone są równoważne układy sił?

1) jest to niemożliwe;

Do dwóch punktów materialnych o masach 5 i 15 kg przykładane są jednakowe siły. Porównaj wartości liczbowe przyspieszenia tych punktów?

1) przyspieszenia są takie same;

2) przyspieszenie punktu o masie 15 kg jest trzykrotnie mniejsze niż przyspieszenie punktu o masie 5 kg.

Czy problemy dynamiki można rozwiązać za pomocą równań równowagi?

Niech punkt materialny porusza się pod wpływem siły F. Wymagane jest określenie ruchu tego punktu względem poruszającego się układu Oksyz(patrz ruch złożony punktu materialnego), który porusza się w znany sposób względem układu stacjonarnego O 1 X 1 y 1 z 1 .

Podstawowe równanie dynamiki układu stacjonarnego

Zapiszmy bezwzględne przyspieszenie punktu, korzystając z twierdzenia Coriolisa

Gdzie A abs– przyspieszenie bezwzględne;

A wzgl– przyspieszenie względne;

A uliczka– akceleracja przenośna;

A rdzeń– Przyspieszenie Coriolisa.

Przepiszmy (25) biorąc pod uwagę (26)

Wprowadźmy notację
- przenośna siła bezwładności,
- Siła bezwładności Coriolisa. Wtedy równanie (27) przyjmuje postać

Podstawowe równanie dynamiki do badania ruchu względnego (28) zapisuje się analogicznie jak dla ruchu absolutnego, z tym że do sił działających na punkt należy dodać jedynie przeniesienie i siły bezwładności Coriolisa.

Ogólne twierdzenia o dynamice punktu materialnego

Rozwiązując wiele problemów, możesz użyć gotowych półfabrykatów uzyskanych na podstawie drugiego prawa Newtona. W tej sekcji zestawiono takie metody rozwiązywania problemów.

Twierdzenie o zmianie pędu punktu materialnego

Przedstawmy następujące charakterystyki dynamiczne:

1. Pęd punktu materialnego– wielkość wektora równa iloczynowi masy punktu i jego wektora prędkości

. (29)

2. Impuls siły

Elementarny impuls siły– wielkość wektora równa iloczynowi wektora siły i elementarnego przedziału czasu

(30).

Następnie pełny impuls

. (31)

Na F=stała, którą otrzymujemy S=Ft.

Impuls całkowity w skończonym czasie można obliczyć tylko w dwóch przypadkach, gdy siła działająca na punkt jest stała lub zależy od czasu. W innych przypadkach konieczne jest wyrażenie siły w funkcji czasu.

Równość wymiarów impulsu (29) i pędu (30) pozwala ustalić między nimi związek ilościowy.

Rozważmy ruch punktu materialnego M pod działaniem dowolnej siły F po dowolnej trajektorii.

O U:
. (32)

Rozdzielamy zmienne w (32) i całkujemy

. (33)

W rezultacie, biorąc pod uwagę (31), otrzymujemy

. (34)

Równanie (34) wyraża następujące twierdzenie.

Twierdzenie: Zmiana pędu punktu materialnego w pewnym okresie czasu jest równa impulsowi siły działającej na ten punkt w tym samym przedziale czasu.

Podczas rozwiązywania problemów równanie (34) należy rzutować na osie współrzędnych

Twierdzenie to jest wygodne w użyciu, gdy wśród danych i nieznanych wielkości znajduje się masa punktu, jego prędkość początkowa i końcowa, siły i czas ruchu.

Twierdzenie o zmianie momentu pędu punktu materialnego

M
moment pędu punktu materialnego względem środka jest równy iloczynowi modułu pędu punktu i ramienia, tj. najkrótsza odległość (prostopadła) od środka do linii pokrywającej się z wektorem prędkości

, (36)

. (37)

Związek między momentem siły (przyczyną) a momentem pędu (skutkiem) ustala następujące twierdzenie.

Niech punkt M danej masy M porusza się pod wpływem siły F.

,
,

, (38)

. (39)

Obliczmy pochodną (39)

. (40)

Łącząc (40) i (38) ostatecznie otrzymujemy

. (41)

Równanie (41) wyraża następujące twierdzenie.

Twierdzenie: Pochodna po czasie wektora pędu punktu materialnego względem jakiegoś środka jest równa momentowi siły działającej na punkt względem tego samego środka.

Podczas rozwiązywania problemów równanie (41) należy rzutować na osie współrzędnych

W równaniach (42) momenty pędu i siły obliczane są względem osi współrzędnych.

Z (41) wynika prawo zachowania momentu pędu (prawo Keplera).

Jeżeli moment siły działający na punkt materialny względem dowolnego środka wynosi zero, wówczas moment pędu punktu względem tego środka zachowuje swoją wielkość i kierunek.

Jeśli
, To
.