Całkowanie funkcji trygonometrycznych: metody i przykłady. Całkowanie funkcji trygonometrycznych: metody i przykłady Całka iloczynu sinusów

Całki funkcji trygonometrycznych.
Przykłady rozwiązań

W tej lekcji rozważymy całki funkcji trygonometrycznych, to znaczy wypełnienie całek będą sinusami, cosinusami, stycznymi i cotangensami w różnych kombinacjach. Wszystkie przykłady zostaną szczegółowo przeanalizowane, dostępne i zrozumiałe nawet dla czajnika.

Aby pomyślnie studiować całki funkcji trygonometrycznych, musisz być dobrze zorientowany w najprostszych całkach, a także opanować kilka technik całkowania. Z materiałami tymi można zapoznać się na wykładach. Całka nieoznaczona. Przykłady rozwiązań I .

A teraz potrzebujemy: Tablica całek, Tabela pochodna I Podręcznik wzorów trygonometrycznych. Wszystkie instrukcje można znaleźć na stronie Wzory i tablice matematyczne. Polecam drukowanie wszystkiego. Szczególnie skupiam się na wzorach trygonometrycznych, powinny być przed twoimi oczami– bez niej wydajność pracy odczuwalnie spadnie.

Ale najpierw o tym, które całki w tym artykule NIE. Tutaj nie ma całek postaci , - cosinus, sinus pomnożony przez jakiś wielomian (rzadziej coś ze styczną lub cotangensem). Takie całki są całkowane przez części, a aby poznać metodę, przejdź do lekcji Całkowanie przez części. Przykłady rozwiązań Nie ma też całek z "łukami" - arcus tangens, arcus sinus itp., są też najczęściej całkowane przez części.

Podczas znajdowania całek funkcji trygonometrycznych stosuje się szereg metod:

(4) Użyj wzoru tabelarycznego , jedyna różnica polega na tym, że zamiast „x” mamy złożone wyrażenie.

Przykład 2

Przykład 3

Znajdź całkę nieoznaczoną.

Klasyka gatunku dla tych, którzy toną w rankingach. Jak zapewne zauważyłeś, w tablicy całek nie ma całki ze stycznej i cotangensa, ale mimo wszystko takie całki można znaleźć.

(1) Korzystamy ze wzoru trygonometrycznego

(2) Podnosimy funkcję pod znak różniczki.

(3) Użyj całki tabelarycznej .

Przykład 4

Znajdź całkę nieoznaczoną.

To jest przykład samodzielnego rozwiązania, pełne rozwiązanie i odpowiedź znajdują się na końcu lekcji.

Przykład 5

Znajdź całkę nieoznaczoną.

Nasze poziomy będą stopniowo wzrastać =).
Najpierw rozwiązanie:

(1) Korzystamy ze wzoru

(2) Używamy podstawowej tożsamości trygonometrycznej , z czego wynika, że .

(3) Podziel licznik przez mianownik wyraz po wyrazie.

(4) Korzystamy z własności liniowości całki nieoznaczonej.

(5) Całkujemy korzystając z tabeli.

Przykład 6

Znajdź całkę nieoznaczoną.

To jest przykład samodzielnego rozwiązania, pełne rozwiązanie i odpowiedź znajdują się na końcu lekcji.

Istnieją również całki ze stycznych i cotangensów, które są w wyższych potęgach. W lekcji omówiono całkę ze stycznej w sześcianie Jak obliczyć pole figury płaskiej? Całki tangensa (cotangensa) w czwartej i piątej potędze można znaleźć na stronie Całki zespolone.

Zmniejszanie stopnia całki

Ta technika działa, gdy całki są wypełnione sinusami i cosinusami nawet stopni. W celu zmniejszenia stopnia stosuje się wzory trygonometryczne , i , a ostatnia formuła jest częściej używana w przeciwnym kierunku: .

Przykład 7

Znajdź całkę nieoznaczoną.

Rozwiązanie:

W zasadzie nie ma tu nic nowego poza tym, że zastosowaliśmy formułę (obniżenie stopnia całki). Proszę zauważyć, że skróciłem rozwiązanie. W miarę zdobywania doświadczenia całkę z można znaleźć ustnie, co oszczędza czas i jest całkiem do zaakceptowania przy kończeniu zadań. W takim przypadku wskazane jest, aby nie pisać reguły , najpierw ustnie bierzemy całkę z 1, potem - z .

Przykład 8

Znajdź całkę nieoznaczoną.

To jest przykład samodzielnego rozwiązania, pełne rozwiązanie i odpowiedź znajdują się na końcu lekcji.

Obiecany wzrost stopnia:

Przykład 9

Znajdź całkę nieoznaczoną.

Najpierw rozwiązanie, później komentarze:

(1) Przygotuj całkę do zastosowania wzoru .

(2) W rzeczywistości stosujemy formułę.

(3) Podnosimy mianownik do kwadratu i usuwamy stałą ze znaku całki. Można to zrobić trochę inaczej, ale moim zdaniem tak jest wygodniej.

(4) Korzystamy ze wzoru

(5) W trzecim semestrze ponownie obniżamy stopień, ale korzystając ze wzoru .

(6) Podajemy podobne terminy (tutaj podzieliłem termin na termin i dodałem).

(7) W rzeczywistości bierzemy całkę, regułę liniowości a sposób sprowadzenia funkcji pod znak różniczki odbywa się ustnie.

(8) Przeczesujemy odpowiedź.

! W całce nieoznaczonej odpowiedź często można zapisać na kilka sposobów.

W rozważanym właśnie przykładzie ostateczna odpowiedź mogłaby być zapisana inaczej - otwórz nawiasy, a nawet zrób to przed całkowaniem wyrażenia, to znaczy następujące zakończenie przykładu jest całkiem do przyjęcia:

Możliwe, że ta opcja jest jeszcze wygodniejsza, po prostu wyjaśniłem to tak, jak sam decydowałem). Oto kolejny typowy przykład niezależnego rozwiązania:

Przykład 10

Znajdź całkę nieoznaczoną.

Ten przykład został rozwiązany na dwa sposoby i można go uzyskać dwie zupełnie różne odpowiedzi.(dokładniej będą wyglądać zupełnie inaczej, ale z matematycznego punktu widzenia będą równoważne). Najprawdopodobniej nie zobaczysz najbardziej racjonalnego sposobu i będziesz cierpieć z otwieraniem nawiasów przy użyciu innych wzorów trygonometrycznych. Najskuteczniejsze rozwiązanie podano na końcu lekcji.

Podsumowując akapit, dochodzimy do wniosku, że dowolna całka formy , gdzie i - nawet liczbę, rozwiązuje się obniżając stopień całki.
W praktyce spotkałem całki o 8 i 10 stopniach, musiałem rozwiązać ich straszne hemoroidy poprzez kilkukrotne obniżenie stopnia, co skutkowało długimi, długimi odpowiedziami.

Zmienna metoda wymiany

Jak wspomniano w artykule Metoda zmiany zmiennej w całce nieoznaczonej, głównym warunkiem zastosowania metody zastępczej jest fakt, że całka zawiera pewną funkcję i jej pochodną:
(funkcje niekoniecznie są w produkcie)

Przykład 11

Znajdź całkę nieoznaczoną.

Patrzymy na tabelę pochodnych i zauważamy wzory, , czyli w naszej całce jest funkcja i jej pochodna. Widzimy jednak, że podczas różniczkowania cosinus i sinus wzajemnie się przekształcają i powstaje pytanie: jak dokonać zamiany zmiennej i na co ją wyznaczyć - sinus czy cosinus?! Problem można rozwiązać metodą naukowego szturchania: jeśli dokonamy wymiany nieprawidłowo, to nic dobrego z tego nie wyniknie.

Ogólna wskazówka: w podobnych przypadkach należy oznaczyć funkcję znajdującą się w mianowniku.

Przerywamy rozwiązanie i przeprowadzamy wymianę

W mianowniku wszystko jest u nas w porządku, wszystko zależy tylko od , teraz pozostaje dowiedzieć się, w co się to zmieni.
Aby to zrobić, znajdujemy różnicę:

Lub w skrócie:
Z powstałej równości, zgodnie z zasadą proporcji, wyrażamy potrzebne wyrażenie:

Więc:

Teraz cała całka zależy tylko od rozwiązania i możemy kontynuować

Gotowy. Przypominam, że celem zamiany jest uproszczenie całki, w tym przypadku wszystko sprowadza się do całkowania funkcji potęgowej po stole.

To nie przypadek, że tak szczegółowo namalowałem ten przykład, zrobiono to w celu powtórzenia i utrwalenia materiałów lekcyjnych. Metoda zmiany zmiennej w całce nieoznaczonej.

A teraz dwa przykłady niezależnego rozwiązania:

Przykład 12

Znajdź całkę nieoznaczoną.

Przykład 13

Znajdź całkę nieoznaczoną.

Uzupełnij rozwiązania i odpowiedzi na końcu lekcji.

Przykład 14

Znajdź całkę nieoznaczoną.

Tu znowu w całce jest sinus z cosinusem (funkcja z pochodną), ale już w iloczynie i pojawia się dylemat - co oznaczać, sinus czy cosinus?

Możesz spróbować dokonać wymiany za pomocą naukowej metody szturchania, a jeśli nic nie działa, wyznacz ją jako inną funkcję, ale jest:

Ogólna wskazówka: musisz wyznaczyć funkcję, która, mówiąc obrazowo, znajduje się w „niewygodnej pozycji”.

Widzimy, że w tym przykładzie cosinus ucznia „cierpi” z powodu stopnia, a sinus siedzi tak swobodnie, sam.

Dokonajmy więc zamiany:

Jeśli ktoś ma jeszcze trudności z algorytmem zmiany zmiennej i znalezieniem różniczki, to powinien wrócić do lekcji Metoda zmiany zmiennej w całce nieoznaczonej.

Przykład 15

Znajdź całkę nieoznaczoną.

Analizujemy całkę, co powinno być oznaczone przez ?
Rzućmy okiem na nasze wytyczne:
1) Funkcja najprawdopodobniej jest w mianowniku;
2) Funkcja znajduje się w „niewygodnej pozycji”.

Nawiasem mówiąc, te wskazówki dotyczą nie tylko funkcji trygonometrycznych.

W obu kryteriach (zwłaszcza w drugim) sinus pasuje, więc wymiana sama się sugeruje. W zasadzie wymianę można już przeprowadzić, ale najpierw dobrze byłoby wymyślić, z czym zrobić? Najpierw „odpinamy” jeden cosinus:

Rezerwujemy dla naszego „przyszłego” dyferencjału

I wyrażamy przez sinus, używając podstawowej tożsamości trygonometrycznej:

Teraz zamiennik:

Ogólna zasada: jeśli w całce występuje jedna z funkcji trygonometrycznych (sinus lub cosinus). dziwne stopień, to musisz „odgryźć” jedną funkcję od nieparzystego stopnia i wyznaczyć inną funkcję za nią. Mówimy tylko o całkach, gdzie są cosinusy i sinusy.

W rozważanym przykładzie mieliśmy cosinus w nieparzystym stopniu, więc odjęliśmy jeden cosinus od stopnia i oznaczyliśmy sinus.

Przykład 16

Znajdź całkę nieoznaczoną.

Poziomy rosną =).
To jest przykład zrób to sam. Pełne rozwiązanie i odpowiedź na końcu lekcji.

Uniwersalne podstawienie trygonometryczne

Powszechnym przypadkiem zmiany metody zmiennych jest uniwersalne podstawienie trygonometryczne. Możesz spróbować go zastosować, gdy „nie wiesz, co robić”. Ale w rzeczywistości istnieją pewne wytyczne dotyczące jego stosowania. Typowe całki, w których należy zastosować uniwersalne podstawienie trygonometryczne, to następujące całki: , , , itp.

Przykład 17

Znajdź całkę nieoznaczoną.

Uniwersalne podstawienie trygonometryczne w tym przypadku jest realizowane w następujący sposób. Zamieńmy: . Nie używam litery , ale litery , to nie jest jakaś reguła, po prostu jestem przyzwyczajony do decydowania.

Tutaj wygodniej jest znaleźć różnicę, w tym celu z równości wyrażam:
Wiszę na obu częściach łuku stycznego:

Arcus tangens i tangens znoszą się wzajemnie:

Zatem:

W praktyce nie można malować tak szczegółowo, ale po prostu użyć gotowego wyniku:

! Wyrażenie jest ważne tylko wtedy, gdy pod sinusami i cosinusami mamy po prostu „xes” dla całki (o czym porozmawiamy później) wszystko będzie trochę inne!

Zastępując sinusy i cosinusy, zamieniamy się w następujące ułamki:
, , równości te oparte są na dobrze znanych wzorach trygonometrycznych: ,

Czyszczenie może więc wyglądać tak:

Przeprowadźmy uniwersalne podstawienie trygonometryczne:

Aby scałkować funkcje wymierne postaci R(sin x, cos x), stosuje się podstawienie, które nazywa się uniwersalnym podstawieniem trygonometrycznym. Następnie . Uniwersalne podstawienie trygonometryczne często skutkuje dużymi obliczeniami. Dlatego, jeśli to możliwe, stosuj następujące podstawienia.

Całkowanie funkcji racjonalnie zależnych od funkcji trygonometrycznych

1. Całki postaci ∫ sin n xdx , ∫ cos n xdx , n>0
a) Jeżeli n jest nieparzyste, to jedną potęgę sinx (lub cosx) należy umieścić pod znakiem różniczki, az pozostałej potęgi parzystej przejść do funkcji przeciwnej.
b) Jeśli n jest parzyste, to używamy wzorów redukcji
2. Całki postaci ∫ tg n xdx , ∫ ctg n xdx , gdzie n jest liczbą całkowitą.
Formuły muszą być używane

3. Całki postaci ∫ sin n x cos m x dx
a) Niech m i n będą miały różną parzystość. Stosujemy podstawienie t=sin x, jeśli n jest nieparzyste, lub t=cos x, jeśli m jest nieparzyste.
b) Jeśli m i n są parzyste, to używamy wzorów redukcji
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Całki postaci

Jeśli liczby m i n mają tę samą parzystość, wówczas używamy podstawienia t=tg x . Często wygodnie jest zastosować technikę jednostki trygonometrycznej.
5. ∫ grzech(nx) sałata(mx)dx , ∫ sałata(mx) sałata(nx)dx , ∫ grzech(mx) grzech(nx)dx

Użyjmy wzorów do przeliczenia iloczynu funkcji trygonometrycznych na ich sumę:

grzech α cos β = ½(sin(α+β)+sin(α-β))
sałata α sałata β = ½(cos(α+β)+cos(α-β))
grzech α grzech β = ½(cos(α-β)-cos(α+β))

Przykłady
1. Oblicz całkę ∫ cos 4 x sin 3 xdx .
Dokonujemy podstawienia cos(x)=t . Wtedy ∫ cos 4 x grzech 3 xdx =
2. Oblicz całkę.
Dokonując podstawienia sin x=t , otrzymujemy

3. Znajdź całkę.
Dokonujemy zamiany tg(x)=t . Zastępując, otrzymujemy

Całkowanie wyrażeń postaci R(sinx, cosx)

Przykład 1. Oblicz całki:

Rozwiązanie.
a) Całkowanie wyrażeń postaci R(sinx, cosx) , gdzie R jest funkcją wymierną sin x i cos x , zamieniamy na całki funkcji wymiernych za pomocą uniwersalnego podstawienia trygonometrycznego tg(x/2) = t .
Następnie mamy

Uniwersalne podstawienie trygonometryczne umożliwia przejście z całki postaci ∫ R(sinx, cosx) dx na całkę funkcji wymierno-ułamkowej, ale takie podstawienie często prowadzi do nieporęcznych wyrażeń. W pewnych warunkach prostsze podstawienia okazują się skuteczne:

Jeśli równość R(-sin x, cos x) = -R(sin x, cos x)dx jest prawdziwa, to stosowane jest podstawienie cos x = t.
Jeśli R(sin x, -cos x) = -R(sin x, cos x)dx jest prawdziwe, to podstawienie sin x = t .
Jeśli R(-sin x, -cos x) = R(sin x, cos x)dx jest prawdziwe, to podstawienie to tgx = t lub ctg x = t .

W tym przypadku, aby znaleźć całkę

stosujemy uniwersalne podstawienie trygonometryczne tg(x/2) = t .
Następnie odpowiedz:

Przedstawiono podstawowe wzory trygonometryczne i podstawowe podstawienia. Opisano metody całkowania funkcji trygonometrycznych - całkowanie funkcji wymiernych, iloczyn funkcji potęgowych sin x i cos x, iloczyn wielomianu, wykładnika i sinusa lub cosinusa, całkowanie odwrotnych funkcji trygonometrycznych. Dotyczy to niestandardowych metod.

Treść

Standardowe metody całkowania funkcji trygonometrycznych

Ogólne podejście

Najpierw, jeśli to konieczne, całkę należy przekształcić tak, aby funkcje trygonometryczne zależały od jednego argumentu, który pokrywałby się ze zmienną całkową.

Na przykład, jeśli całka zależy od grzech(x+a) I cos(x+b), to powinieneś wykonać transformację:
sałata (x+b) = sałata (x+a - (a-b)) = sałata (x+a) sałata (b-a) + grzech(x+a) grzech(b-a).
Następnie dokonaj zmiany z = x+a . W rezultacie funkcje trygonometryczne będą zależeć tylko od zmiennej całkowej z .

Gdy funkcje trygonometryczne zależą od jednego argumentu, pokrywającego się ze zmienną całkowania (powiedzmy, że jest to z ), to znaczy całka składa się tylko z funkcji typu grzech Z, bo z, tgz, ctgz, to musisz dokonać zamiany
.
Takie podstawienie prowadzi do całkowania funkcji wymiernych lub niewymiernych (jeśli istnieją pierwiastki) i pozwala obliczyć całkę, jeśli jest całkowana w funkcjach elementarnych.

Jednak często można znaleźć inne metody, które pozwalają obliczyć całkę w krótszy sposób, w oparciu o specyfikę całki. Poniżej znajduje się podsumowanie głównych takich metod.

Metody całkowania funkcji wymiernych sin x i cos x

Funkcje wymierne z grzech x I bo x są funkcjami pochodnymi grzech x, bo x oraz dowolne stałe wykorzystujące operacje dodawania, odejmowania, mnożenia, dzielenia i podnoszenia do potęgi całkowitej. Są one oznaczone następująco: R (sinx, cosx). Może to również obejmować styczne i cotangensy, ponieważ są one tworzone przez podzielenie sinusa przez cosinus i odwrotnie.
Całki funkcji wymiernych mają postać:
.

Metody całkowania wymiernych funkcji trygonometrycznych są następujące.
1) Podstawienie zawsze prowadzi do całki ułamka wymiernego. Jednak w niektórych przypadkach istnieją podstawienia (patrz poniżej), które powodują krótsze obliczenia.
2) Jeśli r (sinx, cosx) sałata x → - sałata x grzech x.
3) Jeśli r (sinx, cosx) pomnożona przez -1 przy zastępowaniu grzech x → - grzech x, następnie podstawienie t = bo x.
4) Jeśli R (sinx, cosx) nie zmienia się jak przy jednoczesnej wymianie sałata x → - sałata x, I grzech x → - grzech x, następnie podstawienie t = tg x lub t= KTG x.

Przykłady:
, , .

Iloczyn funkcji potęgowych cos x i sin x

Całki formy

są całkami wymiernych funkcji trygonometrycznych. Dlatego metody opisane w poprzedniej sekcji można do nich zastosować. Poniżej rozważymy metody oparte na specyfice takich całek.

Jeśli m i n są liczbami wymiernymi, to jedna z permutacji t = grzech x lub t= bo x całka redukuje się do całki dwumianu różniczkowego.

Jeżeli m i n są liczbami całkowitymi, to całkowanie odbywa się za pomocą wzorów redukcyjnych:

;
;
;
.

Przykład:
.

Całki z iloczynu wielomianu i sinusa lub cosinusa

Całki postaci:
, ,
gdzie P(x) jest wielomianem w x są całkowane przez części. Powoduje to następujące formuły:

;
.

Przykłady:
, .

Całki z iloczynu wielomianu, wykładnika i sinusa lub cosinusa

Całki postaci:
, ,
gdzie P(x) jest wielomianem w x , są całkowane za pomocą wzoru Eulera
e iax = cos topór + isin topór(gdzie i 2 = - 1 ).
W tym celu metoda opisana w poprzednim akapicie oblicza całkę
.
Po oddzieleniu części rzeczywistej i urojonej od wyniku uzyskuje się oryginalne całki.

Przykład:
.

Niestandardowe metody całkowania funkcji trygonometrycznych

Poniżej przedstawiono szereg niestandardowych metod, które pozwalają wykonać lub uprościć całkowanie funkcji trygonometrycznych.

Zależność od (a grzech x + b cos x)

Jeśli całka zależy tylko od a grzech x + b cos x, warto zastosować wzór:
,
Gdzie .

Na przykład

Rozkład ułamków z sinusów i cosinusów na ułamki prostsze

Rozważ całkę
.
Najprostszym sposobem całkowania jest rozłożenie ułamka na prostsze, stosując przekształcenie:
grzech(a - b) = grzech(x + a - (x + b)) = grzech(x+a) cos(x+b) - cos(x+a) grzech(x+b)

Całkowanie ułamków pierwszego stopnia

Podczas obliczania całki
,
wygodnie jest wybrać część całkowitą ułamka i pochodną mianownika
A 1 grzech x + b 1 sałata x = A (a grzech x + b cos x) + B (a grzech x + b cos x)′ .
Stałe A i B można znaleźć, porównując lewą i prawą stronę.

Bibliografia:
NM Gunther, RO Kuźmin, Zbiór problemów matematyki wyższej, Lan, 2003.

Zobacz też:

Pojawią się również zadania do samodzielnego rozwiązania, na które możecie zobaczyć odpowiedzi.

Całkę można zamienić z iloczynu funkcji trygonometrycznych na sumę

Rozważmy całki, w których całka jest iloczynem sinusów i cosinusów pierwszego stopnia x pomnożonych przez różne czynniki, czyli całki postaci

Korzystanie ze znanych wzorów trygonometrycznych

(2)
(3)
(4)
każdy z iloczynów w całkach postaci (31) można przekształcić w sumę algebraiczną i całkować za pomocą wzorów

(5)

(6)

Przykład 1 Znajdować

Rozwiązanie. Zgodnie ze wzorem (2) o godz

Przykład 2 Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Zgodnie ze wzorem (3) o godz

Przykład 3 Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Zgodnie ze wzorem (4) o godz otrzymujemy następujące przekształcenie całki:

Stosując wzór (6), otrzymujemy

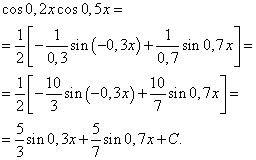
Całka iloczynu potęg sinusa i cosinusa tego samego argumentu

Rozważmy teraz całki funkcji, które są iloczynem potęg sinusa i cosinusa tego samego argumentu, tj.

(7)

W szczególnych przypadkach jeden ze wskaźników ( M Lub N) może wynosić zero.

Podczas całkowania takich funkcji stosuje się, że parzysta moc cosinusa może być wyrażona w postaci sinusa, a różniczka sinusa jest równa cos x dx(lub parzysta potęga sinusa może być wyrażona jako cosinus, a różniczka cosinusa to - sin x dx ) .

Należy rozróżnić dwa przypadki: 1) co najmniej jeden ze wskaźników M I N dziwne; 2) oba wskaźniki są równe.

Załóżmy pierwszy przypadek, a mianowicie wykładnik N = 2k+ 1 - nieparzyste. Następnie, biorąc to pod uwagę

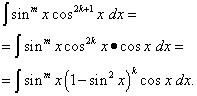
Całka jest przedstawiona w taki sposób, że jedna jej część jest funkcją samego sinusa, a druga różniczką sinusa. Teraz ze zmianą zmiennej T= grzech X rozwiązanie sprowadza się do całkowania wielomianu względem T. Byle tylko stopień M jest nieparzysta, zrób to samo, oddzielając czynnik sin X, wyrażając resztę całki w kategoriach cos X i zakładając T= cos X. Podejście to można również zastosować, gdy całkowanie potęg cząstkowych sinusa i cosinusa , Gdy co najmniej jeden ze wskaźników jest nieparzysty . Cały sens polega na tym iloraz potęg sinusa i cosinusa jest szczególnym przypadkiem ich iloczynu : gdy funkcja trygonometryczna jest w mianowniku całki, jej stopień jest ujemny. Ale są też przypadki cząstkowych funkcji trygonometrycznych, gdy ich stopnie są tylko parzyste. O nich - następny akapit.

Jeśli oba wskaźniki M I N są parzyste, to używając wzorów trygonometrycznych

obniżyć wykładniki sinusa i cosinusa, po czym otrzymamy całkę takiego samego typu jak powyżej. Dlatego integracja powinna być kontynuowana w ten sam sposób. Jeśli jeden z parzystych wskaźników jest ujemny, to znaczy brany jest pod uwagę iloraz parzystych mocy sinusa i cosinusa, to ten schemat nie jest odpowiedni . Następnie stosuje się zmianę zmiennej, w zależności od tego, jak można przekształcić całkę. Taki przypadek zostanie rozpatrzony w następnym rozdziale.

Przykład 4 Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Wykładnik cosinusa jest nieparzysty. Dlatego wyobraź sobie

T= grzech X(Następnie dt= cos X dx ). Wtedy dostajemy

Wracając do starej zmiennej, w końcu znajdujemy

Przykład 5 Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Wykładnik cosinusa, podobnie jak w poprzednim przykładzie, jest nieparzysty, ale większy. Wyobrażać sobie

i dokonać zmiany zmiennej T= grzech X(Następnie dt= cos X dx ). Wtedy dostajemy

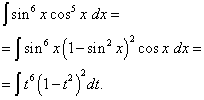
Otwórzmy nawiasy

i dostać

Wracając do starej zmiennej, otrzymujemy rozwiązanie

Przykład 6 Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Wykładniki sinusa i cosinusa są parzyste. Dlatego przekształcamy całkę w następujący sposób:

Wtedy dostajemy

W drugiej całce dokonujemy zmiany zmiennej, nastawy T= grzech2 X. Następnie (1/2)dt= cos2 X dx . Stąd,

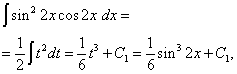
Wreszcie dostajemy

Korzystanie z metody zastępowania zmiennych

Zmienna metoda wymiany przy całkowaniu funkcji trygonometrycznych może być stosowany w przypadkach, gdy w całce występuje tylko sinus lub tylko cosinus, iloczyn sinusa i cosinusa, w którym albo sinus, albo cosinus jest pierwszego stopnia, styczna lub cotangens, a także jako iloraz parzystych potęg sinusa i cosinusa jednego i tego samego argumentu. W tym przypadku możliwe jest wykonanie permutacji nie tylko grzechu X = T i grzech X = T, ale także tg X = T i ktg X = T .

Przykład 8 Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Zmieńmy zmienną: , a następnie . Otrzymaną całkę można łatwo scałkować po tablicy całek:

Przykład 9 Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Zamieńmy tangens na stosunek sinusa i cosinusa:

Zmieńmy zmienną: , a następnie . Wynikowa całka to całka stołowa ze znakiem minus:

Wracając do oryginalnej zmiennej, ostatecznie otrzymujemy:

Przykład 10 Znajdować całka funkcji trygonometrycznej

Rozwiązanie. Zmieńmy zmienną: , a następnie .

Przekształcamy całkę, aby zastosować tożsamość trygonometryczną :

Dokonujemy zmiany zmiennej, nie zapominając o postawieniu znaku minus przed całką (patrz wyżej, co jest równe dt). Następnie rozkładamy całkę na czynniki i całkujemy zgodnie z tabelą:

Wracając do oryginalnej zmiennej, ostatecznie otrzymujemy:

Znajdź samodzielnie całkę funkcji trygonometrycznej, a następnie zobacz rozwiązanie

Uniwersalne podstawienie trygonometryczne

Uniwersalne podstawienie trygonometryczne można użyć w przypadkach, w których całka nie podlega przypadkom omówionym w poprzednich akapitach. Zasadniczo, gdy sinus lub cosinus (lub oba) jest w mianowniku ułamka. Udowodniono, że sinus i cosinus można zastąpić innym wyrażeniem zawierającym tangens połowy pierwotnego kąta w następujący sposób:

Należy jednak pamiętać, że uniwersalne podstawienie trygonometryczne często pociąga za sobą dość złożone przekształcenia algebraiczne, dlatego najlepiej jest go stosować, gdy żadna inna metoda nie działa. Przyjrzyjmy się przykładom, w których wraz z uniwersalnym podstawieniem trygonometrycznym stosuje się podstawienie pod znakiem różniczki i metodę nieokreślonych współczynników.

Przykład 12. Znajdować całka funkcji trygonometrycznej