Równania w Internecie. Sposoby rozwiązywania równań kwadratowych Rozwiąż równanie dla n

Równania kwadratowe.

Równanie kwadratowe- równanie algebraiczne postaci ogólnej

gdzie x jest zmienną wolną,

a, b, c, - współczynniki, i

Wyrażenie zwany trójmianem kwadratowym.

Metody rozwiązywania równań kwadratowych.

1. METODA : Faktoryzacja lewej strony równania.

Rozwiążmy równanie x 2 + 10x - 24 = 0. Rozłóżmy lewą stronę na czynniki:

x 2 + 10x - 24 \u003d x 2 + 12x - 2x - 24 \u003d x (x + 12) - 2 (x + 12) \u003d (x + 12) (x - 2).

Dlatego równanie można zapisać jako:

(x + 12)(x - 2) = 0

Ponieważ iloczyn wynosi zero, to co najmniej jeden z jego czynników wynosi zero. Dlatego lewa strona równania znika w punkcie x = 2, a także o godz x = - 12. Oznacza to, że liczba 2 I - 12 są pierwiastkami równania x 2 + 10x - 24 = 0.

2. METODA : Metoda wyboru pełnego kwadratu.

Rozwiążmy równanie x 2 + 6x - 7 = 0. Zaznaczmy pełny kwadrat po lewej stronie.

Aby to zrobić, piszemy wyrażenie x 2 + 6x w następującej formie:

x 2 + 6 x = x 2 + 2 x 3.

W wynikowym wyrażeniu pierwszy wyraz to kwadrat liczby x, a drugi to podwójny iloczyn x przez 3. Dlatego, aby uzyskać pełny kwadrat, musisz dodać 3 2, ponieważ

x 2+ 2 x 3 + 3 2 \u003d (x + 3) 2.

Przekształcamy teraz lewą stronę równania

x 2 + 6x - 7 = 0,

dodawanie i odejmowanie 3 2 . Mamy:

x 2 + 6x - 7 = x 2+ 2 x 3 + 3 2 - 3 2 - 7 = (x + 3) 2 - 9 - 7 = (x + 3) 2 - 16.

Zatem równanie to można zapisać w następujący sposób:

(x + 3) 2 - 16 = 0, (x + 3) 2 = 16.

Stąd, x + 3 - 4 = 0, x 1 = 1 lub x + 3 = -4, x 2 = -7.

3. METODA :Rozwiązanie równań kwadratowych według wzoru.

Pomnóż obie strony równania

topór 2 + bx + do \u003d 0, za ≠ 0

na 4a i kolejno mamy:

4a 2 x 2 + 4abx + 4ac = 0,

((2ax) 2 + 2ax b + b 2) - b 2 + 4ac \u003d 0,

(2ax + b) 2 = b 2 - 4ac,

2ax + b \u003d ± √ b 2 - 4ac,

2ax \u003d - b ± √ b 2 - 4ac,

Przykłady.

A) Rozwiążmy równanie: 4x2 + 7x + 3 = 0.

a = 4, b = 7, do = 3, re = b 2 - 4 ac = 7 2 - 4 4 3 = 49 - 48 = 1,

D > 0 dwa różne korzenie;

Zatem w przypadku pozytywnego wyróżnika, tj. Na

b2 - 4ac >0, równanie topór 2 + bx + do = 0 ma dwa różne pierwiastki.

B) Rozwiążmy równanie: 4x 2 - 4x + 1 = 0,

a \u003d 4, b \u003d - 4, c \u003d 1, D \u003d b 2 - 4ac \u003d (-4) 2 - 4 4 1= 16 - 16 \u003d 0,

D=0 jeden korzeń;

Tak więc, jeśli dyskryminator jest równy zeru, tj. b 2 - 4ac = 0, następnie równanie

topór 2 + bx + do = 0 ma jeden pierwiastek

V) Rozwiążmy równanie: 2x 2 + 3x + 4 = 0,

a = 2, b = 3, c = 4, re = b 2 - 4ac = 3 2 - 4 2 4 = 9 - 32 = - 13, re< 0.

To równanie nie ma pierwiastków.

Tak więc, jeśli wyróżnik jest ujemny, tj. b2-4ac< 0 , równanie

topór 2 + bx + do = 0 nie ma korzeni.

Wzór (1) pierwiastków równania kwadratowego topór 2 + bx + do = 0 pozwala odnaleźć korzenie każdy równanie kwadratowe (jeśli istnieje), w tym zredukowane i niepełne. Formuła (1) jest wyrażona werbalnie w następujący sposób: pierwiastki równania kwadratowego są równe ułamkowi, którego licznik jest równy drugiemu współczynnikowi, wziętemu z przeciwnym znakiem, plus minus pierwiastek kwadratowy z kwadratu tego współczynnika bez poczwórnego iloczynu pierwszego współczynnika przez wolny wyraz, a mianownik jest dwukrotnością pierwszego współczynnika.

4. METODA: Rozwiązywanie równań z wykorzystaniem twierdzenia Viety.

Jak wiadomo, dane równanie kwadratowe ma postać

x 2 + piks + do = 0.(1)

Jego korzenie spełniają twierdzenie Vieta, które, kiedy =1 ma formę

x 1 x 2 = q,

x 1 + x 2 = - str

Z tego możemy wyciągnąć następujące wnioski (znaki pierwiastków można przewidzieć ze współczynników p i q).

a) Jeżeli skrócony termin Q równania zredukowanego (1) jest dodatnie ( q > 0), to równanie ma dwa pierwiastki tego samego znaku i to jest zazdrość drugiego współczynnika P. Jeśli R< 0 , to oba pierwiastki są ujemne, jeśli R< 0 , to oba pierwiastki są dodatnie.

Na przykład,

x 2 - 3x + 2 = 0; x 1 = 2 I x 2 \u003d 1, ponieważ q = 2 > 0 I p=-3< 0;

x2 + 8x + 7 = 0; x 1 = - 7 I x 2 \u003d - 1, ponieważ q = 7 > 0 I p=8 > 0.

b) Jeśli jesteś wolnym członkiem Q równania zredukowanego (1) jest ujemne ( Q< 0 ), to równanie ma dwa pierwiastki o różnych znakach, a większy pierwiastek w wartości bezwzględnej będzie dodatni, jeśli P< 0 , lub ujemne, jeśli p > 0 .

Na przykład,

x 2 + 4x - 5 = 0; x 1 = - 5 I x 2 \u003d 1, ponieważ q= - 5< 0 I p = 4 > 0;

x 2 - 8x - 9 \u003d 0; x 1 = 9 I x 2 \u003d - 1, ponieważ q = - 9< 0 I p=-8< 0.

Przykłady.

1) Rozwiąż równanie 345x 2 - 137x - 208 = 0.

Rozwiązanie. Ponieważ a + b + c \u003d 0 (345 - 137 - 208 \u003d 0), To

x 1 = 1, x 2 = do / za = -208/345.

Odpowiedź 1; -208/345.

2) Rozwiąż równanie 132x 2 - 247x + 115 = 0.

Rozwiązanie. Ponieważ a + b + c \u003d 0 (132 - 247 + 115 \u003d 0), To

x 1 \u003d 1, x 2 \u003d c / a \u003d 115/132.

Odpowiedź 1; 115/132.

B. Jeśli drugi współczynnik b = 2 tys jest liczbą parzystą, to formuła pierwiastków

Przykład.

Rozwiążmy równanie 3x2 - 14x + 16 = 0.

Rozwiązanie. Mamy: za = 3, b = - 14, do = 16, k = - 7;

D \u003d k 2 - ac \u003d (- 7) 2 - 3 16 \u003d 49 - 48 \u003d 1, D\u003e 0, dwa różne korzenie;

Odpowiedź: 2; 8/3

W. Zredukowane równanie

x 2 + piks + q \u003d 0

pokrywa się z ogólnym równaniem, w którym za = 1, b = str I do = q. Dlatego dla zredukowanego równania kwadratowego wzór na pierwiastki

Przybiera postać:

Formuła (3) jest szczególnie wygodna w użyciu, gdy R- Liczba parzysta.

Przykład. Rozwiążmy równanie x 2 - 14x - 15 = 0.

Rozwiązanie. Mamy: x 1,2 \u003d 7 ±

Odpowiedź: x 1 = 15; x 2 \u003d -1.

5. METODA: Graficzne rozwiązywanie równań.

Przykład. Rozwiąż równanie x2 - 2x - 3 = 0.

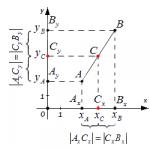
Narysujmy funkcję y \u003d x2 - 2x - 3

1) Mamy: a = 1, b = -2, x0 = 1, y0 = f(1)= 12 - 2 - 3 = -4. Oznacza to, że punkt (1; -4) jest wierzchołkiem paraboli, a prosta x \u003d 1 jest osią paraboli.

2) Weź dwa punkty na osi x, które są symetryczne względem osi paraboli, na przykład punkty x \u003d -1 i x \u003d 3.

Mamy f(-1) = f(3) = 0. Skonstruujmy punkty (-1; 0) i (3; 0) na płaszczyźnie współrzędnych.

3) Przez punkty (-1; 0), (1; -4), (3; 0) rysujemy parabolę (ryc. 68).

Pierwiastkami równania x2 - 2x - 3 = 0 są odcięte punkty przecięcia paraboli z osią x; więc pierwiastki równania to: x1 = - 1, x2 - 3.

Rozwiązanie równania oznacza znalezienie takich wartości niewiadomych, dla których równość będzie prawdziwa.

Rozwiązanie równania

Przedstawmy równanie w następującej postaci:

2x * x - 3 * x = 0.

Widzimy, że wyrazy równania po lewej stronie mają wspólny czynnik x. Wyjmijmy to z nawiasów i napiszmy:

x * (2x - 3) = 0.

Otrzymane wyrażenie jest iloczynem czynników x i (2x - 3). Przypomnijmy, że iloczyn jest równy 0, jeśli przynajmniej jeden z czynników jest równy 0. Możemy więc zapisać równości:

x = 0 lub 2x - 3 = 0.

Zatem jednym z pierwiastków pierwotnego równania jest x 1 = 0.
Znajdź drugi pierwiastek, rozwiązując równanie 2x - 3 = 0.

W tym wyrażeniu 2x to odcięcie, 3 to odejmowanie, a 0 to różnica. Aby znaleźć odcięcie, musisz dodać odejmowanie do różnicy:

W ostatnim wyrażeniu 2 i x to czynniki, 3 to iloczyn. Aby znaleźć nieznany czynnik, musisz podzielić iloczyn przez znany czynnik:

W ten sposób znaleźliśmy drugi pierwiastek równania: x 2 \u003d 1,5.

Sprawdzenie poprawności rozwiązania

Aby dowiedzieć się, czy równanie zostało rozwiązane poprawnie, należy wstawić do niego wartości liczbowe x i wykonać niezbędne operacje arytmetyczne. Jeżeli w wyniku obliczeń okaże się, że lewa i prawa część wyrażenia mają taką samą wartość, to równanie jest rozwiązane poprawnie.

Sprawdźmy:

Obliczmy wartość oryginalnego wyrażenia przy x 1 = 0 i uzyskajmy:

2 * 0 2 - 3 * 0 = 0,

0 = 0, prawda.

Obliczmy wartość wyrażenia przy x 2 = 0 i uzyskajmy:

2 * 1,5 2 - 3 * 1,5 = 0,

2 * 2,25 - 4,5 = 0,

0 = 0, prawda.

Więc równanie jest poprawne.

Odpowiedź: x 1 \u003d 0, x 2 \u003d 1,5.

rozwiązać matematykę. Znajdź szybko rozwiązanie równania matematycznego w trybie online. Strona internetowa www.site pozwala Rozwiązać równanie prawie dowolne algebraiczny, trygonometryczny Lub równanie transcendentalne online. Studiując prawie każdy dział matematyki na różnych etapach, trzeba się zdecydować równania w Internecie. Aby uzyskać natychmiastową odpowiedź, a co najważniejsze dokładną odpowiedź, potrzebujesz zasobu, który Ci to umożliwi. Dzięki www.site rozwiązywać równania online zajmie kilka minut. Główną zaletą www.site przy rozwiązywaniu problemów matematycznych równania w Internecie- jest szybkość i trafność udzielonej odpowiedzi. Witryna jest w stanie rozwiązać każdy równania algebraiczne online, równania trygonometryczne online, równania transcendentalne online, I równania z nieznanymi parametrami w trybie online. równania służyć jako potężny aparat matematyczny rozwiązania zadania praktyczne. Z pomocą równania matematyczne możliwe jest przedstawienie faktów i relacji, które na pierwszy rzut oka mogą wydawać się zagmatwane i złożone. nieznane ilości równania można znaleźć formułując problem w matematyczny język w formie równania I decydować otrzymane zadanie w trybie online na stronie internetowej www.site. Każdy równanie algebraiczne, równanie trygonometryczne Lub równania zawierający nadzmysłowyłatwo Cię rozpoznaje decydować online i uzyskaj właściwą odpowiedź. Studiując nauki przyrodnicze, nieuchronnie napotyka się na potrzebę rozwiązywanie równań. W takim przypadku odpowiedź musi być dokładna i musi zostać odebrana natychmiast w trybie online. Dlatego za rozwiązuj równania matematyczne online polecamy stronę www.site, która stanie się Twoim niezbędnym kalkulatorem rozwiązuj równania algebraiczne online, równania trygonometryczne online, I równania transcendentalne online Lub równania o nieznanych parametrach. Do praktycznych problemów znajdowania korzeni różnych równania matematyczne zasób www.. Rozwiązywanie równania w Internecie samodzielnie, warto sprawdzić otrzymaną odpowiedź za pomocą rozwiązanie równań online na stronie internetowej www.site. Konieczne jest prawidłowe napisanie równania i natychmiastowe uzyskanie rozwiązanie internetowe, po czym pozostaje tylko porównać odpowiedź z rozwiązaniem równania. Sprawdzenie odpowiedzi zajmie nie więcej niż minutę rozwiąż równanie online i porównaj odpowiedzi. Pomoże to uniknąć błędów w decyzja i popraw odpowiedź na czas rozwiązywanie równań online albo algebraiczny, trygonometryczny, niedościgniony Lub równanie o nieznanych parametrach.

W tym artykule nauczymy się rozwiązywać równania dwukwadratowe.

Jakiego rodzaju równania nazywamy dwukwadratowymi?
Wszystko równania postaci hmm 4+ bx 2 + C = 0 , Gdzie a ≠ 0, które są kwadratowe względem x 2 , oraz nazywane są dwukwadratowymi równania. Jak widać, ten wpis jest bardzo podobny do równania kwadratowego, więc równania dwukwadratowe będziemy rozwiązywać za pomocą wzorów, których użyliśmy przy rozwiązywaniu równania kwadratowego.

Tylko będziemy musieli wprowadzić nową zmienną, czyli oznaczamy x2 inna zmienna, np. Na Lub T (lub jakakolwiek inna litera alfabetu łacińskiego).

Na przykład, Rozwiązać równanie x 4 + 4 x 2 - 5 = 0.

Oznaczać x2 Poprzez Na (x 2 = y ) i otrzymać równanie y 2 + 4y - 5 = 0.
Jak widać, wiesz już, jak rozwiązywać takie równania.

Rozwiązujemy wynikowe równanie:

D \u003d 4 2 - 4 (- 5) \u003d 16 + 20 \u003d 36, √ D \u003d √ 36 \u003d 6.

y 1 = (‒ 4 - 6)/2 = - 10 /2 = - 5,

y 2 \u003d (- 4 + 6) / 2 \u003d 2 / 2 \u003d 1.

Wróćmy do naszej zmiennej x.

Mamy to x 2 \u003d - 5 i x 2 \u003d 1.

Zauważmy, że pierwsze równanie nie ma rozwiązań, a drugie daje dwa rozwiązania: x 1 = 1 i x 2 = –1. Uważaj, aby nie zgubić pierwiastka ujemnego (najczęściej dostają odpowiedź x = 1, co nie jest poprawne).

Odpowiedź:- 1 i 1.

Aby lepiej zrozumieć temat, spójrzmy na kilka przykładów.

Przykład 1 Rozwiązać równanie 2x4 - 5x2 + 3 = 0.

Niech x 2 \u003d y, a następnie 2y 2 - 5y + 3 \u003d 0.

re = (‒ 5) 2 - 4 2 3 = 25 - 24 = 1, √ re = √ 1 = 1.

y 1 \u003d (5 - 1) / (2 2) \u003d 4 / 4 \u003d 1, y 2 \u003d (5 + 1) / (2 2) \u003d 6 / 4 \u003d 1,5.

Następnie x 2 \u003d 1 i x 2 \u003d 1,5.

Otrzymujemy x 1 \u003d -1, x 2 \u003d 1, x 3 \u003d - √1,5, x 4 \u003d √1,5.

Odpowiedź: ‒1; 1; ‒ √1,5; √1,5.

Przykład 2 Rozwiązać równanie 2 x 4 + 5 x 2 + 2 = 0.

2y 2 + 5y + 2 = 0.

re = 5 2 - 4 2 2 = 25 - 16 = 9, √ re = √ 9 = 3.

y 1 = (– 5 – 3)/(2 2) = – 8/4 = –2, y 2 = (–5 + 3)/(2 2) = – 2/4 = – 0,5.

Wtedy x 2 = - 2 i x 2 = - 0,5. Zauważ, że żadne z tych równań nie ma rozwiązania.

Odpowiedź: nie ma rozwiązań.

Niepełne równania dwukwadratowe- to kiedy B = 0 (ax 4 + c = 0) albo inaczej C = 0

(ax 4 + bx 2 = 0) są rozwiązywane jak niepełne równania kwadratowe.

Przykład 3 Rozwiązać równanie x 4 - 25 x 2 = 0

Rozkładamy na czynniki, wyjmujemy x 2 z nawiasów, a następnie x 2 (x 2 - 25) = 0.

Otrzymujemy x 2 \u003d 0 lub x 2 - 25 \u003d 0, x 2 \u003d 25.

Wtedy mamy pierwiastki 0; 5 i - 5.

Odpowiedź: 0; 5; – 5.

Przykład 4 Rozwiązać równanie 5x 4 - 45 = 0.

x 2 = - √9 (brak rozwiązań)

x 2 \u003d √ 9, x 1 \u003d - 3, x 2 \u003d 3.

Jak widać, wiedząc, jak rozwiązywać równania kwadratowe, poradzisz sobie z dwukwadratowymi.

Jeśli nadal masz pytania, zapisz się na moje lekcje. Korepetytor Valentina Galinevskaya.

strona, z pełnym lub częściowym kopiowaniem materiału, wymagany jest link do źródła.

Rozwiązać równanie X 2 +(1-x) 2 =x

Udowodnij, że nie ma liczb całkowitych, które zwiększają się pięciokrotnie, przestawiając cyfrę początkową na koniec.

W pewnym królestwie co dwaj są albo przyjaciółmi, albo wrogami. Każdy może w pewnym momencie pokłócić się ze wszystkimi przyjaciółmi i zawrzeć pokój ze wszystkimi wrogami. Okazało się, że co trzy osoby mogą w ten sposób zostać przyjaciółmi. Udowodnij, że wtedy wszyscy ludzie w tym królestwie mogą zostać przyjaciółmi.

W trójkącie jedna ze środkowych jest prostopadła do jednej z dwusiecznych. Udowodnij, że jeden z boków tego trójkąta jest dwa razy większy od drugiego.

Zadania do przeprowadzenia powiatowej (miejskiej) olimpiady dla uczniów z matematyki.

Strzelając z tarczy, zawodnik znokautował tylko 8,9 i 10 punktów. W sumie, oddając ponad 11 strzałów, znokautował dokładnie 100 punktów. Ile strzałów oddał zawodnik i jakie były trafienia?

Udowodnij prawdziwość nierówności:

3. Rozwiąż równanie:

Znajdź liczbę trzycyfrową, która po przekreśleniu środkowej cyfry zmniejsza się 7-krotnie.

W trójkącie ABC poprowadzono dwusieczne z wierzchołków A i B. Następnie z wierzchołka C poprowadzono linie proste równoległe do tych dwusiecznych. Punkty D i E przecięcia tych prostych z dwusiecznymi są połączone. Okazało się, że proste DE i AB są równoległe. Udowodnij, że trójkąt ABC jest równoramienny.

Zadania do przeprowadzenia powiatowej (miejskiej) olimpiady dla uczniów z matematyki.

Rozwiąż układ równań:

Na bokach AB i AD równoległoboku ABCD wytyczono odpowiednio punkty E i K, tak że odcinek EK jest równoległy do przekątnej BD. Udowodnij, że pola trójkątów ALL i SDO są równe.

Postanowili posadzić grupę turystów w autobusach, tak aby w każdym autobusie znajdowała się taka sama liczba pasażerów. Początkowo do każdego autobusu wsadzono 22 osoby, ale okazało się, że w tym przypadku nie da się umieścić jednego turysty. Kiedy jeden autobus wyjeżdżał pusty, wszyscy turyści równo wsiadali do pozostałych autobusów. Ile autobusów było pierwotnie i ilu turystów było w grupie, jeśli wiadomo, że w każdym autobusie zmieszczą się nie więcej niż 32 osoby?

Zadania do przeprowadzenia powiatowej (miejskiej) olimpiady dla uczniów z matematyki.

Rozwiąż układ równań:

Udowodnij, że cztery odległości od punktu koła do wierzchołka wpisanego w nie kwadratu nie mogą być jednocześnie liczbami wymiernymi.

Możliwe rozwiązania problemów

1. Odpowiedź: x=1, x=0,5

Od permutacji cyfry początkowej do końca znaczenie liczby nie ulegnie zmianie. W tym przypadku, w zależności od stanu problemu, powinni otrzymać liczbę, która jest 5 razy większa niż pierwsza liczba. Dlatego pierwsza cyfra żądanej liczby powinna być równa 1 i tylko 1. (bo jeśli pierwsza cyfra to 2 lub więcej, to wartość się zmieni, 2 * 5 = 10). Po przestawieniu 1 do końca, wynikowa liczba kończy się na 1, dlatego nie jest podzielna przez 5.

Z warunku wynika, że jeśli A i B są przyjaciółmi, to C jest albo ich wspólnym wrogiem, albo wspólnym przyjacielem (w przeciwnym razie nie da się ich pogodzić). Weźmy wszystkich przyjaciół osoby A. Z tego, co zostało powiedziane, wynika, że wszyscy przyjaźnią się ze sobą, a z resztą są wrogo nastawieni. Niech teraz A i jego przyjaciele na zmianę kłócą się z przyjaciółmi i zawierają pokój z wrogami. Potem wszyscy będą przyjaciółmi.

Rzeczywiście, niech A będzie pierwszym, który pokłóci się ze swoimi przyjaciółmi i zawrze pokój ze swoimi wrogami, ale wtedy każdy z jego byłych przyjaciół będzie go tolerował, a dawni wrogowie pozostaną przyjaciółmi. Tak więc wszyscy ludzie okazują się przyjaciółmi A, a co za tym idzie przyjaciółmi między sobą.

Liczba 111 jest podzielna przez 37, więc suma jest również podzielna przez 37.

Warunkowo liczba jest podzielna przez 37, więc suma

Podzielne przez 37.

Zauważ, że wskazana środkowa i dwusieczna nie mogą wychodzić z tego samego wierzchołka, ponieważ w przeciwnym razie kąt w tym wierzchołku byłby większy niż 180 0 . Niech teraz w trójkącie ABC dwusieczna AD i środkowa CE przecinają się w punkcie F. Wtedy AF jest dwusieczną i wysokością w trójkącie ACE, co oznacza, że ten trójkąt jest równoramienny (AC \u003d AE), a ponieważ CE jest mediana, a następnie AB \u003d 2AE, a zatem AB = 2AC.

Możliwe rozwiązania problemów

1. Odpowiedź: 9 strzałów za 8 punktów,

2 strzały za 9 punktów,

1 strzał za 10 punktów.

Pozwalać X strzały oddał zawodnik, wybijając 8 punktów, y rzuty za 9 punktów, z rzuty za 10 punktów. Następnie możesz stworzyć system:

Korzystając z pierwszego równania układu, piszemy:

Z tego systemu wynika, że X+ y+ z=12

Pomnóż drugie równanie przez (-8) i dodaj do pierwszego. Rozumiemy to y+2 z=4 , Gdzie y=4-2 z, y=2(2- z) . Stąd, Na jest liczbą parzystą, tj. y=2t, Gdzie .

Stąd,

3. Odpowiedź: x = -1/2, x = -4

Po sprowadzeniu ułamków do tego samego mianownika otrzymujemy

4. Odpowiedź: 105

Oznacz przez X, y, z odpowiednio pierwszą, drugą i trzecią cyfrę żądanej trzycyfrowej liczby. Wtedy można to zapisać jako . Przekreślenie środkowej cyfry da liczbę dwucyfrową. W zależności od stanu problemu, tj. nieznane numery X, y, z spełnić równanie

7(10 X+ z)=100 X+10 y+ X, który po redukcji podobnych terminów i skrótów przyjmuje postać 3 z=15 X+5 y.

Z tego równania wynika, że z musi być podzielna przez 5 i musi być dodatnia, ponieważ z warunku . Dlatego z = 5 i liczby x, y spełniają równanie 3=3x + y, które na mocy warunku ma jednoznaczne rozwiązanie x = 1, y = 0. Zatem warunek zadania spełnia pojedyncza liczba 105.

Niech F oznacza punkt, w którym przecinają się proste AB i CE. Ponieważ proste DB i CF są równoległe, to . Ponieważ BD jest dwusieczną kąta ABC, wnioskujemy, że . Wynika stąd, że t.j. trójkąt BCF to równoramienny, a BC=BF. Ale wynika to z warunku, że czworokąt BDEF jest równoległobokiem. Dlatego BF = DE, a zatem BC = DE. Podobnie można udowodnić, że AC = DE. Prowadzi to do wymaganej równości.

Możliwe rozwiązania problemów

Stąd (x + y) 2 = 1 , tj. x + y = 1 Lub x + y = -1.

Rozważmy dwa przypadki.

A) x + y = 1. Zastępowanie x = 1 - y

B) x + y = -1. Po podstawieniu x=-1-y

Tak więc tylko następujące cztery pary liczb mogą być rozwiązaniami systemu: (0;1), (2;-1), (-1;0), (1;-2). Podstawiając do równań układu pierwotnego, upewniamy się, że każda z tych czterech par jest rozwiązaniem układu.

Trójkąty CDF i BDF mają wspólną podstawę FD i równe wysokości, ponieważ proste BC i AD są równoległe. Dlatego ich pola są równe. Podobnie pola trójkątów BDF i BDE są równe, ponieważ prosta BD jest równoległa do prostej EF. A pola trójkątów BDE i BCE są równe, ponieważ AB jest równoległa do CD. Oznacza to wymaganą równość pól trójkątów CDF i BCE.

Biorąc pod uwagę dziedzinę definicji funkcji, zbudujemy wykres.

Korzystając z formuły wykonać dalsze przekształcenia

Stosując wzory dodawania i wykonując dalsze przekształcenia, otrzymujemy

5. Odpowiedź: 24 autobusy, 529 turystów.

Oznacz przez k początkowa liczba autobusów. Z warunku problemu wynika, że i że liczba wszystkich turystów jest równa 22 k +1 . Po odjeździe jednego autobusu wszyscy turyści zajmowali miejsca w pozostałych (k-1) autobusy. Dlatego liczba 22 k +1 należy podzielić przez k-1. W ten sposób problem został sprowadzony do wyznaczenia wszystkich liczb całkowitych, dla których dana liczba

Jest liczbą całkowitą i spełnia nierówność (liczba n jest równa liczbie turystów siedzących w każdym autobusie, a zgodnie ze stanem problemu autobus może pomieścić nie więcej niż 32 pasażerów).

Liczba będzie liczbą całkowitą tylko wtedy, gdy liczba jest liczbą całkowitą. To ostatnie jest możliwe tylko z k=2 i o godz k=24 .

Jeśli k=2 , To n=45.

I jeśli k=24 , To n=23.

Z tego iz warunku otrzymujemy tylko to k=24 spełnia wszystkie warunki problemu.

Dlatego początkowo autobusów było 24, a liczba wszystkich turystów wynosi n(k-1)=23*23=529