Twierdzenie Gaussa o indukcji elektrycznej (przemieszczenie elektryczne). IV.Wektor indukcji elektrostatycznej.Przepływ indukcji Twierdzenie Gaussa dla grawitacji Newtona

Gdy ładunków jest wiele, pojawiają się pewne trudności w obliczaniu pól.

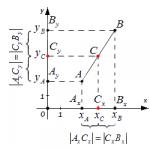
Twierdzenie Gaussa pomaga je przezwyciężyć. istota Twierdzenia Gaussa sprowadza się do następującej postaci: jeśli dowolna liczba ładunków jest mentalnie otoczona przez zamkniętą powierzchnię S, to strumień natężenia pola elektrycznego przez obszar elementarny dS można zapisać jako dФ = Есоsα۰dS, gdzie α jest kątem między normalną do płaszczyzny a wektor intensywności . (rys. 12.7)

Całkowity przepływ przez całą powierzchnię będzie równy sumie przepływów wszystkich ładunków dowolnie rozmieszczonych w jej wnętrzu i proporcjonalny do wartości tego ładunku

(12.9)

Wyznaczmy przepływ wektora napięcia przez sferyczną powierzchnię o promieniu r, w środku której znajduje się ładunek punktowy +q (ryc. 12.8). Linie naprężenia są prostopadłe do powierzchni kuli, α = 0, stąd сosα = 1. Wtedy

Jeśli pole jest utworzone przez system ładunków, to

Twierdzenie Gaussa: przepływ wektora natężenia pola elektrostatycznego w próżni przez dowolną zamkniętą powierzchnię jest równy sumie algebraicznej ładunków zawartych w tej powierzchni, podzielonej przez stałą elektryczną.

(12.10)

Jeśli wewnątrz kuli nie ma żadnych ładunków, to Ф = 0.

Twierdzenie Gaussa sprawia, że ​​stosunkowo łatwo jest obliczyć pola elektryczne dla symetrycznie rozłożonych ładunków.

Wprowadźmy pojęcie gęstości ładunków rozłożonych.

Gęstość liniowa jest oznaczona jako τ i charakteryzuje ładunek q na jednostkę długości ℓ. Ogólnie można to obliczyć za pomocą wzoru

(12.11)

Przy równomiernym rozkładzie ładunków gęstość liniowa jest równa

Gęstość powierzchniowa jest oznaczona σ i charakteryzuje ładunek q na jednostkę powierzchni S. Ogólnie rzecz biorąc, określa się ją wzorem

(12.12)

Przy równomiernym rozkładzie ładunków na powierzchni gęstość powierzchniowa jest równa

Gęstość nasypowa, oznaczona jako ρ, charakteryzuje ładunek q na jednostkę objętości V. Ogólnie określa się go wzorem

(12.13)

Przy równomiernym rozkładzie ładunków jest równy
.

Ponieważ ładunek q jest równomiernie rozłożony na kuli, to

σ = stała Zastosujmy twierdzenie Gaussa. Narysujmy kulę o promieniu przechodzącą przez punkt A. Przepływ wektora natężenia na ryc. 12.9 przez sferyczną powierzchnię promienia wynosi cosα = 1, ponieważ α = 0. Zgodnie z twierdzeniem Gaussa,
.

Lub

(12.14)

Z wyrażenia (12.14) wynika, że ​​natężenie pola na zewnątrz naładowanej kuli jest takie samo, jak natężenie pola ładunku punktowego umieszczonego w środku kuli. Na powierzchni kuli, tj. r 1 \u003d r 0, napięcie
.

Wewnątrz kuli r 1< r 0 (рис.12.9) напряжённость Е = 0, так как сфера радиусом r 2 внутри никаких зарядов не содержит и, по теореме Гаусса, поток вектора сквозь такую сферу равен нулю.

Walec o promieniu r 0 jest równomiernie naładowany gęstością powierzchniową σ (ryc. 12.10). Wyznaczmy natężenie pola w dowolnie wybranym punkcie A. Narysujmy wyimaginowaną cylindryczną powierzchnię o promieniu R i długości ℓ przechodzącą przez punkt A. Ze względu na symetrię przepływ będzie wychodził tylko przez boczne powierzchnie cylindra, ponieważ ładunki na walcu o promieniu r 0 są równomiernie rozłożone na jego powierzchni, tj. linie naprężenia będą promieniowymi liniami prostymi prostopadłymi do powierzchni bocznych obu cylindrów. Ponieważ przepływ przez podstawę cylindrów wynosi zero (cos α = 0), a powierzchnia boczna cylindra jest prostopadła do linii sił (cos α = 1), to

Lub

(12.15)

Wartość E wyrażamy przez σ - gęstość powierzchniową. a-priorytet,

stąd,

Podstaw wartość q we wzorze (12.15)

(12.16)

Z definicji gęstości linii,
, Gdzie
; podstawiamy to wyrażenie do wzoru (12.16):

(12.17)

te. natężenie pola generowane przez nieskończenie długi naładowany cylinder jest proporcjonalne do liniowej gęstości ładunku i odwrotnie proporcjonalne do odległości.

Intensywność pola utworzonego przez nieskończoną, równomiernie naładowaną płaszczyznę

Wyznaczmy natężenie pola wytworzonego przez nieskończoną jednostajnie naładowaną płaszczyznę w punkcie A. Niech gęstość ładunku powierzchniowego płaszczyzny będzie równa σ. Jako powierzchnię zamkniętą wygodnie jest wybrać walec, którego oś jest prostopadła do płaszczyzny, a prawa podstawa zawiera punkt A. Płaszczyzna dzieli walec na pół. Oczywiste jest, że linie sił są prostopadłe do płaszczyzny i równoległe do powierzchni bocznej cylindra, więc cały przepływ przechodzi tylko przez podstawy cylindra. Na obu bazach natężenie pola jest takie samo, ponieważ. punkty A i B są symetryczne względem płaszczyzny. Wtedy przepływ przez podstawy cylindra jest

Zgodnie z twierdzeniem Gaussa,

Ponieważ
, To
, Gdzie

(12.18)

Zatem natężenie pola nieskończenie naładowanej płaszczyzny jest proporcjonalne do gęstości ładunku powierzchniowego i nie zależy od odległości od płaszczyzny. Dlatego pole płaszczyzny jest jednorodne.

Natężenie pola utworzonego przez dwie przeciwnie naładowane, równoległe płaszczyzny

Wynikowe pole utworzone przez dwie płaszczyzny jest określone przez zasadę superpozycji pól:
(rys.12.12). Pole tworzone przez każdą płaszczyznę jest jednorodne, siły tych pól są równe w wartości bezwzględnej, ale przeciwnie skierowane:
. Zgodnie z zasadą superpozycji, całkowite natężenie pola poza płaszczyzną wynosi zero:

Pomiędzy płaszczyznami natężenia pola mają te same kierunki, więc wypadkowa siła jest równa

Zatem pole między dwiema przeciwnie naładowanymi płaszczyznami jest jednorodne, a jego natężenie jest dwukrotnie większe niż natężenie pola wytwarzanego przez jedną płaszczyznę. Po lewej i prawej stronie samolotów nie ma pola. Pole płaszczyzn skończonych ma taką samą postać, zniekształcenie pojawia się tylko w pobliżu ich granic. Korzystając z otrzymanego wzoru, możesz obliczyć pole między okładkami płaskiego kondensatora.

Cel lekcji: Twierdzenie Ostrogradskiego-Gaussa zostało ustalone przez rosyjskiego matematyka i mechanika Michaiła Wasiljewicza Ostrogradskiego w postaci ogólnego twierdzenia matematycznego oraz przez niemieckiego matematyka Carla Friedricha Gaussa. Twierdzenie to może być wykorzystane w badaniu fizyki na poziomie profilu, ponieważ pozwala na bardziej racjonalne obliczenia pól elektrycznych.

Aby wyprowadzić twierdzenie Ostrogradskiego-Gaussa, konieczne jest wprowadzenie tak ważnych pojęć pomocniczych, jak wektor indukcji elektrycznej i strumień tego wektora Ф.

Wiadomo, że pole elektrostatyczne jest często przedstawiane za pomocą linii sił. Załóżmy, że wyznaczamy napięcie w punkcie leżącym na styku dwóch ośrodków: powietrza (=1) i wody (=81). W tym momencie, przy przejściu z powietrza do wody, natężenie pola elektrycznego zgodnie ze wzorem zmniejszy się 81 razy. Jeśli zaniedbamy przewodnictwo wody, to liczba linii sił zmniejszy się o ten sam współczynnik. Podczas rozwiązywania różnych problemów związanych z obliczaniem pól powstają pewne niedogodności z powodu nieciągłości wektora siły na styku mediów i dielektryków. Aby ich uniknąć, wprowadza się nowy wektor, który nazywa się wektorem indukcji elektrycznej:

Wektor indukcji elektrycznej jest równy iloczynowi wektora i stałej elektrycznej oraz przenikalności elektrycznej ośrodka w danym punkcie.

Oczywiście przy przejściu przez granicę dwóch dielektryków liczba linii indukcji elektrycznej nie zmienia się dla pola ładunku punktowego (1).

W układzie SI wektor indukcji elektrycznej mierzony jest w kulombach na metr kwadratowy (C / m2). Wyrażenie (1) pokazuje, że wartość liczbowa wektora nie zależy od właściwości ośrodka. Pole wektorowe jest graficznie przedstawione podobnie jak pole napięcia (na przykład dla ładunku punktowego, patrz ryc. 1). W przypadku pola wektorowego obowiązuje zasada superpozycji:

Strumień indukcji elektrycznej

Wektor indukcji elektrycznej charakteryzuje pole elektryczne w każdym punkcie przestrzeni. Można wprowadzić jeszcze jedną wielkość, w zależności od wartości wektora nie w jednym punkcie, ale we wszystkich punktach powierzchni ograniczonej płaskim konturem zamkniętym.

Aby to zrobić, rozważ płaski, zamknięty przewodnik (obwód) o polu powierzchni S, umieszczony w jednorodnym polu elektrycznym. Normalna do płaszczyzny przewodnika tworzy kąt z kierunkiem wektora indukcji elektrycznej (rys. 2).

Przepływ indukcji elektrycznej przez powierzchnię S nazywamy wartością równą iloczynowi modułu wektora indukcji i powierzchni S oraz cosinusa kąta między wektorem a normalną:

To twierdzenie pozwala znaleźć przepływ wektora indukcji elektrycznej przez zamkniętą powierzchnię, wewnątrz której znajdują się ładunki elektryczne.

Niech pierwszy ładunek punktowy q zostanie umieszczony w środku kuli o dowolnym promieniu r 1 (rys. 3). Następnie ; . Obliczmy całkowity strumień indukcji przechodzący przez całą powierzchnię tej kuli: ; (). Jeśli weźmiemy kulę o promieniu , to również Ф = q. Jeśli narysujemy kulę, która nie zawiera ładunku q, wówczas całkowity przepływ Ф \u003d 0 (ponieważ każda linia wejdzie na powierzchnię, a innym razem ją opuści).

Zatem Ф = q, jeśli ładunek znajduje się wewnątrz zamkniętej powierzchni i Ф = 0, jeśli ładunek znajduje się na zewnątrz zamkniętej powierzchni. Strumień F nie zależy od kształtu powierzchni. Nie zależy również od ułożenia ładunków wewnątrz powierzchni. Oznacza to, że otrzymany wynik jest ważny nie tylko dla jednego ładunku, ale także dla dowolnej liczby dowolnie rozmieszczonych ładunków, jeśli przez q rozumiemy tylko algebraiczną sumę wszystkich ładunków znajdujących się wewnątrz powierzchni.

Twierdzenie Gaussa: przepływ indukcji elektrycznej przez dowolną zamkniętą powierzchnię jest równy algebraicznej sumie wszystkich ładunków wewnątrz powierzchni: .

Ze wzoru widać, że wymiar przepływu prądu elektrycznego jest taki sam jak wymiar ładunku elektrycznego. Dlatego jednostką przepływu indukcji elektrycznej jest zawieszka (C).

Uwaga: jeżeli pole jest niejednorodne, a powierzchnia, przez którą wyznaczany jest przepływ, nie jest płaszczyzną, to powierzchnię tę można podzielić na nieskończenie małe elementy ds i każdy element można uznać za płaski, a pole w jego pobliżu jest jednorodne. Dlatego dla dowolnego pola elektrycznego przepływ wektora indukcji elektrycznej przez element powierzchniowy wynosi: dФ=. W wyniku całkowania całkowity strumień przez zamkniętą powierzchnię S w dowolnym niejednorodnym polu elektrycznym jest równy: , gdzie q jest algebraiczną sumą wszystkich ładunków otoczonych zamkniętą powierzchnią S. Ostatnie równanie wyrażamy w kategoriach natężenia pola elektrycznego (dla próżni): .

Jest to jedno z podstawowych równań Maxwella dla pola elektromagnetycznego, zapisane w postaci całkowej. Pokazuje, że źródłem stałego pola elektrycznego w czasie są nieruchome ładunki elektryczne.

Wyznaczmy teraz, korzystając z twierdzenia Ostrogradskiego-Gaussa, natężenie pola dla pewnej liczby przypadków.

1. Pole elektryczne równomiernie naładowanej kulistej powierzchni.

Kula o promieniu R. Niech ładunek +q będzie równomiernie rozłożony na kulistej powierzchni o promieniu R. Rozkład ładunku na powierzchni charakteryzuje się powierzchniową gęstością ładunku (Rys. 4). Gęstość ładunku powierzchniowego to stosunek ładunku do powierzchni, na której jest on rozłożony. . w SI.

Określmy natężenie pola:

a) poza sferyczną powierzchnią,
b) wewnątrz kulistej powierzchni.

a) Weźmy punkt A, który znajduje się w odległości r>R od środka naładowanej kulistej powierzchni. Narysujmy w myślach sferyczną powierzchnię S o promieniu r, mającą wspólny środek z naładowaną kulistą powierzchnią. Z rozważań o symetrii jest oczywiste, że linie sił są promieniowymi liniami prostymi prostopadłymi do powierzchni S i równomiernie przechodzą przez tę powierzchnię, tj. napięcie we wszystkich punktach tej powierzchni jest stałe co do wielkości. Zastosujmy twierdzenie Ostrogradskiego-Gaussa do tej kulistej powierzchni S o promieniu r. Więc całkowity przepływ przez kulę wynosi N = E? S; N=E. Z drugiej strony . Zrównać: . Stąd: dla r>R.

Zatem: napięcie wytwarzane przez równomiernie naładowaną powierzchnię kuli na zewnątrz jest takie samo, jak gdyby cały ładunek znajdował się w jej środku (ryc. 5).

b) Znajdźmy natężenie pola w punktach leżących wewnątrz naładowanej kulistej powierzchni. Weźmy punkt B oddalony od środka kuli w pewnej odległości . Wtedy , E = 0 dla r

2. Natężenie pola równomiernie naładowanej nieskończonej płaszczyzny

Rozważmy pole elektryczne wytworzone przez nieskończoną płaszczyznę naładowaną ze stałą gęstością we wszystkich punktach płaszczyzny. Ze względu na symetrię możemy przyjąć, że linie naprężeń są prostopadłe do płaszczyzny i skierowane od niej w obu kierunkach (rys. 6).

Wybieramy punkt A leżący na prawo od płaszczyzny i obliczamy w tym punkcie korzystając z twierdzenia Ostrogradskiego-Gaussa. Jako powierzchnię zamkniętą wybieramy powierzchnię cylindryczną tak, aby powierzchnia boczna walca była równoległa do linii sił, a jego podstawy i były równoległe do płaszczyzny, a podstawa przechodziła przez punkt A (ryc. 7). Obliczmy strumień naprężenia przez rozważaną powierzchnię cylindryczną. Przepływ przez powierzchnię boczną wynosi 0, ponieważ linie napięcia są równoległe do powierzchni bocznej. Wtedy całkowity przepływ jest sumą przepływów i przechodzących przez podstawy cylindra i . Oba te przepływy są dodatnie =+; =; =; ==; N=2.

- przekrój płaszczyzny leżący wewnątrz wybranej powierzchni cylindrycznej. Ładunek wewnątrz tej powierzchni wynosi q.

Następnie ; - może być traktowany jako ładunek punktowy) z punktem A. Aby znaleźć pole całkowite, należy dodać geometrycznie wszystkie pola utworzone przez każdy element: ; .

Sformułowanie ogólne: Przepływ wektora natężenia pola elektrycznego przez dowolnie wybraną powierzchnię zamkniętą jest proporcjonalny do ładunku elektrycznego zawartego w tej powierzchni.

W systemie GSSE:

W układzie SI:

jest przepływem wektora natężenia pola elektrycznego przez zamkniętą powierzchnię.

to całkowity ładunek zawarty w objętości, która ogranicza powierzchnię.

jest stałą elektryczną.

To wyrażenie jest twierdzeniem Gaussa w postaci całkowej.

W postaci różniczkowej twierdzenie Gaussa odpowiada jednemu z równań Maxwella i wyraża się następująco

w układzie SI:

,

w systemie GSSE:

Tutaj jest objętościową gęstością ładunku (w przypadku obecności ośrodka, całkowitą gęstością ładunków swobodnych i związanych), a jest operatorem nabla.

W przypadku twierdzenia Gaussa obowiązuje zasada superpozycji, to znaczy strumień wektora naprężenia przez powierzchnię nie zależy od rozkładu ładunku wewnątrz powierzchni.

Fizyczną podstawą twierdzenia Gaussa jest prawo Coulomba lub inaczej, twierdzenie Gaussa jest integralnym sformułowaniem prawa Coulomba.

Twierdzenie Gaussa o indukcji elektrycznej (przemieszczenie elektryczne).

Dla pola w substancji elektrostatyczne twierdzenie Gaussa można zapisać w inny sposób - poprzez przepływ wektora przemieszczenia elektrycznego (indukcja elektryczna). W tym przypadku sformułowanie twierdzenia jest następujące: przepływ wektora przemieszczenia elektrycznego przez zamkniętą powierzchnię jest proporcjonalny do swobodnego ładunku elektrycznego wewnątrz tej powierzchni:

Jeśli weźmiemy pod uwagę twierdzenie o natężeniu pola w substancji, to jako ładunek Q należy przyjąć sumę ładunku swobodnego znajdującego się wewnątrz powierzchni i ładunku polaryzacyjnego (indukowanego, związanego) dielektryka:

,

Gdzie ,
jest wektorem polaryzacji dielektryka.

Twierdzenie Gaussa o indukcji magnetycznej

Strumień wektora indukcji magnetycznej przez dowolną zamkniętą powierzchnię wynosi zero:

.

Jest to równoważne z faktem, że w naturze nie ma „ładunków magnetycznych” (monopoli), które tworzyłyby pole magnetyczne, tak jak ładunki elektryczne tworzą pole elektryczne. Innymi słowy, twierdzenie Gaussa dotyczące indukcji magnetycznej pokazuje, że pole magnetyczne jest wirowe.

Zastosowanie twierdzenia Gaussa

Następujące wielkości są używane do obliczania pól elektromagnetycznych:

Gęstość ładunku masowego (patrz wyżej).

Gęstość ładunku powierzchniowego

gdzie dS jest nieskończenie małym obszarem powierzchni.

Liniowa gęstość ładunku

gdzie dl jest długością nieskończenie małego segmentu.

Rozważmy pole utworzone przez nieskończoną jednorodną naładowaną płaszczyznę. Niech gęstość ładunku powierzchniowego płaszczyzny będzie taka sama i równa σ. Wyobraź sobie w myślach cylinder z generatorami prostopadłymi do płaszczyzny i podstawą ΔS umieszczoną symetrycznie względem płaszczyzny. Ze względu na symetrię. Strumień wektora natężenia jest równy . Stosując twierdzenie Gaussa, otrzymujemy:

,

z którego

w systemie GSSE

Należy zauważyć, że pomimo swojej uniwersalności i ogólności, twierdzenie Gaussa w postaci całkowej ma stosunkowo ograniczone zastosowanie ze względu na niedogodności związane z obliczaniem całki. Jednak w przypadku problemu symetrycznego jego rozwiązanie staje się znacznie prostsze niż zastosowanie zasady superpozycji.

Najtrudniejsze jest badanie zjawisk elektrycznych w niejednorodnym ośrodku elektrycznym. W takim ośrodku ε ma różne wartości, zmieniając się gwałtownie na granicy dielektryków. Załóżmy, że wyznaczamy natężenie pola na styku dwóch ośrodków: ε 1 = 1 (próżnia lub powietrze) i ε 2 = 3 (ciecz - olej). Na granicy faz, podczas przejścia od próżni do dielektryka, natężenie pola zmniejsza się trzykrotnie, a strumień wektora siły zmniejsza się o tę samą wartość (ryc. 12.25, a). Nagła zmiana wektora natężenia pola elektrostatycznego na styku dwóch ośrodków stwarza pewne trudności w obliczaniu pól. Jeśli chodzi o twierdzenie Gaussa, w tych warunkach generalnie traci ono swoje znaczenie.

Ponieważ polaryzowalność i intensywność różnych dielektryków są różne, liczba linii pola w każdym dielektryku również będzie inna. Tę trudność można wyeliminować, wprowadzając nową charakterystykę fizyczną pola, indukcję elektryczną D (lub wektor przemieszczenie elektryczne ).

Zgodnie z formułą

ε 1 mi 1 \u003d ε 2 mi 2 \u003d mi 0 \u003d stała

Mnożąc wszystkie części tych równości przez stałą elektryczną ε 0 otrzymujemy

ε 0 ε 1 mi 1 = ε 0 ε 2 mi 2 = ε 0 mi 0 = stała

Wprowadźmy oznaczenie ε 0 εЕ=D wtedy przedostatnia relacja przyjmie postać

re 1 = re 2 = re 0 = stała

Nazywa się wektor D, równy iloczynowi natężenia pola elektrycznego w dielektryku i jego bezwzględnej przenikalności elektrycznejwektor przemieszczenia elektrycznego

(12.45)

Jednostką przemieszczenia elektrycznego jest wisiorek za metr kwadratowy(C/m2).

Przemieszczenie elektryczne jest wielkością wektorową, można je również wyrazić jako

re = εε 0 mi = (1+χ)ε 0 mi = ε 0 mi + χε 0 mi = ε 0 mi+p

(12.46)

W przeciwieństwie do napięcia E, przemieszczenie elektryczne D jest stałe we wszystkich dielektrykach (ryc. 12.25, b). Dlatego wygodnie jest scharakteryzować pole elektryczne w niejednorodnym ośrodku dielektrycznym nie za pomocą natężenia E, ale wektora przemieszczenia D. Wektor D opisuje pole elektrostatyczne wytwarzane przez ładunki swobodne (tj. w próżni), ale z ich rozkładem w przestrzeni, czyli w obecności dielektryka, gdyż powstające w dielektryku ładunki związane mogą powodować redystrybucję ładunków swobodnych tworząc pole .

Pole wektorowe jest graficznie reprezentowany przez linie przemieszczenia elektrycznego w taki sam sposób jak pole reprezentowane przez linie sił.

Linia przemieszczenia elektrycznego są liniami, których styczne w każdym punkcie pokrywają się z kierunkiem wektora przemieszczenia elektrycznego.

Linie wektora E mogą zaczynać się i kończyć na dowolnych ładunkach – swobodnych i związanych, natomiast linie wektoraD- tylko za darmo. Linie wektoroweDw przeciwieństwie do linii napięcia są ciągłe.

Ponieważ wektor przemieszczenia elektrycznego nie doświadcza nieciągłości na granicy między dwoma ośrodkami, to wszystkie linie indukcji pochodzące od ładunków otoczonych jakąś zamkniętą powierzchnią będą przez niego przenikać. Dlatego dla wektora przemieszczenia elektrycznego twierdzenie Gaussa całkowicie zachowuje swoje znaczenie dla niejednorodnego ośrodka dielektrycznego.

Twierdzenie Gaussa o polu elektrostatycznym w dielektryku : przepływ wektora przemieszczenia elektrycznego przez dowolną zamkniętą powierzchnię jest równy sumie algebraicznej ładunków zawartych w tej powierzchni.

(12.47)

Przepływ wektora natężenia pola elektrycznego. Niech mały plac zabaw DS(ryc. 1.2) przecinają linie sił pola elektrycznego, których kierunek jest zgodny z normalną N rogu tej witryny A. Zakładając, że wektor napięcia mi nie zmienia się w witrynie DS, definiować przepływ wektora napięcia przez witrynę DS Jak

DFmi =mi DS sałata A.(1.3)

Ponieważ gęstość linii pola jest równa liczbowej wartości napięcia mi, a następnie liczbę linii sił przecinających ten obszarDS, będzie liczbowo równa wartości strumieniaDFmiprzez powierzchnięDS. Prawą stronę wyrażenia (1.3) reprezentujemy jako iloczyn skalarny wektorów mi IDS= NDS, Gdzie Njest jednostkowym wektorem normalnym do powierzchniDS. Dla obszaru elementarnego d S wyrażenie (1.3) przyjmuje postać

DFmi = mi D S

w całej witrynie S strumień wektora natężenia jest obliczany jako całka po powierzchni

Przepływ wektora indukcji elektrycznej. Przepływ wektora indukcji elektrycznej wyznacza się podobnie jak przepływ wektora natężenia pola elektrycznego

DFD = D D S

Istnieje pewna niejasność w definicjach przepływów, ponieważ dla każdej powierzchni można określić dwa normalne w przeciwnym kierunku. W przypadku powierzchni zamkniętej normalną zewnętrzną uważa się za dodatnią.

Twierdzenie Gaussa. Rozważać punkt dodatniładunek elektryczny Q, znajdujące się wewnątrz dowolnej zamkniętej powierzchni S(Rys. 1.3). Przepływ wektora indukcji przez element powierzchniowy d S równa się
(1.4)

Składnik D S D = D S sałata Aelement powierzchniowy d S w kierunku wektora indukcyjnegoDtraktowany jako element kulistej powierzchni o promieniu R, w środku którego znajduje się ładunekQ.

Biorąc pod uwagę, że D S D/ R 2 równe elementarna cielesność róg Dw, pod którym od punktu, w którym opłataQwidoczny element powierzchniowy d S, przekształcamy wyrażenie (1.4) do postaci D FD = Q D w / 4 P, skąd po całkowaniu po całej przestrzeni otaczającej ładunek, czyli w obrębie kąta bryłowego od 0 do 4P, dostajemy

FD = Q.

Przepływ wektora indukcji elektrycznej przez zamkniętą powierzchnię o dowolnym kształcie jest równy ładunkowi zawartemu w tej powierzchni.

Jeśli dowolna zamknięta powierzchnia S nie obejmuje opłaty punktowej Q(ryc. 1.4), a następnie po zbudowaniu stożkowej powierzchni z wierzchołkiem w punkcie, w którym znajduje się ładunek, dzielimy powierzchnię S na dwie części: S 1 i S 2. Przepływ wektora D przez powierzchnię S znajdujemy jako algebraiczną sumę przepływów przez powierzchnie S 1 i S 2:

.

Obie powierzchnie od punktu, w którym znajduje się ładunek Q widoczne pod jednym stałym kątem w. Przepływy są więc równe

Ponieważ przy obliczaniu przepływu przez zamkniętą powierzchnię używamy zewnętrzna normalna na powierzchnię, łatwo zauważyć, że strumień Ф 1D < 0, тогда как поток Ф2D> 0. Całkowity przepływ Ф D= 0. Oznacza to, że przepływ wektora indukcji elektrycznej przez zamkniętą powierzchnię o dowolnym kształcie nie zależy od ładunków znajdujących się poza tą powierzchnią.

Jeśli pole elektryczne jest wytwarzane przez system ładunków punktowych Q 1 , Q 2 ,¼ , q n, która jest pokryta zamkniętą powierzchnią S, to zgodnie z zasadą superpozycji strumień wektora indukcji przez tę powierzchnię definiuje się jako sumę strumieni wytwarzanych przez każdy z ładunków. Przepływ wektora indukcji elektrycznej przez zamkniętą powierzchnię o dowolnym kształcie jest równy sumie algebraicznej ładunków znajdujących się na tej powierzchni:

Należy zauważyć, że opłaty qi niekoniecznie muszą być punktowe, warunkiem koniecznym jest, aby naładowany obszar był całkowicie pokryty powierzchnią. Jeśli w przestrzeni ograniczonej zamkniętą powierzchnią S, ładunek elektryczny rozkłada się w sposób ciągły, to należy przyjąć, że każda elementarna objętość d V ma opłatę. W tym przypadku po prawej stronie wyrażenia (1.5) algebraiczne sumowanie ładunków zastąpiono całkowaniem po objętości zamkniętej w powierzchni zamkniętej S:

(1.6)

Wyrażenie (1.6) jest najbardziej ogólnym sformułowaniem Twierdzenia Gaussa: strumień wektora indukcji elektrycznej przez zamkniętą powierzchnię o dowolnym kształcie jest równy całkowitemu ładunkowi w objętości objętej tą powierzchnią i nie zależy od ładunków znajdujących się poza rozważaną powierzchnią. Twierdzenie Gaussa można również zapisać dla przepływu wektora natężenia pola elektrycznego:

.

Ważna właściwość pola elektrycznego wynika z twierdzenia Gaussa: linie siły zaczynają się lub kończą tylko na ładunkach elektrycznych lub idą w nieskończoność. Jeszcze raz podkreślamy, że pomimo tego, że natężenie pola elektrycznego mi i indukcji elektrycznej D zależą od położenia wszystkich ładunków w przestrzeni, strumienie tych wektorów przez dowolną zamkniętą powierzchnię S tylko zdeterminowany te ładunki, które znajdują się wewnątrz powierzchni S.

Różniczkowa postać twierdzenia Gaussa. Zauważ to integralna forma twierdzenie Gaussa charakteryzuje zależność między źródłami pola elektrycznego (ładunki) a charakterystyką pola elektrycznego (natężenie lub indukcja) w objętości V arbitralna, ale wystarczająca do ukształtowania integralnych relacji, wartość. Dzieląc objętość V dla małych objętości wi, otrzymujemy wyrażenie

ważne zarówno ogólnie, jak i dla każdej kadencji. Wynikowe wyrażenie przekształcamy w następujący sposób:

(1.7)

i rozważmy granicę, do której dąży wyrażenie po prawej stronie równości, ujęte w nawiasy klamrowe, przy nieograniczonym podziale objętości V. W matematyce ta granica nazywa się rozbieżność wektor (w tym przypadku wektor indukcji elektrycznej D):

Rozbieżność wektorów D we współrzędnych kartezjańskich:

Zatem wyrażenie (1.7) przekształca się do postaci:

.

Biorąc pod uwagę, że przy nieograniczonym dzieleniu suma po lewej stronie ostatniego wyrażenia przechodzi do całki objętościowej, otrzymujemy

Wynikowa relacja musi być zachowana dla dowolnej dowolnie wybranej objętości V. Jest to możliwe tylko wtedy, gdy wartości całek w każdym punkcie przestrzeni są takie same. Dlatego rozbieżność wektora D jest powiązany z gęstością ładunku w tym samym punkcie przez równość

lub dla wektora natężenia pola elektrostatycznego

Te równości wyrażają twierdzenie Gaussa w postać różniczkowa.

Należy zauważyć, że w procesie przechodzenia do postaci różniczkowej twierdzenia Gaussa uzyskuje się zależność, która ma charakter ogólny:

.

Wyrażenie nazywa się wzorem Gaussa-Ostrogradskiego i łączy całkę objętościową z rozbieżności wektora z przepływem tego wektora przez zamkniętą powierzchnię, która ogranicza objętość.

pytania

1) Jakie jest fizyczne znaczenie twierdzenia Gaussa dla pola elektrostatycznego w próżni

2) W środku sześcianu znajduje się ładunek punktowyQ. Jaki jest przepływ wektora mi:

a) przez całą powierzchnię sześcianu; b) przez jedną ze ścian sześcianu.

Czy odpowiedzi zmienią się, jeśli:

a) ładunek nie znajduje się w środku sześcianu, ale w jego wnętrzu ; b) ładunek znajduje się poza sześcianem.

3) Co to jest liniowa, powierzchniowa, objętościowa gęstość ładunku.

4) Wskaż zależność między objętością a gęstością ładunku powierzchniowego.

5) Czy pole na zewnątrz przeciwnie i równomiernie naładowanych równoległych nieskończonych płaszczyzn może być różne od zera

6) Dipol elektryczny jest umieszczony wewnątrz zamkniętej powierzchni. Jaki jest przepływ przez tę powierzchnię