Lemat o punkcie granicznym ciągu. Punkty graniczne ciągu liczb porządkowych Dowód kryterium Weierstrassa i kryterium Cauchy'ego

Twierdzenie Bolzano-Weierstrassa

Twierdzenie Bolzano-Weierstrassa, Lub Lemat Bolzano-Weierstrassa o punkcie granicznym- propozycja analizy, której jedno ze sformułowań mówi: z dowolnego ograniczonego ciągu punktów w przestrzeni można wyróżnić podciąg zbieżny. Twierdzenie Bolzano-Weierstrassa, zwłaszcza przypadek ciągu liczbowego ( N= 1 ), jest uwzględniony w każdym przebiegu analizy. Jest używany w dowodzie wielu propozycji analizy, na przykład twierdzenia o osiągnięciu funkcji ciągłej na odcinku przez jego najlepsze górne i dolne granice. Twierdzenie nosi nazwiska czeskiego matematyka Bolzano i niemieckiego matematyka Weierstrassa, którzy niezależnie je sformułowali i udowodnili.

Sformułowanie

Znanych jest kilka sformułowań twierdzenia Bolzano-Weierstrassa.

Pierwsze sformułowanie

Zaproponujmy ciąg punktów w przestrzeni:

i niech ten ciąg będzie ograniczony, tj.

Gdzie C> 0 - jakaś liczba.

Następnie z tej sekwencji możemy wybrać podsekwencję

które zbiegają się do pewnego punktu w przestrzeni.

Twierdzenie Bolzano-Weierstrassa w tym sformułowaniu jest czasami nazywane zasada zwartości ciągu ograniczonego.

Rozszerzona wersja pierwszego brzmienia

Często twierdzenie Bolzano-Weierstrassa jest uzupełniane następującym twierdzeniem.

Jeżeli ciąg punktów w przestrzeni jest nieograniczony, to można wybrać z niego ciąg, który ma granicę.

Z okazji N= 1 to sformułowanie można udoskonalić: z dowolnego nieograniczonego ciągu liczbowego można wybrać podsekwencję, która ma granicę nieskończoności określonego znaku ( lub ).

Zatem każda sekwencja liczb zawiera podsekwencję, która ma granicę w rozszerzonym zbiorze liczb rzeczywistych.

Drugie sformułowanie

Poniższe twierdzenie jest alternatywnym sformułowaniem twierdzenia Bolzano-Weierstrassa.

Każdy ograniczony nieskończony podzbiór mi przestrzeń ma co najmniej jeden punkt graniczny w .

Bardziej szczegółowo oznacza to, że istnieje punkt, którego każde otoczenie zawiera nieskończoną liczbę punktów zbioru mi .

Dowód równoważności dwóch sformułowań twierdzenia Bolzano-Weierstrassa

Pozwalać mi jest ograniczonym nieskończonym podzbiorem przestrzeni . Weźmy się w garść mi kolejność różnych punktów

Ponieważ ciąg ten jest ograniczony, na mocy pierwszego sformułowania twierdzenia Bolzano – Weierstrassa można z niego wyodrębnić podciąg

zbiegające się do pewnego punktu. Następnie każde otoczenie punktu X 0 zawiera nieskończoną liczbę punktów w zbiorze mi .

Wiele wartości mi dana sekwencja jest ograniczona, ale może być nieskończona lub skończona. Jeśli mi oczywiście wtedy jedna z wartości powtarza się w sekwencji nieskończoną ilość razy. Wtedy wyrazy te tworzą stacjonarny podciąg zbiegający się do punktu A .

Jeśli zestaw mi nieskończenie więc, na mocy drugiego sformułowania twierdzenia Bolzano-Weierstrassa, istnieje punkt, w dowolnym sąsiedztwie którego istnieje nieskończenie wiele różnych elementów ciągu.

Wybieramy kolejno dla zwrotnica obserwując warunek rosnących liczb:

Dowód

Twierdzenie Bolzano-Weierstrassa wywodzi się z własności zupełności zbioru liczb rzeczywistych. Najbardziej znany wariant dowodu wykorzystuje właściwość kompletności w postaci zasady zagnieżdżonych segmentów.

Sprawa jednowymiarowa

Udowodnijmy, że z dowolnego ograniczonego ciągu liczbowego można wybrać podciąg zbieżny. Nazywa się następujący dowód Metoda Bolzano, Lub metoda bisekcji.

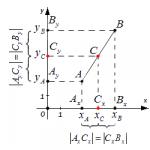
Niech dany będzie ograniczony ciąg liczbowy

Z ograniczoności ciągu wynika, że ​​wszystkie jego elementy leżą na pewnym odcinku prostej rzeczywistej, którą oznaczamy przez [ A 0 ,B 0 ] .

Podziel segment [ A 0 ,B 0 ] na pół na dwa równe segmenty. Co najmniej jeden z wynikowych segmentów zawiera nieskończoną liczbę terminów w sekwencji. Oznaczmy to [ A 1 ,B 1 ] .

W kolejnym kroku powtarzamy procedurę z segmentem [ A 1 ,B 1 ] : dzielimy go na dwa równe odcinki i wybieramy z nich ten, który zawiera nieskończoną liczbę wyrazów ciągu. Oznaczmy to [ A 2 ,B 2 ] .

Kontynuując proces, otrzymujemy sekwencję zagnieżdżonych segmentów

w którym każdy kolejny jest połową poprzedniego i zawiera nieskończoną liczbę elementów ciągu ( X k } .

Długości odcinków dążą do zera:

Na mocy zasady Cauchy'ego-Cantora dotyczącej zagnieżdżonych segmentów istnieje jeden punkt ξ, który należy do wszystkich segmentów:

Według konstrukcji na każdym segmencie [A M ,B M ] ciąg ma nieskończoną liczbę wyrazów. Wybierajmy po kolei

obserwując warunek rosnących liczb:

Następnie podciąg zbiega się do punktu ξ. Wynika to z faktu, że odległość od do ξ nie przekracza długości zawierającego je odcinka [A M ,B M ] , Gdzie

Rozszerzenie na przypadek przestrzeni o dowolnym wymiarze

Twierdzenie Bolzano-Weierstrassa można łatwo uogólnić na przypadek przestrzeni o dowolnym wymiarze.

Niech dany będzie ciąg punktów w przestrzeni:

(dolny indeks to numer elementu sekwencji, górny to numer współrzędnej). Jeżeli ciąg punktów w przestrzeni jest ograniczony, to każdy z numerycznych ciągów współrzędnych:

również ograniczone ( - numer współrzędnej).

Ze względu na jednowymiarową wersję twierdzenia Bolzano-Weirstrassa z ciągu ( X k) możemy wybrać podciąg punktów, których pierwsze współrzędne tworzą ciąg zbieżny. Z wynikowego podciągu ponownie wybieramy podciąg zbieżny w drugiej współrzędnej. W tym przypadku zbieżność w pierwszej współrzędnej jest zachowana, ponieważ każdy podciąg ciągu zbieżnego również jest zbieżny. I tak dalej.

Po N kroków otrzymujemy pewną sekwencję

który jest podciągiem , i zbiega się w każdej ze współrzędnych. Wynika z tego, że ten podciąg jest zbieżny.

Fabuła

Twierdzenie Bolzano-Weierstrassa (dla przypadku N= 1 ) został po raz pierwszy udowodniony przez czeskiego matematyka Bolzano w 1817 roku. W pracy Bolzano pojawił się jako lemat w dowodzie twierdzenia o wartościach pośrednich funkcji ciągłej, znanego obecnie jako twierdzenie Bolzano-Cauchy'ego. Jednak te i inne wyniki, udowodnione przez Bolzano na długo przed Cauchym i Weierstrassem, przeszły niezauważone.

Zaledwie pół wieku później Weierstrass, niezależnie od Bolzano, ponownie odkrył i udowodnił to twierdzenie. Pierwotnie nazywany twierdzeniem Weierstrassa, zanim praca Bolzano stała się znana i zyskała uznanie.

Dziś twierdzenie to nosi imiona Bolzano i Weierstrassa. Twierdzenie to jest często nazywane Lemat Bolzano-Weierstrassa, i czasami lemat punktu granicznego.

Twierdzenie Bolzano-Weierstrassa i pojęcie zwartości

Twierdzenie Bolzano-Weierstrassa ustanawia następującą interesującą właściwość zbioru ograniczonego: dowolny ciąg punktów M zawiera zbieżny podciąg.

Przy dowodzeniu różnych twierdzeń w analizie często stosuje się następującą sztuczkę: określa się ciąg punktów, który ma jakąś pożądaną właściwość, a następnie wybiera się z niego podciąg, który również ją posiada, ale już jest zbieżny. Na przykład w ten sposób dowodzi się twierdzenia Weierstrassa, że ​​funkcja ciągła na przedziale jest ograniczona i przyjmuje swoje największe i najmniejsze wartości.

Skuteczność takiej techniki w ogóle, a także chęć rozszerzenia twierdzenia Weierstrassa na dowolne przestrzenie metryczne, skłoniły w 1906 roku francuskiego matematyka Maurice'a Frécheta do wprowadzenia pojęcia ścisłość. Własnością zbiorów ograniczonych w , ustaloną przez twierdzenie Bolzano-Weierstrassa, jest, mówiąc obrazowo, że punkty zbioru leżą dość „ściśle” lub „zwarto”: po wykonaniu nieskończonej liczby kroków wzdłuż tego zbioru z pewnością zbliży się tak blisko, jak nam się podoba - do punktu w przestrzeni.

Fréchet wprowadza następującą definicję: zbiór M zwany kompaktowy, Lub kompaktowy, jeśli dowolny ciąg jego punktów zawiera podciąg zbiegający się do jakiegoś punktu tego zbioru. Zakłada się, że na planie M metryka jest zdefiniowana, to znaczy jest

Przypomnijmy sobie, że sąsiedztwo punktu nazwaliśmy przedziałem zawierającym ten punkt; - sąsiedztwo punktu x - interwał

Definicja 4. Punkt nazywamy punktem granicznym zbioru, jeżeli w dowolnym sąsiedztwie tego punktu znajduje się nieskończony podzbiór zbioru X.

Warunek ten jest oczywiście równoważny z faktem, że w dowolnym sąsiedztwie punktu istnieje co najmniej jeden punkt zbioru X, który nie pokrywa się z. (Sprawdź!)

Podajmy kilka przykładów.

Jeśli wtedy tylko punkt jest ograniczeniem dla X.

Dla przedziału każdy punkt odcinka jest graniczny iw tym przypadku nie ma innych punktów granicznych.

Dla zbioru liczb wymiernych każdy punkt E jest graniczny, ponieważ jak wiemy w każdym przedziale liczb rzeczywistych znajdują się liczby wymierne.

Lemat (Bolzano-Weierstrassa). Każdy nieskończony zbiór liczb ograniczonych ma co najmniej jeden punkt graniczny.

Niech X będzie danym podzbiorem E. Z definicji ograniczoności zbioru X wynika, że ​​X jest zawarty w pewnym segmencie. Pokażmy, że przynajmniej jeden z punktów odcinka I jest punktem granicznym dla X.

Gdyby tak nie było, to każdy punkt miałby otoczenie, w którym albo w ogóle nie ma punktów zbioru X, albo jest ich tam skończona liczba. Zbiór takich sąsiadów skonstruowanych dla każdego punktu tworzy pokrycie odcinka I przedziałami, z których zgodnie z lematem o skończonym pokryciu można wyodrębnić skończony układ przedziałów obejmujący odcinek I. Ponieważ jednak układ ten obejmuje cały zbiór X. Jednak w każdym przedziale tylko skończona liczba punktów zbioru X, stąd też ich suma ma również skończoną liczbę punktów X, tj. X jest zbiorem skończonym. Otrzymana sprzeczność kończy dowód.

Definicja w.7. Punkt x ∈ R na prostej rzeczywistej nazywamy punktem granicznym ciągu (xn), jeśli dla dowolnego sąsiedztwa U(x) i dowolnej liczby naturalnej N można znaleźć element xn należący do tego sąsiedztwa o liczbie większej niż λ, tj. x 6 R - punkt graniczny, jeśli. Innymi słowy, punkt x będzie punktem granicznym dla (xn), jeśli elementy tego ciągu o dowolnie dużych liczbach mieszczą się w którymkolwiek z jego sąsiedztw, chociaż być może nie wszystkie elementy o liczbach n > N. Dlatego następujące twierdzenie jest dość oczywiste. Oświadczenie b.b. Jeśli lim(xn) = 6 6 R, to b jest jedynym punktem granicznym ciągu (xn). Rzeczywiście, na mocy definicji 6.3 granicy ciągu, wszystkie jego elementy wychodzące z pewnej liczby mieszczą się w dowolnie małym sąsiedztwie punktu 6, a zatem elementy o dowolnie dużych liczbach nie mogą należeć do żadnego innego punktu. W konsekwencji warunek Definicji 6.7 jest spełniony tylko dla unikalnego punktu 6. Jednak nie każdy punkt graniczny (nazywany czasem dobrze skondensowanym punktem) ciągu jest jego granicą. Zatem ciąg (b.b) nie ma granicy (patrz przykład 6.5), ale ma dwa punkty graniczne x = 1 i x = - 1. Ciąg ((-1)n) ma dwa punkty nieskończone + oo i - z rozszerzona oś liczbowa, której suma jest oznaczona jednym symbolem oo. Dlatego możemy przyjąć, że nieskończone punkty graniczne pokrywają się, a nieskończony punkt oo, zgodnie z (6.29), jest granicą tego ciągu. Punkty graniczne ciągu liczb porządkowych Dowód kryterium Weierstrassa i kryterium Cauchy'ego. Niech będzie dany ciąg (sn) i niech liczby k tworzą rosnący ciąg dodatnich liczb całkowitych. Wtedy ciąg (ynb, gdzie yn = xkn) nazywamy podciągiem ciągu oryginalnego. Oczywiście, jeśli (in) ma jako granicę liczbę 6, to każdy z jego podciągów ma tę samą granicę, ponieważ wychodząc od pewnej liczby, wszystkie elementy zarówno ciągu pierwotnego, jak i któregokolwiek z jego podciągów mieszczą się w dowolnie wybranym sąsiedztwie punktu 6. Jednocześnie dowolny punkt graniczny podciągu jest jednocześnie punktem granicznym ciągu. Niech b będzie punktem granicznym ciągu ciąg (xn), to zgodnie z definicją 6. 7 punkt graniczny, dla każdego n istnieje element należący do otoczenia U (6, 1/n) punktu b o promieniu 1/n. Podciąg złożony z punktów ijtj, ...1 ..., gdzie zjfcn€U(6, 1/n) Vn 6 N, ma jako granicę punkt 6. Rzeczywiście, dla dowolnego e > 0 można wybrać N takie. Wówczas wszystkie elementy podciągu, począwszy od liczby km, mieszczą się w ^-sąsiedztwie U(6, ε) punktu 6, co odpowiada warunkowi z Definicji 6.3 granicy ciągu. Twierdzenie odwrotne jest również prawdziwe. Punkty graniczne ciągu liczb porządkowych Dowód kryterium Weierstrassa i kryterium Cauchy'ego. Twierdzenie 8.10. Jeśli jakiś ciąg ma podciąg z granicą 6, to b jest punktem granicznym tego ciągu. Z definicji 6.3 granicy ciągu wynika, że ​​począwszy od pewnej liczby wszystkie elementy podciągu z granicą b mieszczą się w sąsiedztwie U(b, ​​e) o dowolnym promieniu e. Ponieważ elementy podciągu są jednocześnie elementy ciągu dowolnie dużymi liczbami, a to na mocy definicji 6.7 oznacza, że ​​b jest punktem granicznym ciągu (n). Uwaga 0.2. Twierdzenia 6.9 i 6.10 są również ważne w przypadku, gdy punkt graniczny jest nieskończony, jeśli w dowodzeniu martwego sąsiedztwa U(6, 1 /n) rozważymy sąsiedztwo (lub sąsiedztwa) Warunek, pod którym można odróżnić podciąg zbieżny od ciąg jest tworzony przez następujące twierdzenie: Twierdzenie 6.11 (Bolzano - Weierstrass.) Każdy ciąg ograniczony zawiera podsekwencję zbieżną do skończonej granicy. Niech wszystkie elementy ciągu (an) będą między liczbami a i 6, tj. xn € [ a, b] Vn € N. Podziel odcinek [a , b] na pół. Wtedy co najmniej jedna z jego połówek będzie zawierała nieskończoną liczbę elementów ciągu, ponieważ w przeciwnym razie cały odcinek [a, b] zawierałby ich skończona liczba, co jest niemożliwe Niech ] będzie połową odcinka [a , 6], który zawiera nieskończony zbiór elementów ciągu (xp) (lub jeśli obie połowy są takie, to dowolna z nich ). Kontynuując ten proces konstruujemy układ zagnieżdżonych segmentów, gdzie bn - an = (6 - a)/2n. Zgodnie z zasadą zagnieżdżonych segmentów istnieje punkt x, który należy do wszystkich tych segmentów. Ten punkt będzie punktem granicznym dla ciągu (xn). Rzeczywiście, dla dowolnego e-sąsiedztwa Wx, e) = (x x + e) ​​​​punktu x istnieje odcinek C U(x, e) (to wystarczy wybrać n z nierówności (, zawierającej nieskończoną liczbę elementów ciągu (sn). Zgodnie z definicją 6,7 x jest punktem granicznym tego ciągu. Wtedy na mocy Twierdzenia 6.9 istnieje podciąg zbieżny do punktu x. Metoda rozumowania zastosowana w dowodzie tego twierdzenia (czasami nazywana lematem Bolzano-Weierstrassa) i związana z kolejnymi bisekcjami rozpatrywanych odcinków jest znana jako metoda Bolzano. To twierdzenie znacznie upraszcza dowód wielu złożonych twierdzeń. Pozwala nam udowodnić szereg kluczowych twierdzeń w inny (czasami prostszy) sposób. Dodatek 6.2. Dowód testu Weierstrassa i kryterium Cauchy'ego Najpierw udowodnimy Twierdzenie 6.1 (test Weierstrassa dla zbieżności ograniczonego ciągu monotonicznego). Załóżmy, że ciąg (n) nie jest malejący. Wtedy zbiór jego wartości jest ograniczony z góry i zgodnie z Twierdzeniem 2.1 ma największe supremum, które oznaczamy przez sup(xn) be R. Ze względu na własności największego supremum (patrz 2.7) Zgodnie z Definicją 6.1 dla ciągu niemalejącego mamy or Wtedy > Ny i uwzględniając (6.34) otrzymujemy 31im(sn) i lim(xn) = 66R. Jeśli ciąg (xn) nie jest rosnący, dowód jest podobny. Przejdźmy teraz do dowodu wystarczalności kryterium Kochia dla zbieżności ciągu (patrz Twierdzenie 6.3), ponieważ konieczność warunku kryterium wynika z Twierdzenia 6.7. Niech ciąg (sn) będzie fundamentalny. Zgodnie z definicją 6.4, mając dowolne € > 0, można znaleźć taką liczbę N(s), że m^N i n^N następują po sobie. Wtedy zakładając m - N, dla Vn > N otrzymujemy € £ Ponieważ rozważany ciąg ma skończoną liczbę elementów o liczbach nieprzekraczających N, to z (6.35) wynika, że ​​podstawowy ciąg jest ograniczony (dla porównania zob. dowód Twierdzenia 6.2 o ograniczoności ciągu zbieżnego ). Dla zbioru wartości ciągu ograniczonego istnieją granice infimum i supremum (patrz Twierdzenie 2.1). Dla zbioru wartości elementów dla n > N oznaczamy te ściany odpowiednio an = inf xn i bjy = sup xn. Gdy N wzrasta, dokładna dolna granica nie maleje, a dokładna górna granica nie wzrasta, tj. . Czy otrzymam system eloasenna? segmenty Zgodnie z zasadą segmentów zagnieżdżonych istnieje wspólny punkt, który należy do wszystkich segmentów. Oznaczmy to przez b. Tak więc, gdy Z porównania (6. 36) i (6.37) w rezultacie otrzymujemy, co odpowiada definicji 6.3 granicy ciągu, tj. 31im(x„) i lim(sn) = 6 6 R. Bolzano zaczął badać podstawowe ciągi. Ale nie miał ścisłej teorii liczb rzeczywistych i dlatego nie udało mu się udowodnić zbieżności ciągu podstawowego. Dokonał tego Cauchy, przyjmując za pewnik zasadę zagnieżdżonych segmentów, którą później potwierdził Kantor. Nazwę Cauchy'ego nadano nie tylko kryterium zbieżności ciągu, ale także ciąg podstawowy nazywany jest często ciągiem Cauchy'ego, a nazwą Cantora jest zasada segmentów zagnieżdżonych. Pytania i zadania 8.1. Udowodnij, że: 6.2. Podaj przykłady ciągów niezbieżnych, których elementy należą do zbiorów Q i R\Q. 0,3. W jakich warunkach wyrazy ciągu arytmetycznego i geometrycznego tworzą ciąg malejący i rosnący? 6.4. Udowodnij zależności wynikające z tabeli. 6.1. 6.5. Skonstruuj przykłady ciągów dążących do nieskończonych punktów +oo, -oo, oo oraz przykład ciągu zbiegającego się do punktu 6 ∈ R. c.e. Czy nieograniczony ciąg nie może być b.b.? Jeśli tak, to podaj przykład. w 7. Skonstruuj przykład ciągu rozbieżnego składającego się z elementów dodatnich, który nie ma ani skończonej, ani nieskończonej granicy. 6.8. Udowodnij zbieżność ciągu (n) określonego wzorem rekurencyjnym sn+i = sin(xn/2) pod warunkiem „1 = 1”. 6.9. Udowodnij, że lim(xn)=09 jeśli sn+i/xn-»g€)