разсъждение, при което се извършва преход според правилата от твърдение или система от твърдения към твърдение или система от твърдения. Към логическия извод обикновено се налагат следните изисквания (заедно или поотделно): 1) правилата за преход трябва да възпроизвеждат отношението на логическата последователност (една или друга негова разновидност); 2) преходите в логическото заключение трябва да се извършват въз основа на отчитане само на синтактичните характеристики на изявления или системи от изявления.
В някои случаи изводът е дефиниран по такъв начин, че се поставят ограничения върху използването на определени правила. Например, в аксиоматичните изчисления, които са варианти на класическата предикатна логика от първи ред и съдържат сред правилата за извод само modus ponens и правилото за обобщение, логическият извод често се дефинира по такъв начин, че се налага ограничение върху използването на правилото за обобщение: всяко приложение на правилата за обобщение в е такова, че променливата, според която обобщението в това приложение на правилото за обобщение не е включена в никоя предпоставка, предхождаща долната формула на това приложение на правилото за обобщение. Целта на това ограничение е да осигури редица логически полезни свойства на извода (например изпълнението на теоремата за прости форми на дедукция). Има дефиниции на логически изводи (както за аксиоматични, така и за други видове изчисления), които (1) определят логическо заключение не само от набор от предпоставки, но позволяват други форми на организация на предпоставките (например списъци или последователности), (2) структурират заключението не само линейно, но, например, под формата на дърво, (3) имат ясно изразен индуктивен характер; в този случай индуктивното определяне на заключението може да се извърши както според една променлива (например по дължината на изхода), така и според няколко променливи (например според дължината на логическото заключение и брой на неговите предпоставки), (4) съдържат формализиране на зависимостта между формулите в логическия извод и много други дефиниции на логическия извод, обусловени от други методи за формализиране и аксиоматизиране на класически и некласически логически системи. За някои от тях виж чл. Метод на аналитични таблици. Семиотика, Смятане на последователности.
Отлично определение
Непълна дефиниция ↓
логически изход
ЛОГИЧЕСКИ ИЗХОД - обосновавам се,в който по определени правила се извършва преход от твърдения или система от твърдения към твърдение или система от твърдения. Към V. l. Обикновено се представят следните изисквания (наведнъж или поотделно): 1) правилата за преход трябва да възпроизвеждат връзката на логическата импликация (една или друга от нейните разновидности), 2) преходите в V. l. трябва да се извършва въз основа на отчитане само на синтактичните характеристики на изявления или системи от изявления. В съвременната логика V. l. се дефинира за формални системи, в които твърденията са представени чрез формули. Обикновено има три основни типа формални системи: аксиоматични изчисления, естествени изводни изчисления и последователни изчисления. Стандартна дефиниция на V. l. (от набора от формули G) за аксиоматичното смятане S е както следва: V. l. в S от набора от формули Γ има последователност Ar..An от формули в езика за смятане S, така че за всяко A. (1 i n) е изпълнено поне едно от следните три условия: 1) A. е a формула от Γ; 2) А. е аксиома на смятане S; 3) A. е формула, получена от формулата, която я предхожда в редицата A,... A или от формулите, които я предхождат в тази редица, съгласно правилото за извеждане на смятането S. Ако a е V. l. в S от множеството формули Г, то формулите от Г се наричат предпоставки, а самото заключение се нарича V. l. в S от помещения G; ако в същото време A е последната формула на a, тогава a се нарича V. l. в S на формулата A от предпоставките на G. Означението "G | - A" означава, че има V. l. в S на формула А от помещенията на Г.В.л. в S от празен набор от формули се нарича доказателство в S. Нотацията “|- A” означава, че има доказателство в S на формула A. Формула A се казва, че е доказуема в S, ако h A. Като пример, разгледайте аксиоматичното смятане S със стандартната дефиниция на извода, което е вариант на аксиоматизацията на класическото пропозиционална логика.Азбуката на езика L на това смятане съдържа само пропозиционални променливи p, p2,..., P p - - - логически връзки s, - и скоби. Дефиницията на L-формула (формула на езика L) е обичайна: 1) пропозиционалната променлива е L-формула, 2) ако A и B са L-формули, тогава (A 3 B), (- A) са L-формули, 3) нищо друго не е L-формула. Аксиомите Sj са всички L-формули от следните шест типа (и само тези типове): I (Az A), II ((ADB)D((BDC)3(ADC))), III ((AD(BDQ)D ( BD(ADC))), IV ((ADhB))D(BDhA))), V (hhA))DA), VI (((A s B) z A) z A). Единственото правило на смятането Sj е правилото на modus ponens в L: A, (A o B) / B (където A и B са L-формули). Определение на V. l. за S е очевидна спецификация на стандартната дефиниция на V. l., която е дадена по-горе. Последователност ((р1з р2) з (р, з р2)), (((р, з р2) з (Р, = Р2» 3 (Р, = ((Р, е Р 2) е Р2))) (P i 3 ( (Р, 3 Р 2) 3 Р2)) Pi´ ((р, з р2) з р2) L-формулите са V. l. в S, L-формулите ((р; з р2) з р2) от pj. Наистина, първият член на тази последователност е аксиома от тип I, вторият член на тази последователност е аксиома от тип III, третият член на тази последователност се получава от първия и втория член на тази последователност според modus ponens правило в L, четвъртият член на тази последователност е L-формулата на, петият член на тази последователност се получава от четвъртия и третия член на тази последователност съгласно правилото на modus ponens в L. И така, p, (- 51((p,sp2)sp2). В редица случаи V. l. се дефинира по такъв начин, че използването на определени правила в него е ограничено. Например за някои аксиоматични изчисления, които са варианти на аксиоматизацията на класическото предикатна логикапърви ред и съдържащ сред правилата за извод правило за обобщение, V. l. понякога се определя по такъв начин, че се налага ограничение върху използването на правилото за обобщение, забраняващо използването му във V. l. правила за обобщение за променлива, включена в поне една предпоставка на даден V. l. Известен V. l. (както за аксиоматични изчисления, така и за изчисления от други видове) не само от набори от формули, но и от други системи от формули (например от последователности от формули, от списъци с формули). Ние изучаваме V. l., които нямат линейна структура (всеки V. l., който отговаря на стандартната дефиниция на V. l., има линейна структура, защото е последователност от формули), но има например дървовидна структура. Считат се V. l., които съдържат формализиране на зависимостите между формулите, включени в тях, и много други V. l. Наличието на голям брой разновидности на V. l. поради както множеството логики, така и разнообразието от проблеми, решавани по време на тяхната формализация. В.М. Попов
Когато се прави заключение, е удобно да се представят правилата за въвеждане и премахване на логически връзки по същия начин, както правилата за извод:
Правило 1.Ако предпоставките $F_1$ и $F_2$ имат значението “и”, то тяхната конюнкция е вярна, т.е.
$$\frac(F_1 ; F_2)((F_1\&F_2))$$
Този запис, ако предпоставките $F_1$ и $F_2$ са верни, предоставя възможността за въвеждане на логическа връзка на връзка в заключението; това правило е идентично с аксиома A5 (виж);
Правило 2.Ако $(F_1\&F_2)$ има стойност „и“, тогава подформулите $F_1$ и $F_2$ са верни, т.е.
$$\frac((F_1\&F_2))(F_1) \: и \: \frac((F_1\&F_2))(F_2)$$
Тази нотация, ако $(F_1\&F_2)$ е вярна, осигурява възможността за премахване на логическата връзка на връзката в заключението и разглеждане на истинските стойности на подформулите $F_1$ и $F_2$; това правило е идентично с аксиомите A3 и A4;
Правило 3.Ако $F_1$ има стойност „и“, а $(F_1\&F_2)$ има стойност „l“, тогава подформулата $F_2$ е невярна, т.е.
$$\frac(F_1;\left\rceil\right. \!\!(F_1\&F_2))( \left\rceil\right. \!\!F_2)$$
Този запис, ако $(F_1\&F_2)$ е невярно и една от подформулите е вярна, предоставя възможност за премахване на логическата връзка на връзката в заключението и считане на стойността на втората подформула за невярна;
Правило 4.Ако поне една предпоставка $F_1$ или $F_2$ е вярна, тогава тяхната дизюнкция е вярна, т.е.
$$\frac(F_1)( (F_1\vee F_2)) \: или \: \frac(F_2)( (F_1\vee F_2))$$
Тази нотация, ако поне една подформула $F_1$ или $F_2$ е вярна, осигурява възможността за въвеждане на логическа връзка на дизюнкция в заключението; това правило е идентично с аксиомите A6 и A7;
Правило 5.Ако $(F_1\vee F_2)$ има стойност „и“ и една от подформулите $F_1$ или $F_2$ има стойност „l“, тогава втората подформула $F_2$ или $F_1$ е вярна, т.е.
$$\frac((F_1\vee F_2); \left\rceil\right. \!\!F_1 )( (F_2) \: или \: \frac((F_1\vee F_2); \left\rceil\right . \!\!F_2 )( (F_1)$$
Тази нотация, ако $(F_1\vee F_2)$ е вярна, осигурява възможността за премахване на логическата връзка на дизюнкцията в заключението и разглеждане на истинските стойности на подформулите $F_1$ или $F_2$;
Правило 6.Ако подформулата $F_2$ има стойността "и", тогава формулата $(F_1\rightarrow F_2)$ е вярна за всяка стойност на подформулата $F_1$, т.е.
$$\frac(F_2)( (F_1\дясна стрелка F_2))$$
Тази нотация, с истинска стойност $F_2$, осигурява възможността за въвеждане на импликация в заключението на логическа връзка за всяка стойност на подформулата $F_1$ („истина от всичко“); това правило е идентично с аксиома 1;
Правило 7.Ако подформулата $F_1$ има стойност „l“, тогава формулата $(F_1\rightarrow F_2)$ е вярна за всяка стойност на подформулата $F_2$, т.е.
$$\frac(\left\rceil\right. \!\!F_1 )( (F_1\rightarrow F_2))$$
Тази нотация, ако стойността на $F_1$ е невярна, осигурява възможността за въвеждане на логическа връзка на импликация в заключението за всяка стойност на подформулата $F_2$ („всичко от невярно“);
Правило 8.Ако формулата $(F_1\rightarrow F_2)$ има стойността „и“, тогава формулата $(\left\rceil\right. \!\!F_2\rightarrow \left\rceil\right. \!\!F_1) $ е вярно, т.е.
$$\frac((F_1\rightarrow F_2) )( (\left\rceil\right. \!\!F_2\rightarrow \left\rceil\right. \!\!F_1))$$
Този запис, с истинска стойност $(F_1\rightarrow F_2)$, определя възможността за размяна на полюсите на импликацията, като същевременно се променят техните стойности; това е законът на противоположността;
Правило 9.Ако формулата $(F_1\rightarrow F_2)$ има стойността „и“, тогава формулата $((F_1\vee F_3)\rightarrow (F_2\vee F_3)$ е вярна за всяка стойност на $F_3$, т.е.
$$\frac((F_1\rightarrow F_2) )(((F_1\vee F_3)\rightarrow (F_2\vee F_3)) $$
Този запис, с истинска стойност $(F_1\rightarrow F_2)$, определя способността за извършване на операция на дизюнкция за всяка стойност на формулата $F_3$ над всеки полюс на импликацията; това правило е идентично с аксиома A11.
Правило 10.Ако формулата $(F_1\rightarrow F_2)$ има стойността „и“, тогава формулата $((F_1\&F_3)\rightarrow (F_2\&F_3)$ е вярна за всяка стойност на $F_3$, т.е.
$$\frac((F_1\дясна стрелка F_2) )(((F_1\&F_3)\дясна стрелка (F_2\&F_3))$$
Този запис, с истинска стойност $(F_1\rightarrow F_2)$, определя способността за извършване на операцията на свързване за всяка стойност на формулата $F_3$ над всеки полюс на импликацията; това правило е идентично с аксиома A10.
Правило 11.Ако формулите $(F_1\rightarrow F_2)$ и $(F_2\rightarrow F_3)$ имат стойност „и“, то формулата $(F_1\rightarrow F_3)$ е вярна, т.е.
$$\frac((F_1\rightarrow F_2); (F_2\rightarrow F_3) )((F_1\rightarrow F_3))$$
Този запис, с истинската стойност на $(F_1\rightarrow F_2)$ и $(F_2\rightarrow F_3)$, предоставя възможността за формиране на импликацията $(F_1\rightarrow F_3)$ (законът на силогизма); това правило е идентично с аксиома A2;
Правило 12.Ако формулите $F_1$ и $(F_1\rightarrow F_2)$ имат стойност „и“, тогава формулата $F_2$ е вярна, т.е.
$$\frac(F_1; (F_1\дясна стрелка F_2) )( F_2)$$
Този запис, предвид истинската стойност на предпоставката $F_1$ и импликацията $(F_1\rightarrow F_2)$, ви позволява да премахнете логическата връзка на импликацията и да определите истинската стойност на заключението $F_2$;
Правило 13.Ако формулите са $\left\rceil\right. \!\!F_2 и (F_1\rightarrow F_2)$ имат значението "и", тогава формулата $\left\rceil\right е вярна. \!\!F_1$, т.е.
$$\frac(\left\rceil\right. \!\!F_2; (F_1\rightarrow F_2) )( \left\rceil\right. \!\!F_1)$$
На този запис е дадена истинската стойност на предпоставката $\left\rceil\right. \!\!F_2$ и импликации $(F_1\rightarrow F_2)$ ви позволява да премахнете логическата връзка на импликацията и да определите истинската стойност на заключението $\left\rceil\right. \!\!F_1$;
Правило 14.Ако формулите $(F_1\rightarrow F_2)$ и $(F_2\rightarrow F_1)$ имат стойност „и“, то формулата $(F_1\leftrightarrow F_2)$ е вярна, т.е.
$$\frac((F_1\дясна стрелка F_2); (F_2\дясна стрелка F_1) )( ((F_1\лява дясна стрелка F_2))$$
Този запис с истинската стойност на $(F_1\rightarrow F_2)$ и $(F_2\rightarrow F_1)$ ви позволява да въведете връзка за логическа еквивалентност и да определите стойността на формулата $(F_1\leftrightarrow F_2)$;
Правило 15.Ако формулата $(F_1\leftrightarrow F_2)$ има стойността "и", тогава формулите $(F_1\rightarrow F_2)$ и $(F_2\rightarrow F_1)$ са верни, т.е.
$$\frac((F_1\leftrightarrow F_2) )( (F_1\rightright F_2) ) \: и \: \frac((F_1\leftrightarrow F_2) )( (F_2\rightright F_1) )$$
Този запис с истинската стойност на $(F_1\leftrightarrow F_2)$ ви позволява да премахнете логическата връзка на еквивалентността и да определите истинската стойност на формулите $(F_1\rightarrow F_2)$ и $(F_2\rightarrow F_1) $.
Свойствата на основните понятия са разкрити в аксиоми- предложенията се приемат без доказателства.
Например в училищната геометрия има аксиоми: „през всякакви две точки можете да начертаете права линия и само една“ или „права линия разделя равнина на две полуравнини“.
Системата от аксиоми на всяка математическа теория, разкриваща свойствата на основните понятия, дава техните определения. Такива определения се наричат аксиоматичен.
Свойствата на понятията, които трябва да бъдат доказани, се наричат теореми, последствия, знаци, формули, правила.
Докажете теоремата АIN- това означава да се установи по логичен начин, че всеки път, когато дадено свойство е удовлетворено А, имота ще бъде изпълнен IN.
Доказателствов математиката наричат крайна последователност от твърдения на дадена теория, всяко от които е или аксиома, или се извежда от едно или повече твърдения на тази последователност според правилата на логическото заключение.
В основата на доказателството стои разсъждението – логическа операция, в резултат на която от едно или повече свързани по смисъл изречения се получава изречение, съдържащо нови знания.
Като пример, разгледайте разсъжденията на ученик, който трябва да установи връзката „по-малко от“ между числата 7 и 8. Ученикът казва: „7< 8, потому что при счете 7 называют раньше, чем 8».
Нека разберем на какви факти се основава заключението, получено в този аргумент.
Има два такива факта: Първо: ако броят Апри броене се извикват числата преди b, Че а< b. Второ: 7 се извиква по-рано от 8 при броене.
Първото изречение има общ характер, тъй като съдържа общ квантор – нарича се обща предпоставка. Второто изречение касае конкретните числа 7 и 8 - нарича се частно помещение. От две предпоставки се получава нов факт: 7< 8, его называют заключением.
Между предпоставките и заключението има известна връзка, благодарение на която те съставляват аргумент.
Извиква се аргумент, в който има импликативна връзка между предпоставките и заключението дедуктивен.
В логиката вместо термина "разсъждение" по-често се използва думата "извод".
Извод- това е начин за получаване на нови знания въз основа на някои съществуващи знания.
Изводът се състои от предпоставки и заключение.
Колети- съдържат първоначални знания.
Заключение- това е твърдение, съдържащо ново знание, получено от първоначалното.
По правило заключението се отделя от предпоставките с думите „следователно“, „означава“. Извод с предпоставки Р 1, Р 2, …, рни заключение Рще го запишем във вида: или (Р 1, Р 2, …, рn) Р.
Примери изводи: а) Брой а =b.Номер b = c. Следователно броят a = c.
б) Ако числителят в една дроб е по-малък от знаменателя, тогава дробта е правилна. В дроб числителят е по-малък от знаменателя (5<6) . Следователно фракцията - правилно.
в) Ако вали, значи на небето има облаци. В небето има облаци, следователно вали.
Изводите могат да бъдат верни или неверни.
Изводът се нарича правилноако формулата, съответстваща на неговата структура и представляваща връзка от предпоставки, свързани със заключението чрез импликационен знак, е идентично вярна.
За това за да се определи дали заключението е правилно, продължете както следва:
1) формализира всички предпоставки и заключения;
2) запишете формула, представляваща връзка от помещения, свързани с импликационен знак със заключение;
3) съставете таблица на истината за тази формула;
4) ако формулата е идентично вярна, тогава заключението е правилно; ако не, тогава заключението е неправилно.
В логиката се смята, че правилността на заключението се определя от неговата форма и не зависи от конкретното съдържание на твърденията, включени в него. И в логиката се предлагат правила, следвайки които могат да се изградят дедуктивни заключения. Тези правила се наричат правила за умозаключениеили модели на дедуктивно разсъждение.
Има много правила, но най-често използваните са следните:
1.
![]() - правило за сключване;
- правило за сключване;
2.
![]() - правило за отрицание;
- правило за отрицание;
3.
![]() - правилото на силогизма.
- правилото на силогизма.
Да дадем пример изводи, направени отправило изводи:„Ако записът на номер хзавършва с число 5, това число хразделена на 15. Писане на число 135 завършва с число 5 . Следователно броят 135 разделена на 5 ».
Общата предпоставка в това заключение е твърдението „ако О),Че B(x)", Където О)- това е "запис на номера" хзавършва с число 5
“, А B(x)- "номер хразделена на 5
" Конкретна предпоставка е твърдение, което се получава от условието на общата предпоставка, когато
х = 135(тези. A (135)). Заключението е твърдение, извлечено от B(x)при х = 135(тези. V(135)).
Да дадем пример за заключение, направено по правилото негативи:„Ако записът на номер хзавършва с число 5, това число хразделена на 5 . Номер 177 не се дели на 5 . Следователно не завършва с число 5 ».
Виждаме, че в това заключение общата предпоставка е същата като в предишното, а частната е отрицанието на твърдението „брой 177 разделена на 5 "(т.е.). Изводът е отрицанието на изречението „Писане на число 177 завършва с число 5 "(т.е.).
И накрая, нека помислим пример за извод, основан на правило за силогизъм: „Ако броят хмногократни 12, тогава е кратно 6. Ако броят хмногократни 6 , тогава е кратно 3 . Следователно, ако броят хмногократни 12, тогава е кратно 3 ».
Това заключение има две предпоставки: „ако О),Че B(x)" и ако B(x),Че C(x)“, където A(x) е „числото хмногократни 12 », B(x)- "номер хмногократни 6 " И C(x)- "номер хмногократни 3 " Заключението е твърдение „ако О),Че C(x)».
Нека проверим дали следните изводи са верни:
1) Ако четириъгълникът е ромб, тогава неговите диагонали са взаимно перпендикулярни. ABCд- ромб Следователно неговите диагонали са взаимно перпендикулярни.
2) Ако числото се дели на 4 , тогава се разделя на 2 . Номер 22 разделена на 2 . Поради това се разделя на 4.
3) Всички дървета са растения. Борът е дърво. Това означава, че борът е растение.
4) Всички ученици от този клас отидоха на театър. Петя не беше в театъра. Следователно Петя не е ученичка в този клас.
5) Ако числителят на дроб е по-малък от знаменателя, тогава дробта е правилна. Ако една дроб е правилна, тогава тя е по-малка от 1. Следователно, ако числителят на една дроб е по-малък от знаменателя, тогава дробта е по-малка от 1.
Решение: 1) За да разрешим въпроса за правилността на извода, нека идентифицираме неговата логическа форма. Нека въведем следната нотация: C(x)- "четириъгълник" х- ромб", B(x)- „в четириъгълник хдиагоналите са взаимно перпендикулярни." Тогава първата предпоставка може да се запише като:
C(x) B(x),второ - C(a),и заключението Б(а).
Така формата на това заключение е: ![]() . Изгражда се по правилото на заключението. Следователно това разсъждение е правилно.
. Изгражда се по правилото на заключението. Следователно това разсъждение е правилно.
2) Нека въведем обозначението: О)- "номер хразделена на 4
», B(x)- "номер хразделена на 2
" След това записваме първата предпоставка: О)B(x),второ Б(а),и заключението е А(а).Заключението ще приеме формата: ![]() .
.
Няма такава логическа форма сред известните. Лесно е да се види, че и двете предпоставки са верни, а заключението е невярно.
Това означава, че това разсъждение е неправилно.
3) Нека въведем някои обозначения. Позволявам О)– „Ако хдърво", B(x) - « храстение“. Тогава колетите ще приемат формата: О)B(x), A(a),и заключението Б(а).Нашето заключение е изградено във формата: ![]() - правила за сключване.
- правила за сключване.
Това означава, че нашите разсъждения са структурирани правилно.
4) Нека О) - « х- ученици от нашия клас, B(x)- „ученици хотиде на театър." Тогава колетите ще бъдат както следва: О)B(x),, и заключението.
Това заключение се основава на правилото за отрицание:
![]() - това означава, че е правилно.
- това означава, че е правилно.
5) Нека идентифицираме логическата форма на умозаключението. Позволявам A(x) -"числител на дроб хпо-малко от знаменателя." B(x) - “фракция х- правилно." C(x)- "фракция" хпо-малко 1 " Тогава колетите ще приемат формата: О)B(x), B(x) C(x),и заключението О)C(x).
Нашето заключение ще има следната логическа форма: ![]() - правилото на силогизма.
- правилото на силогизма.
Това означава, че това заключение е правилно.
В логиката се разглеждат различни начини за проверка на правилността на изводите, включително анализ на коректността на изводите с помощта на кръгове на Ойлер.Извършва се по следния начин: заключението се записва на теоретико-множествен език; изобразяват предпоставки на кръгове на Ойлер, като ги считат за верни; те гледат дали заключението винаги е вярно. Ако да, тогава те казват, че умозаключението е конструирано правилно. Ако е възможен чертеж, от който е ясно, че заключението е невярно, тогава те казват, че заключението е неправилно.
Таблица 9
Словесно формулиране на изречението | Нотиране на теоретико-множествен език | Изображение върху кръгове на Ойлер | ||
Всякакви неща АИма IN |
| |||
някои АИма IN някои АДа не се яде IN | ||||
Нито един АДа не се яде IN |
АИма А | ||
АДа не се яде А |
Нека покажем, че изводът, направен съгласно правилото за извод, е дедуктивен. Първо, нека напишем това правило на теоретико-множествен език.
Пакет О)B(x)може да се напише като ТАтелевизор, Където ТАИ телевизор- множества истинност от пропозиционални форми О)И B(x).
Частен колет A(a)означава, че АТА,и заключението Б(а)показва че Ателевизор.
Целият извод, конструиран съгласно правилото за извод, ще бъде написан на теоретико-множествен език, както следва: ![]() .
.
| ||||
| ||||
Ориз. 58.
Примери.
1. Правилно ли е заключението „Ако едно число завършва на число“? 5, тогава числото се дели на 5. Номер 125 разделена на 5. Следователно, писане на числото 125 завършва с число 5 »?
Решение:Това заключение се прави по схемата ![]() , което съответства на
, което съответства на ![]() . Няма позната на нас такава схема. Нека да разберем дали това е правило за дедуктивно заключение?
. Няма позната на нас такава схема. Нека да разберем дали това е правило за дедуктивно заключение?
Нека използваме кръговете на Ойлер. На теоретико-множествен език
Полученото правило може да бъде написано по следния начин:
![]() . Нека изобразим множествата върху окръжности на Ойлер ТАИ телевизори обозначават елемента Аот много телевизор.
. Нека изобразим множествата върху окръжности на Ойлер ТАИ телевизори обозначават елемента Аот много телевизор.
Оказва се, че може да се съдържа в комплект ТА,или може да не му принадлежи (фиг. 59). В логиката се смята, че такава схема не е правило за дедуктивно заключение, тъй като не гарантира истинността на заключението.
Този извод не е правилен, тъй като е направен по схема, която не гарантира истинността на разсъжденията.
| |||
Ориз. 59.
б) Всички глаголи отговарят на въпроса „какво да правя?“ или „какво трябва да направя?“ Думата "метличина" не отговаря на нито един от тези въпроси. Следователно "метличина" не е глагол.
Решение:а) Нека напишем това заключение на теоретико-множествен език. Нека означим с А- много студенти от Педагогическия факултет, чрез IN- много ученици, които са учители, чрез СЪС- много студенти над 20 години.
Тогава заключението ще приеме формата: ![]() .
.
Ако изобразим тези множества на кръгове, тогава са възможни 2 случая:
1) комплекти А, Б, Впресичат се;
2) комплект INпресича се с много СЪСИ а,и много Апресича IN, но не се пресича с СЪС.
б) Нека означим с Амного глаголи и чрез INмного думи, които отговарят на въпроса "какво да правя?" или „какво трябва да направя?“
Тогава заключението може да се напише по следния начин:
Нека да разгледаме няколко примера.
Пример 1. Ученикът е помолен да обясни защо числото 23 може да бъде представено като сбор от 20 + 3. Той разсъждава: „Числото 23 е двуцифрено. Всяко двуцифрено число може да бъде представено като сбор от цифри. Следователно 23 = 20 + 3."
Първото и второто изречение в това заключение са предпоставки, а едното от общ характер е твърдението „всяко двуцифрено число може да бъде представено като сбор от цифрови членове“, а другото е конкретно, то характеризира само числото 23 - то е двуцифрено. Заключението - това изречение, което идва след думата "следователно" - също е лично по природа, тъй като се отнася до конкретното число 23.
Изводите, които обикновено се използват при доказване на теореми, се основават на концепцията за логическа импликация. Освен това от дефиницията на логическата импликация следва, че за всички стойности на пропозиционалните променливи, за които първоначалните твърдения (предпоставки) са верни, заключението на теоремата също е вярно. Такива заключения са дедуктивни.
В примера, обсъден по-горе, даденото заключение е дедуктивно.
Пример 2. Една от техниките за запознаване на учениците от началното училище с комутативното свойство на умножението е следната. Използвайки различни нагледни средства, учениците, заедно с учителя, установяват, че напр. 6 3 = 36, 52 = 25. След това въз основа на получените равенства правят извода: за всички естествени числа аИ bравенството е вярно ab = ba.
В това заключение предпоставките са първите две равенства. Те твърдят, че такова свойство е валидно за конкретни естествени числа. Изводът в този пример е общо твърдение - комутативното свойство на умножението на естествени числа.
В това заключение предпоставките от определено естество показват това някоиЕстествените числа имат следното свойство: пренареждането на множителите не променя произведението. И на тази основа се стигна до заключението, че всички естествени числа имат това свойство. Такива изводи се наричат непълна индукция.
тези. за някои естествени числа може да се твърди, че сборът е по-малък от произведението им. Това означава, че въз основа на факта, че някои числа имат това свойство, можем да заключим, че всички естествени числа имат това свойство:
Този пример е пример за аналогично разсъждение.
Под аналогияразбирайте заключение, при което въз основа на сходството на два обекта по някои характеристики и наличието на допълнителна характеристика в един от тях се прави заключение за наличието на същата характеристика в другия обект.
Заключението по аналогия е по природа на предположение, хипотеза и следователно се нуждае или от доказателство, или от опровержение.
Структурата на всяко умозаключение включва предпоставки, заключение (следствие) и заключение. Предпоставките на едно заключение са първоначалните съждения, от които се извлича ново съждение. Заключение (последствие) е ново съждение, получено логически от предпоставките. Заключението е логически преход от предпоставки към заключение.
Споделете работата си в социалните мрежи
Ако тази работа не ви подхожда, в долната част на страницата има списък с подобни произведения. Можете също да използвате бутона за търсене
ТЕМА 5. ДЕДУКТИВНИ ИЗВОДИ. ИЗВОДИ ОТ ПРОСТИ СЪЖДЕНИЯ (ИЗВОДИ НА ПРЕДИКАТНАТА ЛОГИКА)
Основни въпроси: Понятието умозаключение. Видове изводи. Дедуктивно разсъждение от прости твърдения. Преки изводи и техните видове. Прост категоричен силогизъм. Ентимема.
Ключови термини и понятия
ЗАКЛЮЧЕНИЕ форма на мислене чрез катО рояк от едно или повече съждения, основани на определени правила за умозаключениеО Да, получава се нова присъда.
Структурата на всяко умозаключение включва предпоставки, заключенияЮ прочит (последствие) и заключение.Предпоставки за извод, начални твърдения твърдения, от които се извлича ново съждение.Заключение (последствие) това е нова преценка, получена логически от предпоставки. INвода това е логичен преход от помещения към zи ключът.
Например: „Всички риби дишат с хриле (1), нито един делфин не диша с хриле (2), следователно нито един делфин не е риба (3).“ В това заключение съжденията (1,2) са предпоставки и преценкае ция (3) заключение. При анализ на заключението на предпоставките и изводитеЮ Прието е показанията да се записват отделно, като се поставят едно под друго. Заключението се записва под хоризонтална линия, която го отделя от предпоставките и указва логическата последица. В съответствие с това може да се направи горното заключениено го изразете така:
Всички риби дишат през хрилете.
Нито един делфин не диша през хрилете a mi.
Никой делфин не е пбитка.
КЛАСИФИКАЦИЯ НА ИЗВОДИТЕ
Изводи
Дедуктивен Недедуктивенв нов
Изводи Изводи Индуктивни изводию
от прости съждения - от сложни съждения - заключения - по аналогия
deniya (констатации deniya (заключения niya
логика пред- логика високо-
котка) имена)
Изводи от прости твърдения
(изводи на предикатната логика)
Директно Опосредованов
Трансформация Проста категоричнаески
Обжалване на sill o gizm
Контраст с предикат
Изводи с помощта на логически квадрат
Изводи от съждения с отношения
Изводи от сложни съждения
(заключения на пропозиционалната логика)
Чисто условни заключения
Условни разделителни (лематични) изводи
ДЕДУКТИВНО ВЛИЯНИЕ заключение, при което връзката между предпоставките и извода е логическа закономерност, поради което от верни предпоставки по необходимост следва верен извод. С други думи, това е заключение, в което съществува логическа връзка между предпоставките и заключението. В процеса на разсъждение заключенията, които не са дедуктивни, понякога се бъркат с дедуктивни. Това са т.нарнеправилно дедуктивно разсъждение. Всъщност дедуктивно разсъждение се наричаправилно . При правилното дедуктивно разсъждение заключението също се наричалогично следствие.
ЛОГИЧНО СЛЕДСТВИЕ съждение, което не може да бъде невярно, ако е изведено от истински предпоставки. С други думи, присъдата IN е логично следствие от предложениетоА , ако импликация (А Б ) е идентично истинската формапри лой, т.е. закон на логиката.
ПРЯКО ЗАКЛЮЧЕНИЕ дедуктивно разсъждение, при което заключение се извежда само от една предпоставка.
ТРАНСФОРМАЦИЯ вид пряко умозаключение, в заключението на което субектът е субект на първоначалното съждение (предпоставка), а предикатът концепция, която противоречи на предикатната позал ki, в същото време качеството на пратката се променя, количественият характерИ стилът на преценка не се променя. В резултат на трансформацията възниква съждение, което е еквивалентно на първоначалното. Всички подлежат на трансформацияд три вида присъди: A, E, I, O.
Логически форми на изводи на трансформация:
О: _____ Всички S са P_ ____.
Не S не е P
E: Никое S не е P.
Всички S не са P
Аз: ___ Някои S са P ___ .
Някои S не са P
Някои Ss не са Ps
Примери:
А : Всички престъпления са наказуеми. Следователно нито едно престъпление не е ненаказано деяние.
д : Никой кит не диша през хриле. Следователно всички китове саИ Вотиви, които не дишат с хриле.
аз : Някои спортисти победители в състезанието. Следователно някои спортисти не се хранят победители в състезаниетои ния.
ОТНОСНО : Някои ценни книжа не са акции. Следователно някои ценни книжа не са акции.
РАЗГОВОР пряко заключение, в заключението на което субектът е предикат, а предикатът субект на първоначалното съждение (предпоставка), качеството на съждението не се променя. Количествените характеристики на заключението могат да бъдат различни в сравнение с количествените характеристики на помещенията. Това зависи от разпределението на термините в помещението. Обжалването се подчинява на правилото: термин, който не е разпределен в предпоставката, не може да бъде разпределен в заключението.
Има два вида обжалване:прости (или чисти) и ограничение на обработката. просто(или чисто ) обжалването ще бъде, когато и двата термина са разпределени в помещението ( S+, P+ ) или и двете не са разпределени ( S - , P - ). Справяне с ограничениетоще бъде, когато субектът е разпределен в помещението ( S+ ), а предикатът не е разпределен ( R - ), или обратното, темата не се разпространява (С- ), а предикатът е разпределен ( P +).
На обжалване подлежат три вида решения: A, E, I. Съдебно решение тип O (частично отрицателно) не се прилага.
Логически форми на обжалване:
A: a) ___ Всички S + са P - ____; б) Всички S + са P + .
Някои P са S + Всички P + са S +
E: Никое S+ не е P+.
Нито един P+ не е S+
I: а) Някои S - са P - ; b) Някои S - са P + .
Някои P - са S - Всички P + са S -
Примери:
О: а) Всички цигулари музиканти. Следователно някои музиканти са цигулари.
б) Всички престъпления са престъпления. Следователно всички престъпни деяния са престъпления.
E: Никоя акция не е облигация. Следователно нито една облигация не е акция.
аз: а) Някои свидетели са дали верни показания. Следователно някои лица, които са дали верни показания, са свидетели.
б) Някои градове столици на държави. Следователно, цялата масаИ Градовете на държавите са си градове.
ПРОТИВОПОСТАВЯНЕ НА ПРЕДИКАТ пряко заключение, в заключението на което субектът е понятие, което противоречи на предиката на предпоставката, а предикатът на субекта на предпоставката, докато заключението и предпоставката са различни по качество. С други думи, противопоставянето на предикат се извършва чрез последователно прилагане на трансформацията на първоначалното съждение (предпоставки) и след това инверсия на полученото съждение. Изводът, получен чрез контрастиране на предиката, зависи от количеството и качеството на помещенията. Три вида съждения се противопоставят на предиката:А, Д, О. Особено положително решение (аз ) не се противопоставя на предикат.
Логически форми на изводи в противопоставяне на предикат:
О: ______ Всички S са P__ ____.
Нито едно P не е S
E: __ Никое S не е P__.
Някои нямат P имат S
A: _ Някои S не са P_.
Някои нямат P имат S
Примери:
О: Всички драматурзи писатели,. Следователно никой писателят не е драматург.
д : Никой адвокат не е прокурор. Следователно някои лица, които не са прокурори, са адвокати.
ОТНОСНО : Някои красавици не са актриси. Следователно, nд които не са актрисите имат красотаи пороците.
ИЗВОДИ ПО ЛОГИЧЕСКИЯ КВАДРАТУР преки заключения, които се изграждат на базата на дневникИ ични отношения между прости категорични съждения, фиксирани от схемата на логически квадрат. С други думи, преподавайтеИ показващи логическите връзки между категоричните съждения ( A, E, I, O ), представена от логически квадрат, може да се конструира не-О средство за правене на заключения относно истинността или неистинността на едно твърдение въз основа на истинността или неистинността на друго.
Видове изводи логически квадрат:
1) изводи, основани на връзката на подчинениее ния;
2) изводи, основани на връзката на подпротиворечието (частч съвместимост);
3) изводи, основани на отношението на противоречие (противоположностза лъжата);
4) изводи, основани на отношението на противоречие (прза противоречията).
1) Логически форми на изводи въз основа на подчинени отношенияи мнения:
A I, E O, I A, O E.
Примери:
От истинността на твърдението „Всички кражби са престъпления” следва следнотон валидността на решението „Някои кражби са престъпления“.
От истинността на твърдението „Никоя планета не е комета“ следва истинността на твърдението „Някои планети не са комети“.
От неверността на твърдението „Някои делфини са риби“ следва, чеи стойността на съждението „Всичко е„Риба с перки“.
От фалшивостта на твърдението „Някои цигулари не са музиканти“д показва фалшивостта на твърдението „Нито един цигулар не е музикант“.
2) Логически форми на изводи от отношението на субконтраст: I O, O I.
3) Логически форми на изводи от отношението на противоположност:
A E, E A.
4) Логически форми на изводи от противоречивото отношениеотносно sti:
A O, E I, O A, I E, A O, E I, O A, I E.
ИЗВОДИ ОТ РЕШЕНИЯ С ОТНОШЕНИЯ изводи, основани на свойствата на бинарните отношения. Най-важното от тези свойства преобразуване, симетрия, транси активност. преобразувания: R ab R ba .
Пример. Луганск се намира на север от Одеса, което означава, че Одеса се намира на юг от Луганск.
Логическа форма на умозаключение въз основа на свойствосиметрия: R ab R ba.
Пример . Иван е на същата възраст като Петър, което означава, че Петър е на същата възраст като Иван.
Логическа форма на умозаключение въз основа на свойствотранзитивност: (R ab R bс) R ac.
Пример . Иван е по-възрастен от Петър, а Петър е по-възрастен от Николай, което означава, че Иван е по-възрастен от Николай.
ПРОСТ КАТЕГОРИЧЕН СИЛОГИЗЪМ дедуктивно заключение, при което от две категорични съждения, еднотоР натискане на общ термин, ако правилата са спазени, се показва нова коткае горещо ское решение. Пример за силогизъм:
1. Всички риби дишатб рами.
2. Всички каракуди са риби. _______
3. Всички каракуди дишат през хрилете.
Структура на силогизъм:
Предпоставки на силогизма съдебни решения, от които се извлича ново съдебно решениед ция (в примера за изпращане това са присъди 1, 2). Заключение ново решение твърдението, което се извлича от предпоставките (решение 3). Във всеки первазО gism трябва да има три члена: по-малък, по-голям и среден.В по-малък срок предметът на заключението се нарича (в примера по-малкият термин е „каракуда“).Голям срокпредикатът се наричаЮ чения („дишам с хриле“).Среден сроке термин, който се съдържа в предпоставките, но не се съдържа в заключението („риба“). Второстепенният термин е обозначен с буквата S, по-голям с буквата P, среден с буквата M.
Предпоставките на силогизма също имат специални имена. Предпоставка, съдържаща по-голям член, се наричапо-голям. Предпоставката с по-малък член се наричапо-малко . Традиционно силогизмите първо показватголям пакет и след товапо-малък . Логическа форма на намалено siл Логизмът има формата:
Всички М са Р.
Всички S са M.
Всички S са P.
Аксиома на силогизма позиция, съставляваща правотоР ност на изхода, т.е. логически преход от предпоставки към заключение в категоричен силогизъм. Изглежда така: „Всичко, което се твърди (за T се отрича) за всички обекти от определен клас, задължително се потвърждава (отрича) за всеки обект и всяка част от обекти, принадлежащи към даден классъс су.“
ОБЩИ ПРАВИЛА НА СИЛОГИЗМА правила, предвидениИ необходимо е получаването от истински предпоставки на истинско следствиед действия. Има две групи правила: правила за термини и правила за термини.о синко
Правила за термини: 1) силогизмът трябва да има само три термина; 2) средният срок трябва да бъде разпределен в поне едно от селатас лок; 3) термин, който не е разпределен в предпоставката, не може да бъде разпределенд разделени в ареста.(Възможна грешка:удължаване на срока).
Правила за пратки:1) от две отрицателни предпоставки, както и от две конкретни предпоставки, заключението не следва непременно; 2) ако една от предпоставките е отрицателна или конкретно съждение, тогава заключението трябва да бъдеи но да бъде съответно отрицателно или частично suживот.
ФИГУРА НА СИЛОГИЗМА вид силогизъм в зависимост от позицията на средния терминМ в колети. Има четири фигури, които могат да бъдат схематично изобразени по следния начин:
М Р Р М М Р Р М
С М С М С М С
С Р С Р С Р С Р
I II III IV
Фигура фигура фигура фигура
Специални правила за фигури:
аз фигура: 1. Голяма опаковкаобща преценка.
2. По-малка опаковка утвърдително съждение.
II фигура: 1. Голяма опаковкаобща преценка.
2. Един от колетите отрицателна преценка.
III фигура: 1. По-малък пакет утвърдително съждениед ция.
2. Заключение частна преценка.
IV Фигура: I. Няма общи утвърдителни заключенияи др.
2. Ако опаковката е голяма утвърдително, след това второстепенната предпоставкаобща преценка.
3. Ако един от парцелите отрицателна преценка, тогава голямо nО Връзката трябва да е обща.
МОДУС НА СИЛОГИЗМА разнообразие от силогични фигури в зависимост от количествените и качествени характеристики на картинатас заключване и заключения. Във всяка фигура има 64 режима (разновидности на фигури), а за четирите фигури има 256. Въпреки това, не във всеки режим заключението следва от предпоставките. Наричат се режими, за които се извършва следнотоправилно . Има общо 24 правила b ny режима (19 силни и 5 слаби), шест във всяка фигура (слабите режими са посочени в скобимустак):
Изчислявам AAA, EAE, AII, EIO, (AAI, EAO ); (Горният силогизъмО построени според режима AAA);
II фигура EAE, AEE, EIO, AOO, (EAO, AEO);
III фигура AAI, EAO, IAI, OAO, AII, EIO;
IV фигура AAI, AEE, IAI, EAO, EIO, (AEO).
ЕНТИМЕМ това е съкратен категоричен силогизъм, в който една от предпоставките или изводът са пропуснати. Ent примерИ мемове с липсващата по-малка предпоставка: „Всички газове са втечняеми, знА мамят, ние втечняваме кислорода”; като липсва по-голямата предпоставка: „Кражба престъпление, защото кражбата е престъпление”; с пропуснатия извод: „Всички истински учители обичат децата, но Иванов истински учител." Ентимите се делят направилни и неправилни . Ентимема с липсваща предпоставка се счита заР правилно (правилно), ако 1) може да се възстанови, за да се коригираА vil начин на категоричен силогизъм, 2) възстановен pО препратката ще се окаже вярно предложение. Ентимема с липсващи sА изключението е правилно, ако просто се възстанови към правилата b на категоричния силогизъм z ma.
Да вземем ентимемата: „Скъперничеството заслужава укор, както всеки порок“. Той съдържа заключението: „Скъперничеството заслужава порицание“ (последвано от думата „като“ съкращение „откакто“) и предпоставката: „Всеки порок заслужава порицание“ (изразено е със съкращение). Това е голям пакет, защото включва терминаР („обвинително“) заключение. Въз основа на терминаС („скъперничество“) и терминътМ („порок“) формулираме по-малката предпоставка „порок на алчността“.
Пълният силогизъм изглежда така:
Всеки порок заслужава укор.
Скъперничеството е порок. ___________________
Скъперничеството е осъдително.
Този силогизъм е съставен според модуса AAA първата цифра, което означава, че е правилна. Възстановената второстепенна предпоставка „Сребролюбието е порок“ може да се приеме за вярна. Следователно ентимемата е правилна.
Литература
- Ивин А. А. Практическа логика: цели на упражнението / А.А. Ивин. М.: Про Осветление, 1996. 128 с.
2. Кирилов V.I. Логика: учебник за юридически. университет / В. И. Кирилов, А. А. Старченко. М.:Адвокат, 2004г. 256 стр. гл. 6.
- Демидов И. В. Логика: учебник / И. В. Демидов. М.: ДаШков и К 0, 2004. 348 с. гл. 5.
- Яшин Б. Л. Логически задачи и упражнения/ Б. Л. Яшин. М.: ВЛАДОС, 1996. 224 с. гл. 5.
УПРАЖНЕНИЯ I - X
аз Установете предпоставките и заключението в следните изводи:
1. За да бъде спазен процесуалният ред е необходимоО Важно е при обиска да присъстват поемни лица. Свидетели по делото обаче не са поканени. Това означава, че процесуалният ред не е спазен.
2. Всички талантливи хора имат странности.н Той не е талантлив, защото няма никакви странности.
3. Сред игралните филми има и нецветни, което значи някаквиО Някои игрални филми не са цветни.
4. Ако съдията е жертвата, тогава той не може да участва в разглеждането на това дело. И тъй като този съдия е потърпевшият, това означава, че той не може да участва в разглеждането на това дело.
5. Тъй като всички счетоводители са с икономическо образование, това означава, че сред тези с икономическо образование има и счетоводители.
6. Всички финансисти са икономисти. Това следва от факта, че някои икономисти са финансисти.
II. Конструирайте непосредствени заключения - трансформация, преобразуване, противопоставяне на предиката - от следните предпоставки:
1. Всички силогизми са изводи.
2. Някои заподозрени нямат алиби.
3. Някои ученици са майстори на спорта.
4. Нито един кит не е риба.
5. Всичко разумно е валидно.
6. Нищо разумно не ме озадачава.
7. Някои художници не са били признати приживе.
8. Някои компютри „разбират“ говоримия език.
9. Учението за силогистиката е създадено от Аристотел.
11. Някои депутати са икономисти.
12. Нито един фалшив документ не е доказателство.
III. Конструирайте директни заключения, като използвате „логическия квадрат“:
1. Никой мързелив човек не заслужава похвала.
2. Някои хора не влияят на хода на историята.
3. Всички музиканти са емоционални.
4. Има ученици без средно образование.
5. Някои цветя не са маргаритки.
6. Обвиняемият има право на защита.
7. Някои деца са добри в рисуването.
8. Сред финансистите има много жени.
9. Никой от здравомислещите хора не би се разхождал под дъжда без чадър.
10. Всяко правило има изключение.
IV. Конструирайте непосредствени изводи от релационни предложения, като използвате свойствата на релациите преобразуване, симетрия, транзитивност:
„Луганск се намира на север от Одеса“, „Тази книга е издадена едновременно с тази“, „Мария е съпругата на Иван“, „Обект A е основан преди обект B, обект B е основан преди обект C.“
V. Проверете правилността на следните непосредствени заключения. Посочете вида на преобразуването. Ако има грешка, обяснете причината и направете правилното заключение:
1. Тъй като някои книги са учебници, нито един неучебник не е книга.
2. Някои художници не са били признати приживе, което означава, че има непризнати художници.
3. „A обича B, B обича C. Това означава, че A обича C.“
4. Никой няма право да нарушава законите, което означава, че няма хора сред тези, които имат право да нарушават законите.
5. Някои европейски държави са унитарни. Това означава, че всички унитарни държави са европейски.
6 . Всички мои приятели познават моя характер много добре, което означава, че този, който познава много добре моя характер, е мой приятел.
7 . Всички трудолюбиви хора поемат най-трудните работи. Следователно никой, който не се заема с най-трудната работа, не може да се счита за трудолюбив човек.
VI. В дадените силогизми установете: следствие, главен термин, основна предпоставка, второстепенен термин, второстепенна предпоставка, среден термин. Определете разпределението на термините.
1. Това пълномощно е невалидно, тъй като не посочваА че е изпълнено, но пълномощно, в което не е посочена датата на извършването муР ция, е невалидна.
2. Някои птици не летят, защото всички щрауси са птици и нито един щраус не лети.
3. Някои жени са писателки. Това означава, че сред тези, които обичат цветад вие, има писатели, защото всички жени обичат цветята.
VII. Докажете по три начина: като използвате специални правила за фигури, правила за термини и правила за предпоставки, дали тези силогизми са правилни и заключението истинска присъда.
1. Не всеки, който може да чете, може да напише книга.
Това дете не може да напише книга.
Това дете не може да чете.
2. Всички хора са смъртни.
Всички велики писатели са безсмъртни.
Всички велики писатели не са хора.
3. Лък оръжие на диваците.
Това растение е лук.
Това растение е оръжие на диваците.
4. Всички цветя са растения.
Всички розови растения.
Всички рози са цветя.
5. Някои изречения са прости.
Всички съдебни присъди
Някои предложения са прости изречения.
VIII. Установете фигурата и начина на всеки силогизъм по-долу и на тази основа определете дали те са правилаbnymi:
1. Всички планети в Слънчевата система се въртят около слънцето.
Юпитер се върти около Слънцето в планетарна орбита.
Планета Юпитер от Слънчевата система.
2. Всички делфини плуват.
Всички плувци живеят във вода.
Някои живеещи във водата са делфини.
3. Само хората вярват в края на света.
Няма човек, който да не вярва в хармонията на света.
Никой от тези, които не вярват в хармонията на света, не вярва в края на света.
4. Само тези, които са смели, са достойни за слава.
Някои самохвалци не са смели.
Някои самохвалци не са достойни за слава.
IX. Използвайки кръгови диаграми, определете кои от следните силогизми са правилни:
1. Някои математици имат способността да смятат бързо.
Всички програмисти са математици.
Всички програмисти имат способността да броят бързо.
2. Всички събития имат начало и край.
Всички събития се случват във времето.
Всичко, което се случва във времето, има начало и край.
3. . Някои писатели са жени.
Всички жени обичат да се обличат красиво.
Някои писатели обичат да се обличат красиво.
X. Проверете коректността на следните записиИмем:
1. Всички ученици са културни, защото са грамотни.
2. Този силогизъм има три термина, което означава, че е правилен.
3. Тъй като всички течности са еластични, това означава, че някои метали не са еластични.
4. Като всички егоисти, страхливецът не е щедър.
5. Тъй като всеки мит е символ, ясно е, че легендата за Херкулес също е символ.
6. Говорителят е нарушил закона за тъждеството, тъй като е подменил понятието.
7. „Оригинален, защото мисли“ (А. С. Пушкин за Е. А. Баратински).
83
СТРАНИЦА 78
Други подобни произведения, които може да ви заинтересуват.vshm> |
|||
| 8886. | ДЕДУКТИВНИ ИЗВОДИ. ИЗВОДИ ОТ СЛОЖНИ СЪЖДЕНИЯ (ИЗВОДИ ОТ ЛОГИКАТА НА ТВЪРДЕНИЯТА) | 23,74 KB | |
| УСЛОВНО-КАТЕГОРИЧНО ИЗВОД – заключение, една от предпоставките на което е условна, а втората е категорично съждение. Това заключение има четири режима: два правилни и два вероятни (неправилни). Правилните режими дават надеждни заключения, т.е. от истински предпоставки непременно водят до верни заключения. Правилните режими съответстват на формули - закони на логиката | |||
| 7711. | Констатации от одита и представяне на доклада | 20 KB | |
| Изисквания на МОС за изготвяне на одиторски доклад за финансови отчети с общо предназначение. Отразяване в одиторския доклад на резултатите от проверката на друга информация, свързана с финансовия отчет. Изисквания на МОС за изготвяне на одиторски доклад за финансови отчети с общо предназначение За изготвянето на одиторски доклад МОС предоставя три стандарта: МОС 700 Докладът на независимия одитор за финансови отчети с общо предназначение описва процедурата за изготвяне... | |||
| 16261. | Система от индикатори за евразийска интеграция на EDB: Основни заключения | 54,74 KB | |
| Цели и структура на Системата от индикатори на евразийската интеграция Регионалната интеграция се отнася до процесите на сложна трансформация и се характеризира с интензификация на отношенията между държавите. В същото време идентифицирането на ефективни стратегии в областта на интеграцията изисква създаването на система за цялостен мониторинг и оценка на текущите процеси на взаимодействие между страните в икономическата, политическата и... | |||
| 8883. | Съждението като форма на мислене. Преценка и предложение. Видове прости съждения и тяхната структура | 42,17 KB | |
| СЪЖДЕНИЕ Основни въпроси: Съждението като форма на мислене. Преценка и предложение. Ключови термини и понятия ПРЕЦЕНКА форма на мислене или мисъл, в която се потвърждава или отрича връзката между обект и неговото свойство, връзката между обекти или съществуването на обект. В езика преценката обикновено се изразява с декларативно изречение. | |||
| 8890. | ПРЕДМЕТ И ЗНАЧЕНИЕ НА ЛОГИКАТА. ЕЗИК НА ЛОГИКАТА | 21,87 KB | |
| Предмет на формалната логика. Азбука на символите в езика на пропозиционалната логика и логиката на предикатите. Изводът е форма на мислене, при която от едно или повече съждения, наречени предпоставки на извод, въз основа на определени правила на логиката, се получава ново съждение като следствие от заключение. | |||
| 8887. | НЕДЕДУКТИВНИ ИЗВОДИ | 22,32 KB | |
| Извод по аналогия. Ключови термини и понятия НЕДЕДУКТИВНО ВЛИЯНИЕ заключение, при което връзката между предпоставките и заключението не е логически закон и при което истинността на предпоставките не гарантира истинността на заключението. Недедуктивното заключение обикновено не произвежда надеждно, а само вероятностно правдоподобно проблематично заключение, докато заключението може да съдържа нова информация, която не е била в помещенията. Недедуктивното заключение също се нарича вероятностно или правдоподобно. | |||
| 136. | Основни видове прости фрази | 6,2 KB | |
| По правило простите фрази са двусловни. Простите фрази включват фрази, които съдържат аналитични форми на думата, например: Ще говоря откровено. Семантично простите също включват фрази, в които зависимият компонент е синтактично или фразеологично единство, несвободна фраза, например: нисък мъж, работещ небрежно, момиче на шестнадесет години. | |||
| 9438. | Изчисляване на прости и сложни постояннотокови вериги | 94,42 KB | |
| Целта на изчисляването на електрическа верига с постоянен ток е да се определят някои параметри въз основа на първоначалните данни, от условията на проблема. На практика се използват няколко метода за изчисляване на прости вериги. Един от тях се основава на използването на еквивалентни трансформации за опростяване на веригата. | |||
| 12360. | Техническа експлоатация на авиационни двигатели до прости устройства | 557,43 KB | |
| Техническата експлоатация на авиационната техника по своята същност е неразделна част от едно по-широко понятие - експлоатация. Тя включва такива компоненти като подготовка на самолети за полети, тяхната поддръжка, ремонт, съхранение и транспортиране. | |||
| 12205. | Разработване на методология за вземане на педагогически решения на базата на агрегиране на размити експертни оценки | 48,73 KB | |
| Много важна област за прилагане на принципите на TNM в смисъл на проектиране и вземане на ефективни педагогически решения е образователният процес в образователните институции, който се характеризира с доминиране на информация от субективен, езиков характер, което най-общо се обяснява с отношението на педагогическите системи към категорията на хуманистичните. | |||
Съвременната символна логика изгражда специални логически системи за анализ на дедуктивните разсъждения; един от тях се нарича логика на твърдениятаили пропозиционална логика,друг - предикатна логика.Нека разгледаме накратко принципите на конструиране на пропозиционалната логика.
Пропозиционалната логика е логическа система, която анализира процесите на разсъждение, разчитайки на характеристиките на истината на логическите връзки и абстрахирайки се от вътрешната структура на съжденията.
Езикът на пропозиционалната логика включва: азбука, дефиниране на правилно изградени изрази, тълкуване.
АзбукаПропозиционалната логика се състои от следните символи.
1) Символи за твърдения: p, q, r ... (пропозиционални променливи).
2) Символи за логически връзки:
Ù - връзка (съюз "и");
v - дизюнкция (съюз "или");
® - импликация (съюз „ако..., тогава...“);
º - еквивалентност (съюз "ако и само ако..., тогава..."); 1ù ù - отрицание („не е вярно, че...“).
3) Технически знаци (,) - скоби.
Изрази, допустими в пропозиционалната логика, наречени добре оформени формули или съкратени PPF, се въвеждат чрез следната дефиниция:
1. Всяка пропозиционална променлива - p, q, r ... - е PPF.
2. Ако A и B са PPF (A и B са символи на метаезик за всякакви формули), тогава изразите A Ù B, A v B, A ® B, A ºB, ùA също са PPF.
3. Всички други изрази, в допълнение към тези, предвидени в параграфи 1 и 2, не са PPF на езика на пропозиционалната логика.
Пропозиционалната логика може да бъде конструирана с помощта на табличен метод или като смятане, т.е. като система, която ви позволява да получавате, според правилата за извод, от едни формули към други.
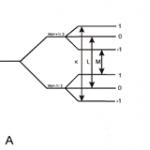
Таблична конструкцияприема семантични дефиниции на пропозиционални съединители под формата на матрици, показващи зависимостта на истинското значение на сложни формули от стойностите на съставните им прости формули. Ако A и B са прости формули, тогава истинското значение на формулите, конструирани с помощта на логически връзки, може да се представи по матричен начин - под формата на таблица (виж фиг. 36).
Сред правилно изградените формули, в зависимост от тяхната стойност на истината, те се различават еднакво вярно, еднакво невярноИ изпълними формули.
Идентично вярносе наричат формули, които приемат стойността на истината за всякакви - истински или неверни - стойности на съставните им пропозиционални променливи. Такива формули представляват законите на логиката.
Идентично невярносе наричат формули, които приемат стойността на фалшивост за всякакви - истински или невярни - стойности на пропозиционални променливи
Завършеноса формули, които могат да приемат стойности на истинност или фалшивост в зависимост от наборите от стойности на съставните им пропозиционални променливи.
Табличната конструкция включва дефиниране на логически връзки между формулите. От съществено значение за анализа на разсъждението е отношението на логическата импликация (символ |- ), което се определя по следния начин. от а 1, ..., Анкакто логически следват предпоставките INкато заключение, ако ако всеки Ai, ..., A n е верен, тогава също INВ обектния език отношението на следствието се изразява адекватно чрез подразбиране. Така че, ако a 1 , ..., A n |-B, след това формула, представляваща импликация на формата (A 1 Ù A 2 Ù ... Ù A n) ® B, трябва да е идентично вярно.
Табличната конструкция на пропозиционалната логика ви позволява да определите логическите връзки между твърденията (вижте глава V § 4) и да проверите правилността на заключенията, като използвате горния критерий. Като пример предлагаме да се извърши табличен метод за проверка на правилността на разсъжденията на формулата (р ®q) \- (ùq®ù r). Като заменим знака за логическо следствие между предпоставката и заключението с импликация и построим таблица за получената формула, виждаме, че тя е идентично вярна. Това означава, че разсъждението е правилно.
Ако аргументът съдържа повече от три променливи, тогава е трудно да се изгради пълна таблица, за да се провери нейната коректност, и тогава те използват съкратен метод за проверка, аргументирайки се от противоречие. Тъй като, с правилно разсъждение, формула на формата (A 1 Ù .. Ù A n) ® Bтрябва да бъде идентично вярно, нека да видим дали може да се окаже невярно за някакъв набор от стойности на променливи. Да кажем, че може. Ако получим някакво противоречие от това предположение, тогава такова предположение ще бъде неправилно и разсъждението, което се тества, ще бъде правилно. Ако не получим противоречие от предположението, тогава ще намерим набор от променливи стойности, за които формулата е невярна, т.е. наборът, който опровергава проверяваното разсъждение
Пропозиционалната логика като смятане- това е преди всичко т.нар система за естествено излюпване(СТАРТ).Апаратът в него са правилата за извод, всяко от които е някаква елементарна форма на извод. Придвижвайки се според тези правила от предпоставки или някои предположения към нови формули, те постепенно достигат до заключението. Заключението от помещенията се извършва, ако е било възможно да се премахнат всички направени предположения. По този начин под извеждане на формулата IN (заключения) от формули A 1 ,..., An (предпоставки) имаме предвид поредица от формули, всяка от които е или предпоставка, или предположение, или е получена съгласно правилата за извод от предходните, а последната формула от тази последователност е формула B и всички предположения са елиминирани.
Правилата на START ви позволяват да работите с всички връзки, налични в азбуката на езика. Те се делят на правила за въвеждане (в)И правила за изключваневързопи.
Съчетание:
| Дизюнкция: |
Ùв А, Б; Ù и 1 AÙB; Ù и 2 AÙB
A B AvB,ùA AvB,ù B
v в -- ; v в -- ; v и ----; v и
AvB AvB B A
Извод:
А® и A®B,ùB
Ú B B®A ùA
Отрицание:
ù и ù ù А
Еквивалентност:
º и АºВ
(A® B) Ù (B® A)
В допълнение към тези преки правила за получаване на нови редове на продукцията, в СТАРТприемат се косвени правила, които определят стратегията за конструиране на заключението. Например, ако трябва да извлечете от предпоставките формула на импликацията на формата (x 1 ® (x 2 ®...(x n - 1 ® x n))), то след изписване на предпоставките, всички антецеденти на заключението се изписват като предположения, започвайки с антецедента на главния знак на импликацията, т.е. x 1, x 2, x 3,..., x n - 1
G,A->B
Ако в същото време е възможно да се извлече x n, тогава според косвеното правило ® in ------ събиране
G®A®V
последователно формулите: (x n - 1 ® x n) (в този случай допускането x n -1 е изключено), (x n -2 ® (x n -1 ® x n) (x n -r е изключено от броя на допусканията) и т.н. ., докато получим търсеното заключение x 1 ®(x n -2 ®... (x n -1 ® x n). Това е правилото за конструиране на директно заключение.
Ето пример за изход с помощта на това правило:
((pÙq)®r) |-_ (p® (q ®r)
1. (р Ù q) ® r - предпоставка
2. p - предположение
3. q - предположение
4. r Ù q (2, 3. Ù in)
5. r (1,4, ® n)
6.q®r(3.5,®в)(-3)
7.p®(q®r)(2,6,®в)(-2)
Друго непряко правило се използва за конструиране на непряко заключение, в което предположението е отрицанието на B или отрицанието на последното следствие x n Г,А®(ВÙùВ)
Това правило има формата -------- и казва, че ако от
G-> |A
Някои формули (D) и предположения (A) водят до противоречие (B Ù ù B), тогава от тези формули следва ]A. Така, ако се конструира непряко извеждане на формула от вида (x 1 ® (x 2 ® ...(x n -1 -> x n)), тогава след предпоставките формулите се записват:
| X 2 |
предположения
ù x n предположение за косвени доказателства [DKD]
След това, съгласно правилата за извод, получаваме следствия от всички съществуващи предпоставки и предпоставки, докато не получим две противоречиви формули "(B и 1c), което показва несъвместимостта на предположението за косвени доказателства с други предположения и предпоставки. Оттук се прави заключение за неговата фалшивост ". Тогава редът 1]x p се включва в заключението и по този начин се изключва предположението за косвено доказателство. Например, нека извършим косвеното заключение: (p ® q) ½- (ù q ®ù p)
1 . p ® q- пакет
2. ù q- предположение
3. ù ù r dkd
4.p(3,] u)
5. q (1,4,® и)
6.q Ù q(5,2, Ù in)
7. ù ù ù p (6.3, ù in)(-3)
8. ù p (7, ù и)
9. ù q ® ù p (2,8, ® и)(-2)
Косвеният извод се счита за завършен, ако по време на извода се получи определена формула и нейното отрицание, т.е. противоречие. Така, ако се конструира косвено извеждане на формула на формата x 1 ® (x 2 ®... ® x n), след това запишете ред по ред всички предшественици от x 1 до X n -1като предположения; в последния ред напишете отрицанието на последното следствие - ] x nкато предположение за косвено заключение. Съгласно правилата за извод, ние получаваме различни следствия от всички съществуващи предпоставки и предположения. Получаването на две противоречиви следствия показва неистинността на предположението за косвено заключение. На тази основа DKDе отказано, т.е. получаваме двойно отрицание. Премахването на двойното отрицание дава формулата x n.
Основните логически свойства на естествената система за извод са нейните последователностИ завършеност.
Последователностозначава, че само верни следствия могат да бъдат получени от истински предпоставки и ако една формула е изводима от празен набор от предпоставки, тогава тя е идентично вярна. Това изключва възможността за извеждане на каквато и да е формула от празния набор от помещения ( А) и неговото отрицание ( ù А).
Завършеност на систематаозначава, че неговите дедуктивни средства са достатъчни, за да извлекат от празен набор от предпоставки всяка еднакво вярна формула.
Предикатната логика е по-обща логическа система и включва пропозиционалната логика като част от нея.Тя разполага с по-ефективни логически инструменти за анализ на разсъжденията на естествен език.
КОНТРОЛНИ ВЪПРОСИ
1. На какви видове изводи от сложни съждения се делят?
2. Как се изграждат чисто условните изводи?
3. Какво е условно категорично заключение? Назовете правилните му режими, изразете ги със символна нотация.
4. Какво заключение се нарича разделително-категорично? Назовете режимите му, изразете ги със символна нотация.
5. Посочете условията за правилността на изводите според утвърдително-отрицателния и отрицателно-утвърдителния начин на разделително-категорично заключение.
6. Какво заключение се нарича условно разделително (леммантично)? Какви режими има дилемата?
7. Какво е ентимема?
8. Какви са принципите на конструиране на пропозиционалната логика?
9. Покажете значението на различните видове условни и разделителни изводи в работата на адвоката.