Изчислете дължината на дъгата на циклоида онлайн. Циклоид

Изпратете добрата си работа в базата знания е лесно. Използвайте формата по-долу

Студенти, докторанти, млади учени, които използват базата от знания в обучението и работата си, ще ви бъдат много благодарни.

публикувано на http://www.allbest.ru/

Образователна институция

„Беларуски държавен педагогически

Университет "Максим Танк"

Физико-математически факултет

Катедра по математика и методика на обучението по математика

КУРСОВА РАБОТА ПО ТЕМАТА

"ЦИКЛОИД"

Минск, 2016 г

циклоидна дъга тавтохронно махало

Въведение
1. Основни свойства на циклоида
2. Геометрична дефиниция на циклоида
3. Област на циклоидната арка
4. Дължина на дъгата на циклоидната дъга
5. Обем на тяло, получено чрез завъртане на дъгата на циклоида
6. Най-доброто махало
Заключение
Библиография

ВЪВЕДЕНИЕ

Темата на курсовата ми работа е циклоида. Тази крива е забележителна по много начини. Това е и следа от точка върху ръба на търкалящо се колело, също е крива на колебания с постоянен период, също е крива на най-бързото спускане. В наши дни циклоидалните криви се използват в много технически изчисления и познаването на тези криви улеснява изучаването на машинни части. Без да навлизаме в подробности, ще споменем, че свойствата на циклоидалните криви се използват при конструиране на профили на зъбни колела и в много други технически въпроси. Дори от чисто приложна гледна точка тези криви заслужават най-сериозно внимание. Затова сметнах тази тема за актуална и интересна за изучаване.

Какви проблеми възникват при изучаването на циклоида? Първо, трябва да му дадем чисто геометрична дефиниция, независима от механиката. След това трябва да проучите неговите свойства, да вземете предвид тангентата, да изчислите площта, ограничена от циклоидната арка и нейната основа, дължината на дъгата, обема на тялото, образувано от въртенето на циклоидната арка около насочващата линия.

Курсовата работа ще разгледа подробно тавтохронното свойство на циклоида и използването му за създаване на най-доброто махало. Значението на часовниците с махало не може да се подценява, тъй като доскоро те служеха като най-точните часовници, осигуряващи обслужване на времето в астрономическите обсерватории.

Друго достойнство на циклоида, което не може да бъде пренебрегнато, е, че е използвано от учените при разработването на техники за изследване на криви линии, което доведе до изобретяването на диференциално и интегрално смятане. В моята работа предлагам да сравня изчисляването на дължината на дъгата на циклоидната арка, повърхността под арката и обемите на телата, образувани от въртенето на циклоидната арка преди появата на интегралното смятане, дълго и не винаги абсолютно стриктно и използвайки интеграция.

Цел на работата:учебен материал по темата „Циклоид”; изучаване на характеристиките на най-доброто махало; сравнение на изследването на криви линии преди и след появата на интегралното смятане, изчисляване на дължината на дъгата на циклоидната дъга, повърхността под арката и обемите на телата, образувани от въртенето на циклоидната арка.

1. ОСНОВНИ СВОЙСТВА НА ЦИКЛОИДА

Първо трябва да разберете коя крива се нарича циклоида.

Помислете за кръг с радиус ас център в точка А. Оставете въпросния кръг да се търкаля, без да се хлъзга по оста OX. Кривата, описана от всяка точка на окръжността, се нарича циклоид.

Тази дефиниция на циклоидата никога не е удовлетворявала учените: в края на краищата тя се основава на механични понятия - скорост, добавяне на движения и т.н. Следователно геометрите винаги са се стремили да дадат на циклоидата "чисто геометрична дефиниция". Но за да дадат такова определение, е необходимо преди всичко да се изучат основните свойства на циклоида, като се използва неговата механична дефиниция. След като изберем най-простото и най-характерното от тези свойства, можем да го използваме като основа за геометрична дефиниция.

Нека започнем с изучаването на допирателната и нормалата към циклоидата. Какво стана допирателнадо крива линия, всеки си представя съвсем ясно; затова няма да го представяме тук. нормалносе нарича перпендикуляр на допирателната, възстановен в точката на контакт. На фиг. 1.1 показва допирателната и нормалата към кривата AB в нейната точка M.

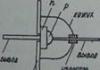
Нека разгледаме циклоида (фиг. 1.2). Кръг се търкаля по права линия AB. Да приемем, че вертикалният радиус на окръжността, който в началния момент е преминал през долната точка на циклоидата, е успял да се завърти под ъгъл μ и е заел позиция OM. С други думи, ние вярваме, че сегментът M o T съставлява такава част от сегмента M o M 1, каквато ъгълът q образува от пълен оборот. В този случай точка М 0 стигна до точка М.

Точка M е точката на циклоидата, която ни интересува.

Стрелка ОХизобразява скоростта на движение на центъра на въртяща се окръжност. Всички точки от окръжността, включително точка М, имат еднаква хоризонтална скорост, но освен това точка М участва във въртенето на окръжността. Скоростта MC, която точка M от окръжността получава при това въртене, е насочена по допирателната Г-ЦА 1 към окръжността, т.е. перпендикулярно на радиуса ОМ.И защото в този случай скоростта на MS е равна по големина на скоростта на MP (т.е. скоростта ТОЙ).Следователно успоредникът на скоростите в случая на нашето движение ще бъде ромб (ромбът MSKR на фиг. 1.2). Диагоналът MK на този ромб ще ни даде допирателната към циклоидата.

Всичко по-горе дава възможност да се реши следната конструктивна задача: дадена е насочващата линия AB на циклоидата, радиусът r на образуващата окръжност и точката M, принадлежаща на циклоидата (фиг. 1.2). Необходимо е да се построи допирателна към МС към циклоидата.

Имайки точка M, можем лесно да конструираме генерираща окръжност в нейната позиция, когато точка от окръжността попада в M. За да направим това, първо намираме центъра ОТНОСНОизползвайки радиус МО= r (точка O трябва да лежи на права линия, успоредна на AB, на разстояние r от нея). След това построяваме отсечка MP с произволна дължина, успоредна на насочващата права. След това изграждаме права линия Г-ЦА 1 , перпендикулярно на ОМ. На тази права линия отстъпваме от точката Мсегмент MC равен на MP. На MC и MP, както отстрани, изграждаме ромб. Диагоналът на този ромб ще бъде допирателна към циклоидата в точка M.

Тази конструкция е чисто геометрична, въпреки че я получихме с помощта на концепциите на механиката. Сега можем да кажем сбогом на механиката и да получим по-нататъшни последствия без нейната помощ. Нека започнем с една проста теорема.

Теорема 1. Ъгъл между допирателната към циклоида (в произволна точка)и насочващата линия е равна на допълнението на 90°половината от ъгъла на завъртане на радиуса на производствения кръг.

С други думи, на фиг. 1.2

? KLTравно на или

Сега ще докажем това равенство. За да съкратим речта, ще се съгласим да наречем ъгъла μ на въртене на радиуса на генериращата окръжност „главен ъгъл“. Това означава, че ъгълът MOT на фиг. 1.2 -- основен ъгъл. Главният ъгъл ще считаме за остър. За случая, когато кръгът на търкаляне прави повече от една четвърт от пълен оборот, доказателството ще бъде подобно.

Нека разгледаме ъгъла SMR. Страната CM е перпендикулярна ОМ(допирателната към окръжността е перпендикулярна на радиуса). Страната MP (хоризонтална) е перпендикулярна на ОТ(към вертикала). Но ъгъл MOP по конвенция е остър, а ъгъл CMR е тъп. Така че ъглите МОТИ СМРсбор до 180° (ъгли с взаимно перпендикулярни страни, едната от които е остра, а другата тъпа).

И така, ъгъл CMP е 180° -ts. Но, както знаете, диагоналът на ромба разделя ъгъла на върха наполовина. Следователно,

KMR = 90° -,

Q.E.D.

Нека сега насочим вниманието си към нормалата към циклоидата. Нека изобразим лявата страна на фиг. 1.2 е по-голямо и нека начертаем нормално M.E. (M.E. ? МК; ориз. 1.3).

От фиг. 1.3 следва, че ъгълът EMP е равен на разликата между ъглите KMEИ KMR, т.е. равен на 90° - ? KMP.

Но току-що доказахме, че самият ъгъл KMRравен на 90° -

Така получаваме:

? RME= 90° - ? KMR= 90° - (90° -) =

Доказахме проста, но полезна теорема. Нека дадем формулировката му:

Теорема 2.Ъгъл между нормалата към циклоидата (по всяко време)а насочващата линия е равна на половината от „основния ъгъл“.

Нека сега свържем точката (T) на образуващата окръжност с точката M („текущата“ точка на циклоидата) с долната (с точката на допиране на генериращата окръжност и насочващата линия - Фиг. 1.3) . Триъгълникът MOT очевидно е равнобедрен (OM и ОТ-- радиуси на генериращата окръжност). Сборът от ъглите при основата на този триъгълник е равен на 180° - μ, а всеки от ъглите при основата е половината от тази сума. Така, ? OMT= 90° - .

Нека обърнем внимание на ъгъла RMT.Тя е равна на разликата в ъглите OMTИ OMR. Сега видяхме това ? OMTравен на 90° - ; Що се отнася до ъгъла OMR, не е трудно да разберете на какво е равен. В крайна сметка ъгълът OMRравен на ъгъл DOM(вътрешни кръстосани ъгли, когато са успоредни).

Веднага се вижда, че ? DOM равен на 90° - c. Означава, ? OMP= = 90° - c. Така получаваме:

RMT = ? OMT - ? OMR = 90° - - (90° - c) = .

Резултатът е забележителен: ъгъл RMTсе оказва равен на ъгъла PME (по теорема 2). Следователно директно МЕН и МТ ще се слеят! Нашият ориз. 1.3 не е направено съвсем както трябва! Правилното разположение на линиите е показано на фиг. 1.4.

Нека формулираме получения резултат под формата на теорема 3.

Теорема 3 (първото основно свойство на циклоида).Нормалата към циклоидата минава през „долната“ точка на генериращата окръжност.

Тази теорема има просто следствие. Ъгълът между допирателната и нормалата по дефиниция е прав ъгъл. Това е ъгълът, вписан в обиколката на образуващата окръжност. Следователно тя трябва да лежи върху диаметъра на кръга. Така, TT 1 -- диаметър и T 1 -- “горна” точка на генериращата окръжност. Нека формулираме получения резултат.

Следствие (второ основно свойство на циклоидата).Допирателната към циклоидата минава през „горната“ точка на генериращата окръжност.

За да обясним това свойство, трябва да построим циклоида.

Циклоидата се изгражда в следната последователност:

1. Върху хоризонталната водеща линия е положена отсечка AA 12, равна на дължината на образуващата окръжност с радиус r, (2рr);

2. Построете образуваща окръжност с радиус r, така че насочващата права да се допира към нея в точка А;

3. Окръжността и отсечката AA 12 се разделят на няколко равни части, например 12;

4. От разделителните точки 1 1, 2 1, ...12 1 се възстановяват перпендикуляри до пресичането им с продължението на хоризонталната ос на окръжността в точки 0 1, 0 2, ...0 12;

5. От разделителните точки на окръжността 1, 2, ...12 се изчертават хоризонтални линии, върху които се правят резки с дъги на окръжност с радиус r;

6. Получените точки A 1, A 2, ...A 12 принадлежат на циклоидата.

На фиг. 1.6 основата на циклоидата е разделена на 6 равни части;

Колкото по-голям е броят на деленията, толкова по-точен ще бъде чертежът. Във всяка точка от циклоидата, която сме построили, начертаваме допирателна, свързваща точката на кривата с “горната” точка на образуващата окръжност. В нашия чертеж имаме седем допирателни (две от тях са вертикални). Сега, рисувайки циклоидата на ръка, ще се погрижим тя действително да докосне всяка от тези допирателни: това значително ще увеличи точността на чертежа. В този случай самата циклоида ще се огъва около всички тези допирателни).

Нека начертаем същата фигура. 1.6 нормали във всички открити точки на циклоидата. Ще има общо пет нормални, без да се брои ръководството. Можете да изградите обвивката на тези нормали на ръка. Ако бяхме взели 12 или 16 разделителни точки вместо шест, тогава щеше да има повече нормали в чертежа и обвивката щеше да бъде очертана по-ясно. Тази обвивка на всички нормали играе важна роля при изучаването на свойствата на всяка крива линия. В случай на циклоида се разкрива интересен факт: обвивката на нормалите на циклоидата е точно същата циклоида, само изместена с 2 анадолу и нататък ранадясно. Този факт е характерен специално за циклоида.

2. ГЕОМЕТРИЧНА ОПРЕДЕЛЕНИЕ НА ЦИКЛОИД

Сега ще дадем дефиниция на циклоида като геометрично място на точки, без да използваме механика. Най-лесният начин е да го направите по този начин. Помислете за произволна права линия AB(посоката му условно ще считаме за хоризонтална) и точка върху него М 0 . След това разглеждаме всички възможни кръгове с определен радиус, докосващи тази права линия и разположени от едната й страна. На всеки кръг от точката Tдокосвайки го с права линия ABостави настрана (към точката М 0 ) дъга TM,равна по дължина на сегмента М 0 T.Геометрично място на точките М(взети на всички кръгове, които споменахме) и ще бъде циклоида.

Нека установим друго важно свойство на циклоидата и се опитаме да го използваме като основа за изучаване на тази крива.

Помислете за триъгълник MTT 1 (фиг. 2.1), образувана от вертикалния диаметър на образуващата окръжност, допирателната към циклоидата и нормалата към нея.

Ъгъл MT 1 T, както е вписан в кръг, е равен на половината от централния ъгъл, основан на същата дъга, т.е. равен. Нека изпълним MK||AV И M.E.?AB.Сегментът ME ще играе важна роля в бъдеще, така че ще му дадем име и обозначение: ще го наречем „височината“ на точката M на циклоидата и ще го обозначим с буквата ч.Така че височината на точката Мциклоидите са неговото разстояние от насочващата линия.

Нека обърнем внимание на ъгъла KMT. То е равно на ъгъла MT 1 T. От триъгълник TMT 1 получаваме:

MT = 2 Агряхи от триъгълника TCM:

CT = MT sin.

Сравнявайки тези резултати и отбелязвайки, че CT = h, най-накрая получаваме:

ч = 2 агрях 2.

Изразихме височината на точка M чрез ъгъла между допирателната в точка M и вертикалата (все още считаме посоката на правата AB за хоризонтална). Сега нека изразим синуса на този ъгъл чрез „височината“. Очевидно получаваме:

къде през кпоказва постоянна стойност за дадена циклоида . Представяме получения резултат в теорема.

Теорема 4.Синусът на ъгъла между допирателната към циклоидата в точка М и вертикалата е пропорционален на корен квадратен от „височината“ на точка М.

Очевидно всяка циклоида има това свойство. Възниква въпросът: до каква степен това свойство характеризира циклоидата: дали всяка крива, притежаваща това свойство, непременно ще бъде циклоида? Може да се докаже, че това ще бъде точно така - че следната (обратна) теорема също е вярна:

Теорема 5.Ако са дадени права AB и точка M, тогава единствената крива, която отговаря на условията на теорема 4 и минава през точката M, е циклоида.

В този случай радиусът на генериращата окръжност на тази циклоида е свързан с коефициента к, което е споменато в теорема 4, чрез следната връзка:.

Струва си да се обърне внимание и на друга забележителна крива, наречена спътник на циклоида.

Нека разгледаме циклоида (фиг. 2.2). От нейната точка М спускаме перпендикуляр към вертикалния диаметър на образуващата окръжност. Получаваме точка P. Нека извършим тази конструкция за всички точки на циклоидата без изключение.

Тогава точка P ще опише някаква крива. Тази крива се нарича спътник на циклоидата

Да разгледаме циклоида, точка M върху нея и съответната точка P върху нейния спътник (фиг. 2.3) Нека означим центъра на образуващата окръжност с буквата Q. Тогава ще имаме:

QP=QM cos?MQP= а cos(180 0 -ts)=- а cosс=- а sin(90 0 -ts)= а sin(t -90 0).

Нека начертаем геометричното място на центровете на генериращата окръжност (правата линия XX 1 ). От точка М 0 нека отложим до ABлинейна отсечка М 0 К, равен. Нека изпълним KY ? XX 1 . Нека означим пресечната точка на тези линии с буквата ОТНОСНО. Линеен сегмент М 0 Рна насочващата права линия от върха на циклоидата до точката на контакт на генериращата окръжност е равно на а q, където q е главният ъгъл MQР, изразено в радиани. Линеен сегмент OQпо хоризонталната ос XX 1 равно на М 0 Р - М 0 К=а(ts -) и сегмента QPравно на агрях? PMQ, т.е. равен на синуса на ъгъла (t -), умножен по радиуса а.

И така, от точката ОТНОСНОСегменти, равни по дължина на дъгите на окръжност, са разположени хоризонтално, а линиите на синусите на ъглите, съответстващи на тези дъги, са разположени вертикално. Това е познатата конструкция на обикновена синусоида.

означава, Спътникът на циклоида се нарича синусоида.

Няма да се задълбочаваме в изследването на свойствата на тази наистина забележителна крива, а само ще отбележим като факт, че площта, ограничена от спътника на една арка на циклоида и нейната основа, е равна на удвоената площ на генериращия кръг.

3. АРКА АРКА НА ЦИКЛОИДАТА

Първото споменаване на изчисляването на площта, затворена между арката на циклоида и нейната основа, е в трудовете на Вивиани и Торичели. При това те използваха специална техника, наречена „метод на неделимите“. Този метод се състои в разделяне на криволинейна фигура на безкрайно тънки ленти, чиято площ е относително лесна за намиране, след което тези области се сумират. Тази техника доведе до появата на интегралното смятане половин век по-късно.

Помислете за фигура, ограничена от циклоидна дъга и синусоида. На фигура 3.1 тази фигура, състояща се от две венчелистчета, е очертана с дебела линия. Нека започнем да изчисляваме неговата площ.

Първо, нека изградим огледален образ на дясното венчелистче на фигурата спрямо насочващата права линия AB (това отражение е дадено на фигура 4.1 с пунктирана линия). Нека след това преместим тази пунктирана крива нагоре наляво и да я приложим към лявото венчелистче, така че дъгите на синусоидите, включени в контура на всяко от венчелистчетата, да съвпадат. Получаваме изпъкнала фигура, защрихована на фигура 3.1 и показана отделно на фиг. 3.2. Тази фигура се нарича фигурата на Робервал. Нека установим най-важните свойства на тази фигура.

1. Изпъкналата фигура M 0 PLM е равна по размер на двулопастната фигура, изобразена с дебелата линия на фиг. 3.1. Това личи от факта, че е „съставен“ от едни и същи венчелистчета.

2. Всяка хоризонтална хорда на изпъкнала фигура е равна на удвоената хорда на венчелистчето, разположено на същото разстояние от AB. Наистина, хордите CE и RN (фиг. 3.1) на дясното венчелистче, равноотдалечени от образуващата окръжност, са еднакво отдалечени от центъра. Това означава CT = CE = RN = P 1 N 1 = TL.

Това дава важен резултат: хордата MR на изпъкнала фигура (фиг. 3.2) е равна на хордата на образуващата окръжност SC, разположена на същото разстояние от насочващата линия.

Нека сега разгледаме изпъкналата фигура на Робервал и окръжността, докосващи едни и същи прави линии AB и A 1 B 1, и да свържем точките на тяхното пресичане с окръжността и с контура на изпъкналата фигура последователно с прави сегменти, както е показано на фигурата. Ще наричаме получените по този начин вписани многоъгълници (HLMNPQRSTK и H 1 L 1 M 1 N 1 P 1 Q 1 R 1 S 1 T 1 K 1) „съответстващи“ многоъгълници на поредица от трапеци (и триъгълници). Площите на „съответстващите“ трапеци в кръг и във фигура на Робъруел, например NPRS и N 1 P 1 R 1 S 1, са равни, тъй като тези трапеци имат съответно равни долни основи, горни основи (съответни хорди) и височини. На фиг. 3.2 съответни трапеца с еднакъв размер са покрити с идентично засенчване.

Сега ще увеличим за неопределено време броя на „междинните“ линии, успоредни на AB, така че разстоянието между всяка съседна двойка да клони към нула. Тогава в кръг получаваме поредица от вписани многоъгълници, чийто брой на страните нараства неограничено и всяка от страните клони към нула. Знаем, че площите S n на тези многоъгълници имат границата на площта на кръга:

лим С н=стр а 2 .

Как ще се държи последователността от многоъгълници, вписани в изпъкнала фигура на Робервал в този случай? Квадрат? n последователни вписани многоъгълници ще се стремят към областта? Фигури на Робервал. Известно е, че ако две променливи величини запазват съответно еднакви стойности за всичките си промени и едната от тях клони към определена граница, то другата клони към същата граница. Но всеки многоъгълник, вписан във фигура на Робервал, е равен по размер на съответния многоъгълник, вписан в кръг. Следователно заключаваме, че границата на площите на многоъгълници, вписани във фигура на Робервал, е равна на границата на площите на съответните многоъгълници, вписани в кръг; което означава, че площта на изпъкналата фигура на Робервал е равна на площта на генериращия кръг:

От тук получаваме незабавно следствие: площта на фигурата с две венчелистчета е равна на площта на генериращия кръг.

Нека сега погледнем Фигура 3.1. Площта на фигурата AOTPBKA, както видяхме, е равна на удвоената площ на генериращия кръг. Току-що определихме площта на фигурата с две венчелистчета: тя е равна на площта на генериращия кръг. следователно площта, ограничена от арката на циклоида и нейната основа, е равна на утроената площ на генериращия кръг.

Сега нека намерим областта, затворена между дъгата на циклоидата и нейната основа, използвайки диференциална геометрия.

Където T? .

Нека намерим производната

4. ДЪГА НА ЦИКЛОИДНАТА ДЪГА

Дължината на дъгата на циклоида е изчислена за първи път от английския архитект и математик Рен през 1658 г. Рен изхожда от механични съображения, напомнящи първите произведения на Торичели и Робервал. Той разгледа въртенето на търкалящ се кръг под много малък ъгъл близо до „долната“ точка на генериращия кръг. За да се даде демонстративна сила на внушителните съображения на Рен, би било необходимо да се разгледа цяла поредица от спомагателни теореми и съответно би било необходимо да се изразходва твърде много работа.

Много по-удобно е да използвате по-дълъг, но лек път. За да направите това, трябва да вземете предвид специалната крива, която има всяка плоска крива - нейното развитие.

Да разгледаме изпъкнала дъга AB на крива линия (фиг. 4.1). Нека си представим, че гъвкава, неразтеглива нишка със същата дължина като самата дъга AB е прикрепена към дъгата AB в точка A и тази нишка е „увита“ върху кривата и прилепва плътно към нея, така че краят й съвпада с точката B. Ще „разгънем“ -- изправим конеца, като го държим опънат, така че свободната част на конеца CM да бъде винаги насочена тангенциално към дъгата AB. При тези условия краят на нишката ще опише определена крива. Тази крива се нарича развитие или на латински еволвентеноригинална крива.

Ако дъгата на кривата не е изпъкнала навсякъде в една посока, ако е като кривата AB на фиг. 4.2, има точка C, в която допирателната към кривата преминава от едната страна към другата (такава точка се нарича инфлексна точка), тогава в този случай можем да говорим за развитие на кривата, но разсъжденията ще имат да е малко по-сложно.

Нека си представим, че нишката е фиксирана точно в точката на инфлексия C (фиг. 4.2). Нишката, развиваща се от дъгата BC, ще опише BMR кривата - сканирането.

Сега нека си представим нишка, навита около дъга AC на оригиналната крива, но тази нишка вече е удължена: в точка C към нея е завързано парче нишка CP. Чрез навиване на удължената ACP нишка с кривата CA получаваме РНК дъга, която заедно с BMP дъгата образува една непрекъсната крива - непрекъсната, но не гладка навсякъде: точката на отклонение C на оригиналната крива ще съответства на върха (точка на връщане) на кривата на BMRNA: кривата на BMRNA ще бъде еволвента (размах) на кривата BCA.

Тези примери ни помогнаха да свикнем с новите концепции за еволюта и еволвента. Сега нека проучим развитието на циклоидалните криви.

Когато изучаваме тази или онази крива, често изграждаме спомагателна крива - „придружител“ на тази крива. И така, струваме синусоида - спътник на циклоида. Сега, въз основа на тази циклоида, ще построим спомагателна циклоида, неразривно свързана с нея. Оказва се, че съвместното изследване на такава двойка циклоиди е в някои отношения по-просто от изследването на един отделен циклоид. Ще наричаме такава спомагателна циклоида придружаваща циклоида.

Нека разгледаме половината от арката на циклоидата AMB (фиг. 4.3). Не трябва да се смущаваме, че тази циклоида е разположена по необичаен начин („с главата надолу“). Нека начертаем 4 прави линии, успоредни на водещата права линия AK на разстояния а, 2а, 3аи 4 а. Нека построим генерираща окръжност в позицията, съответстваща на точка M (на фиг. 4.3 центърът на тази окръжност е обозначен с буквата O). Нека означим ъгъла на завъртане MON с c. Тогава отсечката AN ще бъде равна на bc (ъгълът c се изразява в радиани).

Продължаваме диаметъра NT на образуващата окръжност отвъд точка T до пресечната точка (в точка E) с права линия PP. Използвайки TE като диаметър, ще построим кръг (с център O 1). Нека построим допирателна в точка M към циклоидата AMB. За да направите това, както знаем, точка M трябва да бъде свързана с точка T. Нека удължим допирателната MT през точка T, докато се пресече със спомагателната окръжност и наричаме пресечната точка M 1. Това е тази точка M 1, с която сега искаме да се справим.

Означихме ъгъла MON с c. Следователно ъгълът MTN ще бъде равен на (вписания ъгъл, базиран на същата дъга). Триъгълник TO 1 M 1 очевидно е равнобедрен. Следователно не само ъгълът O 1 TM 1, но и ъгълът TM 1 O 1 ще бъдат равни. Така частта от ъгъла TO 1 M 1 в триъгълника TO 1 M 1 остава точно p - q радиана (не забравяйте, че ъгълът 180? е равен на p радиана). Нека също да отбележим, че сегментът NK очевидно е равен на b(p - q).

Нека сега разгледаме кръг с център O 2, показан на фиг. 4.3 с пунктирана линия. От чертежа става ясно какъв кръг е това. Ако го търкаляте без плъзгане по права линия NE, тогава неговата точка B ще описва циклоидата BB. Когато пунктираната окръжност се завърти под ъгъл p - c, центърът O 2 ще дойде в точка O 1, а радиусът O 2 B ще заеме позиция O 1 M 1. Така построената от нас точка M 1 се оказва точка от циклоидата BB.

Описаната конструкция свързва всяка точка M от циклоидата AMB с точка M 1 от циклоидата VM 1 B. На фиг. 4.4 показва това съответствие по-ясно. Получената по този начин циклоида се нарича придружаваща. На фиг. 4.3 и 4.4, циклоидите, изобразени с дебели прекъснати линии, са съпътстващи по отношение на циклоидите, изобразени с дебели плътни линии.

От фиг. 4.3 е ясно, че правата MM 1 е нормална в точка M 1 към придружаващата я циклоида. Наистина, тази права минава през точка M 1 на циклоидата и през точката T на допиране на образуващата окръжност и насочващата линия („най-ниската“ точка на образуващата окръжност, както казахме веднъж; сега се оказа, че „най-високият“, защото чертежът е завъртян). Но същата права линия, по конструкция, е допирателна към „основата“ на циклоидата AMB. По този начин оригиналната циклоида се докосва до всяка нормала на придружаващата циклоида. Това е обвивката за нормалите на придружаващата циклоида, т.е. неговата еволюция. И „придружаващата“ циклоида се оказва просто еволвента на оригиналната циклоида!

Като се включихме в тази тромава, но по същество проста конструкция, ние доказахме една забележителна теорема, открита от холандския учен Хюйгенс. Това е теоремата: Еволютата на една циклоида е точно същата циклоида, само изместена.

След като изградихме еволюта не за една арка, а за цялата циклоида (което, разбира се, може да се направи само психически), след това еволюта за тази еволюта и т.н., получаваме Фиг. 4.5, наподобяващи плочки.

Нека обърнем внимание на факта, че при доказването на теоремата на Хюйгенс не използвахме нито безкрайно малки, нито неделими, нито приблизителни оценки. Ние дори не използвахме механика, въпреки че понякога използвахме изрази, заимствани от механиката. Това доказателство е напълно в духа на разсъжденията, използвани от учените от 17 век, когато те искат да обосноват стриктно получените резултати, използвайки различни водещи съображения.

Едно важно следствие непосредствено следва от теоремата на Хюйгенс. Разгледайте сегмента AB на фиг. 4.4. Дължината на този сегмент очевидно е 4 а. Нека сега си представим, че нишка е навита около дъгата AMB на циклоидата, фиксирана в точка A и оборудвана с молив в точка B. Ако „навием“ нишката, моливът ще се движи по протежение на циклоидата AMB , т.е. по циклоидата BM 1 B. Дължината на нишката, равна на дължината на полуарката на циклоидата, очевидно ще бъде равна на сегмента AB, т.е., както видяхме, 4 а. Следователно дължината L на цялата циклоидна арка ще бъде равна на 8 аи формулата L=8 асега може да се счита за доста строго доказано.

Нека изчислим дължината на дъгата с помощта на диференциална геометрия. Полученото по този начин решение ще бъде много по-кратко и по-лесно:

Където T?

r(t)=

| r(t)|===2 грях

5. ОБЕМ НА ТЯЛО, ПОЛУЧЕНО ЧРЕЗ ВЪРТЕНЕ НА АРКАТА НА ЦИКЛОИД

Нека намерим обема на тялото, генериран от въртенето на циклоидната дъга около нейната основа. Робервал го открива, като разбива полученото яйцевидно тяло (фиг. 5.1) на безкрайно тънки слоеве, вписвайки цилиндри в тези слоеве и сумирайки техните обеми. Доказателството се оказа дълго, досадно и не съвсем строго. Затова, за да го изчислим, се обръщаме към висшата математика. Нека дефинираме параметрично уравнението на циклоидата.

В интегралното смятане, когато се изучават обеми, се използва следната забележка:

Ако кривата, ограничаваща криволинейния трапец, е дадена с параметрични уравнения и функциите в тези уравнения отговарят на условията на теоремата за промяната на променливата в определен интеграл, тогава обемът на тялото на въртене на трапеца около оста Ox ще се изчислява по формулата:

Нека използваме тази формула, за да намерим обема, от който се нуждаем.

По същия начин изчисляваме повърхността на това тяло.

L=((x,y): x=a(t - sin t), y=a(1 - цена), 0 ? t ? 2р)

В интегралното смятане има следната формула за намиране на повърхността на въртящо се тяло около оста x на крива, дефинирана параметрично на сегмент (t 0 ?t ?t 1):

Прилагайки тази формула към нашето циклоидно уравнение, получаваме:

Нека разгледаме и друга повърхност, генерирана от въртенето на циклоидната дъга. За да направите това, ще изградим огледален образ на циклоидната арка спрямо нейната основа и ще завъртим овалната фигура, образувана от циклоида и нейното отражение около оста KT (фиг. 5.2)

Първо, нека намерим обема на тялото, образувано от въртенето на циклоидната дъга около оста KT. Ще изчислим неговия обем по формулата (*):

Така изчислихме обема на половината от това тяло с форма на ряпа. Тогава целият обем ще бъде равен

За да намерите повърхността на това тяло на въртене с помощта на интеграл, също е необходимо да го разделите наполовина хоризонтално и да разгледате горната му част.

Това означава, че повърхността на полученото тяло е равна на

6. НАЙ-ДОБРОТО МАХАЛО

Наблюдавайки люлеещ се полилей в храма, Галилей открива, че времето за пълното люлеене на полилея, т.е. време, след което ще се върне в първоначалното си положение (т.нар период на трептене), беше еднакъв както за големи, така и за малки диапазони. Това наблюдение доведе Галилей до идеята, че люлеещо се тяло (махало) може да се използва за регулиране на скоростта на часовника.

Самият Галилей не успява да въведе часовник с махало и скоро става ясно, че наблюденията му са неточни. По-точни наблюдения показват, че периодът на трептене на махалото е толкова по-дълъг, колкото по-голямо е люлеенето; но поради неизбежното триене на оста и съпротивлението на въздуха, диапазонът на трептене на обикновено махало непрекъснато намалява, което означава, че периодът на неговите трептения също ще намалее. Часовник с обикновено махало - иначе се нарича кръгово махало(тъй като всяка точка от него описва дъга от окръжност), те не могат да вървят правилно.

Хюйгенс разбра какъв вид адаптация трябва да се направи на кръгло махало, така че то да има постоянно люлеене. Но той реши и друга интересна задача - отговори на въпроса по коя крива трябва да се движи една точка, така че периодът на нейните трептения да не зависи от амплитудата. Той измисли дизайн, който накара центъра на тежестта на махалото да се движи по тази крива.

Да започнем с устройство, което осигурява правилното движение на часовник с кръгло махало. Gear А(фиг. 6.1), задвижван от верига с тежест INнакрая. На оста на това колело е монтирано зъбно колело, което е плътно свързано с него. Тази предавка задвижва стрелките на часовника и затова е необходимо колелото А движеха се равномерно.

Но теглото IN, като всяко тяло, ще се движи ускорено под въздействието на гравитацията, придавайки ускорено въртене на колелото А. Махалото трябва да елиминира трудността ММ.

котва СЪС, лежаща в равнината на колелото А, плътно свързан с махалото ММ, самото махало ММлежи извън равнината на чертежа и затова се чертае с пунктирана линия. Котвата е оборудвана със зъби нИ ДА СЕ.

В момента, показан на фиг. 6.1, колело Азадържан от левия зъб нкотви СЪС.Когато махалото се завърти наляво, зъбът нкотвата ще освободи уловеното зъбно колело на колелото и колелото ще се завърти, но само от зъбното колело, защото зъбното колело ДА СЕкотвата ще падне в пролуката между зъбите на колелото и ще го задържи. Когато след това махалото отново се завърти надясно, зъбът от тази страна ще бъде задържан от котвата. И така, при всяко пълно завъртане на махалото (напред и назад), колелото ще се върти точно с един зъб, т.е. до определена част от обиколката. Движението на колелото ще бъде строго равномерно. Зъбите на котвата, както се вижда от фиг. 6.1, се нарязват наклонено, така че зъбът на колелото, който е задържан от котвата и отново е освободен, трябва да се плъзга по наклонената повърхност на зъба на котвата. В резултат на това котвата ще даде на махалото малък тласък. Тези ритмични удари ще компенсират загубата на енергия, която махалото изразходва за преодоляване на триенето и съпротивлението на въздуха. Следователно люлеенето на махалото няма да намалее. По този начин тежестта предава енергия както на часовниковите колела, така и на самото махало; махалото регулира часовника.

Ами ако часовникът спре? Не е трудно да ги използвате: просто вдигнете тежестта и завъртете махалото. Но в този случай диапазонът на люлеене може да се окаже различен и часовникът ще се движи равномерно, но неправилно (ще върви напред или ще започне да изостава). Хюйгенс измисли устройство, което улеснява настройването на часовника. Но Хюйгенс, като истински учен, се интересуваше от въпроса: какво трябва да бъде „перфектното“ махало, махало, чието време на люлеене не зависи от люлеенето? Нека разгледаме подробно как Хюйгенс разреши този проблем.

Думата "тавтохрон" означава "униформен". Това е, което Хюйгенс нарича кривата, която започва да търси, т.е. такава крива, по която трябва да се движи центърът на тежестта на махалото, така че периодът на неговото люлеене да не зависи от големината на люлеенето. Търсенето беше увенчано с успех: мистериозният тавтохрон се оказа наскоро проучен циклоид. В същото време Хюйгенс проявява изключително остроумие. Достатъчно е да се каже, че учението за еволютите е създадено в процеса на решаване именно на този проблем.

Хюйгенс разсъждава по следния начин. Нека си представим жлеб във формата на циклоид, както е показано на фиг. 6.2.

По този жлеб се търкаля тежка топка М. Ще разгледаме идеалния случай - случаят, когато няма триене и въздушно съпротивление.

Нека обозначим точките на върха на циклоидата с М 0 и М? 0 , и радиусът на генериращата окръжност е през А. Нека начертаем окръжност с радиус А, допирателна към циклоидата във върха (окръжност с център ОТНОСНО) и генерираща окръжност в позиция, съответстваща на точката Мциклоиди (посочени с пунктирана линия). Да речем, че поставихме топката в точката М 1 жлеб и го пусна без натискане. Под въздействието на гравитацията тя ще се търкаля надолу. Нека проучим движението му.

Каква ще бъде скоростта на топката, когато достигне точката Мциклоиди? Не е трудно да се изчисли. Отпадане от точка М 1 до точка М, топката ще изразходва малко потенциална енергия. Тази загуба на енергия е равна на произведението от теглото на топката мг(м -- маса на топката, ж-- ускорение на гравитацията) до „загуба на височина“, т.е. от разликата във височината на топката в позиции М 1 и М,Освен това височините се измерват от определено ниво, например от нивото на земята. От каквото и ниво да се броят височините, тяхната разлика в нашия случай ще бъде равна на сегмента NM. Така че загубата на потенциална енергия на топката ще бъде равна на мг· H.M..

Но поради закона за запазване на енергията, загубената потенциална енергия на топката ще се превърне в кинетичната енергия на нейното движение, равна, както е известно, ако обозначим все още неизвестната скорост на топката. Приравнявайки тази кинетична енергия към загубената потенциална енергия, получаваме уравнението

от което веднага намираме стойността на желаната скорост

Посоката на тази скорост също е лесна за определяне. Тя ще бъде насочена тангенциално към циклоидата, т.е. по акорда М.Л.(фиг. 6.2), където Л- „най-ниската“ точка на генериращия кръг.

Ще ни интересува не толкова самата скорост, колкото нейната вертикална проекция, т.е. „скорост на спускане на топката“, скоростта на промяна на нейната височина. Тази вертикална проекция е лесна за изчисляване: тя е равна на къде е ъгълът между хордата М.Л.и вертикално. Акорд ATкръг с център ОТНОСНО, очевидно равен и успореден на хордата М.Л., и следователно ъгълът LMPравен на ъгъл KAT, както е отбелязано на фиг. 6.2. Така:

Ще сравним неравномерното движение по циклоида с равномерно движение по окръжност. За целта ще построим спомагателна окръжност така: през върха Ациклоидите са начертани перпендикулярно AD(диаметър на кръг с център ОТНОСНО), а през началната точка M 1 на движението на топката се прекарва успоредник M 1 B към нейната основа. Нека точката на пресичане на тези паралели и перпендикуляри е обозначена с буквата IN. Кръг, изграден върху AB, както на диаметъра, и ще бъде необходимата спомагателна окръжност. Все още не е ясно защо точно той е по-добър от другите кръгове.

Нека започнем със свързването на вертикалния компонент на скоростта на топката с елементите на спомагателния кръг. Ние имаме:

защото NM = VC.От триъгълник ДЕЙСТВАЙполучаваме:

Но АТ=2а cos , и следователно

Нека заместим намерената косинусова стойност в израза за Г-Н, отбелязани със звездичка (*). Получаваме:

Последният корен е равен на средната пропорционална между отсечките VCИ АК, т.е. между сегментите на хипотенузата ABтриъгълник ABC, на които последният е разделен по височина SK. Но тази средна пропорционална, според добре известната теорема за пропорционалните прави в правоъгълен триъгълник, е равна точно на височината SK:

VK·AK=SK 2 .

Следователно за вертикалния компонент Г-Нскоростта на движение на топката по циклоидата, която накрая получаваме:

MP=· КС.

Количества а И ж дадено ни от самото начало и несвързано с никоя точка М,нито с първоначалното си положение М 1 . По този начин движението на топката по циклоидата се определя изцяло от хордата KSспомагателен кръг, т.е. в крайна сметка позицията на точката СЪСна този кръг.

Помислете за равномерното движение на точка СЪСпо спомагателния кръг с ъглова скорост радиани в секунда, т.е. градуса в секунда. В този случай скоростта на точката СЪСпо окръжността ще бъде равна на произведението от радиуса на окръжността и ъгловата скорост, изразена в радиани (за секунда), т.е. равна на

С каква скорост се спуска точката? СЪС, с каква скорост се променя разстоянието му от права линия? М 0 М? 0 с равномерно движение на точка СЪСоколо обиколката? Не е трудно да се изчисли.

Скорост движението на точка върху окръжност е насочено тангенциално към окръжността, т.е. перпендикулярно на радиуса. Проекцията му върху вертикалата е равна на самата скорост умножено по косинуса на ъгъла на фиг. 6.3. Но ъгълът очевидно е равен на ъгъла КСО 1: и двете се получават чрез изваждане на ъгъла ОТНОСНО 1 SEот прав ъгъл. Косинус на ъгъл КСО 1 е равно . За вертикалната проекция на скоростта на равномерно движение в кръг намираме:

Получава се забележителен резултат: когато една точка се движи равномерно около окръжност, нейната проекция върху вертикалата се движи точно по същия начин, както проекцията върху вертикалата на топка, търкаляща се по циклоида. Проекциите на двете скорости във всеки момент от времето са равни една на друга. Но от това следва, че точката на окръжността от IN V Аи топка на циклоида от М 1 инч Аще пристигне по едно и също време. Това време се определя лесно. Вече казахме, че точка от спомагателния кръг прави радиан секунда, с други думи, тя ще обърне един радиан за секунди и един радиан за секунди. Нашата топка се нуждае от точно същото време, за да се търкулне надолу по циклоидата от точката М 1 до точка А. Също толкова време ще му отнеме да се издигне до точката по инерция. М? 1 , същият - да слезе отново, и същият - да се издигне и да се върне в изходна позиция (до т. М 1). Това означава, че времето на пълно трептене на топката (период на трептене) ще бъде равно на:

Това е много прекрасна формула. Виждаме, че периодът на движение на топката по циклоидалния жлеб се определя изцяло от размера на жлеба (радиуса на генериращата окръжност на циклоидата) и ускорението на гравитацията. Точкова позиция М 1 върху циклоида, нейното разстояние от права линия М 0 М? 0 няма значение. Без значение от коя точка на циклоидата започне да се движи топката, периодът на нейното трептене ще бъде един и същ.

Хюйгенс мисли как да използва тавтохроничното свойство на циклоида, за да създаде „перфектно“ махало. Как да накараме топката на махалото да се движи тавтохронно, без да прибягваме до жлебове и подобни устройства с високо триене? Мислейки за това, Хюйгенс стигна до понятията еволюта и еволвента.

Нека направим шаблон, състоящ се от две еднакви полуарки на циклоида, имащи обща върхова точка ОТНОСНО(фиг. 6.4). Нека обозначим радиуса на генериращата окръжност, както винаги, с а. Ще укрепим шаблона вертикално и в точката на връщане ОТНОСНОзавържете конец, равен на дължина на 4 а-- т.е. два пъти диаметъра на генериращата окръжност на циклоидата. Свободен край на нишката TНие ще ви предоставим тежка топка.

Топката ще опише развитието на циклоида по време на нейното движение АСОЕВ, защото нишката ще се увие около шаблона. Но развитието на една циклоида е точно същата циклоида. Така че кривата VMTRAпо която се движи топката ще бъде циклоида, генерирана от окръжност с радиус а.

Ако поставим топката в произволна точка Ми го остави на себе си, той ще започне да трепти и периодът на тези трептения няма да зависи от избора на точка М. Дори ако под въздействието на триене и съпротивление на въздуха обхватът на трептенията намалява, времето на трептене на махалото остава непроменено. Наистина това махало ще бъде тавтохронно!

Нека сега разгледаме малките трептения на махалото по дъга ABциклоиди (фиг. 6.5). Ако тези колебания са много малки, тогава влиянието на направляващия шаблон практически няма да се усети и махалото ще се движи почти като обикновено дълго махало л=4а, спряно в точка ОТНОСНО. Пътека ABциклоидното махало практически няма да се различава от пътя SEкръгло махало с дължина 4 а. Това означава, че периодът на малки трептения на обикновено кръгово махало с дължина л=4а практически няма да се различава от периода на циклоидното махало. Въвеждане във формулата

които срещнахме по-горе, вместо аравен на него, получаваме израз за периода на малки трептения на кръгово махало по отношение на неговата дължина:

ЗАКЛЮЧЕНИЕ

В процеса на завършване на курсовата си работа изучавах материали по темата за циклоидата, изучавах характеристиките на най-доброто махало, сравнявах доста елегантно, но не много просто изследване на циклоидата преди появата на интегралното смятане, с най- прост и познат, изучаван в диференциална геометрия и математически анализ; за пореден път се убеди в необходимостта от изучаване на тези дисциплини. Както се оказа, циклоидът има огромно практическо приложение не само в математиката, но и в технологичните изчисления и физиката.

Работата по изучаването на тази тема се оказа доста вълнуваща и интересна.

БИБЛИОГРАФИЯ

1. Берман Г.Н. Циклоид. -М., 2007. -113 с.

2. Савелов А.А. Плоски извивки. - М., 1960. - 293 с.

3. Фихтенголц Г.М. Основи на математическия анализ. -М., 2005, том 2. -464 с.

Публикувано на Allbest.ru

...

Подобни документи

Кратка история на изследването на циклоида. Геометрична дефиниция, свойства и характеристики на конструкцията на циклоида. Параметрично циклоидно уравнение и уравнение в декартови координати. Задачи за намиране на части от циклоида и фигури, образувани от циклоида.

курсова работа, добавена на 16.01.2011 г

Моменти и масови центрове на равнинни криви. Теорема на Гулден. Площта на повърхността, образувана от въртенето на дъга на равнинна крива около ос, лежаща в равнината на дъгата и не пресичаща я, е равна на произведението на дължината на дъгата и дължината на окръжността.

лекция, добавена на 09/04/2003

Определение на определен интеграл, неговите свойства. Дължина на дъгата на кривата. Площ на извит трапец. Повърхностна площ на въртене. Области на фигури, ограничени от графики на функции, ограничени от линии, дадени от уравнения. Изчисляване на обеми на тела.

тест, добавен на 02/10/2017

Определен интеграл е адитивен монотонен нормализиран функционал, дефиниран върху набор от двойки, неговите компоненти и свойства. Изчисляване на определен интеграл; Формула на Нютон-Лайбниц. Геометрични приложения: площ, дължина на дъга, обем на ротационно тяло.

презентация, добавена на 30.05.2013 г

Намиране на площта на фигура, ограничена от графики на функции с помощта на двоен интеграл. Получаване чрез завъртане на обема на тяло около оста OX на фигура, ограничена от посочените линии. Граници на интегриране в двоен интеграл върху област, ограничена от прави.

тест, добавен на 28.03.2014 г

Забележителни линии от 3-ти ред: декартов лист, диоклов цисоид, стофрид, Agnesi versière. Линии от четвърти и по-висок ред и някои трансцендентални линии: Архимедова спирала, кривата на най-късия низход. Районът на района, ограничен от лемниската.

курсова работа, добавена на 08/07/2015

Понятие за определен интеграл, изчисляване на площ, обем на тяло и дължина на дъгата, статичен момент и център на тежестта на кривата. Изчисляване на площ в случай на правоъгълна извита област. Приложение на криволинейни, повърхностни и тройни интеграли.

курсова работа, добавена на 19.05.2011 г

Производна на определен интеграл по отношение на променлива горна граница. Изчисляване на определения интеграл като граница на интегралната сума по формулата на Нютон–Лайбниц, промяна на променлива и интегриране по части. Дължина на дъгата в полярна координатна система.

тест, добавен на 22.08.2009 г

История на интегралното и диференциалното смятане. Приложения на определен интеграл при решаването на някои задачи по механика и физика. Моменти и масови центрове на равнинни криви, теорема на Гулден. Диференциални уравнения. Примери за решаване на задачи в MatLab.

резюме, добавено на 09/07/2009

Криволинейни интеграли от първи и втори род. Площта на региона, оградена от затворена крива. Обемът на тяло, образувано от въртене на затворена крива. Център на масата и инерционни моменти на кривата. Магнитно поле около проводник, по който тече ток. Същността на закона на Фарадей.

Където T?

| r(t)|===2 грях

Анализираните примери ни помогнаха да свикнем с новите понятия за еволюта и еволвента. Сега сме достатъчно подготвени да изследваме развитието на циклоидалните криви.

Докато изучавахме тази или онази крива, често изграждахме спомагателна крива - „придружител“ на тази крива.

Ориз. 89. Циклоид и съпътстващият го.

И така, построихме конхоиди на права линия и окръжност, развитие на окръжност, синусоида - спътник на циклоида. Сега, въз основа на тази циклоида, ще построим спомагателна циклоида, неразривно свързана с нея. Оказва се, че съвместното изследване на такава двойка циклоиди е в някои отношения по-просто от изследването на един отделен циклоид. Ще наричаме такава спомагателна циклоида придружаваща циклоида.

Нека разгледаме половината от арката на циклоидата AMB (фиг. 89). Не трябва да се смущаваме, че тази циклоида е разположена по необичаен начин („с главата надолу“).

Нека начертаем 4 прави линии, успоредни на водещата линия AK на разстояния a, 2a, 3a и 4a. Нека построим генерираща окръжност в позицията, съответстваща на точка M (на фиг. 89 центърът на тази окръжност е обозначен с буквата O). Нека означим ъгъла на завъртане на MON с . Тогава отсечката AN ще бъде равна (ъгълът се изразява в радиани).

Продължаваме диаметъра NT на образуващата окръжност отвъд точка T до пресечната точка (в точка E) с права линия PP. Използвайки TE като диаметър, ще построим кръг (с център). Нека построим допирателна в точка M към циклоидата AMB. За да направите това, точка M трябва, както знаем, да бъде свързана с точка T (стр. 23). Нека продължим допирателната MT отвъд точка T, докато се пресече с помощната окръжност и наричаме пресечната точка . Това е точката, която сега искаме да разгледаме.

Означихме ъгъла MON със Следователно ъгълът MTN ще бъде равен на (вписания ъгъл, базиран на същата дъга). Триъгълникът очевидно е равнобедрен. Следователно не само ъгълът, но и всеки ъгъл ще бъде равен.Така точно радиани остават за частта от ъгъла в триъгълника (не забравяйте, че ъгъл от 180° е равен на радиани). Също така отбелязваме, че сегментът NK очевидно е равен на a ().

Нека сега разгледаме кръга с център, показан на фиг. 89 пунктирана линия. От чертежа става ясно какъв кръг е това. Ако го търкаляте, без да се плъзгате по правата CB, тогава неговата точка B ще опише циклоидата BB. Когато пунктираната окръжност се завърти през ъгъла, центърът ще стигне до точката и радиусът ще заеме позицията Така точката, която построената се оказва точка от циклоидата BB,

Описаната конструкция свързва всяка точка M от циклоидата AMB с точка от циклоидата На фиг. 90 това съответствие е показано по-ясно. Получената по този начин циклоида се нарича придружаваща. На фиг. 89 и 90, циклоидите, изобразени с дебели прекъснати линии, са придружаващи по отношение на циклоидите, изобразени с дебели плътни линии.

От фиг. 89 е ясно, че правата е нормална в точка към придружаващата циклоида. Наистина, тази права минава през точката на циклоидата и през точката T на допиране на образуващата окръжност и насочващата линия („най-долната“ точка на образуващата окръжност, както казахме някога; сега се оказа, че това е „най-висок“, защото чертежът е завъртян).

Но същата права линия, по конструкция, е допирателна към „главната“ циклоида AMB. По този начин оригиналната циклоида се докосва до всяка нормала на придружаващата циклоида. Това е обвивката за нормалите на придружаващата циклоида, т.е. нейната еволюта. И „придружаващата“ циклоида се оказва просто еволвента (разгъната) на оригиналната циклоида!

Ориз. 91 Съответствие между точките на циклоидата и придружаващата я.

Като се включихме в тази тромава, но по същество проста конструкция, ние доказахме една забележителна теорема, открита от холандския учен Хюйгенс. Ето тази теорема: еволютата на една циклоида е точно същата циклоида, само изместена.

Нека обърнем внимание на факта, че при доказването на теоремата на Хюйгенс не използвахме нито безкрайно малки, нито неделими, нито приблизителни оценки. Ние дори не използвахме механика; понякога използвахме изрази, заимствани от механиката. Това доказателство е напълно в духа на разсъжденията, използвани от учените от 17 век, когато те искат да обосноват стриктно получените резултати, използвайки различни водещи съображения.

Едно важно следствие непосредствено следва от теоремата на Хюйгенс. Разгледайте сегмента AB на фиг. 89. Дължината на този сегмент очевидно е 4a. Нека сега си представим, че нишка е навита около дъгата AMB на циклоидата, фиксирана в точка A и оборудвана с молив в точка B. Ако „навием“ нишката, моливът ще се движи по протежение на циклоидата AMB , т.е. по циклоидата BMB.

Ориз. 91 Последователни еволюции на циклоидата.

Дължината на нишката, равна на дължината на полуарката на циклоида, очевидно ще бъде равна на сегмента AB, т.е., както видяхме, 4a. Следователно дължината на цялата дъга на циклоида ще бъде равна на 8а и формулата вече може да се счита за доста строго доказана.

От фиг. 89 можете да видите повече: формулата не само за дължината на цялата дъга на циклоидата, но и за дължината на всяка от нейните дъги. Наистина, очевидно е, че дължината на дъгата MB е равна на дължината на отсечката, т.е. двойната допирателна отсечка в съответната точка на циклоидата, съдържаща се вътре в образуващата окръжност.

5. Параметрично циклоидно уравнение и уравнение в декартови координати

Да приемем, че ни е дадена циклоида, образувана от окръжност с радиус a с център в точка A.

Ако изберем като параметър, определящ позицията на точката, ъгъла t=∟NDM, през който е успял да се завърти радиусът, който е имал вертикално положение AO в началото на търкалянето, тогава координатите x и y на точка M ще да се изрази, както следва:

x= OF = ON - NF = NM - MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

Така че параметричните уравнения на циклоидата имат формата:

Когато t се промени от -∞ до +∞, ще се получи крива, състояща се от безкраен брой разклонения като тези, показани на тази фигура.

Също така, в допълнение към параметричното уравнение на циклоида, има и неговото уравнение в декартови координати:

Където r е радиусът на окръжността, образуваща циклоидата.

6. Задачи за намиране на части от циклоида и фигури, образувани от циклоида

Задача No1. Намерете площта на фигура, ограничена от една дъга на циклоида, чието уравнение е дадено параметрично

и оста Ox.

Решение. За да решим този проблем, ще използваме фактите, които знаем от теорията на интегралите, а именно:

Площ на извит сектор.

Да разгледаме някаква функция r = r(ϕ), дефинирана върху [α, β].

ϕ 0 ∈ [α, β] съответства на r 0 = r(ϕ 0) и следователно точката M 0 (ϕ 0 , r 0), където ϕ 0,

r 0 - полярни координати на точката. Ако ϕ се промени, „преминавайки“ през целия [α, β], тогава променливата точка M ще опише някаква крива AB, дадена

уравнение r = r(ϕ).

Определение 7.4. Криволинейният сектор е фигура, ограничена от два лъча ϕ = α, ϕ = β и крива AB, дефинирана в полярна

координати по уравнението r = r(ϕ), α ≤ ϕ ≤ β.

Вярно е следното

Теорема. Ако функцията r(ϕ) > 0 и е непрекъсната върху [α, β], тогава площта

криволинейният сектор се изчислява по формулата:

Тази теорема беше доказана по-рано в темата за определен интеграл.

Въз основа на горната теорема, нашият проблем за намиране на площта на фигура, ограничена от една дъга на циклоида, чието уравнение е дадено от параметричните параметри x= a (t – sin t), y= a (1 – cos t), и оста Ox, се редуцира до следното решение.

Решение. От уравнението на кривата dx = a(1−cos t) dt. Първата дъга на циклоидата съответства на промяна на параметъра t от 0 до 2π. следователно

Задача No2. Намерете дължината на една дъга от циклоидата

Следната теорема и следствието от нея също бяха изучавани в интегралното смятане.

Теорема. Ако кривата AB е дадена от уравнението y = f(x), където f(x) и f ’ (x) са непрекъснати върху , тогава AB е поправима и

Последица. Нека AB е дадено параметрично

L AB = (1)

Нека функциите x(t), y(t) са непрекъснато диференцируеми върху [α, β]. Тогава

формула (1) може да бъде записана по следния начин

Нека направим промяна на променливите в този интеграл x = x(t), тогава y’(x)= ;

dx= x’(t)dt и следователно:

Сега да се върнем към решаването на нашия проблем.

Решение. Имаме и следователно

Задача No3. Трябва да намерим повърхността S, образувана от въртенето на една дъга на циклоидата

L=((x,y): x=a(t – sin t), y=a(1 – цена), 0≤ t ≤ 2π)

В интегралното смятане има следната формула за намиране на площта на повърхността на въртящо се тяло около оста x на крива, дефинирана параметрично на сегмент: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)

Прилагайки тази формула към нашето циклоидно уравнение, получаваме:

Задача No4. Намерете обема на тялото, получено при завъртане на арката на циклоида

По оста Окс.

В интегралното смятане, когато се изучават обеми, има следната забележка:

Нека използваме тази формула, за да намерим обема, от който се нуждаем.

Проблемът е решен.

Заключение

И така, в хода на тази работа бяха изяснени основните свойства на циклоидата. Научихме също как да построим циклоида и открихме геометричното значение на циклоида. Както се оказа, циклоидът има огромно практическо приложение не само в математиката, но и в технологичните изчисления и физиката. Но циклоидът има и други достойнства. Използван е от учени от 17-ти век при разработването на техники за изучаване на криви линии - онези техники, които в крайна сметка доведоха до изобретяването на диференциалното и интегралното смятане. Това беше и един от „пробните камъни“, върху които Нютон, Лайбниц и техните ранни изследователи изпробваха силата на мощни нови математически методи. И накрая, проблемът с брахистохрона доведе до изобретяването на вариационното смятане, което е толкова необходимо за днешните физици. Така циклоидът се оказва неразривно свързан с един от най-интересните периоди в историята на математиката.

Литература

1. Берман Г.Н. Циклоид. – М., 1980

2. Веров С.Г. Брахистохрон или друга тайна на циклоида // Quantum. – 1975. - № 5

3. Веров С.Г. Тайните на циклоидата // Quantum. – 1975. - № 8.

4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С., Радченко Т.Н. Приложения на определен интеграл. Методически указания и индивидуални задания за студенти от 1 курс на Физическия факултет. - Ростов n/a: UPL RSU, 1994.

5. Гиндикин С.Г. Звездната възраст на циклоида // Quantum. – 1985. - № 6.

6. Фихтенголц Г.М. Курс по диференциално и интегрално смятане. Т.1. – М., 1969

Тази линия се нарича "плик". Всяка крива линия е обвивка на своите допирателни.

Материята и движението, както и методът, който те представляват, позволяват на всеки да реализира своя потенциал в познанието на истината. Разработването на методология за развитие на диалектико-материалистичната форма на мислене и овладяването на подобен метод на познание е втората стъпка към решаването на проблема за развитието и реализацията на човешките способности. Фрагмент XX Възможности...

В тази ситуация хората могат да развият неврастения - невроза, основата на клиничната картина на която е астенично състояние. Както в случай на неврастения, така и в случай на декомпенсация на неврастенична психопатия, същността на умствената (психологическа) защита се отразява в отдръпването от затруднения в раздразнителна слабост с вегетативни дисфункции: или човекът несъзнателно "се бори" повече с атаката. ..

Различни видове дейности; развитие на пространствено въображение и пространствени понятия, образно, пространствено, логическо, абстрактно мислене на учениците; развиване на способността за прилагане на геометрични и графични знания и умения за решаване на различни приложни задачи; запознаване със съдържанието и последователността на етапите на проектните дейности в областта на техническите и...

дъги. Спиралите също са еволвенти на затворени криви, например еволвента на окръжност. Имената на някои спирали се дават от сходството на техните полярни уравнения с уравненията на криви в декартови координати, например: · параболична спирала (a - r)2 = bj, · хиперболична спирала: r = a/j. · Прът: r2 = a/j · si-ci-спирала, параметричните уравнения на която имат формата: , )