Хармоничните трептения възникват според закона:
х = А cos(ω T + φ 0),
Където х– изместване на частицата от равновесното положение, А– амплитуда на трептенията, ω – кръгова честота, φ 0 – начална фаза, T- време.
Период на трептене T = .
Скорост на осцилираща частица:
υ
=
 = – Аω sin(ω T
+ φ 0),
= – Аω sin(ω T
+ φ 0),
ускорение а
=
 = –Аω 2 cos (ω T
+ φ 0).
= –Аω 2 cos (ω T
+ φ 0).
Кинетична енергия на частица, подложена на трептящо движение: д k =  =
= грях 2 (ω T+ φ 0).
грях 2 (ω T+ φ 0).
Потенциална енергия:
д n=  cos 2 (ω T
+ φ 0).
cos 2 (ω T
+ φ 0).
Периоди на трептене на махалото
– пролет T
=
 ,
,
Където м– маса на товара, к– коефициент на твърдост на пружината,
– математически T
=
 ,
,
Където л– дължина на окачването, ж- ускорение на гравитацията,
– физически T
=
 ,
,
Където аз– инерционен момент на махалото спрямо оста, минаваща през точката на окачване, м– маса на махалото, л– разстояние от точката на окачване до центъра на масата.
Намалената дължина на физическо махало се намира от условието: л np =  ,
,
Обозначенията са същите като за физическо махало.
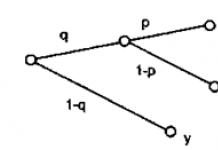
Когато се добавят две хармонични трептения с еднаква честота и една посока, се получава хармонично трептене със същата честота с амплитуда:
А = А 1 2 + А 2 2 + 2А 1 А 2 cos(φ 2 – φ 1)
и начална фаза: φ = арктан  .
.
Където А 1 , А 2 – амплитуди, φ 1, φ 2 – начални фази на нагънати трептения.
Траекторията на полученото движение при добавяне на взаимно перпендикулярни трептения със същата честота:
 +
+
 –
–
 cos (φ 2 – φ 1) = sin 2 (φ 2 – φ 1).
cos (φ 2 – φ 1) = sin 2 (φ 2 – φ 1).
Затихналите трептения възникват съгласно закона:
х = А 0 д - β T cos(ω T + φ 0),
където β е коефициентът на затихване, значението на останалите параметри е същото като за хармоничните трептения, А 0 – начална амплитуда. В даден момент Tамплитуда на вибрациите:
А = А 0 д - β T .
Логаритмичният декремент на затихване се нарича:
λ = дневник  = β T,
= β T,
Където T– период на трептене: T
=
 .
.
Качественият фактор на една осцилаторна система се нарича:
Уравнението на равнинна движеща се вълна има формата:
г = г 0 cos ω( T ± ),
Където при– изместване на осцилиращото количество от равновесното положение, при 0 – амплитуда, ω – ъглова честота, T- време, х– координата, по която се разпространява вълната, υ – скорост на разпространение на вълната.
Знакът "+" съответства на вълна, разпространяваща се срещу оста х, знакът „–“ съответства на вълна, разпространяваща се по оста х.
Дължината на вълната се нарича нейният пространствен период:
λ = υ T,
Където υ – скорост на разпространение на вълната, T– период на разпространяващи се трептения.
Вълновото уравнение може да бъде написано:
г = г 0 cos 2π (+).
Стоящата вълна се описва с уравнението:
г
= (2г 0cos  ) cos ω T.
) cos ω T.
Амплитудата на стоящата вълна е оградена в скоби. Точките с максимална амплитуда се наричат антиноди,
х n = н ,
точки с нулева амплитуда - възли,
х y = ( н + ) .
Примери за решаване на проблеми
Проблем 20
Амплитудата на хармоничните трептения е 50 mm, периодът е 4 s и началната фаза . а) Запишете уравнението на това трептене; б) намерете изместването на осцилиращата точка от равновесното положение при T=0 и при T= 1.5 s; в) начертайте графика на това движение.
Решение
Уравнението на трептенията се записва като х = а cos( T+ 0).
Според условието е известен периодът на трептене. Чрез него можем да изразим кръговата честота =
 .
Останалите параметри са известни:
.
Останалите параметри са известни:
а) х= 0,05cos( T + ).
б) Офсет хпри T= 0.
х 1 = 0,05 cos = 0,05
 = 0,0355 m.
= 0,0355 m.
При T= 1,5 s
х 2 = 0,05 cos( 1,5 + )= 0,05 cos = – 0,05 m.
V  ) графика на функция х=0,05cos ( T
+
) както следва:
) графика на функция х=0,05cos ( T
+
) както следва:
Да определим позицията на няколко точки. Известен х 1 (0) и х 2 (1.5), както и периода на трептене. И така, чрез T= 4 s стойност хповторения, а след T = 2 s променя знака. Между максимума и минимума в средата е 0.
Проблем 21
Точката извършва хармонично трептене. Периодът на трептене е 2 s, амплитудата е 50 mm, началната фаза е нула. Намерете скоростта на точката в момента, когато нейното отместване от равновесното положение е 25 mm.
Решение
1 начин. Записваме уравнението на точковото трептене:
х= 0,05 cos T,
тъй като =
 =.
=.
Намиране на скоростта в момента T:
υ
=
 = – 0,05
cos T.
= – 0,05
cos T.
Намираме момента във времето, когато преместването е 0,025 m:
0,025 = 0,05 cos T 1 ,
следователно cos T 1 = , T 1 = . Заменяме тази стойност в израза за скорост:
υ
= – 0,05 sin
=
– 0,05
 = 0,136 m/s.
= 0,136 m/s.
Метод 2. Обща енергия на осцилаторно движение:
д
=
 ,
,
Където А– амплитуда, – кръгова честота, м – маса на частиците.
Във всеки момент от времето тя се състои от потенциалната и кинетичната енергия на точката
д k =
 ,
д n =
,
д n =
 , Но к
= м 2, което означава д n =
, Но к
= м 2, което означава д n =
 .
.
Нека напишем закона за запазване на енергията:
 =
=
 +
+ ,
,
от тук получаваме: а 2 2 = υ 2 + 2 х 2 ,
υ
=
 =
=
 = 0,136 m/s.
= 0,136 m/s.
Проблем 22
Амплитуда на хармоничните трептения на материална точка А= 2 см, обща енергия д= 3∙10 -7 J. При какво преместване от равновесното положение действа силата върху трептящата точка Е = 2,25∙10 -5 N?
Решение
Общата енергия на точка, извършваща хармонични трептения, е равна на:
д
=
 .
(13)
.
(13)
Модулът на еластичната сила се изразява чрез изместването на точки от равновесното положение хпо следния начин:
Е = k x (14)
Формула (13) включва маса ми кръгова честота , а в (14) – коефициентът на коравина к. Но кръговата честота е свързана с мИ к:
2 =
 ,
,
оттук к
= м 2 и F = м 2 х. Като изрази м 2 от връзка (13) получаваме:
м 2 =
 ,
Е
=
,
Е
=
 х.
х.
Откъде получаваме израза за преместването х:
х
=
 .
.
Заместването на числовите стойности дава:
х
=
 = 1,5∙10 -2 m = 1,5 cm.
= 1,5∙10 -2 m = 1,5 cm.
Проблем 23
Точката участва в две трептения с еднакви периоди и начални фази. Амплитуди на трептене А 1 = 3 см и A 2 = 4 см. Намерете амплитудата на резултантното трептене, ако: 1) трептенията възникват в една посока; 2) вибрациите са взаимно перпендикулярни.
Решение
Ако се появят трептения в една посока, тогава амплитудата на получените трептения се определя като:
Където А 1 и А 2 – амплитуди на добавени трептения, 1 и 2 – начални фази. Според условието началните фази са еднакви, което означава 2 – 1 = 0 и cos 0 = 1.
Следователно:
А
=
 =
= =
А 1 +А 2 = 7 см.
=
А 1 +А 2 = 7 см.
Ако трептенията са взаимно перпендикулярни, тогава уравнението на резултантното движение ще бъде:
 cos( 2 – 1) = sin 2 ( 2 – 1).
cos( 2 – 1) = sin 2 ( 2 – 1).
Тъй като по условие 2 – 1 = 0, cos 0 = 1, sin 0 = 0, уравнението ще бъде записано като:  =0,
=0,
или  =0,
=0,
или  .
.

Получената връзка между хИ приможе да се изобрази на графика. Графиката показва, че резултатът ще бъде трептене на точка върху права линия MN. Амплитудата на това трептене се определя като: А
=
 = 5 см.
= 5 см.
Задача 24
Период затихващи трептения T=4 s, логаритмичен декремент на затихване = 1,6, началната фаза е нула. Преместване на точка при T = равно на 4,5 см. 1) Напишете уравнението на това трептене; 2) Постройте графика на това движение за два периода.
Решение
Уравнението на затихналите трептения с нулева начална фаза има формата:
х = А 0 д - T cos2 .
Няма достатъчно първоначални стойности на амплитудата, за да се заменят цифровите стойности А 0 и коефициент на затихване .
Коефициентът на затихване може да се определи от съотношението за логаритмичния декремент на затихване:
= T.
Така =
=
 = 0,4 s -1 .
= 0,4 s -1 .
Първоначалната амплитуда може да се определи чрез заместване на второто условие:
4,5 см = А 0
 cos 2
cos 2  = А 0
= А 0
 cos = А 0
cos = А 0

 .
.
От тук намираме:
А 0
=
4,5∙
 (cm) = 7,75 cm.
(cm) = 7,75 cm.
Крайното уравнение на движението е:
х
= 0,0775
 цена.
цена.


Задача 25
Какъв е логаритмичният декремент на затихване на математическо махало, ако за T = 1 мин. амплитудата на трептенията намалява наполовина? Дължина на махалото л = 1 м.
Решение
Логаритмичният декремент на затихване може да се намери от връзката: = T,
където е коефициентът на затихване, T– период на трептене. Естествена кръгова честота на математическо махало:
0
=
 = 3,13 s -1 .
= 3,13 s -1 .
Коефициентът на затихване на трептенията може да се определи от условието: А 0 = А 0 д - T ,
T= ln2 = 0,693,
=
 = 0,0116c -1.
= 0,0116c -1.
Тъй като << 0 ,
то
в формуле
=
 може да се пренебрегне в сравнение с 0 и периодът на трептене може да се определи по формулата:
T
=
може да се пренебрегне в сравнение с 0 и периодът на трептене може да се определи по формулата:
T
=
 = 2c.
= 2c.
Заменяме и Tв израза за логаритмичния декремент на затихване и получаваме:
= T= 0,0116 s -1 ∙ 2 s = 0,0232.
Задача 26
Уравнението на незатихващите трептения е дадено във формата х= 4 sin600 Tсм.
Намерете отместването от равновесното положение на точка, разположена на разстояние л= 75 см от източника на вибрации, през T= 0,01 s след началото на трептенето. Скорост на разпространение на трептенията υ = 300 m/s.
Решение
Нека запишем уравнението на вълна, разпространяваща се от даден източник: х= 0,04 sin 600 ( T– ).
Намираме фазата на вълната в този моментвреме на това място:
T–
= 0,01 – = 0,0075 ,
= 0,0075 ,
600 ∙ 0,0075 = 4,5,
sin 4,5 = sin = 1.
Следователно изместването на точката х= 0,04 m, т.е. на разстояние л =75 см от източника в даден момент T= 0,01 s максимално изместване на точката.
Библиография
Волкенштейн В.С.. Сборник задачи за общия курс по физика. – Санкт Петербург: Спецлит, 2001.
Савелиев И.В.. Сборник въпроси и задачи по обща физика. – М.: Наука, 1998.
Хармонично уравнение
Където Х -изместване на осцилиращата точка от равновесното положение;
T- време; а,ω, φ - съответно амплитуда, ъглова честота,
начална фаза на трептения; - фаза на трептения в момента T.
Ъглова честота
където ν и T са честотата и периодът на трептенията.
Скоростта на точка, извършваща хармонични трептения, е
Ускорение при хармонично трептене
Амплитуда Аполученото трептене, получено чрез събиране на две трептения с еднакви честоти, възникващи по една права линия, се определя по формулата
Където а 1 и А 2 - амплитуди на компонентите на вибрациите; φ 1 и φ 2 са началните им фази.
Началната фаза φ на полученото трептене може да се намери от формулата
![]()
Честотата на ударите, които възникват при добавяне на две трептения, възникващи по една права линия с различни, но сходни честоти ν 1 и ν 2,
Уравнение на траекторията на точка, участваща в две взаимно перпендикулярни трептения с амплитуди A 1 и A 2 и начални фази φ 1 и φ 2,
Ако началните фази φ 1 и φ 2 на компонентите на трептене са еднакви, тогава уравнението на траекторията приема формата
точката се движи по права линия.
В случай, че фазовата разлика е , уравнението
приема формата
точката се движи по елипса.
Диференциално уравнение на хармоничните трептения на материална точка
Или ,
където m е масата на точката; к-коефициент на квазиеластична сила ( к=Tω 2).
Общата енергия на материална точка, извършваща хармонични трептения, е
Периодът на трептене на тяло, окачено на пружина (пружинно махало)
Където м- телесна маса; к-твърдост на пружината. Формулата е валидна за еластични вибрации в границите, в които се изпълнява законът на Хук (при малка маса на пружината спрямо масата на тялото).
Период на трептене на математическо махало
Където л- дължина на махалото; g-ускорение на гравитацията. Период на трептене на физическо махало
Където Дж- инерционен момент на трептящото тяло спрямо оста
колебание; А- разстояние на центъра на масата на махалото от оста на трептене;
Намалена дължина на физическо махало.
Дадените формули са точни за случай на безкрайно малки амплитуди. За крайни амплитуди тези формули дават само приблизителни резултати. При амплитуди не по-големи от грешката в стойността на периода не надвишава 1%.
Периодът на усукващи вибрации на тяло, окачено на еластична нишка, е
Където J-инерционен момент на тялото спрямо оста, съвпадаща с еластичната нишка; к-твърдостта на еластична нишка, равна на съотношението на еластичния момент, възникващ, когато нишката е усукана, към ъгъла, под който нишката е усукана.
Диференциално уравнение на затихващите трептения ![]() , или ,
, или ,
Където r- коефициент на съпротивление; δ - коефициент на затихване: ; ω 0 - естествена ъглова честота на трептенията *
Уравнение на затихналите трептения
Където A(t)-амплитуда на затихналите трептения в момента T;ω е тяхната ъглова честота.
Ъглова честота на затихващите трептения
О Зависимост на амплитудата на затихващите трептения от времето
Където А 0 - амплитуда на трептенията в момента T=0.
Декремент на логаритмични колебания
![]()
Където A(t)И A (t+T) -амплитуди на две последователни трептения, разделени във времето с период.
Диференциално уравнение на принудените трептения
където е външната периодична сила, действаща върху
осцилираща материална точка и причиняваща принуд
флуктуации; F 0 -неговата амплитудна стойност;
Амплитуда на принудени трептения
Резонансна честота и резонансна амплитуда ![]() И
И
Примери за решаване на проблеми
Пример 1.Точката осцилира според закона x(t)= ,Където А=2вижте Определете началната фаза φ, ако
х(0)= cm и х , (0)<0. Построить векторную диаграмму для мо-
ченге T=0.
Решение. Нека използваме уравнението на движението и изразим преместването в момента T=0 през началната фаза:
От тук намираме началната фаза:
* В дадените по-горе формули за хармонични вибрации същата величина беше обозначена просто с ω (без индекс 0).
Нека заместим дадените стойности в този израз х(0) и A:φ=
= . Стойността на аргумента удовлетворява
две ъглови стойности:
За да решите коя от тези стойности на ъгъла φ удовлетворява
също отговаря на условието, нека първо намерим:
Заместване на стойността в този израз T=0 и алтернативни стойности
начални фази и , намираме
 Както винаги А>0 и ω>0, само тогава
Както винаги А>0 и ω>0, само тогава
до първата стойност на началната фаза.
По този начин необходимият начален
фаза
Въз основа на намерената стойност на φ, ние конструираме
тях векторна диаграма (фиг. 6.1).
Пример 2.Материална точка
маса T=5 g изпълнява хармонично
трептения с честота ν
=0,5 Hz.
Амплитуда на трептене А=3 см. Оп-
разделяне: 1) скорост υ точки в mo-
момент във времето, когато отместването x=
= 1,5 cm; 2) максимална якост
F max, действащ върху точка; 3)
Ориз. 6.1 обща енергия досцилираща точка
ki.
и получаваме формулата за скоростта, като вземем първата производна по време на изместването:
За да се изрази скоростта чрез преместване, е необходимо да се изключи времето от формули (1) и (2). За да направим това, поставяме на квадрат двете уравнения и разделяме първото на A 2,второто върху A 2 ω 2 и добавете:
Или ![]()
След като реши последното уравнение за υ , ще намерим
След като извършихме изчисления по тази формула, получаваме
Знакът плюс съответства на случая, когато посоката на скоростта съвпада с положителната посока на оста Х,знак минус - когато посоката на скоростта съвпада с отрицателната посока на оста Х.
Отместването по време на хармонично трептене, в допълнение към уравнението (1), може да се определи и чрез уравнението
Повтаряйки същото решение с това уравнение, получаваме същия отговор.
2. Намираме силата, действаща върху точка, използвайки втория закон на Нютон:
Където А -ускорение на точката, което получаваме, като вземем времевата производна на скоростта:
Замествайки израза на ускорението във формула (3), получаваме
Оттук и максималната стойност на силата
Замествайки стойностите на π, ν в това уравнение, TИ а,ще намерим
3. Общата енергия на осцилираща точка е сумата от кинетичната и потенциалната енергия, изчислени за всеки момент от времето.
Най-лесният начин за изчисляване на общата енергия е в момента, в който кинетичната енергия достигне максимална стойност. В този момент потенциална енергияравно на нула. Следователно общата енергия дточката на трептене е равна на максималната кинетична енергия
Определяме максималната скорост от формула (2), поставяйки
: . Заместване на израза за скорост във формата
mulu (4), да намерим
Замествайки стойностите на количествата в тази формула и правейки изчисления, получаваме
или µJ.
Пример 3. л= 1 m и маса м 3 =400 гр. подсилени малки топчета с маси м 1 = 200 gi м 2 =300гр. Прътът осцилира около хоризонтална ос, перпендикулярна
дикулярен на пръта и минаващ през средата му (точка O на фиг. 6.2). Определете период Tтрептения, направени от пръта.
Решение. Периодът на трептене на физическо махало, като прът с топки, се определя от съотношението
Където J- T -неговата маса; l C -разстоянието от центъра на масата на махалото до оста.
Инерционният момент на това махало е равен на сумата от инерционните моменти на топките Дж 1 и J2и прът Дж 3:
Вземане на топките за материални точки, нека изразим техните инерционни моменти:
Тъй като оста минава през средата на пръта, тогава
неговият инерционен момент спрямо тази ос Дж 3 =
= .
Заместване на получените изрази Дж 1 , J2И
Дж 3 във формула (2), намираме общия инерционен момент на fi-
статично махало:
След като извършихме изчисления по тази формула, намираме
Ориз. 6.2 Масата на махалото се състои от масите на топките и масата
прът:
Разстояние l CЩе намерим центъра на масата на махалото от оста на трептене въз основа на следните съображения. Ако оста хнасочете по пръта и подравнете началото на координатите с точката ОТНОСНО,след това необходимото разстояние лравна на координатата на центъра на масата на махалото, т.е.
Заместване на стойностите на количествата м 1 , м 2 , м, ли след извършване на изчисления намираме
След като направихме изчисления по формула (1), получаваме периода на трептене на физическо махало:
Пример 4.Физическото махало е прът
дължина л= 1 m и маса 3 T 1 сприкрепен към единия му край
диаметър и тегло на обръча T 1 .
Хоризонтална ос Оз
махалото минава през средата на пръта перпендикулярно на него (фиг. 6.3). Определете период Tтрептения на такова махало.
Решение. Периодът на трептене на физическо махало се определя по формулата
![]() (1)
(1)
 |
Където J-инерционен момент на махалото спрямо оста на трептене; T -неговата маса; л° С - разстоянието от центъра на масата на махалото до оста на трептене.
Инерционният момент на махалото е равен на сумата от инерционните моменти на пръта Дж 1 и обръч Дж 2:
Инерционният момент на пръта спрямо оста,
перпендикулярно на пръта и преминаване
чрез неговия център на масата, се определя от формата-
le . IN в такъв случай t= 3T 1 и
Ще намерим инерционния момент на обръча, използвайки
наречена теорема на Щайнер,
Където J-инерционен момент спрямо про-
произволна ос; J 0 -инерционен момент спрямо
спрямо оста, минаваща през центъра на масата
успоредна на дадена ос; А -разстояние
между посочените оси. С помощта на тази форма
муле до обръча, получаваме
| Ориз. 6.3 |
Заместване на изрази Дж 1 и Дж 2 във формула (2), намираме инерционния момент на махалото спрямо оста на въртене:
Разстояние l Cот оста на махалото до неговия център на масата е равно на
Заместване на изразите във формула (1) Дж, л s и масата на махалото, намираме периода на неговите трептения:
След като изчислим по тази формула, получаваме T=2,17 s.
Пример 5.Добавят се две трептения в една и съща посока
изразени с уравнения; x 2 =
= , където А 1 =
1 см, А 2 =2 cm, s, s, ω =
= . 1. Определете началните фази φ 1 и φ 2 на осцилаторните компоненти
Бания. 2. Намерете амплитудата Аи началната фаза φ на полученото трептене. Напишете уравнението за получената вибрация.
Решение. 1. Уравнението на хармоничната вибрация има формата
Нека преобразуваме уравненията, посочени в постановката на проблема, в същата форма:
От сравнение на изрази (2) с равенство (1) намираме началните фази на първото и второто колебание:
Радвам се и се радвам.
2. Да се определи амплитудата Ана полученото трептене е удобно да се използва векторната диаграма, представена в ориз. 6.4. Според косинусовата теорема получаваме
където е фазовата разлика между компонентите на трептенията.
Тъй като , тогава, замествайки намерените
стойностите на φ 2 и φ 1 са rad.
| Ориз. 6.4 |
Нека заместим стойностите А 1 , А 2 и във формула (3) и
Нека направим изчисленията:
А= 2,65 см.
Определя се тангенса на началната фаза φ на полученото трептене
лим директно от фиг. 6.4: ![]() , от
, от
да начална фаза
Нека заместим стойностите А 1 , А 2 , φ 1, φ 2 и извършете изчисленията:
Тъй като ъгловите честоти на добавените трептения са еднакви,
тогава полученото трептене ще има същата честота ω. Това
ни позволява да напишем уравнението на получената вибрация във формата
, Където А=2,65 cm, , рад.
Пример 6.Материалната точка участва едновременно в две взаимно перпендикулярни хармонични трептения, уравненията на които
Където а 1 =
1 см, А 2 = 2 см, . Намерете уравнението на траекторията на точката
ki. Изградете траектория, като спазвате мащаба и посочете
посока на движение на точката.
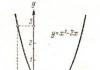
Решение. За да намерим уравнението за траекторията на точка, елиминираме времето Tот дадените уравнения (1) и (2). За да направите това, използвайте
Нека използваме формулата. В такъв случай
, Ето защо
Тъй като според формула (1)
, след това уравнението на траекторията
рис
Полученият израз е уравнението на парабола, чиято ос съвпада с оста оОт уравнения (1) и (2) следва, че преместването на точка по координатните оси е ограничено и варира от -1 до +1 cm по оста ои от -2 до +2 cm по оста OU.
За да конструираме траекторията, използваме уравнение (3), за да намерим стойностите y,съответстващ на диапазон от стойности Х,отговарящи на условието cm, и създайте таблица:
За да посочим посоката на движение на дадена точка, ще следим как нейната позиция се променя във времето. В началния момент T=0 координатите на точката са равни х(0)=1 cm и г(0)=2 см. В следващ момент от време, например когато T 1 =l s, координатите на точките ще се променят и ще се изравнят х(1)= -1 cm, y( T )=0. Познавайки позициите на точките в началния и следващите (близки) моменти от време, можете да посочите посоката на движение на точката по траекторията. На фиг. 6.5 тази посока на движение е обозначена със стрелка (от точката Акъм произхода). След момента T 2 = 2 s осцилиращата точка ще достигне точката Д,ще се движи в обратна посока.
Кинематика на хармоничните трептения
6.1.
Уравнението на точковите трептения има формата,
където ω=π s -1, τ=0,2 s. Определете период Tи начална фаза φ
колебание.
6.2.
Определете период T,честота v и начална фаза φ на трептенията, дадени от уравнението, където ω=2,5π s -1,
τ=0,4 s.
6.3.
Където А x(0)=2средства за масова информация
; 2) x(0) = cm и ; 3) x(0)=2cm и ; 4)
x(0)= и . Постройте векторна диаграма за
момент T=0.
6.4.
Точката се колебае според закона,
Където А=4 см. Определете началната фаза φ, ако: 1) x(0)=2средства за масова информация
; 2) х(0)= cm и ; 3) х(0)= cm и ;
4) х(0)= cm и . Постройте векторна диаграма за
момент T=0.
6.5.
Точката се колебае според закона,
Където А=2 см; ; φ= π/4 рад. Изграждане на графики на зависимости
от време: 1) изместване x(t); 2) скорост; 3) ускорение
6.6.
Точката трепти с амплитуда А=4 см и период T=2 s.Напишете уравнение за тези колебания, като приемете, че in
момент T=0 отместване x(0)=0И . Определете фазата
за два момента във времето: 1) когато преместването x= 1 см и ;
2) когато скорост = -6 cm/s и х<0.
6.7. Точката се движи равномерно по окръжността обратно на часовниковата стрелка с период T=6 s. Диаметър докръжност е 20 см. Напишете уравнението на движение на проекцията на точка върху оста Х,преминаващ през центъра на окръжността, ако в момента на времето, взет за начален, проекцията върху оста хравно на нула. Намерете отместване Х,скорост и ускорение на проекцията на точка в един момент t= 1s.
6.8. Определете максималните стойности на скоростта и ускорението на точка, извършваща хармонични трептения с амплитуда А= 3 см и ъглова честота
6.9.
Точката осцилира според закона, където А =
=5 см; . Определете ускорението на точка в момента,
когато скоростта му е = 8 cm/s.
6.10.
Точката извършва хармонични трептения. Най велик
пристрастие х m ah точка е 10 см, максимална скорост =
=20 cm/s. Намерете ъгловата честота ω на трептенията и максималното ускорение на точката.
6.11.
Максималната скорост на точка, извършваща хармонични трептения, е 10 cm/s, максималното ускорение =
= 100 cm/s 2 . Намерете ъгловата честота ω на трептенията, техния период T
и амплитуда А.Напишете уравнението на трептенията, като вземете началната фаза равна на нула.
6.12. Точката осцилира според закона. В даден момент от време изместването х 1 точка се оказа равна на 5 см. Когато фазата на трептене се удвои, преместването x стана равно на 8 см. Намерете амплитудата Аколебание.
6.13.
Точката осцилира според закона.
В даден момент от време изместването хточка е 5 см, нейната скорост
= 20 cm/s и ускорение = -80 cm/s 2. Намерете амплитудата А, ъглова честота ω, период Tтрептения и фаза в разглеждания момент от времето.
Добавяне на вибрации
6.14. Две еднакво насочени хармонични трептения с еднакъв период с амплитуди А 1 =10 cm и А 2 =6 cm се събират до една вибрация с амплитуда А= 14 см. Намерете фазовата разлика на добавените трептения.
6.15. Две хармонични трептения, насочени по една и съща права линия и имащи еднакви амплитуди и периоди, се събират в едно трептене със същата амплитуда. Намерете фазовата разлика на добавените трептения.
6.16.
Определете амплитудата Аи се получава началната фаза f
осцилираща вибрация, която възниква, когато се добавят две вибрации
същата посока и период: и
, Където А 1 =А 2 =1 cm; ω=π s -1; τ=0,5 s. Намерете уравнението на получената вибрация.
6.17.
Точката участва в две еднакво насочени трептения: и , където А 1 =
1 см; А 2 =2 cm; ω=
= 1 s -1 . Определете амплитудата Аполучената вибрация,
неговата честота v и начална фаза φ. Намерете уравнението на това движение.
6.18.
Добавят се две хармонични трептения от едно
царува с равни периоди T 1 =T 2 =1,5 s и амплитуди
А 1 =А 2 =
2см. Начални фази на трептения и. Определете амплитудата Аи началната фаза φ на полученото трептене. Намерете неговото уравнение и го съставете в мащаб
векторна диаграма на добавяне на амплитуда.
6.19. Добавят се три хармонични трептения с еднаква посока и равни периоди T 1 =T 2 =T 3 =2с и амплитуди А 1 =А 2 =А 3 =3 см. Начални фази на трептенията φ 1 =0, φ 2 =π/3, φ 3 =2π/3. Постройте векторна диаграма на добавяне на амплитуда. Определете амплитудата от чертежа Аи началната фаза φ на полученото трептене. Намерете неговото уравнение.
6.20.
Две хармонични трептения на едно и също
честота и същата посока: и х 2 =
= . Начертайте векторна диаграма за момента
време T=0. Определете аналитично амплитудата Аи начален
фаза φ на полученото трептене. Отложи Аи φ върху вектора
диаграма. Намерете уравнението на получената вибрация (в тригонометрична форма през косинуса). Решете задачата за двама
случаи: 1) А 1 =
1cm, φ 1 =π/3; А 2 =2 cm, φ 2 =5π/6; 2) A 1 = 1 см,
φ 1 =2π/3; А 2 =1 cm, φ 2 =7π/6.
6.21. Два камертона звучат едновременно. Честотите ν 1 и ν 2 на техните трептения са съответно 440 и 440,5 Hz. Определете период Tудари.
6.22.
Добавят се две взаимно перпендикулярни трептения,
изразени с уравненията и , където
А 1 =2
см, А 2 =1 cm, τ=0,5 s. Намерете уравнението на траекторията
и го изградете, показвайки посоката на движение на точката.
6.23.
Една точка извършва едновременно две хармонични трептения, протичащи във взаимно перпендикулярни посоки
и изразено чрез уравненията и ,
Където А 1 =
4 см, А 1 =8 cm, , τ=1 s. Намерете уравнението на траекторията на точката и постройте графика на нейното движение.
6.24. Една точка извършва едновременно две хармонични трептения с еднаква честота, протичащи във взаимно перпендикулярни посоки, изразени с уравненията: 1) и
Намерете (за осем случая) уравнението на траекторията на точка, конструирайте я в съответствие с мащаба и посочете посоката на движение. Приеми: А=2см, А 1 =3 см, А 2 = 1 см; φ 1 =π/2, φ 2 =π.
6.25
. Точката участва едновременно в две взаимно перпендикулярни трептения, изразени с уравненията и
, Където А 1 =
2 см, А 2 =1 см. Намерете уравнението на траекторията
точки и го конструирайте, като посочите посоката на движение.
6.26.
Една точка извършва едновременно две хармонични трептения, протичащи във взаимно перпендикулярни посоки
и се изразява с уравненията и , където А 1 =
=0,5 cm; А 2 =2 см. Намерете уравнението на траекторията на точката и построете
нея, указвайки посоката на движение.
6.27.
Движението на точка се дава от уравненията и y=
= , където А 1 =10 см, А 2 =5 cm, ω=2 s -1, τ=π/4 s. намирам
уравнение на траектория и скорост на точка в даден момент от време T=0,5 s.
6.28.
Една материална точка участва едновременно в две взаимно перпендикулярни трептения, изразени с уравненията
и къде А 1 =2
см, А 2 =1 см. Намерете
уравнение на траекторията и го съставете.
6.29. Точката участва едновременно в две хармонични трептения, възникващи във взаимно перпендикулярни посоки, описани от уравненията: 1) и
Намерете уравнението на траекторията на точката, конструирайте я в съответствие с мащаба и посочете посоката на движение. Приеми: А=2 см; А 1 =zсм.
6.30.
Точката участва едновременно в два взаимно перпендикулярни
куларни вибрации, изразени с уравнения и
y=A 2 sin 0,5ω T, Където А 1 = 2 см, А 2 =3 см. Да се намери уравнението на траекторията на точката и да се построи, като се посочи посоката на движение.
6.31. Преместването на светещата точка върху екрана на осцилоскопа е резултат от добавянето на две взаимно перпендикулярни трептения, които се описват с уравненията: 1) х=Агрях 3 ω TИ при=Агрях 2ω T; 2) х=Агрях 3ω TИ г=А cos 2ω T; 3) х=Агрях 3ω Tи y= А cos ω T.
Използвайки графичния метод на добавяне и наблюдавайки мащаба, изградете траекторията на светеща точка на екрана. Приеми А=4 см.
Динамика на хармоничните трептения. Махала
6.32. Материална точка с маса T=50 g претърпява трептения, чието уравнение има вида х=А cos ω T,Където А= 10 cm, ω=5 s -1. Намерете сила Е,действащи върху точка, в два случая: 1) в момента, когато фазата ω T=π/3; 2) в позицията на най-голямото изместване на точката.
6.33. Трептения на материална точка с маса T=0,1 g се получават съгласно уравнението х=А cos ω T,Където А=5 см; ω=20 s -1 . Определете максималните стойности на възстановяващата сила F max и кинетичната енергия T m ah.
6.34. Намерете възстановяваща сила Ев момента T=1 s и пълна енергия дматериална точка, осцилираща според закона х=А cos ω T, Където А = 20 см; ω=2π/3 s -1. Тегло Tматериалната точка е равна на 10 g.
6.35. Трептенията на материална точка възникват съгласно уравнението х=А cos ω T,Където А=8 cm, ω=π/6 s -1. В момента, когато възстановителната сила Еза първи път достигна стойност от -5 mN, потенциалната енергия P на точката стана равна на 100 μJ. Намерете този момент във времето Tи съответната му фаза ω T.
6.36. Претегляне на тегло м=250 g, окачен на пружина, трепти вертикално с период Т= 1с.Определете твърдостта кпружини.
6.37. Тежест беше окачена на спирална пружина, карайки пружината да се разтяга х=9вижте Какъв ще бъде периодът TОсцилира ли тежестта, ако я дръпнете малко надолу и след това я пуснете?
6.38. Тежест, окачена на пружина, се колебае вертикално с амплитуда А=4 см. Определете общата енергия двибрации на тежестта, ако твърдостта кпружината е 1 kN/m.
6.39. Намерете отношението на дължините на две математически махала, ако съотношението на техните периоди на трептене е 1,5.
6.40. l= 1м монтиран в асансьора. Асансьорът се издига с ускорение А=2,5 m/s 2. Определете период Tтрептения на махалото.
6.41. В краищата на тънка дължина на пръта л= 30 cm еднакви тежести са фиксирани, по една във всеки край. Пръчка с тежести се люлее около хоризонтална ос, минаваща през точка, разположена d=10 cm от единия край на пръта. Определете намалената дължина Ли точка Tтрептения на такова физическо махало. Пренебрегнете масата на пръта.
6.42. На дължина на пръта л=30 cm са закрепени две еднакви тежести: едната в средата на пръта, другата в единия му край. Прът с тежест се колебае около хоризонтална ос, минаваща през свободния край на пръта. Определете намалената дължина Ли точка Tвибрации на такава система. Пренебрегнете масата на пръта.
6.43. Система от три тежести, свързани с пръти с дължина л=30 cm (фиг. 6.6), се колебае около хоризонтална ос, минаваща през точка O, перпендикулярна на чертожната равнина. Намерете период Tсистемни вибрации. Пренебрегвайте масите на прътите; разглеждайте товарите като материални точки.
6.44. Тънък обръч, окачен на пирон, забит хоризонтално в стената, се колебае в равнина, успоредна на стената. Радиус Робръчът е 30 см. Изчислете периода Tвибрации на обръча.
 |
 |
| Ориз. 6.6 |
| Ориз. 6.7 |
6.45. Хомогенен диск с радиус Р=30 cm се колебае около хоризонтална ос, минаваща през една от образуващите на цилиндричната повърхност на диска. Какъв е периодът Tнеговото колебание?
6.46. Радиус на диска R= 24 cm се колебае около хоризонтална ос, минаваща през средата на един от радиусите, перпендикулярни на равнината на диска. Определете намалената дължина Ли точка Tтрептения на такова махало.
6.47. От тънък хомогенен диск с радиус Р= 20 см, изрязва се част, която прилича на кръг с радиус r= 10 cm, както е показано на фиг. 6.7. Останалата част от диска осцилира спрямо хоризонталната ос O, която съвпада с една от образуващите на цилиндричната повърхност на диска. Намерете период Tтрептения на такова махало.
6.48. Математическа дължина на махалото л 1 =40 cm и физическо махало под формата на тънък прав прът с дължина л 2 =60 cm трептят синхронно около една и съща хоризонтална ос. Определете разстоянието Ацентъра на масата на пръта от оста на вибрациите.
6.49. Физическо махало под формата на тънък прав прът с дължина л=120 cm се колебае около хоризонтална ос, минаваща перпендикулярно на пръта през точка на известно разстояние Аот центъра на масата на пръта. На каква стойност АПериод Tколебанията има най-малко значение?
6.50. Tс малка топка маса, прикрепена към него T.Махалото се колебае около хоризонтална ос, минаваща през точка О на пръта. Определете период Tхармонични трептения на махалото за случаи а, б, в, d показано на фиг. 6.8. Дължина лдължината на пръта е 1 м. Разгледайте топката като материална точка.
 |
 |
| Ориз. 6.9 |
| Ориз. 6.8 |
6.51. Физическото махало е тънък хомогенен прът с маса Tс две малки масови топки, прикрепени към него Tи 2 T. Махалото се колебае около хоризонтална ос, минаваща през точка ОТНОСНОна пръта. Определете честотата ν на хармоничните трептения на махалото за случаите a B C D,показано на фиг. 6.9. Дължина лдължината на пръта е 1 м. Разглеждайте топките като материални точки.
6.52. Телесна маса T=4 kg, фиксирана върху хоризонтална ос, осцилираща с период T 1 =0,8 s. Когато дискът е монтиран на тази ос, така че неговата ос съвпада с оста на вибрациите на тялото, периодът T 2 трептения станаха равни на 1,2 s. Радиус Рдискът е 20 см, масата му е равна на масата на тялото. Намерете инерционния момент Джтяло спрямо оста на вибрациите.
6.53. Масов хидрометър T=50 g, с диаметър на тръбата д= 1 см, плува във вода. Ареометърът беше леко потопен във вода и след това оставен на себе си, в резултат на което започна да извършва хармонични вибрации. Намерете период Tтези колебания.
6.54. В U-образна тръба, отворена в двата края, с площ на напречното сечение С=0,4 cm 2 бързо изсипете маса живак T=200 гр. Определете периода Tвибрации на живак в тръбата.
6.55. Издут дънер, чието напречно сечение е постоянно по цялата му дължина, се потапя вертикално във вода, така че само малка част (в сравнение с дължината му) да е над водата. Период Tвибрацията на трупа е 5 s. Определете дължината лтрупи
Затихващи трептения
6.56. Амплитуда на затихналите колебания на махалото във времето т 1=5 минути намалени наполовина. В колко време t2,като се брои от началния момент, амплитудата ще намалее осем пъти?
6.57. По време на T=8 min, амплитудата на затихналите трептения на махалото намалява три пъти. Определете коефициента на затихване δ .
6.58. Амплитудата на трептенията на махало с дължина l= 1 м на път T=10 минути намалени наполовина. Определете логаритмичния декремент на трептенията Θ.
6.59. Логаритмичният декремент на трептенията Θ на махалото е 0,003. Определете броя нобщите трептения, които махалото трябва да направи, за да се намали амплитудата наполовина.
6.60. Тегло маса T=500 g, окачени на спирална пружина с твърдост к=20 N/m и извършва еластични вибрации в определена среда. Логаритмичен декремент на трептенията Θ=0.004. Определете броя нпълните трептения, които тежестта трябва да направи, за да намалее амплитудата на трептенията н= 2 пъти. За колко дълго Tще има ли това намаление?
6.61. Телесна маса T=5 g извършва затихващи трептения. За време t= 50-те години тялото е загубило 60% от енергията си. Определете коефициента на съпротивление b.
6.62. Определете период Tзатихнали трептения, ако периодът Т 0собствените трептения на системата са равни на 1 s, а логаритмичният декремент на трептенията е Θ = 0,628.
6.64. Телесна маса T=1 kg е във вискозна среда с коефициент на съпротивление b=0,05 kg/s. Използване на две еднакви пружини на твърдост к=50 N/m всяко тяло се държи в равновесно положение, пружините не се деформират (фиг. 6.10). Тялото се измества от равновесното си положение и
освободен. Определете: 1) коефициента на затихване δ ; 2) честота ν на трептенията; 3) логаритмичен декремент на трептенията Θ; 4) номер нтрептения, след което амплитудата ще намалее с e пъти.
Принудителни вибрации. Резонанс
6.65. Под въздействието на гравитацията на електродвигателя, конзолната греда, върху която е монтиран, се огъва ч=1 мм. С каква скорост ПИма ли опасност от резонанс в арматурата на двигателя?
6.66. Тегло на колата T=80 t има четири извора. Твърдост кпружини на всяка пружина е 500 kN/m. При каква скорост колата ще започне да се люлее силно поради удари в релсите, ако дължината лрелсата е 12,8 м?
6.67. Осцилаторната система извършва затихващи трептения с честота ν=1000 Hz. Определете честотата ν 0 на собствените трептения, ако резонансната честота ν pe з =998 Hz.
6.68. Определете колко резонансната честота се различава от честотата ν 0 =l kHz на собствените трептения на системата, характеризираща се с коефициент на затихване δ=400 s -1 .
6.69. Определете логаритмичния декремент на трептенията Θ на трептящата система, за която се наблюдава резонанс при честота, по-ниска от собствената честота ν 0 =10 kHz с Δν=2 Hz.
6.70. Период T 0 собствени трептения на пружинно махало са равни на 0,55 s. Във вискозна среда периодът Tна същото махало стана равно на 0,56 s. Определете резонансната честота ν pe на трептенията.
6.71. Пружинно махало (твърдост кпружина е 10 N/m, маса Tнатоварване равно на 100 g) извършва принудителни вибрации във вискозна среда с коефициент на съпротивление r=2·10 -2 kg/s. Определете коефициента на затихване δ и резонансната амплитуда Арязане, ако стойността на амплитудата на движещата сила Е 0 =10 mN.
6.72. Тялото извършва принудителни трептения в среда с коефициент на съпротивление r= 1g/s. Приемайки, че затихването е малко, определете стойността на амплитудата на движещата сила, ако резонансната амплитуда А res =0,5 cm и честотата ν 0 на собствените трептения е 10 Hz.
6.73. Амплитудите на принудените хармонични трептения при честоти ν 1 =400 Hz и ν 2 =600 Hz са равни. Определете резонансната честота ν pe h. Пренебрегване на затихването.
6.74. За твърдост на винтовата пружина k= 10N/m окачена тежест от маса T=10 g и цялата система се потапя във вискозна среда. Вземане на коефициента на съпротивление bравна на 0,1 kg/s, определете: 1) честота ν 0 на собствените трептения; 2) резонансна честота ν pe з; 3) резонансна амплитуда Асрязване, ако движещата сила се променя по хармоничен закон и нейната амплитудна стойност F 0 ==0,02 N; 4) съотношението на резонансната амплитуда към статичното изместване под въздействието на сила F 0 .
6.75. Колко пъти амплитудата на принудените трептения ще бъде по-малка от резонансната амплитуда, ако честотата на промяна на движещата сила е по-голяма от резонансната честота: 1) с 10%? 2) два пъти? Коефициентът на затихване δ и в двата случая се приема равен на 0,1 ω 0 (ω 0 е ъгловата честота на естествените трептения).
Всяко периодично повтарящо се движение се нарича осцилаторно. Следователно зависимостите на координатите и скоростта на тялото от времето по време на трептения се описват с периодични функции на времето. В училищния курс по физика се разглеждат вибрации, при които зависимостите и скоростите на тялото са тригонометрични функции ![]() ,
, ![]() или комбинация от тях, където е определено число. Такива трептения се наричат хармонични (функции
или комбинация от тях, където е определено число. Такива трептения се наричат хармонични (функции ![]() И
И ![]() често наричани хармонични функции). За да решите задачи за трептения, включени в програмата на единния държавен изпит по физика, трябва да знаете дефинициите на основните характеристики на колебателното движение: амплитуда, период, честота, кръгова (или циклична) честота и фаза на трептенията. Нека дадем тези определения и да свържем изброените величини с параметрите на зависимостта на координатите на тялото от времето, които в случай на хармонични трептения винаги могат да бъдат представени във формата
често наричани хармонични функции). За да решите задачи за трептения, включени в програмата на единния държавен изпит по физика, трябва да знаете дефинициите на основните характеристики на колебателното движение: амплитуда, период, честота, кръгова (или циклична) честота и фаза на трептенията. Нека дадем тези определения и да свържем изброените величини с параметрите на зависимостта на координатите на тялото от времето, които в случай на хармонични трептения винаги могат да бъдат представени във формата
където , и са някои числа.
Амплитудата на трептенията е максималното отклонение на трептящо тяло от равновесното му положение. Тъй като максималните и минималните стойности на косинуса в (11.1) са равни на ±1, амплитудата на трептенията на осцилиращото тяло (11.1) е равна на . Периодът на трептене е минималното време, след което движението на тялото се повтаря. За зависимостта (11.1) периодът може да бъде зададен от следните съображения. Косинусът е периодична функция с период. Следователно движението се повтаря напълно през такава стойност, че . От тук получаваме
Кръговата (или цикличната) честота на трептенията е броят на трептенията, извършени за единица време. От формула (11.3) заключаваме, че кръговата честота е величината от формула (11.1).
Фазата на трептене е аргументът на тригонометрична функция, която описва зависимостта на координатата от времето. От формула (11.1) виждаме, че фазата на трептения на тялото, чието движение се описва от зависимостта (11.1), е равна на  . Стойността на фазата на трептене в момент = 0 се нарича начална фаза. За зависимост (11.1) началната фаза на трептенията е равна на . Очевидно началната фаза на трептенията зависи от избора на времевата отправна точка (момент = 0), която винаги е условна. Чрез промяна на произхода на времето началната фаза на трептенията винаги може да бъде „направена“ равна на нула, а синусът във формула (11.1) може да бъде „превърнат“ в косинус или обратно.
. Стойността на фазата на трептене в момент = 0 се нарича начална фаза. За зависимост (11.1) началната фаза на трептенията е равна на . Очевидно началната фаза на трептенията зависи от избора на времевата отправна точка (момент = 0), която винаги е условна. Чрез промяна на произхода на времето началната фаза на трептенията винаги може да бъде „направена“ равна на нула, а синусът във формула (11.1) може да бъде „превърнат“ в косинус или обратно.
 Програмата на единния държавен изпит включва и познаване на формули за честотата на трептения на пружинни и математически махала. Пружинно махало обикновено се нарича тяло, което може да се колебае върху гладка хоризонтална повърхност под действието на пружина, чийто втори край е фиксиран (лява фигура). Математическото махало е масивно тяло, чиито размери могат да бъдат пренебрегнати, което се люлее върху дълга, безтегловна и неразтеглива нишка (дясната фигура). Името на тази система е „ математическо махало“ се дължи на факта, че представлява абстракт математическимодел на истински ( физически) махало. Необходимо е да запомните формулите за периода (или честотата) на колебанията на пружинните и математическите махала. За пружинно махало
Програмата на единния държавен изпит включва и познаване на формули за честотата на трептения на пружинни и математически махала. Пружинно махало обикновено се нарича тяло, което може да се колебае върху гладка хоризонтална повърхност под действието на пружина, чийто втори край е фиксиран (лява фигура). Математическото махало е масивно тяло, чиито размери могат да бъдат пренебрегнати, което се люлее върху дълга, безтегловна и неразтеглива нишка (дясната фигура). Името на тази система е „ математическо махало“ се дължи на факта, че представлява абстракт математическимодел на истински ( физически) махало. Необходимо е да запомните формулите за периода (или честотата) на колебанията на пружинните и математическите махала. За пружинно махало
където е дължината на нишката, е ускорението на гравитацията. Нека разгледаме приложението на тези определения и закони, като използваме примера за решаване на проблеми.
За да се намери цикличната честота на трептенията на товара в задача 11.1.1Нека първо намерим периода на трептене и след това използваме формула (11.2). Тъй като 10 m 28 s е 628 s и през това време товарът се колебае 100 пъти, периодът на колебание на товара е 6,28 s. Следователно цикличната честота на трептенията е 1 s -1 (отговор 2 ). IN задача 11.1.2товарът направи 60 трептения за 600 s, така че честотата на трептене е 0,1 s -1 (отговор 1 ).
За да разберете разстоянието, което товарът ще измине за 2,5 периода ( задача 11.1.3), нека проследим движението му. След определен период товарът ще се върне обратно до точката на максимално отклонение, завършвайки пълно колебание. Следователно през това време товарът ще измине разстояние, равно на четири амплитуди: до равновесното положение - една амплитуда, от равновесното положение до точката на максимално отклонение в другата посока - втората, обратно до равновесното положение - трето, от равновесното положение до началната точка - четвъртото. През втория период натоварването отново ще премине през четири амплитуди, а през останалата половина от периода - две амплитуди. Следователно изминатото разстояние е равно на десет амплитуди (отговор 4 ).
Количеството движение на тялото е разстоянието от началната до крайната точка. Над 2,5 периода в задача 11.1.4тялото ще има време да извърши две пълни и половин пълно трептене, т.е. ще бъде при максимално отклонение, но от другата страна на равновесното положение. Следователно големината на изместването е равна на две амплитуди (отговор 3 ).
По дефиниция фазата на трептене е аргументът на тригонометрична функция, която описва зависимостта на координатите на трептящо тяло от времето. Следователно правилният отговор е задача 11.1.5 - 3 .
Периодът е времето на пълно трептене. Това означава, че връщането на тялото обратно в същата точка, от която тялото е започнало да се движи, не означава, че е изтекъл период: тялото трябва да се върне в същата точка със същата скорост. Например, тяло, започнало трептене от равновесно положение, ще има време да се отклони максимално в една посока, да се върне обратно, да се отклони максимално в другата посока и да се върне обратно. Следователно през периода тялото ще има време да се отклони максимално от равновесното положение два пъти и да се върне обратно. Следователно преминаването от равновесното положение до точката на максимално отклонение ( задача 11.1.6) тялото прекарва една четвърт от периода (отговор 3 ).
Хармоничните трептения са тези, при които зависимостта на координатите на трептящото тяло от времето се описва с тригонометрична (синус или косинус) функция на времето. IN задача 11.1.7това са функциите и въпреки факта, че включените в тях параметри са обозначени като 2 и 2 . Функцията е тригонометрична функция на квадрата на времето. Следователно вибрациите само на количества и са хармонични (отговор 4 ).
При хармонични трептения скоростта на тялото се изменя по закон  , където е амплитудата на колебанията на скоростта (референтната точка на времето е избрана така, че началната фаза на колебанията да е равна на нула). От тук намираме зависимостта на кинетичната енергия на тялото от времето
, където е амплитудата на колебанията на скоростта (референтната точка на времето е избрана така, че началната фаза на колебанията да е равна на нула). От тук намираме зависимостта на кинетичната енергия на тялото от времето  (задача 11.1.8). Използвайки по-нататък добре известната тригонометрична формула, получаваме
(задача 11.1.8). Използвайки по-нататък добре известната тригонометрична формула, получаваме
От тази формула следва, че кинетичната енергия на тялото се променя по време на хармонични трептения също по хармоничния закон, но с удвоена честота (отговор 2 ).
Зад връзката между кинетичната енергия на товара и потенциалната енергия на пружината ( задача 11.1.9) е лесно да се следва от следните съображения. Когато тялото се отклони максимално от равновесното положение, скоростта на тялото е нула и следователно потенциалната енергия на пружината е по-голяма от кинетичната енергия на товара. Напротив, когато тялото преминава през равновесното положение, потенциалната енергия на пружината е нула и следователно кинетичната енергия е по-голяма от потенциалната. Следователно, между преминаването на равновесното положение и максималното отклонение, кинетичната и потенциалната енергия се сравняват веднъж. И тъй като по време на период тялото преминава четири пъти от равновесното положение до максималното отклонение или обратно, тогава през периода кинетичната енергия на товара и потенциалната енергия на пружината се сравняват една с друга четири пъти (отговор 2 ).
Амплитуда на колебанията на скоростта ( задача 11.1.10) е най-лесно да се намери с помощта на закона за запазване на енергията. В точката на максимално отклонение енергията на осцилаторната система е равна на потенциалната енергия на пружината  , където е коефициентът на твърдост на пружината, е амплитудата на вибрациите. При преминаване през равновесното положение енергията на тялото е равна на кинетичната енергия
, където е коефициентът на твърдост на пружината, е амплитудата на вибрациите. При преминаване през равновесното положение енергията на тялото е равна на кинетичната енергия  , където е масата на тялото, е скоростта на тялото при преминаване през равновесното положение, която е максималната скорост на тялото по време на процеса на трептене и следователно представлява амплитудата на трептенията на скоростта. Приравнявайки тези енергии, намираме
, където е масата на тялото, е скоростта на тялото при преминаване през равновесното положение, която е максималната скорост на тялото по време на процеса на трептене и следователно представлява амплитудата на трептенията на скоростта. Приравнявайки тези енергии, намираме
(отговор 4 ).
От формула (11.5) заключаваме ( задача 11.2.2), че неговият период не зависи от масата на математическото махало и с увеличаване на дължината с 4 пъти, периодът на трептене се увеличава с 2 пъти (отговор 1 ).
Часовникът е осцилационен процес, който се използва за измерване на интервали от време ( задача 11.2.3). Думите „часовникът бърза“ означава, че периодът на този процес е по-малък от това, което трябва да бъде. Следователно, за да се изясни напредъкът на тези часовници, е необходимо да се увеличи периодът на процеса. Съгласно формула (11.5), за да се увеличи периодът на трептене на математическо махало, е необходимо да се увеличи дължината му (отговор 3 ).
За да намерите амплитудата на трептенията в задача 11.2.4, е необходимо да се представи зависимостта на координатите на тялото от времето под формата на една тригонометрична функция. За функцията, дадена в условието, това може да стане чрез въвеждане на допълнителен ъгъл. Умножаване и деление на тази функция на  и използвайки формулата за добавяне на тригонометрични функции, получаваме
и използвайки формулата за добавяне на тригонометрични функции, получаваме
|
къде е такъв ъгъл, че  . От тази формула следва, че амплитудата на трептенията на тялото е
. От тази формула следва, че амплитудата на трептенията на тялото е  (отговор 4
).
(отговор 4
).
>>Физика: Механични вибрации
Трептенията са много често срещан тип движение. Това е люлеенето на клоните на дърветата от вятъра, вибрациите на струните музикални инструменти, движението на буталото в цилиндъра на автомобилния двигател, люлеенето на махалото в стенния часовник и дори ударите на сърцето ни.
Темата на днешния урок ще бъде посветена на изучаването на трептенията и колебателните движения.
Процесът на трептене е най-често срещаният тип движение, който съществува в природата. И ако разгледаме този процес от гледна точка механични движения, тогава вибрациите могат да се нарекат най-често срещаният тип механично движение.
Концепцията за трептене се счита за движение, което се повтаря изцяло или частично във времето.
Смятате ли, че осцилаторните движения са люлеене на дървета или движение на листа под въздействието на вятъра? Естествено, такова движение може да се отдаде на трептения. Осцилаторните движения се извършват и от люлеещи се люлки, вибриращи струни на музикални инструменти и люлеене на махало в часовник. И дори всяко движение на човешкото тяло и сърдечния ни ритъм, което се повтаря във времето, също извършва колебателни движения.
Е, сега можем да направим заключение и да дефинираме това явление.
Процес, който се повтаря във времето, се нарича трептене.
Необходими условия за трептене
Сега нека разгледаме по-отблизо процеса на осцилаторни движения, като използваме примерите за пружинно и нишковидно махало.
Сега нека насочим вниманието си към нашите рисунки, които изобразяват тези махала.
На първата снимка ни е представено така нареченото нишковидно махало, което се нарича още математическо. Сега нека да видим какво представлява това математическо махало. И представлява някакво масивно тяло, в случая топка, която е окачена на дълга и тънка нишка. Ако се опитаме да я вземем и да я преместим настрани, нарушавайки равновесието й, и след това да я пуснем, тогава тази топка ще извършва многократни движения настрани, като в същото време периодично ще преминава през равновесното положение. В този случай можем да кажем, че тази топка ще започне да извършва осцилаторни движения, тоест да осцилира.
Сега разгледайте следната фигура, която показва пружинно махало. Това махало е представено под формата на тежест, която е прикрепена към пружина и под действието на еластичната сила на тази пружина е способна да извършва колебателни движения.
Но, както вече можете да видите от дадените примери, са необходими определени условия, за да възникнат колебания.
За да съществуват колебания е необходимо:
Първо, наличието на самата осцилаторна система. И в нашия случай такава система са тези махала, които са в състояние да извършват тези колебателни движения.
Второ, необходимо е да има точка на равновесие и освен това стабилно равновесие.
Трето, задължителното наличие на енергийни резерви, с помощта на които ще се извършват колебателни движения.
И, четвърто, наличието на малка сила на триене, тъй като ако силата на триене е голяма, тогава, естествено, не може да се говори за никакви вибрации.
Единици за амплитуда на вибрациите
Величините, които характеризират осцилаторните движения са:
1. Амплитуда, която се обозначава със символа „А“ и се измерва в единици за дължина като метри, сантиметри и др. По правило амплитудата се счита за максималното разстояние, на което тялото осцилира от равновесното си положение.
2. Периодът, който се обозначава със символа "Т" и се измерва в единици време, т.е. в минути, секунди и др. Периодът е времето, през което се извършва едно трептене.
3. Честота, която се обозначава със символа “V”. Честотата на трептене се счита за броя на трептенията, които се случват за 1 s.
В системата SI единицата за честота обикновено се нарича "херц". Името си получи в чест на немския физик Г. Херц.
Ако приемем, че честотата на трептене е равна на 1 Hz, това ще означава, че едно трептене се случва за една секунда. Ако честотата е v = 50 Hz, тогава естествено ще се появят 50 трептения в секунда.
Формули за амплитуда на трептене
Сега нека да преминем към разглеждане на вибрационните формули. Тук трябва да се отбележи, че за периода T и честотата v на трептенията, същите формули, които се използват за периода и честотата на въртене, ще бъдат правилни.
Нека разгледаме по-подробно значенията на тези формули:
1. Първо, за да намерим периода на трептене, трябва да вземем времето t, през което са направени определен брой трептения, и да го разделим на n, което е броят на тези трептения, и получаваме следната формула:
2. Второ, ако трябва да намерим честотата на трептенията, тогава трябва да вземем броя на трептенията и да ги разделим на времето, през което са възникнали тези трептения. В резултат на това получихме следната формула:
Но за да разберете по-добре как да преброите броя на вибрациите, трябва да имате представа какво представлява една пълна вибрация. За да направим това, нека отново се върнем към разглеждането на фиг. 30, където ясно се вижда, че махалото започва движението си от позиция 1, след това преминава през позицията на равновесие и се премества в позиция 2, след което се връща от втората позиция в позицията на равновесие и отново се връща в позиция 1. Това целият процес е с едно колебание.
Струва си да се обърне внимание на факта, че при сравняване на тези две формули периодът и честотата на трептенията са взаимно обратни величини, т.е.
Диаграма на колебанията
Както вече знаете от днешния урок, позицията на тялото по време на процеса на трептене непрекъснато се променя.
Графиката на трептене е графика на зависимост, където координатите на трептящо тяло зависят от времето.
Сега нека да разгледаме какво е флуктуационна графика. За да направим това, ще отделим време t по хоризонталната ос на нашата графика и ще поставим координатата x върху вертикалната ос. Сега, използвайки модула на тази координата, ние виждаме на какво разстояние от първоначалната позиция, тоест позицията на равновесие, се намира осцилиращото тяло в даден момент от времето.
И когато дадено тяло преминава през равновесното положение, тогава в този случай знакът на координатата се променя на противоположния. Тоест този знак ни показва, че тялото се е преместило от другата страна на равновесното положение.
Практическа работа
Сега нека направим малко интересни експерименти. За да направите това, нека се опитаме да свържем пружинно махало към пишещо устройство. И тогава ще започнем да движим равномерно хартиената лента пред това трептящо тяло. Ако погледнете внимателно Фигура 32, ще видите как на лентата се появява линия с помощта на четка, която ще съвпадне с графиката на трептенията.
Фигура 33 показва инсталирането на махало с низ, където трептенията на това махало също могат да бъдат записани. В този пример махалото е фуния, пълна с пясък. По същия начин поставяме хартиена лента под осцилираща фуния и наблюдаваме как пясъкът, който се изсипва от фунията, оставя съответна следа.

Сега виждаме, че на малки интервали и с доста ниско триене графиката на трептенията на тези махала е синусоида.

Така например на графиката можем да видим всички осцилаторни движения, където A = 5 cm, T = 4 s и v = 1/T = 0,25 Hz.
И вземете две безплатни уроци
В училище на английски SkyEng!
Самият аз уча там - много е готино. Има прогрес.
В приложението можете да научите думи, да тренирате слушане и произношение.
Пробвам. Два урока безплатно, използвайки моя линк!
Кликнете
Осцилаторни движения (или трептения)във физиката и технологията тези видове движения (или промени в състоянията) се наричат такива, които имат известна степен на повторяемост.
Трептенията, които възникват според законите на синуса или косинуса, се наричат хармонични.
Уравнение на хармоничните вибрации:
където t-време; x-стойност, променяща се с времето (координата, заряд, ток, емф и др.); А - амплитуда на трептенията - максималното отклонение на осцилиращата стойност от средната (нулева) стойност; - фаза на трептене; - начална фаза; w - циклична честота (промяна на фазата за единица време). През периода фазата се променя на .
Диференциално уравнение на хармоничните трептения
Уравнение от формата:
диференциално уравнение на хармоничните вибрации.
Видовете периодични трептения могат да бъдат представени с всякаква степен на точност като сума от хармонични трептения, така наречените хармонични серии.
Трептенията, които едно тяло ще направи, ако бъде извадено от равновесие (без значение как) и оставено само на себе си, се наричат свободни (собствени) трептения. Ако естествените вибрации са причинени от наличието само на квазиеластична сила, тогава те ще бъдат хармонични.
Вибрации на тялото, причинени от едновременното действие на квазиеластична сила и сила на триене (която е пропорционална на моментна скорост: ), се наричат затихнали трептения.
Уравнение (3) се нарича диференциално уравнение на затихващите трептения. Ето коефициента на затихване.
Решение на диференциалното уравнение на трептенията
Решението на диференциалното уравнение на затихналите трептения (3) е връзка от вида:
Уравнение (4) се нарича уравнение на затихналите трептения. Уравнение (4) показва, че амплитудата на затихналите трептения зависи от времето. Константите A се определят от началните условия. Амплитудата на трептенията намалява и те като цяло изглеждат както е показано на фиг. 1
 ориз. 1.
ориз. 1.
Периодът на затихналите трептения се изчислява по формула (5):
Физическото значение на коефициента на затихване е, че коефициентът на затихване е реципрочната стойност на времето за релаксация. А времето за релаксация е времето, през което амплитудата намалява с e пъти. Коефициентът на затихване обаче не характеризира напълно затихването. Обикновено затихването на трептенията се характеризира с декремент на затихване. Последният показва колко пъти намалява амплитудата на трептене за време, равно на периода на трептене. Тоест декрементът на затихване се определя, както следва:
Логаритъмът на декремента на затихване се нарича логаритмичен декремент, той очевидно е равен на:
Ако трептящата система е изложена на външна периодична сила, тогава възникват така наречените принудени трептения, които са незатихващи по природа.
Принудените трептения трябва да се разграничават от собствените трептения. В случай на автотрептения в системата се приема специален механизъм, който в такт със собствените си трептения „доставя” малки порции енергия на системата.
Примери за решаване на проблеми
ПРИМЕР 1
| Упражнение | Намерете енергия свободни вибрациитовар, окачен на пружина. Разгледайте случая на физическо махало, знаейки, че твърдостта на пружината е k, а амплитудата на трептенията е A.
|
| Решение | Нека намерим енергията на свободните вибрации. Представлява се от два вида енергия: кинетична и потенциална. За топка, окачена на пружина: Трептенията на топката се описват от уравнението на трептенията: Нека напишем уравнението за колебанията на скоростта на топката, като знаем, че движението се извършва само по оста X, следователно: Замествайки (1.2) и (1.3) в (1.1), получаваме: знаейки, че за физическо махало |
| Отговор | Енергията на свободните вибрации е пропорционална на квадрата на амплитудата на вибрациите |