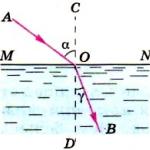
Тригонометрични уравнения- темата не е от най-простите. Те са твърде разнообразни.) Например тези:

sin 2 x + cos3x = ctg5x

sin(5x+π /4) = cot(2x-π /3)

sinx + cos2x + tg3x = ctg4x

и т.н...

Но тези (и всички други) тригонометрични чудовища имат две общи и задължителни характеристики. Първото - няма да повярвате - присъства в уравненията тригонометрични функции.) Второ: всички изрази с x са намерени в рамките на същите тези функции.И само там! Ако X се появи някъде навън,Например, sin2x + 3x = 3,това вече ще е уравнение от смесен тип. Такива уравнения изискват индивидуален подход. Няма да ги разглеждаме тук.

В този урок също няма да решаваме зли уравнения.) Тук ще се занимаваме с най-простите тригонометрични уравнения.Защо? Да, защото решението всякаквитригонометричните уравнения се състоят от два етапа. На първия етап злото уравнение се свежда до просто чрез различни трансформации. На втория се решава това най-просто уравнение. Няма друг начин.

Така че, ако имате проблеми на втория етап, първият етап няма много смисъл.)

Как изглеждат елементарните тригонометрични уравнения?

sinx = а

cosx = а

tgx = а

ctgx = a

Тук А означава произволно число. Всякакви.

Между другото, вътре в една функция може да няма чисто X, а някакъв вид израз, като:

cos(3x+π /3) = 1/2

и т.н. Това усложнява живота, но не засяга метода за решаване на тригонометрично уравнение.

Как се решават тригонометрични уравнения?

Тригонометричните уравнения могат да се решават по два начина. Първият начин: използване на логиката и тригонометричната окръжност. Ще разгледаме този път тук. Вторият начин - използване на памет и формули - ще бъде разгледан в следващия урок.

Първият начин е ясен, надежден и трудно се забравя.) Добър е за решаване на тригонометрични уравнения, неравенства и всякакви трудни нестандартни примери. Логиката е по-силна от паметта!)

Решаване на уравнения с помощта на тригонометрична окръжност.

Включваме елементарна логика и умение да използваме тригонометричния кръг. Не знаеш ли как? Въпреки това... Ще ви е трудно в тригонометрията...) Но това няма значение. Разгледайте уроците "Тригонометрична окръжност...... Какво е това?" и "Измерване на ъгли върху тригонометрична окръжност." Там всичко е просто. За разлика от учебниците...)

О, знаеш ли!? И дори усвои „Практическа работа с тригонометричния кръг“!? Честито. Тази тема ще ви бъде близка и разбираема.) Това, което е особено приятно е, че тригонометричен кръгняма значение какво уравнение решавате. Синус, косинус, тангенс, котангенс – всичко му е едно и също. Има само един принцип на решение.

Така че вземаме всяко елементарно тригонометрично уравнение. Поне това:

cosx = 0,5

Трябва да намерим X. Казано на човешки език, имате нужда намерете ъгъла (x), чийто косинус е 0,5.

Как използвахме кръга преди? Начертахме ъгъл върху него. В градуси или радиани. И то веднага трион тригонометрични функции на този ъгъл. Сега нека направим обратното. Нека начертаем косинус върху окръжността, равен на 0,5 и веднага ще видим ъгъл. Остава само да напиша отговора.) Да, да!

Начертайте кръг и маркирайте косинуса, равен на 0,5. По косинусовата ос, разбира се. Като този:

Сега нека начертаем ъгъла, който ни дава този косинус. Задръжте курсора на мишката върху снимката (или докоснете снимката на таблета) и ще видитеточно този ъгъл Х.

Косинусът на кой ъгъл е 0,5?

x = π /3

cos 60°= cos( π /3) = 0,5

Някои хора ще се засмят скептично, да... Например, струваше ли си да направим кръг, когато всичко вече е ясно... Можете, разбира се, да се смеете...) Но факт е, че това е грешен отговор. Или по-скоро недостатъчно. Познавачите на кръговете разбират, че тук има цял куп други ъгли, които също дават косинус от 0,5.

Ако завъртите подвижната страна OA пълен оборот, точка А ще се върне в първоначалната си позиция. Със същия косинус равен на 0,5. Тези. ъгълът ще се променис 360° или 2π радиана и косинус - не.Новият ъгъл 60° + 360° = 420° също ще бъде решение на нашето уравнение, т.к.

Могат да се правят такива пълни обороти безкрайно множество... И всички тези нови ъгли ще бъдат решения на нашето тригонометрично уравнение. И всички те трябва да бъдат записани по някакъв начин в отговор. Всичко.Иначе решението не се брои, да...)

Математиката може да направи това просто и елегантно. Запишете в един кратък отговор безкрайно множестворешения. Ето как изглежда нашето уравнение:

x = π /3 + 2π n, n ∈ Z

Ще го дешифрирам. Все пак пиши смисленоПо-приятно е, отколкото глупаво да рисувате мистериозни букви, нали?)

π /3 - това е същият ъгъл, който ние трионвърху кръга и определенспоред косинусовата таблица.

2π е една пълна революция в радиани.

н - това е броят на пълните, т.е. цялооб/мин Ясно е, че н може да бъде равно на 0, ±1, ±2, ±3.... и така нататък. Както е посочено от краткия запис:

n ∈ Z

н принадлежи ( ∈ ) набор от цели числа ( З ). Между другото, вместо писмото н буквите могат да бъдат използвани к, м, т и т.н.

Тази нотация означава, че можете да вземете всяко цяло число н . Най-малко -3, поне 0, поне +55. Каквото поискаш. Ако замените това число в отговора, ще получите конкретен ъгъл, който определено ще бъде решението на нашето сурово уравнение.)

Или, с други думи, x = π /3 е единственият корен на безкрайно множество. За да получите всички други корени, е достатъчно да добавите произволен брой пълни обороти към π /3 ( н ) в радиани. Тези. 2πn радиан.

Всичко? Не. Нарочно удължавам удоволствието. За да запомним по-добре.) Получихме само част от отговорите на нашето уравнение. Ще напиша тази първа част от решението така:

x 1 = π /3 + 2π n, n ∈ Z

х 1 - не само един корен, а цяла поредица от корени, записани в кратка форма.

Но има и ъгли, които също дават косинус от 0,5!

Да се ​​върнем към нашата снимка, от която записахме отговора. Ето я:

Задръжте мишката върху изображението и виждамедруг ъгъл, който също дава косинус от 0,5.На какво мислите, че е равно? Триъгълниците са еднакви... Да! То е равно на ъгъла х , само забавено в отрицателна посока. Това е ъгълът -Х. Но ние вече изчислихме x. π /3 или 60°. Следователно можем спокойно да напишем:

x 2 = - π /3

Е, разбира се, добавяме всички ъгли, които се получават чрез пълни обороти:

x 2 = - π /3 + 2π n, n ∈ Z

Това е всичко сега.) На тригонометричната окръжност ние трион(който разбира, разбира се)) всичкоъгли, които дават косинус от 0,5. И ние записахме тези ъгли в кратка математическа форма. Отговорът доведе до две безкрайни серии от корени:

x 1 = π /3 + 2π n, n ∈ Z

x 2 = - π /3 + 2π n, n ∈ Z

Това е правилният отговор.

надежда, общ принцип за решаване на тригонометрични уравненияизползването на кръг е ясно. Отбелязваме върху окръжност косинуса (синус, тангенс, котангенс) от даденото уравнение, начертаваме съответстващите му ъгли и записваме отговора.Разбира се, трябва да разберем какви ъгли сме трионвърху кръга. Понякога не е толкова очевидно. Е, казах, че тук е необходима логика.)

Например, нека разгледаме друго тригонометрично уравнение:

Моля, имайте предвид, че числото 0,5 не е единственото възможно число в уравненията!) Просто ми е по-удобно да го напиша, отколкото корени и дроби.

Ние работим според общия принцип. Начертаваме кръг, маркираме (на синусовата ос, разбира се!) 0,5. Начертаваме всички ъгли, съответстващи на този синус наведнъж. Получаваме тази снимка:

Нека първо се заемем с ъгъла х през първото тримесечие. Спомняме си таблицата на синусите и определяме стойността на този ъгъл. Това е проста работа:

x = π /6

Спомняме си за пълните завои и с чиста съвест записваме първата поредица от отговори:

x 1 = π /6 + 2π n, n ∈ Z

Половината работа е свършена. Но сега трябва да определим втори ъгъл...По-сложно е от косинусите, да... Но логиката ще ни спаси! Как да определим втория ъгъл през х? Да Лесно! Триъгълниците на снимката са еднакви, както и червеният ъгъл х равен на ъгъл х . Само той се брои от ъгъла π в отрицателна посока. Затова е червен.) А за отговора ни трябва ъгъл, измерен правилно от положителната полуос OX, т.е. от ъгъл 0 градуса.

Задръжте курсора върху чертежа и виждаме всичко. Премахнах първия ъгъл, за да не усложнявам картината. Ъгълът, който ни интересува (начертан в зелено), ще бъде равен на:

π - х

X ние знаем това π /6 . Следователно вторият ъгъл ще бъде:

π - π /6 = 5π /6

Отново си спомняме за добавянето на пълни обороти и записваме втората серия от отговори:

x 2 = 5π /6 + 2π n, n ∈ Z

Това е всичко. Пълният отговор се състои от две серии от корени:

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Тангенсните и котангенсните уравнения могат лесно да бъдат решени, като се използва същият общ принцип за решаване на тригонометрични уравнения. Ако, разбира се, знаете как да начертаете тангенс и котангенс върху тригонометрична окръжност.

В примерите по-горе използвах табличната стойност на синус и косинус: 0,5. Тези. едно от онези значения, които ученикът знае трябва да.Сега нека разширим възможностите си до всички други стойности.Решете, така че решете!)

И така, да кажем, че трябва да решим това тригонометрично уравнение:

В кратките таблици няма такава косинусова стойност. Хладно игнорираме този ужасен факт. Начертайте окръжност, маркирайте 2/3 върху косинусната ос и начертайте съответните ъгли. Получаваме тази снимка.

Нека да разгледаме първо ъгъла в първата четвърт. Само ако знаехме на какво е равно x, веднага щяхме да запишем отговора! Не знаем... Провал!? Спокоен! Математиката не оставя своя народ в беда! Тя измисли дъгови косинуси за този случай. Не знам? Напразно. Разберете, това е много по-лесно, отколкото си мислите. На този линк няма нито едно сложно заклинание за "обратни тригонометрични функции"... Това е излишно в тази тема.

Ако сте наясно, просто си кажете: "X е ъгъл, чийто косинус е равен на 2/3." И веднага, чисто по дефиницията на аркосинус, можем да напишем:

Спомняме си за допълнителните обороти и спокойно записваме първата серия от корени на нашето тригонометрично уравнение:

x 1 = arccos 2/3 + 2π n, n ∈ Z

Втората поредица от корени за втория ъгъл се записва почти автоматично. Всичко е същото, само X (arccos 2/3) ще бъде с минус:

x 2 = - arccos 2/3 + 2π n, n ∈ Z

И това е! Това е правилният отговор. Дори по-лесно, отколкото с таблични стойности. Няма нужда да помните нищо.) Между другото, най-внимателните ще забележат, че тази снимка показва решението през аркосинус по същество не се различава от картината за уравнението cosx = 0,5.

Точно! Общ принципЕто защо е често срещано! Нарочно нарисувах две почти еднакви картини. Кръгът ни показва ъгъла х по своя косинус. Дали е табличен косинус или не, не е известно на всички. Какъв вид ъгъл е това, π /3, или какво е арккосинус - това зависи от нас да решим.

Същата песен със синуса. Например:

Начертайте отново кръг, маркирайте синуса, равен на 1/3, начертайте ъглите. Това е картината, която получаваме:

И отново картината е почти същата като при уравнението sinx = 0,5.Отново започваме от корнер през първата четвърт. На какво е равно X, ако неговият синус е 1/3? Няма проблем!

Сега първият пакет корени е готов:

x 1 = arcsin 1/3 + 2π n, n ∈ Z

Нека се заемем с втория ъгъл. В примера с таблична стойност от 0,5 тя е равна на:

π - х

И тук ще бъде абсолютно същото! Само х е различно, arcsin 1/3. И какво от това!? Можете спокойно да запишете втория пакет корени:

x 2 = π - arcsin 1/3 + 2π n, n ∈ Z

Това е напълно правилен отговор. Въпреки че не изглежда много познато. Но е ясно, надявам се.)

Ето как тригонометричните уравнения се решават с помощта на кръг. Този път е ясен и разбираем. Той е този, който спестява в тригонометрични уравнения с избор на корени на даден интервал, в тригонометрични неравенства - те обикновено се решават почти винаги в кръг. Накратко, във всякакви задачи, които са малко по-трудни от стандартните.

Да приложим знанията на практика?)

Решете тригонометрични уравнения:

Първо, по-просто, направо от този урок.

Сега е по-сложно.

Съвет: тук ще трябва да помислите за кръга. Лично.)

И сега те са външно прости... Наричат ​​ги още специални случаи.

sinx = 0

sinx = 1

cosx = 0

cosx = -1

Подсказка: тук трябва да разберете в кръг къде има две серии от отговори и къде има една... И как да напишете една вместо две серии от отговори. Да, за да не се загуби нито един корен от безкраен брой!)

Е, много просто):

sinx = 0,3

cosx = π

tgx = 1,2

ctgx = 3,7

Съвет: тук трябва да знаете какво са арксинус и аркосинус? Какво е арктангенс, арккотангенс? Повечето прости определения. Но не е необходимо да помните стойности на таблица!)

Отговорите, разбира се, са бъркотия):

х 1= arcsin0,3 + 2π n, n ∈ Z
х 2= π - arcsin0,3 + 2

Не всичко се получава? Случва се. Прочетете урока отново. само замислено(има такава остаряла дума...) И следвайте връзките. Основните връзки са за кръга. Без нея тригонометрията е като пресичане на пътя със завързани очи. Понякога работи.)

Ако харесвате този сайт...

Между другото, имам още няколко интересни сайта за вас.)

Можете да практикувате решаване на примери и да разберете вашето ниво. Тестване с незабавна проверка. Да учим - с интерес!)

Можете да се запознаете с функции и производни.

Глава 15. Тригонометрични уравнения

15.6. Решаване на по-сложни тригонометрични уравнения

В предишните параграфи 3-5 са дадени решения на най-простите тригонометрични уравнения: , и . Към тях чрез идентични трансформации или решаване на помощна задача алгебрично уравнениепо-сложни тригонометрични уравнения, съдържащи няколко тригонометрични функции с еднакви или различни аргументи, се редуцират.

Общата техника за решаване на такива уравнения е да се заменят всички тригонометрични функции, включени в уравнението, с една функция въз основа на формули, свързващи тези функции. Когато решаваме уравнение, ние се стремим да правим трансформации, които водят до уравнения, еквивалентни на даденото. В противен случай трябва да проверите получените корени.

Загубата на корени е често срещана грешка. Други такива грешки са неточното познаване на формулите за решения на най-простите уравнения, както и невъзможността да се намери правилно търсената стойност на дъговата функция.

Нека да разгледаме примерите.

Решете уравнението.

Пример 2. (пример за редукция до един аргумент).

Решете уравнението.

Решение:
Препоръчително е да преминем към аргумента. Работата ни напомня за формулата за синус на двоен аргумент: .
Замествайки в уравнението, получаваме: .
От лявата страна отново ще приложим формулата за двоен аргумент синус, но първо ще умножим двете страни на уравнението по .
; ; .
Получихме най-простото уравнение от типа и приравняваме целия аргумент към решението на най-простото уравнение:
, където .

Решете уравнението.

Решение:
Използвайки една от формулите за намаляване на степента, получаваме .

След заместване в уравнението имаме

Решете уравнението.

Решение:
Прехвърляйки към дясната страна, получаваме, че е равно на:
; ; .
Тук трябваше да отидем чрез увеличаване на степента на уравнението, но получихме възможността да използваме добра техника за решаване - преместете всички членове в една част и разложете получения израз на множители:
.
Приравнявайки всеки фактор поотделно на нула, получаваме набор от уравнения,

което по правило е еквивалентно на това уравнение (изключение от това правило е разгледано в следващия пример).
Решаваме уравнението, имаме
, И .
Решаваме уравнението или , имаме и .

Решете уравнението.

Включване в отговор чужд коренсе счита за сериозна грешка. За да го избегнете, трябва да се уверите, че получените корени не превръщат в нула нито една от функциите в знаменателя на дробта на даденото уравнение (ако има дроби там) и че с тези корени никоя от функциите в оригиналното уравнение губи смисъл (ако е включено там). Трябва да запомните при какви стойности на аргумента функцията изчезва и областта на дефиниция на всяка тригонометрична функция.По аналогия те говорят за област на дефиниция на уравнение (домейнът на допустимите стойности или VA на неизвестното ). Областта на дефиниране на тригонометрично уравнение е обща част(пресечна точка) на областите на дефиниране на лявата и дясната страна на това уравнение. Ако полученият корен не принадлежи към областта на дефиниране на уравнението, тогава той е страничен и трябва да бъде изхвърлен.

Решете уравнението
.

Решение:
Да преминем към една функция. Ако го изразим чрез , получаваме ирационално уравнение, което е нежелателно. Замяна чрез:
; .
Нека решим полученото уравнение като квадратно уравнение по отношение на .
или .
Уравнението няма корени.
За уравнението имаме:
. Но те означават едно и също нечетни числа, така че нека напишем решението по-просто: .

Решете уравнението
.

За да получим хомогенно уравнение (всички членове от една и съща степен - втора) умножаваме дясната страна по израза, който е равен на .
;
.
Тъй като корените на уравнението не са корените на оригиналното уравнение (това може лесно да се провери чрез заместване), за да преминем към една функция, разделяме двете страни на уравнението на .

Нека решим квадратно уравнениеотносително .
или .
За уравнението имаме: .
За уравнението получаваме .

Решете уравнението.

Нека го изразим чрез и , получаваме
. Тук трябва да е различно от нула (в противен случай уравнението няма смисъл), така че областта на дефиниция на уравнението е всичко. Тъй като , ние умножаваме двете страни на уравнението по, за да се отървем от дробите.
;
;
.
За уравнението, което имаме

линия UMKГ. К. Муравина. Алгебра и начала математически анализ(10-11) (дълбоко)

Линия UMK G.K. Муравина, К.С. Муравина, О.В. Муравина. Алгебра и принципи на математическия анализ (10-11) (основен)

Как да преподаваме решаване на тригонометрични уравнения и неравенства: методи на обучение

Курсът по математика на Корпорацията за руски учебници, автори Георги Муравина и Олга Муравина, предвижда постепенен преход към решаване на тригонометрични уравнения и неравенства в 10 клас, както и продължаване на обучението им в 11 клас. Представяме на вашето внимание етапите на преход към темата с откъси от учебника „Алгебра и началото на математическия анализ“ (ниво за напреднали).

1. Синус и косинус на всеки ъгъл (пропедевтика за изучаване на тригонометрични уравнения)

Примерно задание.Намерете приблизително ъглите, чиито косинуси са равни на 0,8.

Решение.Косинусът е абсцисата на съответната точка от единичната окръжност. Всички точки с абсциса равна на 0,8 принадлежат на права линия, успоредна на ординатната ос и минаваща през т. ° С(0,8; 0). Тази права пресича единичната окръжност в две точки: П α ° И П β ° , симетричен спрямо абсцисната ос.

С помощта на транспортир намираме, че ъгълът α° приблизително равен на 37°. означава, обща формаъгли на завъртане с крайна точка П α°:

α° ≈ 37° + 360° н, Където н- произволно цяло число.

Поради симетрия спрямо абсцисната ос точката П β ° - крайна точка на завъртане под ъгъл –37°. Това означава, че за нея общата форма на ъглите на въртене е:

β° ≈ –37° + 360° н, Където н- произволно цяло число.

Отговор: 37° + 360° н, –37° + 360° н, Където н- произволно цяло число.

Примерно задание.Намерете ъглите, чиито синуси са равни на 0,5.

Решение.Синусът е ординатата на съответната точка от единичната окръжност. Всички точки с ординати равни на 0,5 принадлежат на права линия, успоредна на абсцисната ос и минаваща през т. д(0; 0,5).

Тази права пресича единичната окръжност в две точки: Пφ и Пπ–φ, симетричен спрямо ординатната ос. В правоъгълен триъгълник OKPφ крак КПφ е равно на половината от хипотенузата OPφ , означава,

Общ изглед на ъглите на завъртане с крайна точка П φ :

Където н- произволно цяло число. Общ изглед на ъглите на завъртане с крайна точка П π–φ :

Където н- произволно цяло число.

Отговор: Където н- произволно цяло число.

2. Тангенс и котангенс на всеки ъгъл (пропедевтика за изучаване на тригонометрични уравнения)

Пример 2.

Примерно задание.Намерете общия вид на ъгли, чийто тангенс е –1,2.

Решение.Нека отбележим точката на допирателната ос ° Сс ордината, равна на –1,2, и начертайте права линия O.C.. Направо O.C.пресича единичната окръжност в точки П α ° И Пβ° - краища със същия диаметър. Ъглите, съответстващи на тези точки, се различават един от друг с цял брой полуобороти, т.е. 180° н (н- цяло число). С помощта на транспортир намираме, че ъгълът П α° OP 0 е равно на –50°. Това означава, че общата форма на ъглите, чийто тангенс е –1,2 е както следва: –50° + 180° н (н- цяло число)

Отговор:–50° + 180° н, н∈ Z.

Използвайки синуса и косинуса на ъгли от 30°, 45° и 60°, е лесно да намерите техните тангенси и котангенси. Например,

Изброените ъгли са доста често срещани в различни задачи, така че е полезно да запомните стойностите на тангенса и котангенса на тези ъгли.

3. Най-простите тригонометрични уравнения

Въвеждат се следните обозначения: arcsin α, arccos α, arctg α, arcctg α. Не е препоръчително да бързате с въвеждането на комбинираната формула. Много по-удобно е да запишете две серии от корени, особено когато трябва да изберете корени на интервали.

Когато изучавате темата „най-простите тригонометрични уравнения“, уравненията най-често се свеждат до квадрати.

4. Формули за редукция

Формулите за редукция са идентичности, т.е. те са верни за всякакви валидни стойности φ . Анализирайки получената таблица, можете да видите, че:

1) знакът от дясната страна на формулата съвпада със знака на редуцируемата функция в съответния квадрант, ако вземем предвид φ остър ъгъл;

2) името се променя само от функциите на ъглите и

	φ + 2π н

5. Свойства и графика на функция y =грях х

Най-простите тригонометрични неравенства могат да се решават или върху графика, или върху окръжност. При решаване тригонометрично неравенствоПри кръг е важно да не объркате коя точка да посочите първо.

6. Свойства и графика на функция г=cos х

Задачата за изграждане на графика на функция г=cos хможе да се сведе до чертане на функцията y =грях х. Наистина, тъй като графика на функция г=cos хможе да се получи от графиката на функцията г= грях хизмествайки последната по оста x наляво с

7. Свойства и графики на функции г= tg хИ г=ctg х

Функционален домейн г= tg хвключва всички числа с изключение на числа от формата where н ∈ З. Както при конструирането на синусоида, първо ще се опитаме да получим графика на функцията г = tg хмежду

В левия край на този интервал тангентата е нула, а при приближаване до десния край стойностите на тангенса се увеличават неограничено. Графично изглежда като графика на функция г = tg хпритиска се към правата линия, вървейки нагоре с нея неограничено.

8. Зависимости между тригонометрични функции на един и същи аргумент

Равенството и изразяват отношения между тригонометрични функции на един и същ аргумент φ. С тяхна помощ, знаейки синуса и косинуса на определен ъгъл, можете да намерите неговия тангенс и котангенс. От тези равенства е лесно да се види, че тангенсът и котангенсът са свързани помежду си със следното равенство.

tg φ · легло φ = 1

Между тригонометричните функции има и други зависимости.

Уравнение на единичната окръжност с център в началото x 2 + y 2= 1 свързва абсцисата и ординатата на всяка точка от тази окръжност.

Фундаментално тригонометрично тъждество

cos 2 φ + sin 2 φ = 1

9. Синус и косинус от сбора и разликата на два ъгъла

Формула за сумата по косинус

cos (α + β) = cos α cos β – sin α sin β

Формула за косинус на разликата

cos (α – β) = cos α cos β + sin α sin β

Формула за синусова разлика

sin (α – β) = sin α cos β – cos α sin β

Формула за синусова сума

sin (α + β) = sin α cos β + cos α sin β

10. Тангенс на сбора и тангенс на разликата на два ъгъла

Формула за допирателна сума

Формула за допирателна разлика

Учебникът е включен в учебните материали по математика за 10–11 клас с изучаване на предмета начално ниво. Теоретичният материал е разделен на задължителен и избираем, системата от задачи е диференцирана по ниво на трудност, всяка глава завършва с тестови въпроси и задачи, а всяка глава с домашна работа тестова работа. Учебникът включва теми на проекти и връзки към Интернет ресурси.

11. Тригонометрични двойни ъглови функции

Формула за тангенс на двоен ъгъл

cos2α = 1 – 2sin 2 α cos2α = 2cos 2 α – 1

Примерно задание.Решете уравнението

Решение.

13. Решаване на тригонометрични уравнения

В повечето случаи първоначалното уравнение се свежда до прости тригонометрични уравнения по време на процеса на решаване. Въпреки това, няма единствен метод за решение на тригонометрични уравнения. Във всеки конкретен случай успехът зависи от знанията тригонометрични формулии способността да избирате правилните от тях. Въпреки това, изобилието от различни формули понякога прави този избор доста труден.

Уравнения, които се свеждат до квадрати

Примерно задание.Решете уравнение 2 cos 2 х+ 3 грях х = 0

Решение. С помощта на основния тригонометрична идентичносттова уравнение може да се сведе до квадратно уравнение по отношение на sin х:

2cos 2 х+3sin х= 0, 2(1 – грях 2 х) + 3sin х = 0,

2 – 2sin 2 х+3sin х= 0, 2sin 2 х– 3син х – 2 = 0

Нека въведем нова променлива г= грях х, тогава уравнението ще приеме формата: 2 г 2 – 3г – 2 = 0.

Корените на това уравнение г 1 = 2, г 2 = –0,5.

Връщане към променливата хи получаваме най-простите тригонометрични уравнения:

1) грях х= 2 – това уравнение няма корени, тъй като sin х < 2 при любом значении х;

2) грях х = –0,5,

Отговор:

Хомогенни тригонометрични уравнения

Примерно задание.Решете уравнението 2sin 2 х– 3син х cos х– 5cos 2 х = 0.

Решение.Нека разгледаме два случая:

1) cos х= 0 и 2) cos х ≠ 0.

Случай 1. Ако cos х= 0, тогава уравнението приема формата 2sin 2 х= 0, откъдето sin х= 0. Но това равенство не удовлетворява условието cos х= 0, тъй като при никакви обстоятелства хКосинус и синус не изчезват едновременно.

Случай 2. Ако cos х≠ 0, тогава можем да разделим уравнението на cos 2 x „Алгебра и началото на математическия анализ. 10 клас”, както и много други издания, е достъпно в платформата LECTA. За целта се възползвайте от офертата.

#ADVERTISING_INSERT#

В този урок ще разгледаме основни тригонометрични функции, техните свойства и графики, а също и списък основни видове тригонометрични уравнения и системи. Освен това посочваме общи решения на най-простите тригонометрични уравнения и техните частни случаи.

Този урок ще ви помогне да се подготвите за един от видовете задачи B5 и C1.

Подготовка за Единния държавен изпит по математика

Експериментирайте

Урок 10. Тригонометрични функции. Тригонометрични уравнения и техните системи.

Теория

Обобщение на урока

Вече сме използвали термина "тригонометрична функция" много пъти. В първия урок на тази тема ги идентифицирахме с помощта на правоъгълен триъгълники единични тригонометричен кръг. Използвайки тези методи за уточняване на тригонометрични функции, вече можем да заключим, че за тях една стойност на аргумента (или ъгъл) съответства на точно една стойност на функцията, т.е. имаме право да наричаме синус, косинус, тангенс и котангенс функции.

В този урок е време да се опитаме да се абстрахираме от обсъдените по-рано методи за изчисляване на стойностите на тригонометричните функции. Днес ще преминем към обичайния алгебричен подход за работа с функции, ще разгледаме техните свойства и ще изобразим графики.

По отношение на свойствата на тригонометричните функции трябва да се обърне специално внимание на:

Домейнът на дефиницията и обхватът на стойностите, т.к за синус и косинус има ограничения за обхвата на стойностите, а за тангенса и котангенса има ограничения за обхвата на определяне;

Периодичността на всички тригонометрични функции, т.к Вече отбелязахме наличието на най-малкия ненулев аргумент, добавянето на който не променя стойността на функцията. Този аргумент се нарича период на функцията и се означава с буквата . За синус/косинус и тангенс/котангенс тези периоди са различни.

Помислете за функцията:

1) Обхват на определението;

2) Диапазон на стойността ;

3) Функцията е нечетна ;

Нека изградим графика на функцията. В този случай е удобно да започнете конструкцията с изображение на областта, която ограничава графиката отгоре с числото 1 и отдолу с числото, което е свързано с диапазона от стойности на функцията. В допълнение, за изграждането е полезно да запомните стойностите на синусите на няколко основни ъгли на таблицата, например, че това ще ви позволи да изградите първата пълна „вълна“ на графиката и след това да я преначертаете надясно и наляво, като се възползва от факта, че картината ще се повтаря с отместване с точка, т.е. На .

Сега нека да разгледаме функцията:

Основните свойства на тази функция:

1) Обхват на определението;

2) Диапазон на стойността ;

3) Равномерна функция Това означава, че графиката на функцията е симетрична спрямо ординатата;

4) Функцията не е монотонна в цялата си област на дефиниране;

Нека изградим графика на функцията. Както при конструирането на синус, удобно е да започнете с изображение на областта, която ограничава графиката отгоре с числото 1 и отдолу с числото, което е свързано с диапазона от стойности на функцията. Ще начертаем и координатите на няколко точки на графиката, за които трябва да запомним стойностите на косинусите на няколко основни ъгли на таблицата, например, че с помощта на тези точки можем да изградим първата пълна „вълна ” на графиката и след това я преначертайте надясно и наляво, като се възползвате от факта, че картината ще се повтори с изместване на периода, т.е. На .

Да преминем към функцията:

Основните свойства на тази функция:

1) Домейн освен , където . Вече посочихме в предишни уроци, че не съществува. Това твърдение може да се обобщи чрез разглеждане на допирателния период;

2) Диапазон от стойности, т.е. допирателните стойности не са ограничени;

3) Функцията е нечетна ;

4) Функцията нараства монотонно в рамките на своите така наречени допирателни клонове, които сега ще видим на фигурата;

5) Функцията е периодична с период

Нека изградим графика на функцията. В този случай е удобно да започнете конструкцията, като изобразите вертикалните асимптоти на графиката в точки, които не са включени в дефиниционната област, т.е. и т.н. След това изобразяваме клоновете на допирателната вътре във всяка от лентите, образувани от асимптотите, като ги притискаме към лявата асимптота и към дясната. В същото време не забравяйте, че всеки клон се увеличава монотонно. Ние изобразяваме всички клони по същия начин, защото функцията има период равен на . Това се вижда от факта, че всеки клон се получава чрез изместване на съседния по абсцисната ос.

И завършваме с поглед към функцията:

Основните свойства на тази функция:

1) Домейн освен , където . От таблицата на стойностите на тригонометричните функции вече знаем, че не съществува. Това твърдение може да се обобщи, като се вземе предвид периодът на котангенса;

2) Диапазон от стойности, т.е. стойностите на котангенса не са ограничени;

3) Функцията е нечетна ;

4) Функцията намалява монотонно в своите клонове, които са подобни на допирателните клонове;

5) Функцията е периодична с период

Нека изградим графика на функцията. В този случай, що се отнася до допирателната, е удобно да започнете конструкцията, като изобразите вертикалните асимптоти на графиката в точки, които не са включени в областта на дефиницията, т.е. и т.н. След това изобразяваме клоновете на котангенса вътре във всяка от ивиците, образувани от асимптотите, като ги притискаме към лявата асимптота и към дясната. В този случай вземаме предвид, че всеки клон намалява монотонно. Ние изобразяваме всички клонове подобно на допирателната по същия начин, защото функцията има период равен на .

Отделно трябва да се отбележи, че тригонометричните функции със сложни аргументи могат да имат нестандартен период. Това е заотносно функциите на формата:

Периодът им е равен. А за функциите:

Периодът им е равен.

Както можете да видите, за да се изчисли нов период, стандартният период просто се разделя на коефициента в аргумента. Не зависи от други модификации на функцията.

Можете да разберете по-подробно и да разберете откъде идват тези формули в урока за конструиране и трансформиране на графики на функции.

Стигнахме до една от най-важните части на темата „Тригонометрия“, която ще посветим на решаването на тригонометрични уравнения. Способността за решаване на такива уравнения е важна, например, когато се описват колебателни процеси във физиката. Нека си представим, че сте карали няколко обиколки с картинг в спортна кола; решаването на тригонометрично уравнение ще ви помогне да определите колко време сте били в състезанието в зависимост от позицията на колата на пистата.

Нека напишем най-простото тригонометрично уравнение:

Решението на такова уравнение са аргументите, чийто синус е равен на . Но вече знаем, че поради периодичността на синуса има безкраен брой такива аргументи. Така решението на това уравнение ще бъде и т.н. Същото важи и за решаването на всяко друго просто тригонометрично уравнение, ще има безкраен брой.

Тригонометричните уравнения се делят на няколко основни типа. Отделно трябва да се спрем на най-простите, т.к всичко друго се свежда до тях. Има четири такива уравнения (според броя на основните тригонометрични функции). Общите решения за тях са известни, те трябва да се запомнят.

Най-простите тригонометрични уравнения и техните общи решенияизглежда така:

Моля, имайте предвид, че стойностите на синуса и косинуса трябва да вземат предвид ограниченията, които са ни известни. Ако, например, тогава уравнението няма решения и посочената формула не трябва да се прилага.

Освен това посочените коренни формули съдържат параметър под формата на произволно цяло число. IN училищна програмаТова е единственият случай, когато решението на уравнение без параметър съдържа параметър. Това произволно цяло число показва, че е възможно да се запишат безкраен брой корени на което и да е от горните уравнения просто чрез заместване на всички цели числа на свой ред.

С подробния извод на тези формули можете да се запознаете, като повторите глава „Тригонометрични уравнения” от програмата по алгебра за 10. клас.

Отделно е необходимо да се обърне внимание на решаването на специални случаи на най-простите уравнения със синус и косинус. Тези уравнения изглеждат така:

Към тях не трябва да се прилагат формули за намиране общи решения. Такива уравнения се решават най-удобно с помощта на тригонометричната окръжност, която дава по-прост резултат от общите формули за решение.

Например решението на уравнението е . Опитайте се сами да получите този отговор и решете останалите посочени уравнения.

В допълнение към посочения най-често срещан тип тригонометрични уравнения, има още няколко стандартни. Изброяваме ги, като вземаме предвид тези, които вече посочихме:

1) Протозои, Например, ;

2) Специални случаи на най-простите уравнения, Например, ;

3) Уравнения със сложен аргумент, Например, ;

4) Уравнения, намалени до най-простите им чрез изваждане на общ множител, Например, ;

5) Уравнения, редуцирани до техните най-прости чрез трансформиране на тригонометрични функции, Например, ;

6) Уравнения, редуцирани до най-простите им чрез заместване, Например, ;

7) Хомогенни уравнения , Например, ;

8) Уравнения, които могат да бъдат решени с помощта на свойствата на функциите, Например, . Не се тревожете от факта, че има две променливи в това уравнение; то се решава само;

Както и уравнения, които се решават с различни методи.

В допълнение към решаването на тригонометрични уравнения, трябва да можете да решавате техните системи.

Най-често срещаните видове системи са:

1) В което едно от уравненията е мощност, Например, ;

2) Системи от прости тригонометрични уравнения, Например, .

В днешния урок разгледахме основните тригонометрични функции, техните свойства и графики. Запознахме се и с общите формули за решаване на най-простите тригонометрични уравнения, посочихме основните видове такива уравнения и техните системи.

В практическата част на урока ще разгледаме методите за решаване на тригонометрични уравнения и техните системи.

Кутия 1.Решаване на частни случаи на най-простите тригонометрични уравнения.

Както вече казахме в основната част на урока, специални случаи на тригонометрични уравнения със синус и косинус от формата:

има повече прости решения, какво дават формулите за общи решения.

За това се използва тригонометричен кръг. Нека анализираме метода за решаването им, като използваме примера на уравнението.

Нека изобразим върху тригонометричната окръжност точката, в която стойността на косинуса е нула, което е и координатата по абсцисната ос. Както можете да видите, има две такива точки. Нашата задача е да посочим какво равен на ъгъла, което съответства на тези точки от окръжността.

Започваме да броим от положителната посока на абсцисната ос (косинусната ос) и при задаване на ъгъла стигаме до първата изобразена точка, т.е. едно решение би било тази стойност на ъгъла. Но все още сме доволни от ъгъла, който съответства на втората точка. Как да влезем в него?

Най-простите тригонометрични уравнения се решават, като правило, с помощта на формули. Нека ви напомня, че най-простите тригонометрични уравнения са:

sinx = а

cosx = а

tgx = а

ctgx = a

x е ъгълът, който трябва да се намери,
a е произволно число.

А ето и формулите, с които можете веднага да запишете решенията на тези най-прости уравнения.

За синус:

За косинус:

x = ± arccos a + 2π n, n ∈ Z

За допирателна:

x = arctan a + π n, n ∈ Z

За котангенс:

x = arcctg a + π n, n ∈ Z

Всъщност това е теоретичната част от решаването на най-простите тригонометрични уравнения. Освен това всичко!) Изобщо нищо. Въпреки това, броят на грешките по тази тема е просто извън класациите. Особено ако примерът леко се отклонява от шаблона. Защо?

Да, защото много хора пишат тези писма, без изобщо да разбират значението им!Пише предпазливо, да не би да стане нещо...) Това трябва да се изясни. Тригонометрия за хората или все пак хора за тригонометрията!?)

Да го разберем?

Един ъгъл ще бъде равен на arccos a, второ: -arccos a.

И винаги ще се получава по този начин.За всякакви А.

Ако не ми вярвате, задръжте курсора на мишката върху снимката или докоснете снимката на таблета си.) Промених номера А към нещо негативно. Както и да е, имаме един ъгъл arccos a, второ: -arccos a.

Следователно отговорът винаги може да бъде записан като две серии от корени:

x 1 = arccos a + 2π n, n ∈ Z

x 2 = - arccos a + 2π n, n ∈ Z

Нека комбинираме тези две серии в една:

x= ± arccos a + 2π n, n ∈ Z

И това е всичко. Получихме обща формула за решаване на най-простото тригонометрично уравнение с косинус.

Ако разбирате, че това не е някаква свръхнаучна мъдрост, а просто съкратена версия на две серии от отговори,Ще можете да се справите и със задачи „C“. С неравенства, с избиране на корени от даден интервал... Там отговорът с плюс/минус не работи. Но ако се отнасяте към отговора по делови начин и го разделите на два отделни отговора, всичко ще бъде разрешено.) Всъщност, затова го разглеждаме. Какво, как и къде.

В най-простото тригонометрично уравнение

sinx = а

ние също получаваме две серии от корени. Винаги. И тези две серии също могат да бъдат записани в един ред. Само този ред ще бъде по-сложен:

x = (-1) n arcsin a + π n, n ∈ Z

Но същността си остава същата. Математиците просто създадоха формула, за да направят един вместо два записа за поредица от корени. Това е всичко!

Да проверим математиците? И никога не се знае...)

В предишния урок беше обсъдено подробно решението (без никакви формули) на тригонометрично уравнение със синус:

Отговорът доведе до две серии от корени:

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Ако решим същото уравнение с помощта на формулата, получаваме отговора:

x = (-1) n arcsin 0,5 + π n, n ∈ Z

Всъщност това е недовършен отговор.) Ученикът трябва да знае това arcsin 0,5 = π /6.Пълният отговор би бил:

x = (-1)n π /6+ π n, n ∈ Z

Тук възниква интерес Питай. Отговорете чрез x 1; х 2 (това е верният отговор!) и чрез самотен х (и това е верният отговор!) - едно и също нещо ли са или не? Сега ще разберем.)

Заменяме в отговора с х 1 стойности н =0; 1; 2; и т.н., броим, получаваме поредица от корени:

x 1 = π/6; 13π/6; 25π/6 и така нататък.

Със същата замяна в отговор с х 2 , получаваме:

x 2 = 5π/6; 17π/6; 29π/6 и така нататък.

Сега нека заместим стойностите н (0; 1; 2; 3; 4...) в общата формула за единичен х . Тоест, повдигаме минус едно на нулева степен, след това на първа, втора и т.н. Е, разбира се, заместваме 0 във втория член; 1; 2 3; 4 и т.н. И ние броим. Получаваме серията:

x = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и така нататък.

Това е всичко, което можете да видите.) Обща формуладава ни абсолютно същите резултатикакто и двата отговора поотделно. Просто всичко наведнъж, подредено. Математиците не бяха заблудени.)

Могат да се проверят и формули за решаване на тригонометрични уравнения с тангенс и котангенс. Но ние няма.) Те вече са прости.

Изписах специално цялата тази замяна и проверка. Тук е важно да разберете едно просто нещо: има формули за решаване на елементарни тригонометрични уравнения, само, кратка бележкаотговори.За тази краткост трябваше да вмъкнем плюс/минус в решението за косинус и (-1) n в решението за синус.

Тези вложки не пречат по никакъв начин в задачи, в които просто трябва да запишете отговора на елементарно уравнение. Но ако трябва да разрешите неравенство или тогава трябва да направите нещо с отговора: изберете корени на интервал, проверете за ODZ и т.н., тези вмъквания могат лесно да обезпокоят човек.

И така, какво трябва да направя? Да, или напишете отговора в две серии, или решете уравнението/неравенството с помощта на тригонометричната окръжност. Тогава тези вмъквания изчезват и животът става по-лесен.)

Можем да обобщим.

За решаване на най-простите тригонометрични уравнения има готови формули за отговор. Четири броя. Те са добри за незабавно записване на решението на уравнение. Например, трябва да решите уравненията:

sinx = 0,3

Лесно: x = (-1) n arcsin 0,3 + π n, n ∈ Z

cosx = 0,2

Няма проблем: x = ± arccos 0,2 + 2π n, n ∈ Z

tgx = 1,2

Лесно: x = arctan 1,2 + π n, n ∈ Z

ctgx = 3,7

Остава един: x= arcctg3,7 + π n, n ∈ Z

cos x = 1,8

Ако вие, блестящи със знания, незабавно напишете отговора:

x= ± arccos 1,8 + 2π n, n ∈ Z

тогава вече светиш, това... онова... от локва.) Верен отговор: няма решения. не разбирам защо? Прочетете какво е аркосинус. Освен това, ако от дясната страна на оригиналното уравнение има таблични стойности на синус, косинус, тангенс, котангенс, - 1; 0; √3; 1/2; √3/2 и така нататък. - отговорът през арките ще бъде недовършен. Арките трябва да бъдат преобразувани в радиани.

И ако срещнете неравенство, например

тогава отговорът е:

x πn, n ∈ Z

има редки глупости, да...) Тук трябва да решите с помощта на тригонометричната окръжност. Какво ще правим в съответната тема.

За тези, които героично четат тези редове. Просто не мога да не оценя титаничните ви усилия. Бонус за вас.)

Бонус:

Когато записват формули в тревожна бойна ситуация, дори опитни маниаци често се объркват къде πn, И къде 2π n. Ето един лесен трик за вас. в всекиформули на стойност πn. С изключение на единствената формула с аркосинус. Стои там 2πn. двепеен. Ключова дума - две.В същата тази формула има двезнак в началото. Плюс и минус. Тук-там - две.

Така че, ако сте писали двезнак преди аркокосинуса, по-лесно е да запомните какво ще се случи накрая двепеен. И това се случва и обратното. Човекът ще пропусне знака ± , стига до края, пише правилно две Pien, и той ще дойде на себе си. Има нещо напред двезнак! Човекът ще се върне в началото и ще поправи грешката! Като този.)

Ако харесвате този сайт...

Между другото, имам още няколко интересни сайта за вас.)

Можете да практикувате решаване на примери и да разберете вашето ниво. Тестване с незабавна проверка. Да учим - с интерес!)

Можете да се запознаете с функции и производни.