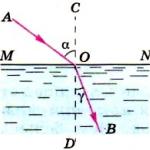
Тригонометрични уравнения .

Най-простите тригонометрични уравнения .

Методи за решаване на тригонометрични уравнения.

Тригонометрични уравнения. Уравнение, съдържащо неизвестно под знакът на тригонометричната функция се нарича тригонометричен.

Най-простите тригонометрични уравнения.

Методи за решаване на тригонометрични уравнения. Решаването на тригонометрично уравнение се състои от два етапа: трансформация на уравнениеза да стане най-простотип (виж по-горе) и решениеполучената най-проста тригонометрично уравнение.Има седем основни методи за решаване на тригонометрични уравнения.

1. Алгебричен метод. Този метод ни е добре познат от алгебрата.

(променлива замяна и метод на заместване).

2. Разлагане на множители. Нека да разгледаме този метод с примери.

Пример 1. Решете уравнението:грях х+cos х = 1 .

Решение Нека преместим всички членове на уравнението вляво:

грях х+cos х – 1 = 0 ,

Нека трансформираме и разложим израза на множители

Лявата страна на уравнението:

Пример 2. Решете уравнението: cos 2 х+ грях х cos х = 1.

Решение: cos 2 х+ грях х cos х– грях 2 х– cos 2 х = 0 ,

грях х cos х– грях 2 х = 0 ,

грях х· (cos х– грях х ) = 0 ,

Пример 3. Решете уравнението:защото 2 х– защото 8 х+ cos 6 х = 1.

Решение: cos 2 х+ cos 6 х= 1 + cos 8 х,

2 cos 4 хзащото 2 х= 2cos² 4 х ,

Cos 4 х · (cos 2 х– cos 4 х) = 0 ,

Cos 4 х · 2 грях 3 хгрях х = 0 ,

1). защото 4 х= 0, 2). грях 3 х= 0, 3). грях х = 0 ,

3.

Водещо до хомогенно уравнение. Уравнението Наречен хомогенен от относно гряхИ cos , Ако всичко това термини от същата степен спрямо гряхИ cosсъщия ъгъл. За да решите хомогенно уравнение, трябва: А) преместете всичките си членове вляво; b) извадете всички общи множители извън скоби; V) приравнява всички множители и скоби към нула; Ж) скоби, равни на нула, дават хомогенно уравнение от по-малка степен, което трябва да се раздели на cos(или грях) в старша степен; д) реши полученото алгебрично уравнение по отношение натен . ПРИМЕР Решете уравнение: 3грях 2 х+ 4 грях х cos х+ 5cos 2 х = 2. Решение: 3sin 2 х+ 4 грях х cos х+ 5 cos 2 х= 2sin 2 х+ 2cos 2 х , грях 2 х+ 4 грях х cos х+ 3, защото 2 х = 0 , тен 2 х+ 4 тен х + 3 = 0 , оттук г 2 + 4г +3 = 0 , Корените на това уравнение са:г 1 = - 1, г 2 = - 3, следователно 1) тен х= –1, 2) тен х = –3,

4. Преход към полуъгъл. Нека разгледаме този метод като пример:

ПРИМЕР Решете уравнение: 3грях х– 5 cos х = 7.

Решение: 6 грях ( х/ 2) cos ( х/ 2) – 5 cos² ( х/ 2) + 5 sin² ( х/ 2) =

7 sin² ( х/ 2) + 7 cos² ( х/ 2) ,

2 sin² ( х/ 2) – 6 грях ( х/ 2) cos ( х/ 2) + 12 cos² ( х/ 2) = 0 ,

тен² ( х/ 2) – 3 тен ( х/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Въвеждане на спомагателен ъгъл. Разгледайте уравнение на формата:

агрях х + b cos х = ° С ,

Където а, b, ° С– коефициенти;х– неизвестен.

Сега коефициентите на уравнението имат свойствата на синус и косинус, именно: модул (абсолютна стойност) на всеки

Примери:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

Как се решават тригонометрични уравнения:

Всяко тригонометрично уравнение трябва да бъде сведено до един от следните типове:

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

където \(t\) е израз с x, \(a\) е число. Такива тригонометрични уравненияса наречени най-простият. Те могат лесно да бъдат решени с помощта на () или специални формули:

Вижте инфографики за решаване на прости тригонометрични уравнения тук: и.

Пример . Решете тригонометричното уравнение \(\sin⁡x=-\)\(\frac(1)(2)\).
Решение:

Отговор: \(\left[ \begin(gathered)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \end(gathered)\right.\) \(k,n∈Z\)

Какво означава всеки символ във формулата за корените на тригонометричните уравнения, вижте.

внимание!Уравненията \(\sin⁡x=a\) и \(\cos⁡x=a\) нямат решения, ако \(a ϵ (-∞;-1)∪(1;∞)\). Тъй като синус и косинус за всеки x са по-големи или равни на \(-1\) и по-малки или равни на \(1\):

\(-1≤\sin x≤1\) \(-1≤\cos⁡x≤1\)

Пример . Решете уравнението \(\cos⁡x=-1,1\).
Решение: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Отговор : няма решения.

Пример . Решете тригонометричното уравнение tg\(⁡x=1\).
Решение:

Нека решим уравнението с помощта на числовата окръжност. За това: 1) Конструирайте кръг) 2) Построете осите \(x\) и \(y\) и допирателната ос (тя минава през точката \((0;1)\), успоредна на оста \(y\)). 3) На допирателната ос маркирайте точката \(1\). 4) Свържете тази точка и началото на координатите - права линия. 5) Отбележете пресечните точки на тази права и числовата окръжност. 6) Нека подпишем стойностите на тези точки: \(\frac(π)(4)\) ,\(\frac(5π)(4)\) 7) Запишете всички стойности на тези точки. Тъй като те са разположени на разстояние точно \(π\) една от друга, всички стойности могат да бъдат записани в една формула:

Отговор: \(x=\)\(\frac(π)(4)\) \(+πk\), \(k∈Z\).

Пример . Решете тригонометричното уравнение \(\cos⁡(3x+\frac(π)(4))=0\).
Решение:

Нека отново използваме числовия кръг. 1) Построете окръжност, оси \(x\) и \(y\). 2) На косинусовата ос (\(x\) ос) маркирайте \(0\). 3) Начертайте перпендикуляр на косинусовата ос през тази точка. 4) Маркирайте пресечните точки на перпендикуляра и окръжността. 5) Нека подпишем стойностите на тези точки: \(-\) \(\frac(π)(2)\),\(\frac(π)(2)\). 6) Записваме цялата стойност на тези точки и ги приравняваме към косинуса (към това, което е вътре в косинуса). \(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\) \(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\) 8) Както обикновено, ще изразим \(x\) в уравнения. Не забравяйте да третирате числата с \(π\), както и с \(1\), \(2\), \(\frac(1)(4)\) и т.н. Това са същите числа като всички останали. Без цифрова дискриминация! \(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=\)\(\frac(π)(4)\) \(+2πk\) \(|:3\) \(3x=-\)\(\frac(3π)(4)\) \(+2πk\) \(|:3\) \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\)

Отговор: \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\) , \(k∈Z\).

Намаляването на тригонометричните уравнения до най-простите е творческа задача; тук трябва да използвате и двете, и специални методи за решаване на уравнения:
- Метод (най-популярният в Единния държавен изпит).
- Метод.
- Метод на спомагателните аргументи.

Нека разгледаме пример за решаване на квадратно тригонометрично уравнение

Пример . Решете тригонометричното уравнение \(2\cos^2⁡x-5\cos⁡x+2=0\)
Решение:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	Нека направим замяната \(t=\cos⁡x\).
	Нашето уравнение стана типично. Можете да го разрешите с помощта на.
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	Правим обратна замяна.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	Решаваме първото уравнение с помощта на числовата окръжност. Второто уравнение няма решения, защото \(\cos⁡x∈[-1;1]\) и не може да бъде равно на две за всяко x.
	Нека напишем всички числа, лежащи в тези точки.

Отговор: \(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\).

Пример за решаване на тригонометрично уравнение с изследване на ODZ:

Пример (USE) . Решете тригонометричното уравнение \(=0\)

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Има дроб и има котангенс - това означава, че трябва да го запишем. Нека ви напомня, че котангенсът всъщност е дроб: ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) Следователно ODZ за ctg\(x\): \(\sin⁡x≠0\).
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\)	Нека отбележим „нерешенията“ върху числовата окръжност.
\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Нека се отървем от знаменателя в уравнението, като го умножим по ctg\(x\). Можем да направим това, тъй като по-горе написахме, че ctg\(x ≠0\).
\(2\cos^2⁡x-\sin⁡(2x)=0\)	Нека приложим формулата за двоен ъгъл за синус: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	Ако ръцете ви се протегнат да делите на косинус, дръпнете ги назад! Можете да разделите на израз с променлива, ако тя определено не е равна на нула (например тези: \(x^2+1.5^x\)). Вместо това нека извадим \(\cos⁡x\) извън скоби.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	Нека "разделим" уравнението на две.
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	Нека решим първото уравнение с помощта на числовата окръжност. Нека разделим второто уравнение на \(2\) и преместим \(\sin⁡x\) в дясната страна.
\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	Получените корени не се включват в ОДЗ. Затова няма да ги запишем в отговор. Второто уравнение е типично. Нека го разделим на \(\sin⁡x\) (\(\sin⁡x=0\) не може да бъде решение на уравнението, защото в този случай \(\cos⁡x=1\) или \(\cos⁡ x=-1\)).
	Отново използваме кръг.
\(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\)	Тези корени не са изключени от ODZ, така че можете да ги напишете в отговора.

Отговор: \(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\).

Концепция за решаване на тригонометрични уравнения.

• За да решите тригонометрично уравнение, преобразувайте го в едно или повече основни тригонометрични уравнения. Решаването на тригонометрично уравнение в крайна сметка се свежда до решаването на четирите основни тригонометрични уравнения.

Решаване на основни тригонометрични уравнения.

• Има 4 вида основни тригонометрични уравнения:
• sin x = a; cos x = a
• тен х = а; ctg x = a
• Решаването на основни тригонометрични уравнения включва разглеждане на различни позиции x върху единичната окръжност, както и използване на таблица за преобразуване (или калкулатор).
• Пример 1. sin x = 0,866. С помощта на таблица за преобразуване (или калкулатор) ще получите отговора: x = π/3. Единичната окръжност дава друг отговор: 2π/3. Запомнете: всички тригонометрични функции са периодични, което означава, че техните стойности се повтарят. Например, периодичността на sin x и cos x е 2πn, а периодичността на tg x и ctg x е πn. Следователно отговорът е написан по следния начин:
• x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
• Пример 2. cos x = -1/2. С помощта на таблица за преобразуване (или калкулатор) ще получите отговора: x = 2π/3. Единичната окръжност дава друг отговор: -2π/3.
• x1 = 2π/3 + 2π; x2 = -2π/3 + 2π.
• Пример 3. tg (x - π/4) = 0.
• Отговор: x = π/4 + πn.
• Пример 4. ctg 2x = 1,732.
• Отговор: x = π/12 + πn.

Трансформации, използвани при решаване на тригонометрични уравнения.

• За преобразуване на тригонометрични уравнения се използват алгебрични трансформации (факторизация, редукция на хомогенни членове и др.) и тригонометрични тъждества.
• Пример 5: Използвайки тригонометрични идентичности, уравнението sin x + sin 2x + sin 3x = 0 се преобразува в уравнението 4cos x*sin (3x/2)*cos (x/2) = 0. По този начин следните основни тригонометрични уравнения трябва да се реши: cos x = 0; sin(3x/2) = 0; cos(x/2) = 0.

• Намиране на ъгли с помощта на известни стойности на функцията.

  • Преди да научите как да решавате тригонометрични уравнения, трябва да научите как да намирате ъгли, като използвате известни стойности на функцията. Това може да стане с помощта на таблица за преобразуване или калкулатор.
  • Пример: cos x = 0,732. Калкулаторът ще даде отговора x = 42,95 градуса. Единичната окръжност ще даде допълнителни ъгли, чийто косинус също е 0,732.

• Отделете разтвора върху единичната окръжност.

  • Можете да начертаете решения на тригонометрично уравнение върху единичната окръжност. Решения на тригонометрично уравнение върху единичната окръжност са върховете на правилен многоъгълник.
  • Пример: Решенията x = π/3 + πn/2 върху единичната окръжност представляват върховете на квадрата.
  • Пример: Решенията x = π/4 + πn/3 върху единичната окръжност представляват върховете на правилен шестоъгълник.

• Методи за решаване на тригонометрични уравнения.

  • Ако дадено тригонометрично уравнение съдържа само една тригонометрична функция, решете това уравнение като основно тригонометрично уравнение. Ако дадено уравнение включва две или повече тригонометрични функции, тогава има 2 метода за решаване на такова уравнение (в зависимост от възможността за неговото преобразуване).
    • Метод 1.
  • Преобразувайте това уравнение в уравнение от вида: f(x)*g(x)*h(x) = 0, където f(x), g(x), h(x) са основните тригонометрични уравнения.
  • Пример 6. 2cos x + sin 2x = 0. (0< x < 2π)
  • Решение. Като използвате формулата за двоен ъгъл sin 2x = 2*sin x*cos x, заменете sin 2x.
  • 2cos x + 2*sin x*cos x = 2cos x*(sin x + 1) = 0. Сега решете двете основни тригонометрични уравнения: cos x = 0 и (sin x + 1) = 0.
  • Пример 7. cos x + cos 2x + cos 3x = 0. (0< x < 2π)
  • Решение: Използвайки тригонометрични идентичности, преобразувайте това уравнение в уравнение от вида: cos 2x(2cos x + 1) = 0. Сега решете двете основни тригонометрични уравнения: cos 2x = 0 и (2cos x + 1) = 0.
  • Пример 8. sin x - sin 3x = cos 2x. (0< x < 2π)
  • Решение: Използвайки тригонометрични идентичности, преобразувайте това уравнение в уравнение от вида: -cos 2x*(2sin x + 1) = 0. Сега решете двете основни тригонометрични уравнения: cos 2x = 0 и (2sin x + 1) = 0 .
    • Метод 2.
  • Преобразувайте даденото тригонометрично уравнение в уравнение, съдържащо само една тригонометрична функция. След това заменете тази тригонометрична функция с някаква неизвестна, например t (sin x = t; cos x = t; cos 2x = t, tan x = t; tg (x/2) = t и т.н.).
  • Пример 9. 3sin^2 x - 2cos^2 x = 4sin x + 7 (0< x < 2π).
  • Решение. В това уравнение заменете (cos^2 x) с (1 - sin^2 x) (според тъждеството). Трансформираното уравнение е:
  • 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Заменете sin x с t. Сега уравнението е: 5t^2 - 4t - 9 = 0. Това е квадратно уравнение, имащ два корена: t1 = -1 и t2 = 9/5. Вторият корен t2 не отговаря на обхвата на функцията (-1< sin x < 1). Теперь решите: t = sin х = -1; х = 3π/2.
  • Пример 10. tg x + 2 tg^2 x = ctg x + 2
  • Решение. Заменете tg x с t. Пренапишете оригиналното уравнение, както следва: (2t + 1)(t^2 - 1) = 0. Сега намерете t и след това намерете x за t = tan x.

• Специални тригонометрични уравнения.

  • Има няколко специални тригонометрични уравнения, които изискват специфични трансформации. Примери:
  • a*sin x+ b*cos x = c; a(sin x + cos x) + b*cos x*sin x = c;
  • a*sin^2 x + b*sin x*cos x + c*cos^2 x = 0

• Периодичност тригонометрични функции.

  • Както бе споменато по-рано, всички тригонометрични функции са периодични, което означава, че техните стойности се повтарят след определен период. Примери:
    • Периодът на функцията f(x) = sin x е 2π.
    • Периодът на функцията f(x) = tan x е равен на π.
    • Периодът на функцията f(x) = sin 2x е равен на π.
    • Периодът на функцията f(x) = cos (x/2) е 4π.
  • Ако в проблема е указан период, изчислете стойността на "x" в рамките на този период.
  • Забележка: Решаването на тригонометрични уравнения не е лесна задача и често води до грешки. Затова проверете внимателно отговорите си. За да направите това, можете да използвате графичен калкулатор, за да начертаете даденото уравнение R(x) = 0. В такива случаи решенията ще бъдат представени като десетични знаци (т.е. π се заменя с 3,14).

Тригонометрични уравнения

Решаване на прости тригонометрични уравнения

Градуси и радиани

Въведение в тригонометричния кръг

Завъртания върху тригонометрична окръжност

Има толкова много болка, свързана с думата тригонометрия. Тази тема се появява в 9 клас и никога не изчезва. Трудно е за тези, които не разбират нещо веднага. Нека се опитаме да поправим това, за да озарим лицето ви с усмивка, когато чуете думата тригонометрия, или поне да постигнем „лице на покер“.

Нека започнем с факта, че точно както дължината може да бъде изразена в метри или мили, така е ъгълът може да бъде изразен в радиани или градуси.

1 радиан = 180/π ≈ 57,3 градуса

Но е по-лесно да запомните цели числа: 3,14 радиана = 180 градуса.Това е една и съща стойност на числото π.

Нека си припомним, че ако ни помолят да се обърнем, тогава трябва да се обърнем на 180 градуса, а сега можем също да кажем: Обърни π!

Ще говорим за графики на синус, косинус и танге в друга статия.

Сега нека започнем с декартовата (правоъгълна) координатна система.

Преди това тя помагаше в изграждането на графики, а сега ще помогне със синус и косинус.

В пресечната точка на оста X и оста Y изграждаме единична окръжност (радиус равен на 1):

Тогава Косинусовата ос ще съвпадне с x, синусовата ос с y. Тангенсната и котангенсната ос също са показани на фигурата.

Сега нека отбележим основните стойности на градуси и радиани върху кръг.

Нека да Нека се съгласим с вас като възрастни:върху кръга ще отбележим ъгъла в радиани, тоест през Pi.

Достатъчно е да запомните, че π = 180°(тогава π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

А сега да се завъртим в кръг! Обичайно е да се вземе крайната дясна точка на кръга (където 0°) като начало на доклада:

Оттам завиваме още един завой. Можем да се въртим както в положителна посока (обратно на часовниковата стрелка), така и в отрицателна посока (по часовниковата стрелка).

Има два начина за завъртане на 45°: над лявото рамо 45° на (+) страна или над дясното рамо на 315° на (-) страна.

Основното нещо е посоката, в която ще гледаме, а не ъгълът!

Трябва да насочим пунктираната линия към 100 точки, но няма значение колко оборота правим около себе си и в каква посока!

Можете да получите 100 точки, като завъртите 135° или 360°+135°, или -225°, или -225°-360°...

И сега имате две възможности:

Научете целия кръг (тригонометър). Не е лош вариант, ако паметта ви е отлична и нищо няма да ви се изплъзне от главата в решаващ момент:

Или можете да запомните няколко ъгли на таблица и съответните им стойности и след това да ги използвате.

Намерете равни ъгли (вертикални, съответстващи) на тригонометрична окръжност. Можете да стигнете до всяка точка, като използвате сумата или разликата на две стойности на таблицата.

Нека се опитаме да го разберем веднага с пример:

Пример №1. cos(x) = ½

1) Запомнете, че оста cos(x) е хоризонтална ос. Отбелязваме стойността ½ върху него и начертаваме перпендикулярна (лилава) линия, докато се пресече с кръга.

2) Имаме две пресечни точки с кръга, стойността на тези ъгли ще бъде решението на уравнението.

Всичко, което остава да направите, е да намерите тези ъгли.

По-добре е да се справите с малко разходи и да научите значението на синус и косинус за ъгли от 30° до 60°.

Или запомнете този трик:

Номерирайте пръстите си от 0 до 4 от малкия пръст до палеца. Ъгълът се задава между малкия пръст и всеки друг пръст (от 0 до 90).

Например, трябва да намерите sin(π/2): π/2 е палецът, n = 4 заместваме във формулата за синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) - ? π/4 съответства на средния пръст (n = 2) => cos(π/4) = √2/2.

Със стойността cos(x) = ½ от таблицата или използвайки мнемонично правило, намираме x = 60° (първата точка x = +π/3 поради факта, че въртенето е настъпило обратно на часовниковата стрелка (+), ъгълът е показано като черна дъга).

Втората точка съответства на абсолютно същия ъгъл, само че въртенето ще бъде по посока на часовниковата стрелка (−). x = −π/3 (ъгълът е показан от долната черна дъга).

И едно последно нещо, преди най-накрая да ви отворят тайно знаниетригонометрия:

Когато трябва да достигнем „100-те точки“, можем да стигнем до там, като завием с...=-225°=135°=495°=...

Тук е същото! Различните ъгли могат да отразяват една и съща посока.

Можем абсолютно да кажем, че трябва да се завъртите до желания ъгъл и след това можете да завъртите 360° = 2π (в синьо) колкото пъти искате и във всяка посока.

Така, за да стигнете до първата посока 60° можете: ...,60°-360°, 60°, 60°+360°,...

И как да запишете останалите ъгли, не ги записвайте безкраен бройточки? (Иска ми се да можех да видя това☻)

Следователно е правилно да напишете отговора: x = 60 + 360n, където n е цяло число (n∈Ζ) (завъртаме се на 60 градуса и след това се въртим колкото пъти искаме, основното е, че посоката остава същото). По същия начин x = −60 + 360n.

Но се съгласихме, че всичко в окръжност е написано чрез π, така че cos(x) = ½ at x =π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Отговор: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.

Пример №2. 2sinx = √2

Първото нещо, което трябва да направите, е да преместите 2 надясно => sinx=√2/2

1) sin(x) съвпада с оста Y. На оста sin(x) отбелязваме √2/2 и чертаем ⊥ лилава права линия, докато се пресече с кръга.

2) От таблицата sinx = √2/2 при x = π/4 и ще търсим втората точка, като завъртим до π, след което трябва да се върнем обратно към π/4.

Следователно втората точка ще бъде x = π − π/4 = 3π/4, можете също да стигнете до нея с помощта на червените стрелки или по някакъв друг начин.

И нека не забравяме да добавим +2πn, n∈Ζ.

Отговор: 3π/4 + 2πn и π/4 + 2πk, k и n са произволни цели числа.

Пример №3. tan(x + π/4) = √3

Всичко изглежда правилно, тангенсът е равен на числото, но π/4 в тангенса е объркващо. След това правим замяната: y = x + π/4.

tg(y) = √3 вече не изглежда толкова страшно. Нека си спомним къде е допирателната ос.

1) Сега на допирателната ос отбелязваме стойността √3, това е по-високо от 1.

2) Начертайте лилава линия през стойността √3 и началото. Отново при пресичане с кръга се получават 2 точки.

Съгласно мнемоничното правило, за тангенс √3, първата стойност е π/3.

3) За да стигнете до втората точка, можете да добавите π => y = π/3 + π = 4π/3 към първата точка (π/3).

4) Но намерихме само y, нека се върнем на x. y = π/3 + 2πn и y = x + π/4, тогава x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Z.

Втори корен: y = 4π/3 + 2πk и y = x + π/4, тогава x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Сега корените на кръга ще бъдат тук:

Отговор: π/12 + 2πn и 13π/12 + 2πk, k и n- всякакви цели числа.

Разбира се, тези два отговора могат да бъдат комбинирани в един. От 0 завъртете с π/12 и след това всеки корен ще се повтаря на всеки π (180°).

Отговорът може да се запише и по следния начин: π/12 + πn, n∈Ζ.

Пример № 4: −10ctg(x) = 10

Нека преместим (−10) в друга част: cot(x) = −1. Обърнете внимание на стойността -1 на котангенсната ос.

1) Нека начертаем права линия през тази точка и началото.

2) Ще трябва да си спомним отново, когато разделянето на косинуса на синуса ще даде едно (това се случва при π/4). Но това е −1, така че една точка ще бъде −π/4. И ще намерим второто, като завъртим до π и след това обратно до π/4 (π − π/4).

Можете да направите това по различен начин (в червено), но моят съвет към вас: винаги се брои от цели пи стойности(π, 2π, 3π...) по този начин има много по-малък шанс да се объркате.

Не забравяйте да добавите 2πk към всяка точка.

Отговор: 3π/4 + 2πn и −π/4 + 2πk, k и n са произволни цели числа.

Алгоритъм за решаване на тригонометрични уравнения (използвайки примера на cos(x) = − √ 3/2) :

1. Отбелязваме стойността (−√3/2) върху оста на тригонометричната функция (косинуси, това е оста X).
2. Начертаваме права линия, перпендикулярна на оста (косинусите), докато се пресече с окръжността.
3. Точките на пресичане с окръжността ще бъдат корените на уравнението.
4. Стойността на една точка (без значение как ще стигнете до нея)+2πk.

Основите са достатъчни, преди да продължите, затвърдете получените знания.

Глава 15. Тригонометрични уравнения

15.6. Решаване на по-сложни тригонометрични уравнения

В предишните параграфи 3-5 са дадени решения на най-простите тригонометрични уравнения: , и . Към тях чрез идентични трансформации или решаване на помощна задача алгебрично уравнениепо-сложни тригонометрични уравнения, съдържащи няколко тригонометрични функции с еднакви или различни аргументи, се редуцират.

Общата техника за решаване на такива уравнения е да се заменят всички тригонометрични функции, включени в уравнението, с една функция въз основа на формули, свързващи тези функции. Когато решаваме уравнение, ние се стремим да правим трансформации, които водят до уравнения, еквивалентни на даденото. В противен случай трябва да проверите получените корени.

Загубата на корени е често срещана грешка. Други такива грешки са неточното познаване на формулите за решения на най-простите уравнения, както и невъзможността да се намери правилно търсената стойност на дъговата функция.

Нека да разгледаме примерите.

Решете уравнението.

Пример 2. (пример за редукция до един аргумент).

Решете уравнението.

Решение:
Препоръчително е да преминем към аргумента. Работата ни напомня за формулата за синус на двоен аргумент: .
Замествайки в уравнението, получаваме: .
От лявата страна отново ще приложим формулата за двоен аргумент синус, но първо ще умножим двете страни на уравнението по .
; ; .
Получихме най-простото уравнение от типа и приравняваме целия аргумент към решението на най-простото уравнение:
, където .

Решете уравнението.

Решение:
Използвайки една от формулите за намаляване на степента, получаваме .

След заместване в уравнението имаме

Решете уравнението.

Решение:
Прехвърляйки към дясната страна, получаваме, че е равно на:
; ; .
Тук трябваше да отидем чрез увеличаване на степента на уравнението, но получихме възможността да използваме добра техника за решаване - преместете всички членове в една част и разложете получения израз на множители:
.
Приравнявайки всеки фактор поотделно на нула, получаваме набор от уравнения,

което по правило е еквивалентно на това уравнение (изключение от това правило е разгледано в следващия пример).
Решаваме уравнението, имаме
, И .
Решаваме уравнението или , имаме и .

Решете уравнението.

Включване в отговор чужд коренсе счита за сериозна грешка. За да го избегнете, трябва да се уверите, че получените корени не превръщат в нула нито една от функциите в знаменателя на дробта на даденото уравнение (ако има дроби там) и че с тези корени никоя от функциите в оригиналното уравнение губи смисъл (ако е включено там). Трябва да запомните при какви стойности на аргумента функцията изчезва и областта на дефиниция на всяка тригонометрична функция.По аналогия те говорят за област на дефиниция на уравнение (домейнът на допустимите стойности или VA на неизвестното ). Областта на дефиниране на тригонометрично уравнение е обща част(пресечна точка) на областите на дефиниране на лявата и дясната страна на това уравнение. Ако полученият корен не принадлежи към областта на дефиниране на уравнението, тогава той е страничен и трябва да бъде изхвърлен.

Решете уравнението
.

Решение:
Да преминем към една функция. Ако го изразим чрез , получаваме ирационално уравнение, което е нежелателно. Замяна чрез:
; .
Нека решим полученото уравнение като квадратно уравнение по отношение на .
или .
Уравнението няма корени.
За уравнението имаме:
. Но те означават едно и също нечетни числа, така че нека напишем решението по-просто: .

Решете уравнението
.

За получаване хомогенно уравнение(всички членове от една и съща степен - втората) умножете дясната страна по израза, който е равен на .
;
.
Тъй като корените на уравнението не са корените на оригиналното уравнение (това може лесно да се провери чрез заместване), за да преминем към една функция, разделяме двете страни на уравнението на .

Решаваме квадратното уравнение за .
или .
За уравнението имаме: .
За уравнението получаваме .

Решете уравнението.

Нека го изразим чрез и , получаваме
. Тук трябва да е различно от нула (в противен случай уравнението няма смисъл), така че областта на дефиниция на уравнението е всичко. Тъй като , ние умножаваме двете страни на уравнението по, за да се отървем от дробите.
;
;
.
За уравнението, което имаме