Цели на урока:
Студентите трябва да знаят:
- какво се нарича наклон на линия;
- ъгълът между правата и оста Ox;
- какъв е геометричният смисъл на производната;
- уравнение на допирателната към графиката на функция;
- метод за построяване на допирателна към парабола;
- да могат да прилагат теоретичните знания на практика.
Цели на урока:
Образователни: създаване на условия учениците да овладеят система от знания, умения и способности с понятията за механичен и геометричен смисъл на производната.
Образователни: формиране на научен мироглед у учениците.
Развитие: развиване на познавателния интерес, творчеството, волята, паметта, речта, вниманието, въображението, възприятието на учениците.
Методи за организиране на образователни и познавателни дейности:
- визуален;
- практичен;
- по умствена дейност: индуктивна;
- според усвояването на материала: частично търсене, репродуктивно;
- по степен на самостоятелност: лабораторни упражнения;
- стимулиращ: насърчаване;
- контрол: устно фронтално изследване.
План на урока
- Устни упражнения (намерете производната)
- Съобщение на ученик на тема „Причини за математически анализ”.
- Учене на нов материал
- Phys. Само минутка.
- Решаване на задачи.
- Лабораторна работа.
- Обобщаване на урока.
- Коментиране на домашни.
Оборудване: мултимедиен проектор (презентация), карти ( лабораторна работа).
По време на часовете
„Човек постига нещо само там, където вярва в собствените си сили“
Л. Фойербах
I. Организационен момент.
Организация на класа през целия урок, готовност на учениците за урока, ред и дисциплина.
Поставяне на учебни цели на учениците, както за целия урок, така и за отделните му етапи.
Определете значението на изучавания материал както в тази тема, така и в целия курс.
Устно броене
1. Намерете производни:
", ()", (4sin x)", (cos2x)", (tg x)", "
2. Логически тест.
а) Въведете пропуснатия израз.
| 5x 3 -6x | 15x 2 -6 | 30x |
| 2sinx | 2cosx… | |
| cos2x | … … |
II. Съобщение на студента по темата „Причини за появата на математическия анализ“.
Общата посока на развитие на науката в крайна сметка се определя от изискванията на практиката на човешката дейност. Съществуването на древни държави със сложна йерархична система на управление би било невъзможно без достатъчното развитие на аритметиката и алгебрата, тъй като събирането на данъци, организирането на армейските доставки, изграждането на дворци и пирамиди и създаването на напоителни системи изискват сложни изчисления. През Ренесанса се разширяват връзките между различните части на средновековния свят, развиват се търговията и занаятите. Започва бързо нарастване на техническото ниво на производство и промишлено се използват нови източници на енергия, които не са свързани с мускулните усилия на хора или животни. През XI-XII век се появяват пълнежни и тъкачни машини, а в средата на XV - печатарска преса. Поради необходимостта от бързо развитиеобщественото производство през този период се променя същността на естествените науки, които от древността са имали описателен характер. Целта на естествознанието е задълбочено проучванеприродни процеси, а не предмети. Математиката, която оперира с постоянни величини, съответства на описателната естествена наука на древността. Беше необходимо да се създаде математически апарат, който да описва не резултата от процеса, а естеството на неговия поток и присъщите му модели. В резултат на това до края на 12 век Нютон в Англия и Лайбниц в Германия завършват първия етап от създаването на математическия анализ. Какво е "математически анализ"? Как могат да се характеризират и предвидят характеристиките на всеки процес? Използване на тези функции? За да проникнете по-дълбоко в същността на определено явление?
III. Учене на нов материал.
Нека да следваме пътя на Нютон и Лайбниц и да видим как можем да анализираме процеса, като го разглеждаме като функция на времето.
Нека представим няколко концепции, които ще ни помогнат допълнително.
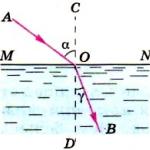
Графиката на линейната функция y=kx+ b е права линия, числото k се нарича наклона на правата линия. k=tg, където е ъгълът на правата линия, тоест ъгълът между тази права линия и положителната посока на оста Ox.

Снимка 1

Разгледайте графиката на функцията y=f(x). Нека начертаем секанс през произволни две точки, например секанс AM. (фиг.2)
Ъглов коефициент на секущата k=tg. В правоъгълен триъгълник AMC<МАС = (объясните почему?). Тогда tg = = , что с точки зрения физики есть величина средней скорости протекания любого процесса на данном промежутке времени, например, скорости изменения расстояния в механике.

Фигура 2

Фигура 3
Самият термин "скорост" характеризира зависимостта на промяната на една величина от промяната на друга, като последната не е задължително да е време.
И така, тангенсът на ъгъла на наклона на секанса tg = .
Ние се интересуваме от зависимостта на промените в количествата за по-кратък период от време. Нека насочим нарастването на аргумента към нула. Тогава дясната страна на формулата е производната на функцията в точка А (обяснете защо). Ако x -> 0, тогава точка M се движи по графиката до точка A, което означава, че правата AM се доближава до някаква права линия AB, което е допирателна към графиката на функцията y = f(x) в точка A. (фиг.3)
Ъгълът на наклона на секанса клони към ъгъла на наклона на допирателната.
Геометрично значениепроизводна е, че стойността на производната в точка е равна на наклона на допирателната към графиката на функцията в точката.
Механично значение на производната.
Тангенсът на допирателния ъгъл е стойност, показваща моментната скорост на промяна на функцията в дадена точка, т.е. нова характеристика на процеса, който се изучава. Лайбниц нарече това количество производна, а Нютон каза, че самата производна се нарича моментна скорост.
IV. Физкултурна минута.
V. Решаване на проблеми.
№ 91 (1) страница 91 – покажете на дъската.
Ъгловият коефициент на допирателната към кривата f(x) = x 3 в точка x 0 – 1 е стойността на производната на тази функция при x = 1. f’(1) = 3x 2 ; f’(1) = 3.
No 91 (3.5) – диктовка.
No 92(1) – на дъската по желание.
№ 92 (3) – самостоятелно с устно изпитване.
№ 92 (5) – на дъската.
Отговори: 45 0, 135 0, 1,5 e 2.
VI. Лабораторна работа.
Цел: да се развие концепцията за „механично значение на производна“.
Приложения на производните в механиката.
Законът е определен праволинейно движениеточки x = x(t), t.
- Средна скорост на движение за определен период от време;
- Скорост и ускорение в момент t 04
- Моменти на спиране; дали точката след момента на спиране продължава да се движи в същата посока или започва да се движи в обратна посока;
- Най-високата скорост на движение за определен период от време.
Работата се изпълнява по 12 варианта, като задачите са диференцирани по ниво на трудност (първият вариант е най-ниското ниво на трудност).
Преди започване на работа разговор по следните въпроси:
- Какъв е физическият смисъл на производната на изместването? (Скорост).
- Възможно ли е да се намери производната на скоростта? Тази величина използва ли се във физиката? Как се нарича? (Ускорение).
- Мигновена скоростравно на нула. Какво може да се каже за движението на тялото в този момент? (Това е моментът на спиране).
- Какъв е физическият смисъл на следните твърдения: производната на движението е равна на нула в точка t 0; променя ли производната знак при преминаване през точка t 0? (Тялото спира; посоката на движение се променя на противоположната).
Образец на студентска работа.
x(t)= t 3 -2 t 2 +1, t 0 = 2.

Фигура 4
В обратна посока.
Нека начертаем схематична диаграма на скоростта. В точката се постига най-висока скорост
t=10, v (10) =3· 10 2 -4· 10 =300-40=260

Фигура 5
VII. Обобщаване на урока
1) Какво е геометричното значение на производната?
2) Какво е механичното значение на производното?
3) Направете заключение за работата си.
VIII. Коментиране на домашни.
Страница 90. №91(2,4,6), №92(2,4,6,), стр.92 №112.
Използвани книги
- Учебник Алгебра и началото на анализа.
Автори: Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунина.
Под редакцията на А. Б. Жижченко. - Алгебра 11 клас. Урочни плановепо учебника на Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров. Част 1.
- Интернет ресурси: http://orags.narod.ru/manuals/html/gre/12.jpg
Преди да прочетете информацията на текущата страница, препоръчваме да гледате видеоклип за производната и нейното геометрично значение
Вижте също пример за изчисляване на производната в точка
Допирателната към правата l в точка M0 е правата линия M0T - граничната позиция на секущата M0M, когато точката M клони към M0 по тази права (т.е. ъгълът клони към нула) по произволен начин.
Производна на функцията y = f(x)в точка х0 Нареченграницата на отношението на нарастването на тази функция към увеличението на аргумента, когато последният клони към нула. Производната на функцията y = f(x) в точката x0 и в учебниците се означава със символа f"(x0). Следователно по дефиниция
Терминът "дериват"(също "втора производна") въведен от Ж. Лагранж(1797), освен това той дава обозначенията y’, f’(x), f”(x) (1770,1779). Обозначението dy/dx се появява за първи път в Лайбниц (1675).
Производната на функцията y = f(x) при x = xo е равна на наклона на допирателната към графиката на тази функция в точката Mo(xo, f(xo)), т.е.
![]() къде - допирателен ъгъл
към оста Ox на правоъгълната декартова координатна система.
къде - допирателен ъгъл
към оста Ox на правоъгълната декартова координатна система.
 Уравнение на тангенс
към правата y = f(x) в точката Mo(xo, yo) приема формата
Уравнение на тангенс
към правата y = f(x) в точката Mo(xo, yo) приема формата
Нормалната към крива в дадена точка е перпендикулярът на допирателната в същата точка. Ако f(x0) не е равно на 0, тогава нормално уравнение на линията y = f(x) в точката Mo(ho, yo) ще бъде записано както следва:

Физическо значение на производната
Ако x = f(t) е законът за праволинейно движение на точка, тогава x’ = f’(t) е скоростта на това движение в момент t. Дебитфизични, химични и други процесите се изразяват с помощта на производната.
Ако съотношението dy/dx за x->x0 има граница отдясно (или отляво), тогава то се нарича производна отдясно (съответно производна отляво). Такива граници се наричат едностранни производни.

 Очевидно функция f(x), дефинирана в определена околност на точката x0, има производна f’(x) тогава и само ако едностранните производни съществуват и са равни една на друга.
Очевидно функция f(x), дефинирана в определена околност на точката x0, има производна f’(x) тогава и само ако едностранните производни съществуват и са равни една на друга.
Геометрична интерпретация на производнататъй като наклонът на допирателната към графиката се отнася и за този случай: допирателната в в такъв случайуспоредна на оста Oy.
 За функция, която има производна в дадена точка, се казва, че е диференцируема в тази точка. Функция, която има производна във всяка точка от даден интервал, се нарича диференцируема в този интервал. Ако интервалът е затворен, то в краищата му има едностранни производни.
За функция, която има производна в дадена точка, се казва, че е диференцируема в тази точка. Функция, която има производна във всяка точка от даден интервал, се нарича диференцируема в този интервал. Ако интервалът е затворен, то в краищата му има едностранни производни.
Операцията за намиране на производната се нарича.
Статията предоставя подробно обяснение на дефинициите, геометричното значение на производната с графични означения. Уравнението на допирателна ще бъде разгледано с примери, ще бъдат намерени уравненията на допирателна към криви от 2-ри ред.
Определение 1Ъгълът на наклона на правата линия y = k x + b се нарича ъгъл α, който се измерва от положителната посока на оста x към правата линия y = k x + b в положителната посока.
На фигурата посоката x е обозначена със зелена стрелка и зелена дъга, а ъгълът на наклона с червена дъга. Синята линия се отнася за правата линия.
Определение 2
Наклонът на правата линия y = k x + b се нарича числов коефициент k.
Ъгловият коефициент е равен на тангенса на правата линия, с други думи k = t g α.
- Ъгълът на наклона на права линия е равен на 0 само ако е успоредна на x и наклонът е равен на нула, тъй като тангенсът на нулата е равен на 0. Това означава, че формата на уравнението ще бъде y = b.
- Ако ъгълът на наклона на правата линия y = k x + b е остър, тогава условията 0 са изпълнени< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положително число, тъй като стойността на тангенса удовлетворява условието t g α > 0 и има увеличение на графиката.
- Ако α = π 2, тогава местоположението на правата е перпендикулярно на x. Равенството се определя от x = c, като стойността c е реално число.
- Ако ъгълът на наклона на правата линия y = k x + b е тъп, тогава той съответства на условията π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицателно значение, а графиката намалява.
Секансът е права, която минава през 2 точки на функцията f (x). С други думи, секансът е права линия, която се прекарва през произволни две точки на графиката дадена функция.

Фигурата показва, че A B е секанс, а f (x) е черна крива, α е червена дъга, показваща ъгъла на наклон на секанса.
Когато ъгловият коефициент на права линия е равен на тангенса на ъгъла на наклона, ясно е, че тангенса на правоъгълен триъгълник A B C може да се намери чрез съотношението на срещуположната страна към съседната.
Определение 4
Получаваме формула за намиране на секанс от формата:
k = t g α = B C A C = f (x B) - f x A x B - x A, където абсцисите на точки A и B са стойностите x A, x B и f (x A), f (x B) са функциите на стойностите в тези точки.
Очевидно ъгловият коефициент на секанса се определя с помощта на равенството k = f (x B) - f (x A) x B - x A или k = f (x A) - f (x B) x A - x B и уравнението трябва да бъде написано като y = f (x B) - f (x A) x B - x A x - x A + f (x A) или
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .
Секансът разделя графиката визуално на 3 части: вляво от точка A, от A до B, вдясно от B. Фигурата по-долу показва, че има три секанса, които се считат за съвпадащи, т.е. те са зададени с помощта на подобно уравнение.

По дефиниция е ясно, че правата линия и нейният секанс в този случай съвпадат.
Секансът може да пресича графиката на дадена функция многократно. Ако има уравнение от вида y = 0 за секанс, тогава броят на точките на пресичане със синусоидата е безкраен.
Определение 5
Допирателна към графиката на функцията f (x) в точка x 0 ; f (x 0) е права линия, минаваща през дадена точка x 0; f (x 0), с наличието на сегмент, който има много x стойности, близки до x 0.
Пример 1
Нека разгледаме по-отблизо примера по-долу. Тогава е ясно, че правата, определена от функцията y = x + 1, се счита за допирателна към y = 2 x в точката с координати (1; 2). За по-голяма яснота е необходимо да се разгледат графики със стойности, близки до (1; 2). Функцията y = 2 x е показана в черно, синята линия е допирателната, а червената точка е пресечната точка.

Очевидно y = 2 x се слива с правата y = x + 1.
За да определим допирателната, трябва да разгледаме поведението на допирателната A B, когато точка B се приближава безкрайно до точка A. За яснота представяме чертеж.

Секущата A B, обозначена със синята линия, клони към позицията на самата допирателна, а ъгълът на наклон на секущата α ще започне да клони към ъгъла на наклон на самата допирателна α x.
Определение 6
Допирателната към графиката на функцията y = f (x) в точка A се счита за гранична позиция на секанса A B, когато B клони към A, т.е. B → A.
Сега нека преминем към разглеждане на геометричния смисъл на производната на функция в точка.
Нека преминем към разглеждане на секанса A B за функцията f (x), където A и B с координати x 0, f (x 0) и x 0 + ∆ x, f (x 0 + ∆ x), а ∆ x е се обозначава като нарастване на аргумента. Сега функцията ще приеме формата ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . За по-голяма яснота нека дадем пример за чертеж.

Разгледайте получения правоъгълен триъгълник A B C. Използваме дефиницията на допирателната за решаване, т.е. получаваме връзката ∆ y ∆ x = t g α . От определението за допирателна следва, че lim ∆ x → 0 ∆ y ∆ x = t g α x . Съгласно правилото за производната в точка имаме, че производната f (x) в точката x 0 се нарича граница на съотношението на увеличението на функцията към увеличението на аргумента, където ∆ x → 0 , тогава го означаваме като f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
От това следва, че f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, където k x е означено като наклон на допирателната.
Тоест, откриваме, че f '(x) може да съществува в точка x 0 и подобно на допирателната към дадена графика на функцията в точката на допиране, равна на x 0, f 0 (x 0), където стойността на наклонът на тангентата в точката е равен на производната в точка x 0 . Тогава получаваме, че k x = f " (x 0) .
Геометричният смисъл на производната на функция в точка е, че дава концепцията за съществуването на допирателна към графиката в същата точка.
За да напишете уравнението на която и да е права линия в равнина, е необходимо да имате ъглов коефициент с точката, през която тя минава. Неговото обозначение се приема като x 0 при пресичане.
Уравнението на допирателната към графиката на функцията y = f (x) в точката x 0, f 0 (x 0) приема формата y = f "(x 0) x - x 0 + f (x 0).
Това означава, че крайната стойност на производната f "(x 0) може да определи позицията на допирателната, тоест вертикално, при условие че lim x → x 0 + 0 f "(x) = ∞ и lim x → x 0 - 0 f "(x ) = ∞ или изобщо отсъствие при условието lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .
Местоположението на допирателната зависи от стойността на нейния ъглов коефициент k x = f "(x 0). Когато е успоредна на оста o x, получаваме, че k k = 0, когато е успоредна на o y - k x = ∞, и формата на допирателното уравнение x = x 0 нараства с k x > 0, намалява с k x< 0 .
Пример 2
Съставете уравнение за допирателната към графиката на функцията y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 в точката с координати (1; 3) и определете ъгъла на наклона.
Решение
По условие имаме, че функцията е дефинирана за всички реални числа. Откриваме, че точката с координати, зададени от условието, (1; 3) е точка на допиране, тогава x 0 = - 1, f (x 0) = - 3.
Необходимо е да се намери производната в точката със стойност - 1. Разбираме това
y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Стойността на f' (x) в точката на допирателна е наклонът на тангентата, който е равен на тангенса на наклона.
Тогава k x = t g α x = y " (x 0) = 3 3
От това следва, че α x = a r c t g 3 3 = π 6
Отговор:уравнението на допирателната приема формата
y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3
За по-голяма яснота даваме пример в графична илюстрация.
Черният цвят се използва за графиката на оригиналната функция, Син цвят– изображение на допирателна, червена точка – точка на допиране. Фигурата вдясно показва увеличен изглед.

Пример 3
Установете съществуването на допирателна към графиката на дадена функция
y = 3 · x - 1 5 + 1 в точката с координати (1 ; 1) . Напишете уравнение и определете ъгъла на наклона.
Решение
По условие имаме, че домейнът на дефиниция на дадена функция се счита за набор от всички реални числа.
Нека да преминем към намирането на производната
y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Ако x 0 = 1, тогава f' (x) е недефинирано, но границите са записани като lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , което означава, че съществуваща вертикална допирателна в точка (1; 1).
Отговор:уравнението ще приеме формата x = 1, където ъгълът на наклон ще бъде равен на π 2.
За по-голяма яснота нека го изобразим графично.

Пример 4
Намерете точките върху графиката на функцията y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, където
- Няма допирателна;
- Допирателната е успоредна на x;
- Допирателната е успоредна на правата y = 8 5 x + 4.
Решение
Необходимо е да се обърне внимание на обхвата на дефиницията. По условие имаме, че функцията е дефинирана върху множеството от всички реални числа. Разширяваме модула и решаваме системата с интервали x ∈ - ∞ ; 2 и [-2; + ∞). Разбираме това
y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)
Необходимо е да се разграничи функцията. Ние имаме това
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 ", x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)
Когато x = − 2, тогава производната не съществува, тъй като едностранните граници не са равни в тази точка:
lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Изчисляваме стойността на функцията в точката x = - 2, където получаваме това
- y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, тоест допирателната в точката ( - 2; - 2) няма да съществува.
- Допирателната е успоредна на x, когато наклонът е нула. Тогава k x = t g α x = f "(x 0). Това означава, че е необходимо да се намерят стойностите на такъв x, когато производната на функцията го превръща в нула. Тоест стойностите на f ' (x) ще бъдат точките на допиране, където допирателната е успоредна на x.
Когато x ∈ - ∞ ; - 2, тогава - 1 5 (x 2 + 12 x + 35) = 0 и за x ∈ (- 2; + ∞) получаваме 1 5 (x 2 - 4 x + 3) = 0.
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
Изчислете стойностите на съответните функции
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Следователно - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 се считат за търсените точки от графиката на функцията.
Нека да разгледаме графично представяне на решението.

Черната линия е графиката на функцията, червените точки са точките на допир.
- Когато линиите са успоредни, ъгловите коефициенти са равни. След това е необходимо да се търсят точки на графиката на функцията, където наклонът ще бъде равен на стойността 8 5. За да направите това, трябва да решите уравнение под формата y "(x) = 8 5. Тогава, ако x ∈ - ∞; - 2, получаваме, че - 1 5 (x 2 + 12 x + 35) = 8 5 и ако x ∈ ( - 2 ; + ∞), тогава 1 5 (x 2 - 4 x + 3) = 8 5.
Първото уравнение няма корени, тъй като дискриминантът е по-малък от нула. Нека запишем това
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
Друго уравнение има две истински корени, Тогава
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
Нека да преминем към намирането на стойностите на функцията. Разбираме това
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Точки със стойности - 1; 4 15, 5; 8 3 са точките, в които допирателните са успоредни на правата y = 8 5 x + 4.
Отговор:черна линия – графика на функцията, червена линия – графика на y = 8 5 x + 4, синя линия – допирателни в точки - 1; 4 15, 5; 8 3.

Възможно съществуване безкраен бройдопирателни за дадени функции.
Пример 5
Напишете уравненията на всички налични тангенси на функцията y = 3 cos 3 2 x - π 4 - 1 3, които са разположени перпендикулярно на правата линия y = - 2 x + 1 2.
Решение
За да се състави уравнението на допирателната, е необходимо да се намерят коефициентът и координатите на допирателната точка въз основа на условието за перпендикулярност на линиите. Дефиницията е следната: произведението на ъгловите коефициенти, които са перпендикулярни на прави линии, е равно на - 1, тоест записано като k x · k ⊥ = - 1. От условието имаме, че ъгловият коефициент е разположен перпендикулярно на правата и е равен на k ⊥ = - 2, тогава k x = - 1 k ⊥ = - 1 - 2 = 1 2.
Сега трябва да намерите координатите на допирните точки. Трябва да намерите x и след това неговата стойност за дадена функция. Обърнете внимание, че от геометричния смисъл на производната в точката
x 0 получаваме, че k x = y "(x 0). От това равенство намираме стойностите на x за точките на контакт.
Разбираме това
y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9
Това тригонометрично уравнениеще се използва за изчисляване на ординатите на допирателните точки.
3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk или 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk или 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z е набор от цели числа.
Намерени са x допирни точки. Сега трябва да преминете към търсене на стойностите на y:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 или y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 или y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 или y 0 = - 4 5 + 1 3
От това получаваме, че 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 са точките на допир.
Отговор:необходимите уравнения ще бъдат записани като
y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
За визуално представяне разгледайте функция и допирателна върху координатна права.
Фигурата показва, че функцията се намира на интервала [ - 10 ; 10 ], където черната линия е графиката на функцията, сините линии са допирателни, които са разположени перпендикулярно на дадената права от вида y = - 2 x + 1 2. Червените точки са допирни точки.

Каноничните уравнения на криви от 2-ри ред не са еднозначни функции. Тангентните уравнения за тях се съставят по известни схеми.
Допирателна към окръжност
За определяне на окръжност с център в точка x c e n t e r ; y c e n t e r и радиус R, приложете формулата x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .
Това равенство може да се запише като обединение на две функции:
y = R 2 - x - x център 2 + y център y = - R 2 - x - x център 2 + y център
Първата функция се намира отгоре, а втората отдолу, както е показано на фигурата.

Да се състави уравнение на окръжност в точка x 0; y 0 , който се намира в горния или долния полукръг, трябва да намерите уравнението на графиката на функция от вида y = R 2 - x - x c e n t e r 2 + y c e n t e r или y = - R 2 - x - x c e n t e r 2 + y c e n t e r в посочената точка.
Когато в точки x c e n t e r ; y център + R и x център; y c e n t e r - R допирателните могат да бъдат дадени чрез уравненията y = y c e n t e r + R и y = y c e n t e r - R , и в точки x c e n t e r + R ; y c e n t e r и
x c e n t e r - R; y c e n t e r ще бъде успореден на o y, тогава получаваме уравнения от вида x = x c e n t e r + R и x = x c e n t e r - R .

Допирателна към елипса
Когато елипсата има център в x c e n t e r ; y c e n t e r с полуоси a и b, то може да се уточни с помощта на уравнението x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.
Елипса и кръг могат да бъдат обозначени чрез комбиниране на две функции, а именно горната и долната полуелипса. Тогава разбираме това
y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Ако допирателните са разположени във върховете на елипсата, тогава те са успоредни около x или около y. По-долу, за по-голяма яснота, разгледайте фигурата.

Пример 6
Напишете уравнението на допирателната към елипсата x - 3 2 4 + y - 5 2 25 = 1 в точки със стойности на x, равни на x = 2.
Решение
Необходимо е да се намерят допирателните точки, които съответстват на стойността x = 2. Заместваме в съществуващото уравнение на елипсата и намираме това
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
След това 2; 5 3 2 + 5 и 2; - 5 3 2 + 5 са допирателните точки, които принадлежат на горната и долната полуелипсата.
Нека да преминем към намирането и решаването на уравнението на елипсата по отношение на y. Разбираме това
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Очевидно горната полуелипса е определена с помощта на функция от формата y = 5 + 5 2 4 - x - 3 2, а долната полуелипса y = 5 - 5 2 4 - x - 3 2.
Нека приложим стандартен алгоритъм, за да създадем уравнение за допирателна към графиката на функция в точка. Нека запишем, че уравнението за първата допирателна в точка 2; 5 3 2 + 5 ще изглежда така
y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Откриваме, че уравнението на втората допирателна със стойност в точката
2 ; - 5 3 2 + 5 приема формата
y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Графично тангентите се означават, както следва:

Допирателна към хипербола
Когато хипербола има център в x c e n t e r ; y c e n t e r и върхове x c e n t e r + α ; y c e n t e r и x c e n t e r - α; y c e n t e r се изпълнява неравенството x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, ако с върхове x c e n t e r ; y център + b и x център; y c e n t e r - b , тогава се определя с помощта на неравенството x-x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Една хипербола може да бъде представена като две комбинирани функции на формата
y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r или y = b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r y = - b a · (x - x център) 2 + a 2 + y център

В първия случай имаме, че допирателните са успоредни на y, а във втория са успоредни на x.
От това следва, че за да се намери уравнението на допирателната към хипербола, е необходимо да се установи на коя функция принадлежи точката на допирателна. За да се определи това, е необходимо да се замени в уравненията и да се провери за идентичност.
Пример 7
Напишете уравнение за допирателната към хиперболата x - 3 2 4 - y + 3 2 9 = 1 в точка 7; - 3 3 - 3 .
Решение
Необходимо е да се трансформира записът на решението за намиране на хипербола с помощта на 2 функции. Разбираме това
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 и y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Необходимо е да се установи към коя функция принадлежи дадена точка с координати 7; - 3 3 - 3 .
Очевидно за проверка на първата функция е необходимо y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, тогава точката не принадлежи на графиката, тъй като равенството не важи.
За втората функция имаме, че y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, което означава, че точката принадлежи на дадената графика. От тук трябва да намерите склона.
Разбираме това
y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
Отговор:уравнението на допирателната може да бъде представено като
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Ясно е изобразено така:

Тангента на парабола
За да създадете уравнение за допирателната към параболата y = a x 2 + b x + c в точката x 0, y (x 0), трябва да използвате стандартен алгоритъм, след което уравнението ще приеме формата y = y "(x 0) x - x 0 + y ( x 0). Такава допирателна във върха е успоредна на x.
Трябва да дефинирате параболата x = a y 2 + b y + c като обединение на две функции. Следователно трябва да решим уравнението за y. Разбираме това
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Графично изобразен като:

За да разберете дали точка x 0, y (x 0) принадлежи на функция, продължете внимателно според стандартния алгоритъм. Такава допирателна ще бъде успоредна на o y спрямо параболата.
Пример 8
Напишете уравнението на допирателната към графиката x - 2 y 2 - 5 y + 3, когато имаме ъгъл на допирателната от 150 °.
Решение
Започваме решението, като представяме параболата като две функции. Разбираме това
2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 х - 4
Стойността на наклона е равна на стойността на производната в точка x 0 на тази функция и е равна на тангенса на ъгъла на наклон.
Получаваме:
k x = y "(x 0) = t g α x = t g 150 ° = - 1 3
От тук определяме стойността на x за точките на контакт.
Първата функция ще бъде написана като
y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Очевидно няма реални корени, тъй като получихме отрицателна стойност. Заключаваме, че за такава функция няма тангенс с ъгъл 150°.
Втората функция ще бъде написана като
y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Имаме, че допирните точки са 23 4 ; - 5 + 3 4 .
Отговор:уравнението на допирателната приема формата
y = - 1 3 x - 23 4 + - 5 + 3 4
Нека го изобразим графично по следния начин:

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter
Предмет. Производна. Геометричен и механичен смисъл на производната
Ако тази граница съществува, тогава се казва, че функцията е диференцируема в точка. Производната на функция се означава с (формула 2).

- Геометрично значение на производната. Нека да разгледаме графиката на функцията. От фиг. 1 става ясно, че за всеки две точки A и B от графиката на функцията може да се напише формула 3). Той съдържа ъгъла на наклона на секущата AB.
По този начин съотношението на разликата е равно на наклона на секанса. Ако фиксирате точка A и преместите точка B към нея, тогава тя намалява неограничено и се доближава до 0, а секансът AB се доближава до допирателната AC. Следователно границата на съотношението на разликата е равна на наклона на допирателната в точка А. Това води до заключението.
Производната на функция в точка е наклонът на допирателната към графиката на тази функция в тази точка. Това е геометричното значение на производната.
- Уравнение на тангенс . Нека изведем уравнението на допирателната към графиката на функцията в точка. В общия случай уравнението на права линия с ъглов коефициент има вида: . За да намерим b, се възползваме от факта, че допирателната минава през точка A: . Това предполага: . Замествайки този израз вместо b, получаваме уравнението на допирателната (формула 4).

Производната на функция е една от трудните теми в училищна програма. Не всеки завършил ще отговори на въпроса какво е производно.
Тази статия обяснява по прост и ясен начин какво е дериват и защо е необходим.. Сега няма да се стремим към математическа строгост в презентацията. Най-важното е да разберете смисъла.
Нека си припомним определението:
Производната е скоростта на промяна на функция.
Фигурата показва графики на три функции. Според вас кой расте по-бързо?

Отговорът е очевиден - третият. Той има най-високата скорост на промяна, тоест най-голямата производна.
Ето още един пример.
Костя, Гриша и Матвей получиха работа едновременно. Нека видим как са се променили доходите им през годината:

Графиката показва всичко наведнъж, нали? Доходите на Костя се удвоиха за шест месеца. И доходите на Гриша също се увеличиха, но съвсем малко. И доходите на Матвей намаляха до нула. Началните условия са същите, но скоростта на промяна на функцията, т.е производна, - различен. Що се отнася до Матвей, неговата производна на доходите като цяло е отрицателна.
Интуитивно, ние лесно оценяваме скоростта на промяна на функция. Но как да направим това?
Това, което наистина гледаме, е колко стръмно се издига (или надолу) графиката на дадена функция. С други думи, колко бързо се променя y при промяна на x? Очевидно една и съща функция в различни точки може да има различен смисълпроизводна - тоест може да се променя по-бързо или по-бавно.
Производната на функция се обозначава.
Ще ви покажем как да го намерите с помощта на графика.

Начертана е графика на някаква функция. Нека вземем точка с абциса върху нея. Нека начертаем допирателна към графиката на функцията в тази точка. Искаме да преценим колко стръмно се изкачва графиката на дадена функция. Удобна стойност за това е тангенс на допирателния ъгъл.
Производната на функция в точка е равна на тангенса на допирателния ъгъл, начертан към графиката на функцията в тази точка.
Моля, обърнете внимание, че като ъгъл на наклон на допирателната приемаме ъгъла между допирателната и положителната посока на оста.
Понякога учениците питат какво е допирателна към графиката на функция. Това е права линия, която има една обща точка с графиката в този раздел и както е показано на нашата фигура. Изглежда като допирателна към окръжност.
Нека го намерим. Спомняме си, че тангенса на остър ъгъл в правоъгълен триъгълникравно на съотношението на срещуположната страна към съседната страна. От триъгълника:
Намерихме производната с помощта на графика, без дори да знаем формулата на функцията. Такива проблеми често се срещат в Единния държавен изпит по математика под номера.
Има и друга важна връзка. Спомнете си, че правата линия е дадена от уравнението
Величината в това уравнение се нарича наклон на права линия. Тя е равна на тангенса на ъгъла на наклона на правата спрямо оста.
.
Разбираме това
Нека запомним тази формула. Той изразява геометричния смисъл на производната.
Производната на функция в точка е равна на наклона на допирателната, начертана към графиката на функцията в тази точка.
С други думи, производната е равна на тангенса на допирателния ъгъл.
Вече казахме, че една и съща функция може да има различни производни в различни точки. Нека видим как производната е свързана с поведението на функцията.
Нека начертаем графика на някаква функция. Нека тази функция нараства в някои области и намалява в други, и то с различна скорост. И нека тази функция има максимални и минимални точки.

В даден момент функцията се увеличава. Допирателната към графиката, начертана в точка, образува остър ъгъл с положителната посока на оста. Това означава, че производната в точката е положителна.
В момента нашата функция намалява. Допирателната в тази точка образува тъп ъгъл с положителната посока на оста. Тъй като допирателната тъп ъгъле отрицателна, в точката производната е отрицателна.
Ето какво се случва:
Ако една функция нараства, нейната производна е положителна.
Ако намалява, производната му е отрицателна.
Какво ще се случи при максималните и минималните точки? Виждаме, че в точките (максимална точка) и (минимална точка) допирателната е хоризонтална. Следователно тангенсът на допирателната в тези точки е нула и производната също е нула.
Точка - максимална точка. В този момент нарастването на функцията се заменя с намаление. Следователно знакът на производната се променя в точката от „плюс“ на „минус“.
В точката - минималната точка - производната също е нула, но нейният знак се променя от "минус" на "плюс".
Извод: с помощта на производната можем да разберем всичко, което ни интересува за поведението на дадена функция.
Ако производната е положителна, тогава функцията нараства.
Ако производната е отрицателна, тогава функцията намалява.
В максималната точка производната е нула и променя знака от "плюс" на "минус".
В минималната точка производната също е нула и променя знака от „минус“ на „плюс“.
Нека напишем тези изводи под формата на таблица:
| се увеличава | максимална точка | намалява | минимална точка | се увеличава | |
| + | 0 | - | 0 | + |
Нека направим две малки уточнения. Един от тях ще ви трябва, когато решавате Проблеми на единния държавен изпит. Друг – през първата година, с по-сериозно изучаване на функции и производни.
Възможно е производната на функция в дадена точка да е равна на нула, но функцията да няма нито максимум, нито минимум в тази точка. Това е т.нар :

В дадена точка допирателната към графиката е хоризонтална и производната е нула. Въпреки това, преди точката функцията нараства - и след точката тя продължава да нараства. Знакът на производната не се променя - тя остава положителна, както е била.
Също така се случва в точката на максимум или минимум производната да не съществува. На графиката това съответства на рязко прекъсване, когато е невъзможно да се начертае допирателна в дадена точка.

Как да намерим производната, ако функцията е дадена не с графика, а с формула? В този случай се прилага