Класификация на сигналите и техните параметри.
Електрическите сигнали са електрически процеси, използвани за предаване или съхраняване на информация.
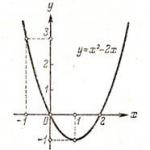
Сигналите могат да бъдат разделени на два големи класа: детерминистични и случайни. Детерминистичните сигнали са тези, чиито моментни стойности по всяко време могат да бъдат предвидени с вероятност, равна на единица, и които са определени под формата на някаква специфична функция на времето. Нека дадем някои типични примери: хармоничен сигнал с известна амплитуда Аи точка T(фиг. 1.1 А); последователност от правоъгълни импулси с известен период на повторение T, продължителност t и амплитуда А(фиг. 1.1 b); последователност от импулси с произволна форма с известна продължителност t и амплитуда Аи точка T(фиг. 1.1 V). Детерминистичните сигнали не съдържат никаква информация.
Случайните сигнали са хаотични функции на времето, чиито стойности са предварително неизвестни и не могат да бъдат предвидени с вероятност равна на единица (единичен импулс с продължителност t и амплитуда А(фиг. 1.1 Ж) реч, музика в израз на електрически величини). Случайните сигнали също включват шум.
Детерминираните сигнали от своя страна се разделят на периодични, за които условието е изпълнено С(T)=С(t+kT), Където T- Период, к- произволно цяло число и под С(T) се отнася до промяна на тока, напрежението или заряда във времето (фиг. 1.1 a B C).
Очевидно всеки детерминиран сигнал, за който е изпълнено условието, е непериодичен: С(T)¹ С(t+kT).
Най-простият периодичен сигнал е хармоничен сигнал от формата  .
.
Всеки сложен периодичен сигнал може да бъде разложен на хармонични компоненти. По-долу ще бъде извършено такова разлагане за няколко специфични типа сигнали.
Високочестотен хармоничен сигнал, в който информацията е вградена чрез модулация, се нарича радиосигнал (фиг. 1.1 д).
Периодични сигнали.
 Всеки сложен периодичен сигнал С(T)=С(t+kT) (фиг. 1.2), зададени в диапазона от стойности Tот –¥ до +¥, могат да бъдат представени като сума от елементарни хармонични сигнали. Това представяне се извършва под формата на ред на Фурие, ако само дадената периодична функция удовлетворява условията на Дирихле:
Всеки сложен периодичен сигнал С(T)=С(t+kT) (фиг. 1.2), зададени в диапазона от стойности Tот –¥ до +¥, могат да бъдат представени като сума от елементарни хармонични сигнали. Това представяне се извършва под формата на ред на Фурие, ако само дадената периодична функция удовлетворява условията на Дирихле:
1. На всеки краен интервал от време функцията С(T) трябва да бъде непрекъснат или да има краен брой прекъсвания от първи вид.
2. В рамките на един период функцията трябва да има краен брой максимуми и минимуми.
Обикновено всички реални радиосигнали отговарят на тези условия. В тригонометрична форма редът на Фурие има формата (1.1)
където постоянният компонент е равен на  (1.2)
(1.2)
и коефициентите а н,И b nза косинусови и синусоидални членове разширенията се определят от изразите  (1.3)
(1.3)
Амплитуда (модул) и фаза (аргумент) n-тохармониците се изразяват чрез коефициенти а н,И b nпо следния начин ![]() (1.4)
(1.4)
Когато се използва сложна форма на запис, изразът за сигнала S(t) приема формата ![]() . Ето коефициентите
. Ето коефициентите ![]() , наречени комплексни амплитуди, са равни
, наречени комплексни амплитуди, са равни  и са свързани с величините a n и b n по формулите: за n>0, а за n<0. С учётом обозначений
и са свързани с величините a n и b n по формулите: за n>0, а за n<0. С учётом обозначений  .
.
Спектърът на периодичната функция се състои от отделни линии, съответстващи на дискретни честоти 0, w, 2w, 3w ..., т.е. има линеен или дискретен характер (фиг. 1.3). Използването на редове на Фурие в комбинация с принципа на суперпозицията е мощно средство за анализиране на влиянието на линейните системи върху преминаването през тях на различни видове периодични сигнали.
Когато разширявате периодична функция в серия на Фурие, трябва да вземете предвид симетрията на самата функция, тъй като това ви позволява да опростите изчисленията. В зависимост от вида на симетрията, функциите, представени от реда на Фурие, могат:
1.  Нямате постоянен компонент, ако площта на фигурата за положителния полупериод е равна на площта на фигурата за отрицателния полупериод.
Нямате постоянен компонент, ако площта на фигурата за положителния полупериод е равна на площта на фигурата за отрицателния полупериод.
2. Не разполагайте с равномерни хармоници и постоянен компонент, ако стойностите на функцията се повтарят след половин период с обратен знак.
Спектрален състав на последователност от правоъгълни импулси в различни периоди от техния работен цикъл.
Периодична последователност от правоъгълни импулси е показана на фиг. 1.4. Постоянният компонент на реда на Фурие се определя от израза  и за този случай е равно на
и за този случай е равно на  .
.
 Амплитуда на компонента cos и нравна на
Амплитуда на компонента cos и нравна на
 и амплитудата на син компонента b nравна на
и амплитудата на син компонента b nравна на ![]() .
.
Амплитуда нти хармоници ![]()

Литература: [Л.1], с. 40
Като пример даваме разширение в ред на Фурие на периодична последователност от правоъгълни импулси с амплитуда, продължителност и период на повторение, симетрични спрямо нулата, т.е.
 , (2.10)
, (2.10)
Тук 
Разширяването на такъв сигнал в ред на Фурие дава
 , (2.11)
, (2.11)
къде е работният цикъл.
За да опростите нотацията, можете да въведете нотацията
 , (2.12)
, (2.12)
Тогава (2.11) ще се запише по следния начин
 , (2.13)
, (2.13)
На фиг. 2.3 показва последователност от правоъгълни импулси. Спектърът на последователността, както и всеки друг периодичен сигнал, е дискретен (линеен) по природа.
Обвивката на спектъра (фиг. 2.3, b) е пропорционална  . Разстоянието по честотната ос между две съседни компоненти на спектъра е , а между две нулеви стойности (ширината на лоба на спектъра) е . Броят на хармоничните компоненти в рамките на един лоб, включително нулевата стойност вдясно на фигурата, е , където знакът означава закръгляване до най-близкото цяло число, по-малко (ако работният цикъл е дробно число), или (ако работният цикъл е цяло число). С увеличаването на периода основната честота
. Разстоянието по честотната ос между две съседни компоненти на спектъра е , а между две нулеви стойности (ширината на лоба на спектъра) е . Броят на хармоничните компоненти в рамките на един лоб, включително нулевата стойност вдясно на фигурата, е , където знакът означава закръгляване до най-близкото цяло число, по-малко (ако работният цикъл е дробно число), или (ако работният цикъл е цяло число). С увеличаването на периода основната честота  намалява, спектралните компоненти в диаграмата се сближават, амплитудите на хармониците също намаляват. В този случай формата на плика се запазва.
намалява, спектралните компоненти в диаграмата се сближават, амплитудите на хармониците също намаляват. В този случай формата на плика се запазва.




При решаване на практически проблеми на спектралния анализ се използват циклични честоти вместо ъглови честоти  , измерено в Херц. Очевидно разстоянието между съседни хармоници на диаграмата ще бъде , а ширината на един лоб на спектъра ще бъде . Тези стойности са представени в скоби в диаграмата.
, измерено в Херц. Очевидно разстоянието между съседни хармоници на диаграмата ще бъде , а ширината на един лоб на спектъра ще бъде . Тези стойности са представени в скоби в диаграмата.
В практическата радиотехника в повечето случаи вместо спектрално представяне (фиг. 2.3, b) се използват спектрални диаграми на амплитудните и фазовите спектри. Амплитудният спектър на последователност от правоъгълни импулси е показан на фиг. 2.3, c.
Очевидно е, че обвивката на амплитудния спектър е пропорционална  .
.
Що се отнася до фазовия спектър (фиг. 2.3, d), се смята, че началните фази на хармоничните компоненти се променят рязко с количеството -π при смяна на знака на плика sinc kπ/q. Началните фази на хармониците на първия лоб се приемат за нула. Тогава ще бъдат началните фази на хармониците на втория лоб φ = -π , трето венчелистче φ = -2πи т.н.
Нека разгледаме друго представяне на сигнала с ред на Фурие. За целта използваме формулата на Ойлер
 .
.
В съответствие с тази формула, k-тият компонент (2.9) на разширението на сигнала в ред на Фурие може да бъде представен, както следва
 ;
;  . (2.15)
. (2.15)
Тук величините и са комплексни и представляват комплексните амплитуди на компонентите на спектъра. След това сериалът
Фурие (2.8), като се вземе предвид (2.14), ще приеме следната форма
 , (2.16)
, (2.16)
 , (2.17)
, (2.17)
Лесно е да се провери, че разширението (2.16) се извършва по отношение на базисните функции  , които също са ортогонални на интервала
, които също са ортогонални на интервала  , т.е.
, т.е.

Изразът (2.16) е сложна формаРед на Фурие, който се простира до отрицателни честоти. Количества и  , където обозначава комплексно спрегнатата величина, се наричат комплексни амплитудиспектър защото е комплексна величина, от (2.15) следва, че
, където обозначава комплексно спрегнатата величина, се наричат комплексни амплитудиспектър защото е комплексна величина, от (2.15) следва, че
 И
И  .
.
Тогава съвкупността съставлява амплитудния спектър, а съвкупността съставлява фазовия спектър на сигнала.

На фиг. Фигура 2.4 показва спектрална диаграма на спектъра на последователността от правоъгълни импулси, обсъдени по-горе, представени от сложна серия на Фурие

Спектърът също има линеен характер, но за разлика от разгледаните по-рано спектри, той се определя както в областта на положителните, така и в областта на отрицателните честоти. Тъй като е четна функция на аргумента, спектралната диаграма е симетрична около нулата.
Въз основа на (2.15) можем да установим съответствие между коефициентите и разширението (2.3). защото
 И
И  ,
,
тогава в резултат получаваме
 . (2.18)
. (2.18)
Изрази (2.5) и (2.18) ви позволяват да намерите стойностите в практически изчисления.
Нека дадем геометрична интерпретация на сложната форма на реда на Фурие. Нека изберем k-тия компонент от спектъра на сигнала. В сложна форма k-тият компонент се описва с формулата
където и се определят от изрази (2.15).
В комплексната равнина всеки от членовете в (2.19) е представен като вектори на дължина  , завъртяни под ъгъл и спрямо реалната ос и въртящи се в противоположни посоки с честота (фиг. 2.5).
, завъртяни под ъгъл и спрямо реалната ос и въртящи се в противоположни посоки с честота (фиг. 2.5).
Очевидно сумата от тези вектори дава вектор, разположен върху реалната ос, чиято дължина е . Но този вектор съответства на хармоничната съставка


Що се отнася до проекциите на вектори върху въображаемата ос, тези проекции имат равни дължини, но противоположни посоки и сумата им е нула. Това означава, че сигналите, представени в сложна форма (2.16), всъщност са реални сигнали. С други думи, сложната форма на реда на Фурие е математическиабстракция, която е много удобна за решаване на редица проблеми на спектралния анализ. Следователно понякога се нарича спектърът, дефиниран от тригонометричния ред на Фурие физически спектър, а сложната форма на реда на Фурие е математически спектър.
И в заключение ще разгледаме въпроса за разпределението на енергията и мощността в спектъра на периодичен сигнал. За да направим това, използваме равенството на Парсевал (1.42). Когато сигналът се разшири в тригонометричен ред на Фурие, изразът (1.42) приема формата
 .
.
DC енергия
 ,
,
и енергията на k-тия хармоник
 .
.
Тогава енергията на сигнала
 . (2.20)
. (2.20)
защото средна мощност на сигнала
 ,
,
тогава като се вземе предвид (2.18)
 . (2.21)
. (2.21)
Когато сигналът се разшири в сложен ред на Фурие, изразът (1.42) приема формата
 ,
,
Където  - енергия на k-тия хармоник.
- енергия на k-тия хармоник.
Енергията на сигнала в този случай
 ,
,
и средната му мощност
 .
.
От горните изрази следва, че енергията или средната мощност на k-тия спектрален компонент на математическия спектър е наполовина по-малка от енергията или мощността на съответния спектрален компонент на физическия спектър. Това се дължи на факта, че физическият спектър е разпределен по равно между математическия спектър.
| -τ и /2 |
| τ и /2 |
| T |
| T |
| U 0 |
| S(t) |
Задача No1, група RI – 210701
Спектралното представяне на времеви функции се използва широко в теорията на комуникацията. За теоретични и експериментални изследвания на характеристиките на електрическите вериги и предаването на съобщения по комуникационни канали се използват различни видове сигнали: хармонични трептения, постоянни нива на напрежение, последователности от правоъгълни и радиоимпулси и др. Изчислителните сигнали под формата на Единичната функция играе особено важна роля в теоретичните изследвания на електрическите вериги и импулсната функция (функция на Дирак). Нека определим спектрите на най-често срещаните типични сигнали.
11.1 Спектър на последователност от правоъгълни импулси
Нека има периодична последователност от правоъгълни импулси с период T, продължителност на импулса t и амплитуда A. Аналитичният израз на функцията, описваща импулса върху сегмента, има формата
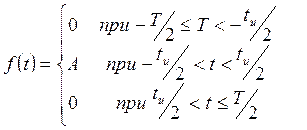 (11.1)
(11.1)
Графика на периодична импулсна последователност е показана на Фигура 11.1.

Фигура 11.1
Тази функция е четна, тъй като нейната графика е симетрична спрямо ординатата. След това коефициентите на Фурие на тези функции се изчисляват по формулите (KFT2), където .

Числото представлява средната стойност на функцията за период и се нарича постоянен компонент. Честотата се нарича основна или първа хармонична, а k честотите се наричат висши хармоници, където k = 2,3,4,...
Нека построим амплитудния спектър на разглежданата последователност от правоъгълни импулси. Тъй като функцията е периодична, нейният амплитуден спектър е начертан. Нека означим с разстоянието между всички съседни хармоници. Очевидно е равно на . Амплитудата на k-тия хармоник съгласно (11.2) има формата
 (11.3)
(11.3)
Нека намерим връзката между периода T и продължителността на импулса, при която амплитудата на k-тия хармоник става нула.
A 2 ≈32V, A 3 ≈15V, A 4 ≈0, A 5 ≈6,36V, A 6 ≈10,5V, A 7 ≈6,36V, A 8 ≈0, A 9 ≈4,95V, A 10 ≈6,37V.
Амплитудният спектър, получен в резултат на изчислението, е показан на фигура 11.2.

Фигура 11.2
Такъв спектър се нарича линеен или дискретен спектър.
Спектрите за q=8 и q=16 бяха изчислени и начертани по подобен начин. Те са показани съответно на фигури 11.3 и 11.4.

Фигура 11.3

Фигура 11.4
От фигурата може да се види, че колкото по-голям е коефициентът на запълване на правоъгълните импулси, толкова по-малка е амплитудата на първия хармоник, но толкова по-бавно намалява спектърът.
11.2 Спектър на единичен правоъгълен импулс
Нека разгледаме Ф (11.1) за случая, когато T→∞, т.е. периодична последователност от импулси се изражда в единичен правоъгълен импулс с продължителност t u.
Аналитичният израз за този импулс ще бъде написан като:

Графиката на тази функция е показана на фигура 11.5.

Фигура 11.5
В този случай честотата на първия хармоник и разстоянието между хармониците стават равни на 0, следователно спектърът се превръща от дискретен в непрекъснат, състоящ се от безкрайно голям брой спектрални линии, разположени на безкрайно малки разстояния една от друга. Такъв спектър се нарича непрекъснат. Това води до най-важното правило: периодичните сигнали генерират дискретни спектри, а непериодичните сигнали генерират непрекъснати спектри.
Спектърът на правоъгълен единичен импулс може да бъде намерен директно от директното преобразуване на Фурие (10.1)
Спектрален анализ на периодични сигнали
Както е известно, всеки сигнал S(t), описан от периодична функция на времето, която удовлетворява условията на Дирихле (моделите на реални сигнали ги удовлетворяват), може да бъде представен като сума от хармонични трептения, наречени ред на Фурие:
където е средната стойност на сигнала за периода или постоянната компонента на сигнала;

Коефициенти на ред на Фурие;
Основна честота (първа хармонична честота); n=1,2,3,...
Наборът от стойности An и n (или когато е разширен в синусоидални функции n) се нарича спектър на периодична функция. Хармоничните амплитуди An характеризират амплитудния спектър, а началните фази n (или "n) характеризират фазовия спектър.
По този начин спектърът на периодичен сигнал се представя като постоянен компонент и безкраен брой хармонични трептения (синус или косинус) със съответните амплитуди и начални фази. Всички хармонични честоти са кратни на основната честота. Това означава, че ако периодичен сигнал следва честота от например 1 kHz, тогава неговият спектър може да съдържа само честоти от 0 kHz, 1 kHz, 2 kHz и т.н. Спектърът на такъв периодичен сигнал не може да съдържа например честоти от 1,5 kHz или 1,2 kHz.
На фиг. 1. Показани са амплитудните и фазовите спектри на определен периодичен сигнал. Всяка хармонична съставка се изобразява като вертикални сегменти, чиито дължини (в някакъв мащаб) са равни на нейната амплитуда и фаза. Както можете да видите, спектърът на периодичен сигнал е дискретен или, както се казва, очертан.
За да се опростят изчисленията, вместо тригонометричната форма на записване на реда на Фурие, те често използват сложна форма на писане, чиито коефициенти комбинират коефициентите An и n:

Наборът от комплексни амплитуди n се нарича комплексен спектър на периодичен сигнал.
Изчисляването на сигналните спектри в сложната област е много по-просто, тъй като не е необходимо да се разглеждат отделно коефициентите и тригонометричната форма за записване на реда на Фурие.
Спектър на периодична последователност от правоъгълни импулси
Преди да разгледаме спектъра на периодична последователност от правоъгълни импулси, нека разгледаме параметрите на тези импулси.
Параметрите на единичен импулс са амплитуда, продължителност на импулса, време на нарастване, продължителност на спадане и спад на плоския връх (разцепване).
Амплитудата на импулса Um се измерва във волтове.
Продължителността на импулса се измерва в основата, на нива от 0,1 Um или 0,5 Um. В последния случай продължителността на импулса се нарича активна. Продължителността на импулса се измерва в единици време.
Продължителността на фронта tf и падането tс се измерва или на ниво 0 - Um, или на ниво (0,1-0,9) Um. В последния случай продължителността на фронта и спада се нарича активна.
Цепителността с плосък връх се характеризира с коефициент на цепителност? = ?u/Um,
където?u е стойността на чипа; Um - амплитуда на импулса.
Параметрите на импулсната серия са период на повторение T, честота на повторение f, работен цикъл Q, работен цикъл, средни стойности на напрежението Uav и средна стойност на мощността Pav.
Период на повторение T = ti +tp, където T е периодът, ti е продължителността на импулса, tp е продължителността на паузата. T, tи и tп се измерват в единици време.
Честотата на повторение f = 1/T се измерва в херци и т.н.
Коефициентът на запълване Q = T/ti е безразмерна величина.
Коефициентът на запълване = ti/T е безразмерна величина.
Средно напрежение

Да преминем към разглеждане на амплитудния и фазов спектър на сигнала под формата на периодична последователност от правоъгълни импулси с продължителност и амплитуда Um, следвани от период T (фиг. 2).

Нека разгледаме случая, когато средата на импулса е началото на отброяването на времето. Тогава сигналът за периода се описва с израза

Комплексни амплитуди на хармоничните компоненти.
Функцията е знакопроменлива и променя знака си на противоположен, когато аргументът n1 се промени със сумата?



където k е поредният номер на интервала на честотната скала, броено от нулева честота.
По този начин хармоничните амплитуди, включително DC компонента, се определят от израза:

а фазите - по израза =1, 2,3,...
Функцията характеризира промяната в амплитудния спектър на сигнала в зависимост от честотата. Той изчезва за стойности на неговия аргумент, които са кратни. От това следва, че хармониците с номер n = , където = 1,2,3,... ще имат нулеви амплитуди, т.е. отсъства от спектъра.
Както знаете, съотношението се нарича работен цикъл на импулсната последователност. По този начин в спектъра на разглежданата последователност няма да има хармоници, чиито номера са кратни на работния цикъл.
Ако началото на отброяването на времето е свързано с началото на импулса, тогава амплитудният спектър ще остане непроменен, а фазите на хармониците, в съответствие със свойството на преобразуването на Фурие, ще получат допълнително фазово изместване nп1ф/2 . Като резултат
Изразите за тригонометричната форма на запис на серията на Фурие при отчитане на времето съответно от средата и началото на импулса имат формата:


На фиг. 3. Показани са амплитудните и фазовите спектри на разглежданата последователност от правоъгълни импулси с работен цикъл два.
Фазовите спектри са показани съответно при отчитане на времето от средата и началото на импулса. Пунктираните линии в амплитудните спектри характеризират поведението на модула на спектралната плътност на единичен импулс.
Изразът за стойностите на амплитудите и фазите на хармониците може лесно да се получи във форма, удобна за изчисления. И така, когато броим времето от средата на импулса за работен цикъл, равен на две, имаме
В този израз
| |
функция sinc, както е показано на фиг. 2.6, достига максимум (единство) при y = 0 и клони към нула при при® ±¥, осцилиращи с постепенно намаляваща амплитуда. Преминава през нула в точки при= ±1, ±2, …. На фиг. 2.7, Акато функция на съотношението п/т 0 показва амплитудния спектър на импулсната последователност | с n|, а на фиг. 2.7, bе показан фазовият спектър q н. Трябва да се отбележи, че положителните и отрицателните честоти на двупосочен спектър са полезен начин за математическо изразяване на спектъра; Очевидно е, че в реални условия могат да се възпроизвеждат само положителни честоти.
Поведение
Идеалната периодична импулсна поредица включва всички хармоници, които са кратни на естествената честота. В комуникационните системи често се приема, че значителна част от мощността или енергията на теснолентовия сигнал възниква при честоти от нула до първата нула на амплитудния спектър (фиг. 2.7, А). Така, като мярка честотна лентаимпулсна последователност, често се използва стойността 1/ T(Където T -продължителност на импулса). Имайте предвид, че честотната лента е обратно пропорционална на продължителността на импулса; Колкото по-къси са импулсите, толкова по-широка е свързаната с тях лента. Обърнете внимание също, че разстоянието между спектралните линии D f= 1/T 0 е обратно пропорционална на периода на импулса; С увеличаването на периода линиите са разположени по-близо една до друга.
Таблица 2.1. Изображения на Фурие
| х(T) | х(f) |
| д( T) | |
| д( f) | |
| cos 2 стр f 0 T | /2 |
| грях 2 стр f 0 T | /2 |
| д( T - T 0) | |
| д( f - f 0) | |
| , а>0 | |
 | |
| | |
| опит (- при)u(T), а>0 | |
| прав( T/ T) | T sinc fT |
| У sinc Wt | прав( f / У) |
 |
 sinc х =
sinc х =
Таблица 2.2 Свойства на преобразуването на Фуриее)