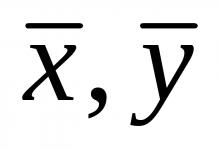В цялата предишна презентация ние определихме напречните размери на пръчките от условията сила.Въпреки това, разрушаването на пръта може да се случи не само защото ще бъде нарушена здравината, но и защото прътът няма да запази формата, която му е дадена от дизайнера; в този случай естеството на състоянието на напрежение в пръта също ще се промени.
Повечето типичен примере работата на пръчка, компресирана от сили Р. Досега за проверка на силата имахме условието
Това условие предполага, че пръчката работи в аксиална компресия през цялото време, чак до разрушаване. Вече най-простият опитпоказва, че не винаги е възможно да се разруши прът чрез довеждане на напреженията на натиск до границата на провлачване или до границата на якост на материала.
Ако подложим тънка дървена линийка на надлъжна компресия, тя може да се счупи и огъне; Преди счупването силите на натиск, при които линийката ще се срути, ще бъдат значително по-малки от тези, които биха причинили напрежение, равно на якостта на опън на материала по време на просто натиск. Разрушаването на линийката ще настъпи, защото тя няма да може да запази дадената й форма на прав, компресиран прът, а ще се огъне, което ще доведе до появата на огъващи моменти от натискни сили Ри следователно допълнителни напрежения от огъване; владетелят ще загуби устойчивост.
Следователно, за надеждна работа на една конструкция, не е достатъчно тя да бъде издръжлива; необходимо е всички негови елементи да бъдат стабилен: те трябва под действието на натоварвания да се деформират в такива граници, че естеството на тяхната работа да остане непроменено. Следователно, в редица случаи, по-специално за компресирани пръти, в допълнение към изпитването за якост е необходимо и изпитване за стабилност. За да се извърши тази проверка, е необходимо да се запознаете по-добре с условията, при които се нарушава стабилността на праволинейната форма на компресирания прът.
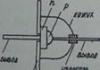
Фиг. 1.Изчислителна схема
Нека вземем прът, който е доста дълъг в сравнение с напречните си размери, шарнирно закрепен към опорите (фиг. 1), и го натоварваме отгоре с централна сила Р, като постепенно се увеличава. Ще видим, че докато силата Ре сравнително малък, пръчката ще поддържа права форма. Когато се опитвате да го отклоните настрани, например чрез прилагане на краткотрайна хоризонтална сила, след поредица от трептения той ще се върне към първоначалната си праволинейна форма веднага щом допълнителната сила, причинила отклонението, бъде премахната.
С постепенно увеличаване на силата Рпрътът ще се връща все по-бавно в първоначалното си положение при проверка на неговата стабилност; най-накрая можете да донесете силата Рдо такава стойност, при която прътът, след леко отклонение настрани, вече няма да се изправи, а ще остане извит. Ако ние, без да премахваме силата Р, изправете пръчката; като правило тя вече няма да може да поддържа права форма. С други думи, при тази стойност на силата Р, Наречен критичен, ще имаме състояние на равновесие, когато се изключи вероятността прътът да запази дадената си праволинейна форма).
Преход към стойност на критичната сила Рсе случва внезапно; Веднага след като намалим силата на натиск съвсем леко в сравнение с нейната критична стойност, праволинейната форма на равновесие отново става стабилна.
От друга страна, с много малък излишък на сила на натиск Рнеговата критична стойност, праволинейната форма на пръта е направена изключително нестабилен; в този случай малък ексцентрицитет на приложената сила и хетерогенността на материала по напречното сечение са достатъчни, за да може прътът да се огъне и не само да не се върне към предишната си форма, но продължава да се огъва под въздействието на огъващи моменти, които увеличаване по време на кривина; процесът на изкривяване завършва или с постигането на напълно нова (стабилна) форма на равновесие, или с разрушаване.
Въз основа на това трябва практически да считаме критичната стойност на силата на натиск за еквивалентна на натоварването, което „унищожава“ компресирания прът, премахвайки го (и свързаната с него структура) от нормалните работни условия. Разбира се, трябва да се помни, че „унищожаването“ на пръта чрез натоварване, надвишаващо критичното, може да се случи при необходимото условие за безпрепятствено увеличаване на кривината на пръта; следователно, ако по време на странично изкривяване прътът срещне странична опора, която ограничава по-нататъшното му изкривяване, тогава може да не настъпи разрушаване.
Обикновено такава възможност е изключение; следователно на практика критичната сила на натиск трябва да се счита за най-ниската граница на "разрушителната" сила на пръта.

Фиг.2.Аналогия на концепцията за устойчивост от механиката твърдо
Явлението загуба на стабилност по време на компресия може да се илюстрира по аналогия със следния пример от механиката на твърдото тяло (фиг. 2). Ще търкаляме цилиндъра върху наклонена равнина аб, която след това се превръща в къса хоризонтална платформа bси наклонена равнина обратна посока CD. Докато повдигаме цилиндъра по равнината аб, поддържайки го със стоп, перпендикулярен на наклонената равнина, той ще бъде в състояние на стабилно равновесие; на сайта bсравновесието му става безразлично; Веднага щом поставим цилиндъра в точка c, неговото равновесие ще стане нестабилно; при най-малкото натискане надясно цилиндърът ще започне да се движи надолу.
Физическата картина на загубата на стабилност на компресиран прът, описана по-горе, може лесно да се реализира в действителност във всяка механична лаборатория, като се използва много елементарна настройка. Това описание не е някаква теоретична, идеализирана схема, а отразява поведението на реален прът под действието на натискни сили.
Загубата на стабилност на праволинейната форма на компресиран прът понякога се нарича "надлъжно огъване", тъй като води до значителна кривина на пръта под действието на надлъжни сили. За изпитване на устойчивост и до днес се е запазил терминът „тест на надлъжно огъване“, който е условен, тъй като тук не говорим за тест на огъване, а за проверка на устойчивостта на праволинейната форма на пръта.
След като установихме концепцията за критична сила като „разрушително“ натоварване, което премахва пръта от условията на нормалната му работа, можем лесно да създадем условие за тестване на стабилност, подобно на състоянието на якост.
Критичната сила причинява напрежение в компресирания прът, наречено „критично напрежение“ и обозначено с буквата . Критичните напрежения са опасни напрежения за компресиран прът. Следователно, за да се осигури стабилността на праволинейната форма на пръта, компресиран от сили Р, е необходимо да се добави условието за стабилност към условието за якост:
където допустимото напрежение за устойчивост, равно на критичното, разделено на коефициента на безопасност за устойчивост, т.е.
За да можем да извършим проверка на стабилността, трябва да покажем как да определим и как да изберем коефициента на безопасност.
Формула на Ойлер за определяне на критичната сила.
За да се намерят критичните напрежения, е необходимо да се изчисли критичната сила, т.е. най-малката аксиална сила на натиск, способна да поддържа леко извит сгъстен прът в равновесие.
Този проблем е решен за първи път от академика на Петербургската академия на науките Л. Ойлер през 1744 г.
Обърнете внимание, че самата формулировка на проблема е различна от тази във всички разгледани преди това раздели на курса. Ако по-рано определихме деформацията на пръта при определени външни натоварвания, тогава тук поставяме обратна задача: като се има предвид кривината на оста на компресирания прът, е необходимо да се определи при каква стойност на аксиалната сила на натиск Ртакова изкривяване е възможно.
Нека разгледаме прав прът с постоянно напречно сечение, шарнирно поддържан в краищата; една от опорите позволява надлъжно движение на съответния край на пръта (фиг. 3). Пренебрегваме собственото тегло на пръта.

Фиг.3.Схема за изчисление в "проблема на Ойлер"
Нека натоварим пръта с централно приложени надлъжни сили на натиск и му придадем много лека кривина в равнината на най-малка твърдост; прътът се поддържа в извито състояние, което е възможно поради .
Приема се, че деформацията на огъване на пръта е много малка, така че за решаване на поставения проблем може да се използва приблизителното диференциално уравнение за извитата ос на пръта. Чрез избор на началото на координатите в точката Аи посоката на координатните оси, както е показано на фиг. 3, имаме:
|
Да вземем разрез от разстояние хот произхода; ординатата на кривата ос в този участък ще бъде при, а огъващият момент е равен на
Според оригиналната схема огъващият момент се оказва отрицателен, но ординатите за избраната посока на оста са присе оказват положителни. (Ако прътът беше огънат с изпъкналост надолу, тогава моментът би бил положителен и приотрицателен и .)
Току-що даденото диференциално уравнение приема формата:
разделяйки двете страни на уравнението на EJи обозначавайки дробта чрез, ние го привеждаме във формата:
Общият интеграл на това уравнение има формата.
Иркутск Държавен университеткомуникационни линии
Лабораторна работа №16
по дисциплина "Съпротивление на материалите"
ЕКСПЕРИМЕНТАЛНО ОПРЕДЕЛЯНЕ НА КРИТИЧНИТЕ СИЛИ
С НАДЪЛЖНО ОГЪВАНЕ
Катедра PM
Лабораторна работа №16
Експериментално определяне на критичните сили при надлъжно огъване
Цел на работата:изследване на явлението загуба на стабилност на компресиран стоманен прът в еластичен
етапи. Експериментално определяне на стойностите на критичните компресирани натоварвания
пръчки при по различни начиниконсолидация и съпоставка с теоретичните
стойности.
Не е достатъчно да се тестват компресирани пръти за якост според известно състояние:
 ,
,
където [σ] е допустимото напрежение за материала на пръта, П – сила на натиск, Е – площ на напречното сечение.
IN практически дейностиИнженерите се занимават с гъвкави пръти, подложени на компресия, тънки компресирани плочи, тънкостенни конструкции, чийто отказ се дължи не на загуба на носеща способност, а на загуба на стабилност.
Загубата на стабилност се отнася до загубата на първоначалната форма на баланс.
Якостта на материалите разглежда стабилността на структурните елементи, работещи при компресия.
Помислете за дълъг тънък прът (фиг. 1), натоварен с аксиална сила на натиск П .
П< П кр П > Пкр

Ориз. 1.Прът, натоварен с аксиална сила на натиск П .
При ниски стойности на сила Епръчката се свива, докато остава права. Освен това, ако прътът се отклони от това положение с малък напречен товар, той ще се огъне, но когато се отстрани, прътът се връща в изправено състояние. Това означава, че за дадена сила П праволинейната форма на равновесие на пръта е стабилна.
Ако продължите да увеличавате силата на натиск П , то при определена стойност праволинейната форма на равновесието става неустойчива и а нова формаравновесие на пръта - криволинейно (фиг. 1, б) . Поради огъването на пръта, в неговите секции ще се появи момент на огъване, което ще причини допълнително напрежение и прътът може внезапно да се провали.
Кривината на дълъг прът, компресиран от надлъжна сила, се нарича надлъжно огъване .
Най-висока стойностсе нарича сила на натиск, при която праволинейната форма на равновесие на пръта е стабилна критичен - П кр.
При достигане на критичното натоварване настъпва рязка качествена промяна в изходната форма на равновесие, което води до разрушаване на конструкцията. Следователно критичната сила се счита за натоварване при скъсване.
Формули на Ойлер и Ясински
Проблемът за определяне на критичната сила на компресиран прът е решен за първи път от Л. Ойлер, член на Академията на науките в Санкт Петербург, през 1744 г. Формулата на Ойлер има формата
 (1)
(1)
Където д – модул на еластичност на материала на пръта; Джмин- най-малкият инерционен момент на напречното сечение на пръта (тъй като кривината на пръта по време на загуба на стабилност възниква в равнината на най-малка твърдост, т.е. напречните сечения на пръта се въртят около оста, спрямо която моментът на инерцията е минимална, т.е. или около оста х , или около оста г );
(μ· л ) – намалена дължина на пръта, това е произведението на дължината на пръта л чрез коефициента μ, който зависи от методите за закрепване на краищата на пръта.
Коефициент μ Наречен фактор на намаляване на дължината ; стойността му за най-често срещаните случаи на закрепване на краищата на пръта е показана на фиг. 2:
А- двата края на пръта са шарнирно закрепени и могат да се приближат един до друг;
b- единият край е здраво захванат, другият е свободен;
V- единият край е шарнирен, вторият е с "напречно плаващо уплътнение";
Ж - единият край е здраво захванат, вторият има „напречно плаващо уплътнение“;
д- единият край е фиксиран неподвижно, от другата има шарнирна и подвижна опора;
д- двата края са здраво притиснати, но могат да се приближат един до друг.
От тези примери става ясно, че коеф μ е реципрочната стойност на броя на полувълните на еластичната линия на пръта при загуба на стабилност.

Ориз. 2.Коефициент μ за най-често
случаи на закрепване на краищата на пръта.
Нормалното напрежение в напречното сечение на компресиран прът, съответстващо на критичната стойност на силата на натиск, също се нарича критично.
Нека го определим въз основа на формулата на Ойлер:
 (2)
(2)
Геометрични характеристики на сечението азмин, определена по формулата
Наречен радиус на въртене на сечението (спрямо оста c Джмин). За правоъгълно сечение

Като се вземе предвид (3), формула (2) ще приеме формата:
 (4)
(4)
Съотношението на намалената дължина на пръта към минималния радиус на въртене на неговото напречно сечение според предложението на професора от Санкт Петербургския институт на железопътните инженери F.S. Ясински (1856-1899) се нарича гъвкавост на пръта и се обозначава с буквата λ :
Тази безразмерна стойност отразява едновременно следните параметри: дължината на пръта, метода на неговото закрепване и характеристиките на напречното сечение.
Накрая, замествайки (5) във формула (4), получаваме
При извеждането на формулата на Ойлер се приема, че материалът на пръта е еластичен и следва закона на Хук. Следователно формулата на Ойлер може да се приложи само при напрежения, по-малки от границата на пропорционалност σ настолен компютър, тоест когато

Това условие определя границата на приложимост на формулата на Ойлер:
Количеството от дясната страна на това неравенство се нарича изключителна гъвкавост :

стойността му зависи от физичните и механичните свойства на материала на пръта.
За нисковъглеродна стомана чл. 3, за които σ настолен компютър= 200 MPa, д = 2· 10 5 MPa:
По същия начин можете да изчислите стойността на максималната гъвкавост за други материали: за чугун λ преди= 80, за бор λ преди = 110.
По този начин формулата на Ойлер е приложима за пръти, чиято гъвкавост е по-голяма или равна на крайната гъвкавост, т.е.
λ ≥ λ преди
Това трябва да се разбира по следния начин: ако гъвкавостта на пръта е по-голяма от максималната гъвкавост, тогава критичната сила трябва да се определи с помощта на формулата на Ойлер.
При λ < λ предиФормулата на Ойлер за пръти не е приложима. В тези случаи, когато гъвкавостта на прътите е по-малка от максималната, при изчисленията се използват емпирични стойности. Формулата на Ясински :
σ кр = а – b· λ , (7)
Където А И b - дефинирани емпиричнокоефициенти, които са постоянни за даден материал; те имат измерението на напрежението.
При някаква стойност на гъвкавост λ Онапрежение σ кр, изчислена по формула (7), става равна на пределното напрежение на натиск, т.е. границата на провлачване σ Tза пластмасови материали или якост на натиск σ слънце– за чупливи материали. Пръчки с ниска гъвкавост ( λ < λ О) не се разчитат на стабилност, а на здравина при проста компресия.
По този начин, в зависимост от гъвкавостта, изчисленията на стабилността на компресирани пръти се извършват по различен начин.
В конструкциите и конструкциите частите, които се използват широко, са относително дълги и тънки пръти, в които един или два размера на напречното сечение са малки в сравнение с дължината на пръта. Поведението на такива пръти под действието на аксиално натоварване на натиск се оказва коренно различно от това при компресиране на къси пръти: когато силата на натиск F достигне определена критична стойност, равна на Fcr, се оказва праволинейната форма на равновесие на дългия прът да е нестабилна, а при превишаване на Fcr пръчката започва интензивно да се огъва (издува). В същото време нов (моментен) равновесно състояниееластичната дълга става някаква нова вече криволинейна форма. Това явление се нарича загуба на стабилност.
Ориз. 37. Загуба на стабилност
Стабилността е способността на тялото да поддържа позиция или форма на равновесие при външни влияния.
Критичната сила (Fcr) е натоварване, превишаването на което води до загуба на стабилност на първоначалната форма (позиция) на тялото. Условие за стабилност:
Fmax ≤ Fcr, (25)
Стабилност на компресиран прът. Проблем на Ойлер.
При определяне на критичната сила, която причинява загуба на стабилност на компресиран прът, се приема, че прътът е идеално прав и силата F се прилага строго централно. Проблемът за критичното натоварване на компресиран прът, като се вземе предвид възможността за съществуването на две форми на равновесие при една и съща стойност на силата, е решен от Л. Ойлер през 1744 г.
Ориз. 38. Компресиран прът
Нека разгледаме прът, шарнирно поддържан в краищата, компресиран от надлъжна сила F. Да приемем, че по някаква причина прътът е получил леко изкривяване на оста си, в резултат на което в него се е появил момент на огъване M:
където y е отклонението на пръта в произволно сечение с координата x.
За да определите критичната сила, можете да използвате приблизителното диференциално уравнение на еластична линия:
![]() (26)
(26)
След извършване на трансформациите можете да видите, че критичната сила ще приеме минимална стойност при n = 1 (една полувълна на синусоида пасва по дължината на пръта) и J = Jmin (пръчката е огъната спрямо оста с най-малък инерционен момент)
![]() (27)
(27)
Този израз е формулата на Ойлер.
Зависимост на критичната сила от условията на фиксиране на пръта.
Формулата на Ойлер е получена за така наречения главен случай - при предположението, че прътът е шарнирно закрепен в краищата. На практика има и други случаи на фиксиране на пръта. В този случай е възможно да се получи формула за определяне на критичната сила за всеки от тези случаи чрез решаване, както в предходния параграф, на диференциалното уравнение на кривата ос на гредата със съответните гранични условия. Но можете да използвате и по-проста техника, ако помните, че в случай на загуба на стабилност една половин вълна от синусоида трябва да пасне по дължината на пръта.
Нека разгледаме някои типични случаи на закрепване на пръчка в краищата и да получим обща формула за различни видове закрепване.



Ориз. 39. Различни случаи на фиксиране на пръта
Обща формулаОйлер:
 (28)
(28)
където μ·l = l pr – приведена дължина на пръта; l – действителната дължина на пръта; μ е намаленият коефициент на дължина, показващ колко пъти трябва да се промени дължината на пръта, така че критичната сила за този прът да стане равна на критичната сила за просто поддържана греда. (Друга интерпретация на намаления коефициент на дължина: μ показва върху каква част от дължината на пръта за даден тип закрепване пасва една полувълна на синусоида по време на изкълчване.)
Така условието за стабилност най-накрая ще приеме формата
![]() (29)
(29)
Нека разгледаме два вида изчисления за стабилността на компресирани пръти - тестване и проектиране.
Изчисление за проверка
Процедурата за проверка на стабилността е следната:
– въз основа на известните размери и форма на напречното сечение и условията за закрепване на пръта, изчисляваме гъвкавостта;
– използвайки референтната таблица, намираме коефициента на намаляване на допустимото напрежение, след което определяме допустимото напрежение за стабилност;
– сравняваме максималното напрежение с допустимото напрежение за стабилност.
Проектно изчисление
По време на проектното изчисление (избор на напречно сечение за дадено натоварване), формулата за изчисление съдържа две неизвестни величини - желаната площ на напречното сечение A и неизвестния коефициент φ (тъй като φ зависи от гъвкавостта на пръта и следователно от непознатата област А). Следователно при избора на напречно сечение обикновено е необходимо да се използва методът на последователните приближения.
Нека определим критичната сила за централно компресиран прът, шарнирно поддържан в краищата (фиг. 13.4). При ниски стойности на сила Роста на пръта остава права и в сеченията му възникват централни напрежения на натиск o = P/F.При критична стойност на силата P = P става възможна извита форма на равновесие на пръта.
Получава се надлъжен завой. Моментът на огъване в произволно сечение x на пръта е равен на
Важно е да се отбележи, че огъващият момент се определя за деформираното състояние на пръта.
Ако приемем, че напреженията на огъване, възникващи в напречните сечения на пръта от действието на критичната сила, не надвишават границата на пропорционалност на материала около pc и деформациите на пръта са малки, тогава можем да използваме приблизителната разлика уравнение за извитата ос на пръта (виж § 9.2)
Чрез въвеждане на обозначението
Вместо (13.2) получаваме следното уравнение:
Общото решение на това уравнение е
Това решение съдържа три неизвестни: интеграционни константи Cj, C 2 и параметъра Да се,тъй като величината на критичната сила също е неизвестна. За да се определят тези три количества, има само две гранични условия: u(0) = 0, v(l) = 0. От първото гранично условие следва, че C 2 = 0, а от второто получаваме
От това равенство следва, че или C (= 0 или грях kl = 0. При C, = 0, деформациите във всички сечения на пръта са равни на нула, което противоречи на първоначалното допускане на задачата. Във втория случай kl = pk,Където П -произволно цяло число. Като вземем предвид това, използвайки формули (13.3) и (13.5), получаваме

Разглежданият проблем е проблем със собствените стойности. Намерени числа Да се = бр./1са наречени собствени номера,и съответните функции са собствени функции.
Както се вижда от (13.7), в зависимост от числото Псилата на натиск P (i), при която прътът е в огънато състояние, теоретично може да приеме редица стойности. В този случай, съгласно (13.8), прътът се огъва Пполувълни на синусоида (фиг. 13.5).
Минималната стойност на силата ще бъде при П = 1:
Тази сила се нарича първа критична сила.При което kl = kа извитата ос на пръта представлява една полувълна на синусоида (фиг. 13.5, А):
Където C(1)=/ - отклонение в средата на дължината на пръта, което следва от (13.8) при П= 1 тях = 1/2.
Формула (13.9) е получена от Леонхард Ойлер и се нарича формула на Ойлер за критичната сила.
Всички форми на равновесие (фиг. 13.5), с изключение на първата (П= 1), са нестабилни и следователно не представляват практически интерес. Равновесни форми съответстващи П - 2, 3, ..., ще бъдат стабилни, ако в точките на огъване на еластичната линия (точки C и C" на фиг. 13.5, б, в)въведете допълнителни опори за панти.

Полученото решение има две характеристики. Първо, решение (13.10) не е уникално, тъй като произволната константа Cj (1) =/ остава недефинирана, въпреки използването на всички гранични условия. В резултат на това отклоненията бяха определени с точност до постоянен фактор. Второ, това решение не дава възможност да се опише състоянието на пръта при P > P кр.От (13.6) следва, че когато P = P крпръчката може да има извита осигурена равновесна форма kl = k.Ако Р > R cr,Че kl F p,и тогава трябва да е Cj (1) = 0. Това означава, че v = 0, тоест прътът след кривина при P = P кротново придобива праволинейна форма, когато R > R.Очевидно това противоречи на физическите концепции за огъване на пръта.
Тези особености се дължат на факта, че изразът (13.1) за огъващия момент и диференциалното уравнение (13.2) са получени за деформираното състояние на пръта, докато при задаване на граничното условие в края х= / аксиално движение и втози край (фиг. 13.6) поради огъване не беше взет предвид. Наистина, ако пренебрегнем скъсяването на пръта поради централна компресия, тогава не е трудно да си представим, че отклоненията на пръта ще имат доста определени стойности, ако зададем стойността и c.
От това разсъждение става очевидно, че за да се определи зависимостта на деформациите от големината на силата на натиск Рнеобходимо вместо гранично условие v(l)= 0 използвайте прецизирано гранично условие v(l - и v) = 0. Установено е, че ако силата превиши критичната стойност само с 1+2%, деформациите стават доста големи и е необходимо да се използва точно нелинейно диференциално уравнение на изкълчване
Това уравнение се различава от приблизителното уравнение (13.4) в първия член, който е точен израз за кривината на извитата ос на пръта (виж § 9.2).
Решението на уравнение (13.11) е доста сложно и се изразява чрез пълен елиптичен интеграл от първи род.
Да разгледаме прът с дължина /, чийто един край е неподвижно фиксиран, а централна натискна сила се прилага към другия свободен край Е(фиг. 15.8).
Ориз. 15.8.
Общото решение на задачата, написано под формата на формула (15.15), в този случай остава валидно. Що се отнася до граничните условия, те ще бъдат записани в следната форма:
Желаното решение може да се намери и по друг начин. Нека условно разширим пръта вдясно от захванатата опора за дължина / симетрично на лявата страна и след това вместо гранични условия (15.21) получаваме нови условия:
Така новият проблем всъщност съвпада с проблема на Ойлер, разгледан по-горе. Единствената разлика е, че в крайния резултат (15.20) дължината / трябва да бъде заменена с 21:
Формулата на Ойлер може да се обобщи и за други случаи на закрепване на краищата на пръта. За да направите това в формула за изчислениеОйлер въвежда корекционен коефициент p, наречен фактор на намаляване на дължинатапрът:
Коефициентът е числено равен на реципрочната стойност на броя на полувълните на синусоида, които пасват по кривата ос на пръта. На фиг. 15.9 представени различни видовезакрепвания на краищата на пръта и съответните коефициенти на намаляване на дължината.
Може да се покаже, че за първите три пръта, показани на фиг. 15.9, А - c, стойностите на намаления коефициент на дължина са точни. Що се отнася до четвъртата задача, за нея стойността на намалената дължина се определя приблизително. Нека разгледаме проблема за определяне на p за този случай (фиг. 15.9, Ж).
Уравнението за деформираната ос на пръта има вида
Тук Р-големината на хоризонталната сила на реакция на горната опора.

Ориз. 15.9.
След преобразуване на уравнение (15.25), като се вземе предвид формула (15.13), получаваме
Уравнение (15.26), за разлика от уравнение (15.14), е нехомогенно. Неговата общо решениеще бъде записано по същия начин като общото решение на съответното хомогенно уравнение (15.14). Конкретно решение има формата
Така решението на уравнение (15.25) ще бъде записано във формата
В този разтвор количеството Риграе ролята на трета неизвестна константа и следователно за решаването на този проблем е необходимо да се формулира трето гранично условие:
Използвайки гранични условия, получаваме система от три нелинейни уравнения


Разширявайки детерминантата, стигаме до следното нелинейно уравнение:
Решението на нелинейното уравнение (15.29) може да се получи както числено, така и графично. За по-голяма яснота ще изберем втория метод на решение. Нека изградим графики на следните функции: при= tg kl, y = kl(фиг. 15.10).

Ориз. 15.10.Функционални графикипри= tgkl, y = kl
Пресечна точка на графики СЪСсъответства на коренната стойност кл~ 4.5, откъдето

Формулата за критичната сила включва главния централен момент на инерция спрямо оста Оз-/ Ю1. = тъй като направихме предположението преди време, че прътът губи стабилност и се огъва в посока, перпендикулярна на оста оВъпреки това, както вече беше отбелязано, ако условията за закрепване на опорите позволяват прътът да се деформира във всяка посока с еднаква вероятност, тогава прътът ще загуби стабилност в посоката, в която инерционният момент на неговото напречно сечение има минимална стойност от 7 мин.
Ако условията на закрепване са по-сложни, тогава е необходим допълнителен анализ за оценка на критичната сила. Например, помислете за прът (фиг. 15.11), чиято лява опора е твърдо вградена. Що се отнася до дясната опора, тук са посочени условията за подвижно вграждане, позволяващи движения и завъртания в равнината xyи забраняването им в самолета zx.Напречното сечение на пръта е правоъгълно със съотношение на страните N = 2IN.

Ориз. 15.11.
Закрепване на пръта в равнината xyсъответства на коефициента на намаляване на дължината p = 2 (виж фиг. 15.8), а в равнината xz- p = 0.5 (виж Фиг. 15.9, А).
Нека изчислим критичните сили при предположението, че ще настъпи загуба на стабилност: 1) в равнината xyи 2) в равнината xz:

Сравнявайки стойностите, заключаваме: в равнината ще настъпи загуба на стабилност xy, тъй като тази опция съответства на по-ниска стойност на критичната сила.