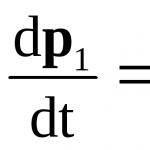Термодинамична система, колектив и нейните състояния. Ансамбъл метод. Ентропия и вероятност. Каноничен ансамбъл на Гибс. Канонично разпределение. Фактор на Гибс. Вероятности, свободна енергия и разделителна функция.
Система и подсистеми. Общи свойствастатистически суми. Статистическа сума на пробна частица и колектив.
Идеален газ. Разпределение на Болцман. Коефициент на Болцман. Квантови състояния и дискретни нива на прости молекулярни движения. Статистическа тежест на нивото (дегенерация). Суми по нива и суми по държави.
Локализирани и делокализирани системи. Транслационен сбор от състояния, неразличимост на частиците, стандартен обем. Ротационна сума по нива двуатомна молекула, ориентационна неразличимост и число на симетрия. Разделителни функции за една и няколко степени на свобода на въртене. Осцилаторна делителна функция в хармонично приближение. Корекция на статистически суми от прости движения. Нулево ниво на вибрация, скала на молекулярната енергия и молекулярна сума от състояния.
Свободна енергия A и статистически формули за термодинамични функции: ентропия S, налягане p, вътрешна енергия U, енталпия H, енергия на Гибс G, химичен потенциал m. Химическа реакцияи равновесната константа Kp в системата от идеални газове.
1. Въведение. Кратко напомняне за основите на термодинамиката.
...Термодинамичните аргументи и определените с тяхна помощ функции на състоянието е удобно да се представят като единен масив от взаимосвързани променливи. Този метод е предложен от Гибс. Така че, да речем, ентропията, която по дефиниция е функция на състоянието, се премества в категорията на една от двете естествени калорични променливи, допълвайки температурата в това си качество. И ако във всички калорични процеси температурата изглежда като интензивна (силова) променлива, то ентропията придобива статуса на екстензивна променлива - топлинна координата.
Този масив винаги може да бъде допълнен с нови функции на състоянието или, ако е необходимо, уравнения на състоянието, свързващи аргументите. Броят на аргументите, необходими за цялостно термодинамично описание на системата, се нарича брой степени на свобода. Тя се определя от фундаментални съображения на термодинамиката и може да бъде намалена поради различни уравнениякомуникации.
В такъв единичен масив ролите на аргументите и функциите на състоянието могат да бъдат разменени. Тази техника се използва широко в математиката при конструиране на обратни и неявни функции. Целта на такива логически и математически техники (доста фини) е да се постигне максимална компактност и хармоничност на теоретичната схема.
2. Характерни функции. Масови диференциални уравнения.
Удобно е масивът от променливи p, V, T да се допълни с функцията на състоянието S. Между тях има две уравнения на връзка. Една от тях се изразява под формата на постулирана взаимозависимост на променливите f(p,V,T) =0. Когато се говори за „уравнение на състоянието“, най-често се има предвид именно тази зависимост. Всяка функция на състоянието обаче съответства на ново уравнение на състоянието. Ентропията по дефиниция е функция на състоянието, т.е. S=S(p,V,T). Следователно има две връзки между четирите променливи и само две могат да бъдат идентифицирани като независими термодинамични аргументи, т.е. За цялостно термодинамично описание на системата са достатъчни само две степени на свобода. Ако този масив от променливи се допълни нова функциясъстояние, тогава заедно с новата променлива се появява друго уравнение на свързване и следователно броят на степените на свобода няма да се увеличи.
В исторически план първата държавна функция е вътрешната енергия. Следователно с негово участие можете да формирате първоначалния масив от променливи:
Масивът от уравнения за свързване в този случай съдържа функции от формата
f(p,V,T) =0, 2) U=U(p,V,T), 3) S=S(p,V,T).
Тези количества могат да бъдат сменени роли или от тях могат да се формират нови държавни функции, но във всеки случай същността на въпроса няма да се промени и ще останат две независими променливи. Теоретичната схема няма да надхвърли две степени на свобода, докато не възникне необходимостта да се вземат предвид нови физически ефекти и новите енергийни трансформации, свързани с тях, и се оказва невъзможно да се характеризират без разширяване на обхвата на аргументите и броя на държавни функции. Тогава броят на степените на свобода може да се промени.
(2.1)3. Свободна енергия (енергия на Хелмхолц) и нейната роля.
Препоръчително е да се опише състоянието на изотермична система с постоянен обем с помощта на свободна енергия (функция на Хелмхолц). При тези условия това е характерна функция и изохорно-изотермичен потенциал на системата.
Чрез частична диференциация от него могат допълнително да бъдат извлечени други необходими термодинамични характеристики, а именно:
(3.1)Възможно е да се конструира ясна форма на функцията на свободната енергия за някои относително прости системи, като се използва методът на статистическата термодинамика.
4. За баланса.
При всеки естествен (спонтанен или свободен) процес, свободната енергия на системата намалява. Когато системата достигне състояние на термодинамично равновесие, нейната свободна енергия достига минимум и, вече в равновесие, след това запазва постоянна стойност. Системата може да бъде изведена от равновесие поради външни сили, увеличавайки нейната свободна енергия. Такъв процес вече не може да бъде безплатен - той ще бъде принуден.
Микроскопичните движения на частиците не спират дори в равновесие и в система, състояща се от огромен брой частици и подсистеми от всякакво естество, са възможни много различни конкретни варианти и комбинации на отделни части и вътре в тях, но всички те не носят системата е извън равновесие.
Термодинамичното равновесие в една макросистема изобщо не означава, че всички видове движение изчезват в нейните микроскопични фрагменти. Напротив, балансът се осигурява от динамиката на точно тези микроскопични движения. Те извършват непрекъснато нивелиране - изглаждане на наблюдаваните макроскопични признаци и свойства, предотвратявайки тяхното излъчване и прекомерни флуктуации.
5. За статистическия метод.
Основната цел на статистическия метод е да установи количествена връзка между характеристиките механични движенияотделни частици, които съставляват равновесен статистически колектив, и осреднените свойства на този колектив, които са достъпни за термодинамични измервания чрез макроскопични методи.
Целта е да се изведат количествени закономерности за термодинамичните параметри на системата въз основа на механичните характеристики на движенията на отделни микроелементи от равновесен колектив.
6. Равновесия и флуктуации. Микродържави.
Според метода на Гибс термодинамичната система е колектив - съвкупност от много голям брой елементи - еднотипни подсистеми.
Всяка подсистема от своя страна също може да се състои от много голям брой други още по-малки подсистеми и от своя страна да играе ролята на напълно независима система.
Всички естествени флуктуации в една равновесна система не нарушават равновесието; те са съвместими със стабилното макроскопично състояние на огромен колектив от частици. Те просто преразпределят характеристиките на отделните елементи на колектива. Възникват различни микросъстояния и всички те са версии на едно и също наблюдавано макросъстояние.
Всяка отделна комбинация от състояния на елементите на колектива генерира само едно от огромното разнообразие от възможни микросъстояния на макросистемата. Всички са вътре физически смисълса еквивалентни, всички водят до един и същ набор от измерими физически параметри на системата и се различават само в някои детайли на разпределението на състоянията между елементите...
Всички микросъстояния са съвместими с макроскопичното термодинамично равновесие и численото разпространение на отделните компоненти на свободната енергия (нейната енергия и ентропия) е напълно обичайно обстоятелство. Трябва да разберем, че разсейването възниква поради непрекъснатия обмен на енергия между частиците - елементи на колектива. За някои елементи тя намалява, но за други се увеличава.
Ако системата е в термостат, тогава енергията се обменя непрекъснато с околната среда. Естественото енергийно смесване на колектива възниква поради непрекъснат обмен между микрочастиците на колектива. Равновесието се поддържа постоянно чрез термичен контакт с външен термостат. Така най-често се нарича в статистиката. заобикаляща среда.
7. Метод на Гибс. Статистически ансамбъл и неговите елементи.
При създаването на универсална схема на статистическата механика Гибс използва изненадващо проста техника.
Всяка реална макроскопична система е съвкупност от огромно разнообразие от елементи - подсистеми. Подсистемите могат да имат макроскопични размери и могат да бъдат микроскопични, до атоми и молекули. Всичко зависи от разглеждания проблем и нивото на изследване.
В различни моменти от време в различни точки на реална система, в различни пространствени региони на макроскопичен колектив, моментните характеристики на неговите малки елементи могат да бъдат различни. „Хетерогенностите“ в екипа непрекъснато мигрират.
Атомите и молекулите могат да бъдат в различни квантови състояния. Колективът е огромен и съдържа различни комбинации от състояния на физически идентични частици. На атомно-молекулно ниво винаги се обменят състояния и става тяхното непрекъснато смесване. Благодарение на това свойствата на различни фрагменти от макроскопичната система са подравнени и физически наблюдаваното макроскопично състояние на термодинамичната система изглежда непроменено външно...
Лекция 2.
Термодинамика, статистическа физика, информационна ентропия
1. Информация от термодинамиката и статистическата физика. Разпределителна функция. Теорема на Лиувил. Микроканонично разпределение. Първият закон на термодинамиката. Адиабатни процеси. Ентропия. Статистическо тегло. Формула на Болцман. Втори закон на термодинамиката. Обратими и необратими процеси.
2. Информационна ентропия на Шанън. Хапки, ядки, тритове и др. Връзка между ентропия и информация.
Тази част принадлежи към лекция 1. По-добре е да се разгледа в раздел V („Концепцията за заплитане на квантови състояния“).
LE CNOT е изобразен като:
Ние съхраняваме стойността на (qu)bit a, докато (qu)bit b се променя според закона XOR:
малко b(target = target) променя състоянието си тогава и само ако състоянието на контролния бит асъвпада 1; В същото време състоянието на контролния бит не се променя.
Логическата операция XOR (CNOT) илюстрира защо класическите данни могат да бъдат клонирани, но квантовите не могат. Обърнете внимание, че в общия случай под квантови данни ще разбираме суперпозиции на формата
, (1)
къде и - комплексни числаили амплитуди на състоянието и, .
Според таблицата на истината, ако XOR се приложи към булеви данни, в които вторият бит е в състояние "0" (b), а първият е в състояние "X" (a), тогава първият бит не се променя, а вторият става негово копие:
U XOR (X, 0) = (X, X), където X = “0” или “1”.
В квантовия случай данните, обозначени със символа „X“, трябва да се считат за суперпозиция (1):
.
Физически данните могат да бъдат кодирани, например, в поляризационната база |V> = 1, |H> = 0 (H,V)= (0,1):
И 
Вижда се, че действително се извършва копиране на състояние. Теоремата за забрана на клонирането гласи, че е невъзможно да се копира произволен квантово състояние. В разглеждания пример е възникнало копиране, тъй като операцията е извършена в собствена база (|0>, |1>), т.е. V частенслучай на квантово състояние.
Изглежда, че операцията XOR може да се използва и за копиране на суперпозиции на две булеви състояния, като |45 0 > ? |V> + |H>:
Но това не е вярно! Унитарността на квантовата еволюция изисква суперпозиция на входни състояния да бъде трансформирана в съответна суперпозиция на изходни състояния:
(2)
Това е т.нар заплетено състояние (Ф+), в което всеки от двата изходни кубита няма определена стойност (в случая поляризация). Този пример показва това логически операции, извършвани върху квантови обекти, се случват по различни правила, отколкото в класическите изчислителни процеси.
Възниква следващият въпрос: Изглежда, че е в изходен режим Аотново може да се представи като суперпозиция 
, като състоянието на модата b. Как да покажем, че това не е така, т.е. че изобщо няма смисъл да говорим за режимни (битови) състояния? аи мода (малко) b?
Нека използваме поляризационната аналогия, когато
(3).
Има два начина. Път 1 е по-дълъг, но по-последователен. Необходимо е да се изчислят средните стойности на параметрите на Stokes за двата изходни режима. Средните стойности са взети от вълновата функция (2). Ако всички освен се окажат равни на нула, тогава това състояние е неполяризирано, т.е. смесен и суперпозиция (3) няма смисъл. Работим в представянето на Хайзенберг, когато операторите се трансформират, но вълновата функция не.
И така, намираме го в модата а.
- общ интензитет на лъча a,
- пропорция на вертикална поляризация,
- споделяне на +45 0-та поляризация,
- дял на дясната кръгова поляризация.
Вълновата функция, върху която се извършва осредняването, се приема във формата (2):
къде са операторите за раждане и унищожаване в модовете аИ bработи по правилата:
(Направете изчисленията в Раздел V (вижте тетрадката). Там също изчислете вероятността за регистриране на съвпадения или корелатор на формата 
}
Път II е по-визуален, но по-малко „честен“!
Да намерим зависимостта на интензитета на светлината в режима авърху ъгъла на въртене на Polaroid, поставен в този режим. Това е стандартен квантов оптичен начин за проверка на състоянието (2) - интензитетът не трябва да зависи от въртенето. В същото време подобна зависимост на броя на съвпаденията има формата
. Такива зависимости са получени за първи път от E. Fry (1976) и A. Aspek (1985) и често се тълкуват като доказателство за нелокалност квантова механика.
И така, експерименталната ситуация е изобразена на фигурата:
А-приори
където е операторът за анихилация в режим a. Известно е, че трансформацията на операторите на два ортогонално поляризирани режима x и y, когато светлината преминава през поляроид, ориентиран под ъгъл, има формата:
.
(само първият, четвъртият, петият и осмият член са различни от нула) =
(само първият и осмият член са различни от нула) = - не зависи от ъгъла?!
Физически това се случва, защото вълновата функция (2) не е факторизирана и няма смисъл да говорим за състояния в режимите АИ bотделно. Следователно не може да се твърди, че режим a е в състояние на суперпозиция (3)!
Коментирайте. Направените изчисления (Път II) изобщо не доказват, че държавата е на мода Анеполяризирана. Например, ако в този режим имаше кръгово поляризирана светлина, резултатът би бил същият. Строго доказателство - например чрез параметрите на Стокс (в раздел V).
Обърнете внимание, че като действаме по същия начин, можем да докажем, че състоянието в режим a преди елемента CNOT е поляризирано.
Тук осредняването трябва да се извърши върху вълновата функция на първоначалното състояние (3). Резултатът изглежда така:
тези. максималният брой се постига при = 45 0 .
Информация и ентропия.
Без да въвеждаме засега „оперативния“ термин „информация“, ще спорим с „ежедневния“ език. Тези. информацията е известно знание за обект.
Следващият пример показва, че понятията информация и ентропия са тясно свързани. Помислете за идеален газ, разположен в термодинамично равновесие. Газът се състои от огромен брой молекули, които се движат в обем V. Параметрите на състоянието са налягане и температура. Броят на състоянията на такава система е огромен. Ентропията на газ при TD равновесие е максимална и, както следва от формулата на Болцман, се определя от броя на микросъстоянията на системата. В същото време не знаем нищо за това в какво конкретно състояние е системата този моментНямаме време - информацията е минимална. Да кажем, че по някакъв начин успяхме, използвайки много бързо устройство, да „надникнем в състоянието на системата в даден момент. Така че получихме информация за нея. Можете дори да си представите, че снимахме не само координатите на молекулите, но и техните скорости (например, като направихме няколко снимки една след друга). Освен това във всеки момент от времето, когато информацията за състоянието на системата е достъпна за нас, ентропията клони към нула, т.к. системата е само в едно конкретно състояние от цялото им огромно разнообразие и това състояние е силно неравновесно. Този пример показва, че информацията и ентропията наистина са някак свързани и естеството на връзката вече се очертава: колкото повече информация, толкова по-малко ентропия.
Информация от термодинамиката и статистическата физика.
Физическите величини, които характеризират макроскопичните състояния на телата (много молекули), се наричат термодинамични (включително енергия, обем). Има обаче величини, които се появяват в резултат на действието на чисто статистически закони и имат смисъл, когато се прилагат само към макроскопични системи. Такива са например ентропията и температурата.
Класическа статистика
*Теорема на Лиувил. Функцията на разпределение е постоянна по фазовите траектории на подсистемата ( ние говорим заза квазизатворени подсистеми, следователно теоремата е валидна само за не много големи периоди от време, през които подсистемата се държи като затворена).
Тук - - функция на разпределение или плътност на вероятността. Въвежда се чрез вероятност w открива подсистема в елемент на фазовото пространство в този момент от време: dw = ( стр 1 ,..., пс , р 1 ,..., qs ) dpdq , и
Намирането на статистическото разпределение за всяка подсистема е основната задача на статистиката. Ако статистическото разпределение е известно, тогава е възможно да се изчислят вероятностите за различни стойности на всяка физични величини, в зависимост от състоянията на тази подсистема (т.е. от стойностите на координатите и моментите):
.
*Микроканонично разпределение.
Разпределението за множеството от две подсистеми (те се приемат за затворени, т.е. слабо взаимодействащи) е равно. Ето защо 
- логаритъм на функцията на разпределение - стойност добавка. От теоремата на Лиувил следва, че функцията на разпределение трябва да бъде изразена чрез такива комбинации от променливи p и q, които, когато подсистемата се движи като затворена система, трябва да останат постоянни (такива количества се наричат интеграли на движението). Това означава, че самата функция на разпределение е неразделна част от движението. Освен това неговият логаритъм също е интеграл от движението и добавка. Общо в механиката има седем интеграла на движението - енергия, три компонента на импулса и три компонента на ъгловия момент - (за подсистема a: E a (стр,
р),
П
А (стр,
р), МА (стр,
р)). Единствената допълнителна комбинация от тези количества е
Освен това коефициентите (има седем от тях) трябва да останат еднакви за всички подсистеми на дадена затворена системаи се избира от условията за нормализиране (4).
За да бъде изпълнено условието за нормализиране (4), е необходимо функцията (стр, р) се свърза с точките E 0, P 0, M 0 до безкрайност. По-точна формулировка дава израза
Микроканонично разпределение.
Наличието на - функции гарантира, че те изчезват за всички точки от фазовото пространство, в които поне една от величините Д, Р, М не е равно на дадената му (средна) стойност E 0, P 0, M 0 .
От шест интеграла П И М могат да бъдат елиминирани чрез затваряне на системата в солидна кутия, в която лежи.
.
Физическа ентропия
Отново използваме концепцията за идеален газ.
Нека моноатомен идеален газ с плътност ни температура Tзаема обем V. Ще измерваме температурата в енергийни единици - константата на Болцман няма да се появи. Всеки газов атом има средна кинетична енергия топлинно движение, равна на 3T/2. Следователно общата топлинна енергия на газа е равна на
Известно е, че налягането на газа е равно на стр = nT. Ако газът може да обменя топлина с външната среда, тогава законът за запазване на енергията на газа изглежда така:
. (5)
По този начин промяна във вътрешната енергия на газ може да възникне както поради работата, която извършва, така и поради получаването на определено количество топлина dQотвън. Това уравнение изразява първия закон на термодинамиката, т.е. закон за запазване на енергията. Приема се, че газът е в равновесие, т.е. стр = конств целия обем.
Ако приемем, че газът също е в състояние на TD равновесие, Т =конст, то съотношението (5) може да се разглежда като елементарен процес на изменение на параметрите на газа, когато те се променят много бавно, когато равновесието на TD не е нарушено. Именно за такива процеси понятието ентропия S се въвежда с помощта на връзката
По този начин се твърди, че в допълнение към вътрешната енергия, равновесният газ има друга вътрешна характеристика, свързана с топлинното движение на атомите. Съгласно (5, 6) при постоянен обем dV= 0, изменението на енергията е пропорционално на изменението на температурата, а в общия случай
защото 
Където н =
nV =
консте общият брой газови атоми, тогава последното отношение може да се запише като
След интегрирането получаваме
Изразът в квадратни скоби представлява ентропията на частица.
Така, ако температурата и обемът се променят по такъв начин, че VT 3/2 остава постоянна, тогава ентропията S не се променя. Съгласно (6) това означава, че газът не обменя топлина с външната среда, т.е. газът е отделен от него чрез топлоизолационни стени. Този процес се нарича адиабатен.
Тъй като
където = 5/3 се нарича адиабатен показател. Така по време на адиабатен процес температурата и налягането се променят с плътността според закона
Формула на Болцман
Както следва от теоремата на Лиувил, функцията на разпределение? има остър максимум при E = E 0 (средна стойност) и е различен от нула само в близост до тази точка. Ако въведете ширината E на кривата (E), дефинирайки я като ширината на правоъгълник, чиято височина е равна на стойността на функцията (E) в максималната точка, а площта е равна на единица 
(с правилна нормализация). Можем да преминем от интервала на енергийните стойности до броя на състоянията Г с енергии, принадлежащи на E (това всъщност е средното колебание на енергията на системата). Тогава стойността Γ характеризира степента на размазване на макроскопичното състояние на системата върху нейните микроскопични състояния. С други думи, за класическите системи Г е размерът на областта на фазовото пространство, в която дадена подсистема прекарва почти цялото си време.В квазикласическата теория се установява съответствие между обема на областта на фазовото пространство и броят на квантовите състояния на него, а именно, за всяко квантово състояние във фазовото пространство има клетка с обем , където s е броят на степените на свобода
Стойността Γ се нарича статистическо тегло на макроскопичното състояние; може да се запише като:
Логаритъмът на статистическото тегло се нарича ентропия:
където - статистическо тегло = брой микросъстояния, обхванати от макросъстоянието на разглежданата система.
.
В квантовата статистика е показано, че = 1. Тогава
Където под се има предвид статистическа матрица (плътност). Поради линейността на логаритъма на функцията на разпределение на енергията (*), където осредняването се извършва върху функцията на разпределение.
Тъй като броят на състоянията във всеки случай не е по-малък от едно, ентропията не може да бъде отрицателна. S определя плътността на нивата в енергийния спектър на макроскопична система. Поради адитивността на ентропията можем да кажем, че средните разстояния между нивата на макроскопично тяло намаляват експоненциално с увеличаване на неговия размер (т.е. броя на частиците в него). Най-висока стойностентропията съответства на пълното статистическо равновесие.
Характеризирайки всяко макроскопично състояние на системата чрез разпределението на енергията между различни подсистеми, можем да кажем, че редица последователно преминати състояния от системата съответстват на все по-вероятно разпределение на енергията. Това увеличение на вероятността е голямо поради експоненциалния си характер e S- показателят съдържа добавъчна величина - ентропия. Че. процесите, протичащи в неравновесна затворена система, протичат по такъв начин, че системата непрекъснато преминава от състояния с по-ниска ентропия към състояния с по-висока ентропия. В резултат на това ентропията достига възможно най-високата стойност, съответстваща на пълно статистическо равновесие.
По този начин, ако една затворена система в даден момент от времето е в неравновесно макроскопично състояние, тогава най-вероятната последица в следващите моменти ще бъде монотонно увеличение на ентропията на системата. Това - втори закон на термодинамиката (Р. Клаузиус, 1865 г.). Статистическата му обосновка е дадена от Л. Болцман през 1870 г. Друго определение:
ако в някакъв момент ентропията на затворена система е различна от максималната, то в следващите моменти ентропията не намалява. Тя се увеличава или в краен случай остава постоянна. Според тези две възможности всички процеси, протичащи с макроскопични тела, обикновено се разделят на необратим И обратими . Необратимо - тези процеси, които са придружени от увеличаване на ентропията на цялата затворена система (процеси, които биха били техните повторения в обратен ред, не може да възникне, тъй като в този случай ентропията ще трябва да намалее). Имайте предвид, че намаляването на ентропията може да бъде причинено от колебания. Реверсивна са процеси, при които ентропията на затворена система остава постоянна и които следователно могат да протичат в обратна посока. Строго обратим процес представлява идеален ограничаващ случай.
По време на адиабатни процеси системата не абсорбира и не отделя топлина ? Q = 0 .
коментар: (съществено). Твърдението, че една затворена система трябва за достатъчно дълго време (по-дълго от времето на релаксация) да премине в състояние на равновесие, се отнася само за система в стационарно външни условия. Пример за това е поведението на голяма област от Вселената, достъпна за нашето наблюдение (свойствата на природата нямат нищо общо със свойствата на равновесна система).
Информация.
Нека разгледаме лента, разделена на клетки - класически регистър. Ако само един от два знака може да бъде поставен във всяка клетка, тогава се казва, че клетката съдържа малко информация. Очевидно е (вижте лекция 1), че в регистъра, съдържащ нсъдържащи се клетки нмалко информация и може да се запише в него 2 нсъобщения. И така, информационната ентропия се измерва в битове:
(7)
Тук Q N = 2 н- общият брой различни съобщения. От (7) е ясно, че информационната ентропия е просто равна на минималния брой двоични клетки, с които може да се запише някаква информация.
Определение (7) може да бъде пренаписано по различен начин. Нека имаме много Q Nразлични съобщения. Нека намерим вероятността съобщението, от което се нуждаем, да съвпадне с произволно избрано от общия брой Q Nразлични съобщения. Очевидно е равно на P N = 1/ Q N. Тогава дефиниция (7) ще бъде записана като:
(8)
Колкото по-голям е броят на клетките н, толкова по-малка е вероятността P Nи толкова по-голяма е информационната ентропия H Bсъдържащи се в това конкретно съобщение.
Пример . Броят на буквите от азбуката е 32 (без буквата ё). Числото 32 е петата степен на две 32 = 2 5. За да свържете всяка буква с конкретна комбинация от двоични числа, трябва да имате 5 клетки. Добавяйки главни букви към малки букви, ние удвояваме броя на знаците, които искаме да кодираме - ще бъдат 64 = 2 6 - т.е. добавя се допълнителна информация H B= 6. Тук H B- количеството информация на буква (малка или главна). Такова директно изчисляване на информационната ентропия обаче не е съвсем точно, тъй като има букви в азбуката, които са по-рядко срещани или по-често срещани. Тези букви, които са по-рядко срещани, могат да бъдат дадени голямо количествоклетки, а на често срещани букви - запазете и им придайте тези регистрационни състояния, които заемат по-малък брой клетки. Точно определениеинформационната ентропия е дадена от Шанън:
(9)
Формално извеждането на тази връзка може да бъде обосновано по следния начин.
Показахме по-горе това
поради адитивността на логаритъма на функцията на разпределение и нейната линейност по енергия.
Позволявам стр- разпределителна функция от някакъв вид дискретна стойност f i (например буквите „o“ в този текст). Ако използвате функцията стрконструирайте функцията на разпределение на вероятностите на различни стойности на количеството f = f 1 , f 2 ,... е Н, тогава тази функция ще има максимум при , където и (нормализиране). Тогава p()= 1 и (най-общо казано, това е вярно за класа функции, удовлетворяващи условието (*))
Сумирането се извършва върху всички знаци (букви от азбуката) и p iозначава вероятността за появата на символ с число аз. Както можете да видите, този израз обхваща както често използвани букви, така и букви, чиято вероятност да се появят в дадено съобщение е малка.
Тъй като израз (9) използва натурален логаритъм, съответната единица информация се нарича „nat“.
Израз (9) може да бъде пренаписан като
където скобите означават обичайното класическо осредняване с помощта на функцията на разпределение p i .
Коментирайте . В следващите лекции ще бъде показано, че за квантовите състояния
където е матрицата на плътността. Формално изразите (10) и (11) са еднакви, но има съществена разлика. Класическото осредняване се извършва върху ортогонални (собствени) състояния на системата, докато за квантовия случай може да има и неортогонални състояния (суперпозиции). Затова винаги H количество H клас !
Формули (8) и (9) използват логаритми в различни бази. В (8) - на базата на база 2, а в (9) - на базата на д. Съответстващи на тези формули информационни ентропиимогат лесно да се изразят един чрез друг. Нека използваме връзката, в която М е произволно число
.
Тогава, като се има предвид това 
и получаваме
- броят на битовете е почти един и половина пъти по-голям от броя на nat!
Разсъждавайки по подобен начин, можем да получим връзката между ентропиите, изразени в тритове и битове:
В компютърните технологии информацията се използва в двоична база (в битове). За разсъждения във физиката е по-удобно да се използва информация на Шанън (в Nat), която може да характеризира всяка дискретна информация. Винаги можете да намерите броя на съответните битове.
ВРЪЗКАТА НА ЕНТРОПИЯ И ИНФОРМАЦИЯ. Демонът на Максуел
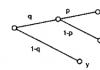
Този парадокс е разгледан за първи път от Максуел през 1871 г. (виж фиг. 1). Нека някаква „свръхестествена“ сила отваря и затваря клапана в съд, разделен на две части и съдържащ газ. Вентилът се контролира от правилото, че се отваря, ако бързи молекули, движещи се отдясно наляво, го докоснат или ако бавни молекули го ударят, движейки се в обратна посока. Така демонът въвежда температурна разлика между два обема, без да извършва работа, което нарушава втория закон на термодинамиката.
Демонът на Максуел. Демонът установява разлика в налягането, като отваря амортисьора, когато броят на газовите молекули, които го удрят отляво, надвишава броя на ударите отдясно. Това може да стане по напълно обратим начин, стига паметта на демона да съхранява произволните резултати от неговите наблюдения на молекули. Следователно паметта на демона (или главата му) се нагрява. Необратимата стъпка не е, че информацията се натрупва, а тази информация се губи, когато демонът по-късно изчисти паметта. По-горе: Запълването на паметта на демона с битове информация е случаен процес. От дясната страна на пунктираната линия е празна област на паметта (всички клетки са в състояние 0, отляво са произволни битове). Отдолу има демон.
Направени са редица опити за разрешаване на парадокса или прогонване на демона. Например, предполагаше се, че демонът не може да извлича информация, без да върши работа или без да смущава (т.е. да нагрява) газа - но се оказа, че това не е така! Други опити се свеждат до факта, че вторият принцип може да бъде нарушен под въздействието на определени „разумни“ или „мислещи“ сили (създания). През 1929г Лео Силард значително „напредна“ решението на проблема, свеждайки го до минимална формулировка и подчертавайки основните компоненти. Основното нещо, което Демонът трябва да направи, е да установи дали една молекула е разположена отдясно или отляво на плъзгащия се клапан, което би позволило извличането на топлина. Това устройство беше наречено двигател Szilard. Силард обаче не разреши парадокса, защото неговият анализ не взе предвид как измерването, чрез което демонът знае дали дадена молекула е отдясно или отляво, влияе върху увеличаването на ентропията (вижте фигурата Szilard_demon.pdf). Двигателят работи на шестстепенен цикъл. Двигателят е цилиндър с бутала в краищата. В средата се вкарва капак. Работата по натискането на дяла може да бъде намалена до нула (Szilard показа това). Има и устройство за памет (MU). Може да бъде в едно от трите състояния. „Празно“, „Молекула отдясно“ и „Молекула отляво“. Първоначално състояние: НАГОРЕ = „Празно“, буталата са изтласкани навън, преградата е разширена, молекулата има Средната скорост, което се определя от температурата на термостата (слайд 1).
1. Преградата се поставя, оставяйки молекулата отдясно или отляво (слайд 2).
2. Устройството с памет определя къде е молекулата и се премества в „дясно“ или „ляво“ състояние.
3. Компресия. В зависимост от състоянието на UE, буталото се движи от страната, където няма молекула. Този етап не изисква никаква работа. Тъй като вакуумът е компресиран (слайд 3).
4. Преградата се отстранява. Молекулата започва да упражнява натиск върху буталото (слайд 4).
5. Работен ход. Молекулата удря буталото, което го кара да се движи в обратна посока. Енергията на молекулата се предава на буталото. Докато буталото се движи, средната му скорост трябва да намалява. Това обаче не се случва, тъй като стените на съда са с постоянна температура. Следователно топлината от термостата се прехвърля към молекулата, поддържайки нейната скорост постоянна. Така по време на работния ход топлинната енергия, подадена от термостата, се преобразува в механична работа, извършена от буталото (слайд 6).
6. Почистване на UE, връщане в състояние „Празно“ (слайд 7). Цикълът е завършен (слайд 8 = слайд 1).
Изненадващо е, че този парадокс не е разрешен до 80-те години. През това време беше установено, че по принцип всеки процес може да се извърши по обратим начин, т.е. без „заплащане“ чрез ентропия. И накрая, Бенет през 1982г установи окончателната връзка между това твърдение и парадокса на Максуел. Той предположи, че демонът може действително да знае къде се намира дадена молекула в двигателя на Szilard, без да върши работа или да увеличава ентропията на околната среда (термостата) и по този начин да върши полезна работа в един цикъл на двигателя. Информацията за позицията на молекулата обаче трябва да остане в паметта на демона (rsi.1). Като завършен Повече ▼цикли, все повече информация се натрупва в паметта. За да завърши термодинамичния цикъл, демонът трябва да изтрие информацията, съхранена в паметта. Именно тази операция на изтриване на информация трябва да се класифицира като процес на увеличаване на ентропията на околната среда, както се изисква от втория принцип. Това завършва основната физическа част от демоничното устройство на Максуел.
Тези идеи получиха известно развитие в произведенията на Д. Д. Кадомцев.
Нека разгледаме идеален газ, състоящ се само от една частица (Кадомцев, „динамика и информация“). Това не е абсурдно. Ако една частица е затворена в съд с обем V със стени при температура Т, то рано или късно тя ще влезе в равновесие с тези стени. Във всеки момент от времето тя е завършена определена точкапространство и с много специфична скорост. Ние ще извършваме всички процеси толкова бавно, че частицата ще има време средно да запълни целия обем и многократно да променя величината и посоката на скоростта по време на нееластични сблъсъци със стените на съда. Така частицата упражнява средно налягане върху стените и има температура Tи неговото разпределение на скоростта е максвелово с температурата T. Тази система от една частица може да се компресира адиабатично, нейната температура може да се променя, което й дава възможност да влезе в равновесие със стените на съда.
Средно налягане върху стената при н = 1 , равно на стр= T/V, А средна плътност n= 1/ V. Нека разгледаме случая на изотермичен процес, когато Т =конст. От първото начало при Т =конст. И стр= T/Vполучаваме
, тъй като
От тук откриваме, че промяната в ентропията не зависи от температурата, така че
Тук се въвежда интеграционната константа: „размер на частиците“< Работа в изотермичен процес работата се определя от разликата в ентропията. Да предположим, че имаме идеални прегради, които могат да се използват за разделяне на съда на части без загуба на енергия. Нека разделим нашия съд на две равни части с обем V/2
всеки. В този случай частицата ще бъде в една от половините - но не знаем коя. Да кажем, че имаме устройство, което ни позволява да определим в коя част се намира дадена частица, например прецизна скала. След това от симетрично разпределение на вероятностите от 50% до 50%, което е в две половини, получаваме 100% вероятност за една от половините - възниква „срив“ на разпределението на вероятностите. Съответно, новата ентропия ще бъде по-малка от първоначалната ентропия със сумата Чрез намаляване на ентропията може да се извърши работа. За да направите това, достатъчно е да преместите дяла към празния обем, докато изчезне. Работата ще бъде равна на Ако нищо не се е променило във външния свят, тогава чрез повтаряне на тези цикли е възможно да се изгради вечен двигател от втори вид. Това е демонът на Максуел във версията на Силард. Но вторият закон на термодинамиката забранява получаването на работа само чрез топлина. Това означава, че нещо трябва да се случва във външния свят. Какво е това? Откриване на частица в една от половините променя информацията за частица -
От двете възможни половини е посочена само една, в която се намира частицата. Това знание отговаря на един бит информация. Процесът на измерване намалява ентропията на частицата (превод в равновесно състояние) и увеличава информацията за системата (частицата) точно по същия начин. Ако многократно разделяте наполовина предварително получените половини, четвърти, осмини и т.н., тогава ентропията последователно ще намалява и информацията ще се увеличава! С други думи Колкото повече знаем за една физическа система, толкова по-ниска е нейната ентропия. Ако всичко е известно за системата, това означава, че сме я прехвърлили в силно неравновесно състояние, когато нейните параметри са възможно най-далеч от равновесните стойности. Ако в нашия модел частицата може да бъде поставена в елементарна клетка от обем V 0
, след това по същото време С = 0
, а информацията достига своята максимална стойност И така, информационна ентропияе мярка за липсата (или степента на несигурност) на информация за действителното състояние на физическа система. Информационна ентропия на Шанън: Количество информация
аз(или просто информация) за състоянието на класическа система, получена в резултат на измервания от външно устройство, свързано към разглежданата система чрез някакъв комуникационен канал, се определя като разликата в информационната ентропия, съответстваща на първоначалната несигурност на системата състояние з 0
, и информационна ентропия на крайното състояние на системата след измерване з. По този начин, аз
+
з
=
з
0
=
конст
.
В идеалния случай, когато в комуникационния канал няма шум и смущения, създадени от външни източници, окончателното разпределение на вероятността след измерване се свежда до една конкретна стойност p n= 1, т.е. з =
0, а максимална стойностИнформацията, получена по време на измерването, ще се определя от:
Imax =
з 0
. По този начин информационната ентропия на Шанън на система има значението на максималната информация, съдържаща се в системата; може да се определи при идеални условия за измерване на състоянието на системата при липса на шум и смущения, когато ентропията на крайното състояние е нула: Нека разгледаме класически логически елемент, който може да бъде в едно от двете еднакво вероятни логически състояния „0” и „1”. Такъв елемент, заедно с околната среда - термостата и сигнала, генериран от външен топлоизолиран обект, образува единна неравновесна затворена система. Преходът на елемент към едно от състоянията, например към състояние „0“, съответства на намаляване на стат. теглото на състоянието му спрямо първоначалното състояние е 2 пъти (за тристепенни системи - 3 пъти). Нека намерим намалението информационна ентропияШанън, което съответства на увеличаване на количеството информация за елемент с единица, което се нарича малко: Следователно информационната ентропия определя броя на битовете, които са необходими за кодиране на информация във въпросната система или съобщение. ЛИТЕРАТУРА 1. Д. Ландау, И. Лифшиц. Статистическа физика. Част 1. Наука, М 1976. 2. М. А. Леонтович. Въведение в термодинамиката. Статистическа физика. Москва, Наука, 1983. - 416 с. 3. Б. Б. Кадомцев. Динамика и информация. UFN, 164, № 5, 449 (1994). СТАТИСТИЧЕСКА ТЕРМОДИНАМИКА, статистически раздел физика, посветена на обосноваването на законите на термодинамиката въз основа на законите на взаимодействието. и движенията на частиците, които изграждат системата. За системи в равновесно състояние C. t. позволява да се изчисли ,
записвам уравнения на състоянието,фаза и химични условия равновесия. Теорията на неравновесните системи дава обосновка за връзките термодинамика на необратими процеси(уравнения за пренос на енергия, импулс, маса и техните гранични условия) и ви позволява да изчислите кинетиката, включена в уравненията за пренос. коефициенти. С. т. задава количества. връзка между микро- и макросвойствата на физ. и хим. системи Изчислителните методи на изчислителната техника се използват във всички области на съвременната техника. теоретичен химия. Основни понятия.За статистически макроскопични описания системи Дж. Гибс (1901) предлага да се използват понятията за статист. ансамбъл и фазово пространство, което прави възможно прилагането на методите на теорията на вероятностите за решаване на проблеми. Статистически ансамбъл - съвкупност от много голям брой еднакви множествени системи. частици (т.е. „копия“ на разглежданата система), разположени в едно и също макросъстояние, което се определя параметри на състоянието;Микросъстоянията на системата могат да се различават. Основен статистически ансамбли - микроканонични, канонични, големи канонични. и изобарно-изотермични. Микроканоничен Ансамбълът на Гибс се използва, когато се разглеждат изолирани системи (без обмен на енергия E с околната среда), имащи постоянен обем V и броя на еднаквите частици N (E, VИ Н-параметри на състоянието на системата). Канонич. Ансамбълът на Гибс се използва за описание на системи с постоянен обем, които са в топлинно равновесие с околната среда (абсолютна температура T) с постоянен брой частици N (параметри на състоянието V, T, N).Голям канон. Ансамбълът на Гибс се използва за описание на отворени системи, които са в топлинно равновесие с околната среда (температура T) и материално равновесие с резервоар от частици (частиците от всички видове се обменят през „стените“, обграждащи системата с обем V). параметрите на такава система са V. , Ti mCh химичен потенциалчастици. Изобарно-изотермичен Ансамбълът на Гибс се използва за описание на системи в топлинна и козина. равновесие с околната среда при постоянно налягане P (параметри на състоянието Т, П, Н).
Фазово пространство в статистиката механиката е многомерно пространство, чиито оси са обобщени координати ази импулсите, свързани с тях
(i =1,2,..., M) системи със степени на свобода. За система, състояща се от Natoms, азИ
съответстват на декартовата координата и компонента на импулса (a = x, y, z)
определен атом j M = 3N.Наборът от координати и моменти се означават съответно с q и p. Състоянието на системата се представя от точка във фазово пространство с размерност 2M, а изменението на състоянието на системата във времето се представя от движението на точка по права, т.нар. фазова траектория. За статистически описания на състоянието на системата, понятията фазов обем (обемен елемент на фазовото пространство) и функцията на разпределение f( p, q), ръбът характеризира плътността на вероятността за намиране на точка, представяща състоянието на системата в елемент от фазовото пространство близо до точката с координати p, q. IN квантова механикаВместо фазов обем се използва концепцията за дискретна енергия. спектър на система с краен обем, тъй като състоянието на отделна частица се определя не от импулс и координати, а от вълнова функция, разрез в стационарна динамика. състоянието на системата съответства на енергията. спектър от квантови състояния. Разпределителна функциякласически система f(p, q) характеризира плътността на вероятността за реализация на дадено микросъстояние ( p, q)
в обемния елемент dG
фазово пространство. Вероятността N частици да бъдат в безкрайно малък обем на фазовото пространство е равна на: където dГ N ->елемент от фазовия обем на системата в единици h 3N , з-константа на Планк; разделител Н!отчита факта, че пренареждането на идентичностите. частици не променя състоянието на системата. Функцията на разпределение удовлетворява условието за нормализиране tf( p, q)dГ N => 1, тъй като системата е надеждно разположена в с.л. състояние. За квантовите системи функцията на разпределение определя вероятността w аз , намиране на система от N частици в квантово състояние, определено от набор от квантови числа i, с енергия подлежи на нормализация Средната стойност в момент t (т.е. за безкрайно малък интервал от време от t до t + дт) всяко физическо стойности A( p, q),
която е функция на координатите и импулсите на всички частици в системата, с помощта на функцията на разпределение се изчислява по правилото (включително за неравновесни процеси): Интегрирането по координати се извършва по целия обем на системата, а интегрирането по импулси от H, до +,. Термодинамично състояние равновесието на системата трябва да се разглежда като граница m:,. За равновесни състояния функциите на разпределение се определят без решаване на уравнението на движението на частиците, които изграждат системата. Формата на тези функции (еднаква за класическите и квантовите системи) е установена от Дж. Гибс (1901). В микроканон. в ансамбъла на Гибс всички микросъстояния с дадена енергия са еднакво вероятни и функцията на разпределение за класическата. системи има формата: е( p,q)= Ад, където d-делта функция на Дирак, H( p,q)-функция на Хамилтън, която е сумата от кинетичните. и потенциал енергии на всички частици; константата A се определя от условието за нормализиране на функцията f( p, qЗа квантовите системи, с точност на определяне на квантовото състояние, равна на стойността DE, в съответствие с връзката на несигурност между енергия и време (между импулса и координатата на частицата), функцията w( )
= -1, ако E E+д Д,и w( )
= 0 ако
И
д д.Стойност g( E, N, V)-T. Наречен статистически тегло, равно на броя на квантовите състояния в енергията. слой DE. Важна връзка между ентропията на системата и нейните статистически данни. тегло: С( E, N, V)= k lng( E, N, V),Където k-константа на Болцман. В канон. Вероятност на ансамбъла на Гибс за намиране на система в микросъстояние, определено от координатите и импулсите на всички N частици или стойности , има формата: f( p, q) =
exp(/ kT); w аз,Н= exp[(F - E аз,Н)/kT], където F-свободен. енергия (енергия на Хелмхолц), в зависимост от стойностите V, T, N: F = -kTвътре
Където
статистически сума (в случай на квантова система) или статистическа. интеграл (в случай на класическа система), определен от условието за нормализиране на функции w i,N >или f( p, q): Z N = Тexp[-H(р, q)/ kT]dpdq/() (сумата по r се взема за всички квантови състояния на системата и интегрирането се извършва върху цялото фазово пространство). Във великия канон. Функция на разпределение на ансамбъла на Гибс f( p, q)
и статистически сумата X, определена от условието за нормализиране, има формата: където W-термодинамичен. променлив зависим потенциал V, T, m (сумирането се извършва върху всички положителни числа N).В изобарно-изотермично. Разпределение на ансамбъла на Гибс и статистическа функция. сума Q,определени от условието за нормализиране, имат формата: Където G-Енергия на Гибс на системата (изобарно-изотермичен потенциал, свободна енталпия). За изчисляване на термодинамика функции, можете да използвате всяко разпределение: те са еквивалентни една на друга и съответстват на различни физически. условия. Микроканоничен Прилага се разпределението на Гибс. обр. в теоретичната изследвания. За решаване на конкретни проблеми се разглеждат ансамбли, в които има обмен на енергия с околната среда (каноничен и изобарно-изотермичен) или обмен на енергия и частици (голям каноничен ансамбъл). Последният е особено удобен за изучаване на фаза и химия. равновесия. Статистически суми
и Q ни позволяват да определим енергията на Хелмхолц F, енергията на Гибс G,както и термодинамични. свойства на системата, получени чрез диференциране на статист. количества според съответните параметри (на 1 мол вещество): вътр. енергия U = RT 2 (9лн
)V , >енталпия H = RT 2 (9лн ,
ентропия S = Rln + RT(9лн /9T) V= = Rln Q+RT(9лн , топлинен капацитет при постоянен обем C V= 2RT(9лн
2 (вътре /9T 2)V , >топлинен капацитет при постоянно налягане S P => 2RT(9лн
2 (9 2 ин /9T 2) P>пр. Респ. всички тези количества придобиват статистическа значимост. значение. Така, вътрешна енергиясе идентифицира със средната енергия на системата, което ни позволява да разгледаме първи закон на термодинамикатакато закон за запазване на енергията по време на движението на частиците, съставляващи система; Безплатно енергията е свързана със статистиката сумата на системата, ентропия - с броя на микросъстоянията g в дадено макросъстояние, или статист. теглото на макросъстоянието и следователно с неговата вероятност. Значението на ентропията като мярка за вероятността от състояние се запазва по отношение на произволни (неравновесни) състояния. В състояние на равновесие, изолиран. система има максималната възможна стойност за даден външен. условия ( E, V, N), т.е. равновесното състояние е най-много. вероятно състояние (с максимална статистическа тежест). Следователно преходът от неравновесно състояние към равновесно състояние е процес на преход от по-малко вероятни състояния към по-вероятни. Това е статистическата точка. значението на закона за нарастваща ентропия, според който ентропията на затворена система може само да нараства (вж. Втори закон на термодинамиката).При т-ре абс. нула, всяка система е фундаментално състояние, в което w 0 = 1 и S= 0. Това твърдение представлява (вж Топлинна теорема). Важно е, че за еднозначно определяне на ентропията е необходимо да се използва квантово описание, тъй като в класическата статистика ентропия m.b. се определя само до произволен член. Идеални системи. Изчисляване на статистически суми на повечето системи е трудна задача. Това е значително опростено в случай на газове, ако приносът на потенциала. енергия в общата енергия на системата може да се пренебрегне. В този случай пълната функция на разпределение f( p, q)
за N частици на идеална система се изразява чрез произведението на функциите на разпределение на една частица f 1 (p, q): Разпределението на частиците между микросъстоянията зависи от тяхната кинетика. енергия и от квантовите свойства на системата, определени от идентичността на частиците. В квантовата механика всички частици се разделят на два класа: фермиони и бозони. Типът статистика, на която се подчиняват частиците, е уникално свързан с тяхното въртене. Статистиката на Ферми-Дирак описва разпределението в система от идентичности. частици с полуцяло число спин 1 / 2, 3 / 2,... в единици P = h/2p. Извиква се частица (или квазичастица), която се подчинява на определените статистики. фермион. Фермионите включват електрони в атоми, метали и полупроводници, атомни ядра с нечетен атомен номер, атоми с нечетна разлика между атомния номер и броя на електроните, квазичастици (например електрони и дупки в твърди тела) и т.н. Тези статистики бяха предложен от Е. Ферми през 1926 г.; през същата година П. Дирак открива нейната квантова механика. значение. Вълновата функция на фермионна система е антисиметрична, т.е. тя променя знака си, когато координатите и спиновете на всяка двойка идентичности се пренаредят. частици. Във всяко квантово състояние не може да има повече от една частица (вж. Принципът на Паули).
Среден брой частици идеален газ от фермиони в състояние с енергия ,
се определя от функцията на разпределение на Ферми-Дирак: =(1+exp[( -м)/ kT]} -1 , където i е набор от квантови числа, характеризиращи състоянието на частицата. Статистиката на Бозе-Айнщайн описва системи от идентичности. частици с нулев или цял спин (0, R, 2P,
...). Извиква се частица или квазичастица, която се подчинява на определените статистики. бозон. Тази статистика е предложена от S. Bose (1924) за фотони и развита от A. Einstein (1924) във връзка с идеални газови молекули, разглеждани като съставни частици от четен брой фермиони, например. атомни ядра с четен общ брой протони и неутрони (дейтрон, 4 He ядро и др.). Бозоните включват също фонони в твърди тела и течен 4He, екситони в полупроводници и диелектрици. Вълновата функция на системата е симетрична по отношение на пермутацията на всяка двойка идентичности. частици. Числата на заемане на квантовите състояния не са ограничени от нищо, т.е. произволен брой частици могат да бъдат в едно състояние. Среден брой частици идеален газ от бозони в състояние с енергия E iсе описва от функцията на разпределение на Бозе-Айнщайн: =(exp[( -м)/ kT]-1} -1 . Статистиката на Болцман е специален случай на квантовата статистика, когато квантовите ефекти могат да бъдат пренебрегнати ( висока т-ра). Той разглежда разпределението на частиците идеален газ по импулс и координати във фазовото пространство на една частица, а не във фазовото пространство на всички частици, както при разпределенията на Гибс. Като минимум единици обем на фазовото пространство, което има шест измерения (три координати и три проекции на импулса на частиците), в съответствие с квантовата механика. Поради съотношението на несигурност е невъзможно да се избере обем, по-малък от h 3 . Среден брой частици идеален газ в състояние с енергия
се описва от функцията на разпределение на Болцман: =exp[(m )/kT]. За частици, които се движат според класическите закони. механика във външния потенциал поле U(r),
статистически равновесна функция на разпределение f 1 (p,r)
според моментите pi и координатите r на частиците идеален газ има формата: f 1 (p,r) = Aexp( - [p 2 /2m + U(r)]/ kT}.
Тук p 2 /2t-кинетичен. енергията на молекулите с маса w, константа A, се определя от условието за нормализиране. Този израз често се нарича Разпределение на Максуел-Болцман, а разпределението на Болцман се нарича. функция n(r) = n 0
exp[-U(r)]/ kT], където n(r) = t f 1 (p, r) dp- плътност на броя на частиците в точка r (n 0 - плътност на броя на частиците при липса на външно поле). Разпределението на Болцман описва разпределението на молекулите в гравитационното поле (барометрично поле), молекулите и силно диспергираните частици в полето центробежни сили, електрони в неизродени полупроводници и се използва също за изчисляване на разпределението на йони в разреден. разтвори на електролити (в обема и на границата с електрода) и др. При U(r)
= 0 от разпределението на Максуел-Болцман следва разпределението на Максуел, което описва разпределението на скоростите на частиците, които са в статистическо състояние. равновесие (J. Maxwell, 1859). Според това разпределение вероятният брой молекули на единица обем, чиито компоненти на скоростта лежат в интервалите от преди + (i= x, y, z), определена от функцията: Разпределението на Максуел не зависи от взаимодействието. между частиците и е вярно не само за газове, но и за течности (ако е възможно класическо описание за тях), както и за Браунови частици, суспендирани в течност и газ. Използва се за отчитане на броя на сблъсъци на газови молекули една с друга по време на химични реакции. р-ция и с повърхностни атоми. Сума върху състоянията на молекулата.Статистически сума на идеален газ в каноничен Ансамбълът на Гибс се изразява чрез сумата на състоянията на една молекула Q 1: Където E i ->енергия на i-тото квантово ниво на молекулата (i = O съответства на нулевото ниво на молекулата), аз-статистически тегло на i-то ниво. В общия случай отделните видове движение на електрони, атоми и групи от атоми в една молекула, както и движението на молекулата като цяло са взаимосвързани, но приблизително могат да се разглеждат като независими. Тогава сумата върху състоянията на молекулата може да бъде представени под формата на продукт от отделни компоненти, свързани със стъпките. движение (Q пост) и с интрамол. движения (Q int): Q 1 = Q пост
Химическа енциклопедия. - М.: Съветска енциклопедия.
Изд. И. Л. Кнунянц.
1988
.
- (равновесна статистическа термодинамика) раздел от статистическата физика, посветен на обосноваването на законите на термодинамиката на равновесните процеси (въз основа на статистическата механика на Дж. У. Гибс) и изчисленията на термодинамиката. характеристики на физическото... Физическа енциклопедия
Клон от статистическата физика, посветен на теоретичното определяне на термодинамичните свойства на веществата (уравнения на състоянието, термодинамични потенциалии др.) въз основа на данни за структурата на веществата... Голям енциклопедичен речник
Клон на статистическата физика, посветен на теоретичното определяне на термодинамичните характеристики на физическите системи (уравнения на състоянието, термодинамични потенциали и т.н.), базирани на законите за движение и взаимодействие на частиците, които съставляват тези ... енциклопедичен речник статистическа термодинамика- statistinė termodinamika statusas T sritis chemija apibrėžtis Termodinamika, daugiadalelėms sistemus naudojanti statistinės mechanikos principus. атитикменис: англ. статистическа термодинамика рус. статистическа термодинамика... Chemijos terminų aiškinamasis žodynas статистическа термодинамика- statistinė termodinamika statusas T sritis fizika atitikmenys: англ. статистическа термодинамика вок. statistische Thermodynamik, е рус. статистическа термодинамика, f pranc. термодинамична статистика, f … Fizikos terminų žodynas Клон от физиката, посветен на изследването на светлината в макроскопски план. тела, т.е. системи, състоящи се от много голям брой еднакви частици (молекули, атоми, електрони и т.н.), въз основа на връзките в тези частици и взаимодействията между тях. Изучаване на макроскопични телата са ангажирани и т.н. Физическа енциклопедия - (статистическа механика), клон на физиката, който изучава свойствата на макроскопичните тела (газове, течности, твърди тела) като системи от много голям (от порядъка на числото на Авогадро, т.е. 1023 mol 1) брой частици (молекули, атоми) , електрони). В статистически... Съвременна енциклопедия - (статистическа механика) дял от физиката, който изучава свойствата на макроскопичните тела като системи от много голям брой частици (молекули, атоми, електрони). В статистическата физика се използват статистически методи, базирани на теория на вероятностите.... ... Голям енциклопедичен речник Статистическа физика- (статистическа механика), клон на физиката, който изучава свойствата на макроскопичните тела (газове, течности, твърди тела) като системи от много голям (от порядъка на числото на Авогадро, т.е. 1023 mol 1) брой частици (молекули, атоми) , електрони). В…… Илюстрован енциклопедичен речник Съществително име, брой синоними: 2 статистики (2) физика (55) Синонимен речник на ASIS. В.Н. Тришин. 2013… Речник на синонимите СТАТИСТИЧЕСКА ФИЗИКА- глава теоретична физика, изучаване на имоти сложни системигазове, течности, твърди веществаи връзката им със свойствата на отделните частици електрони, атоми и молекули, от които са изградени тези системи. Основната задача на S. f.: намиране на функции... ... Голяма политехническа енциклопедия - (статистическа механика), клон на физиката, който изучава свойствата на макроскопичните тела като системи от много голям брой частици (молекули, атоми, електрони). В статистическата физика се използват статистически методи, базирани на теория... ... енциклопедичен речник Дял от физиката, чиято задача е да изрази свойствата на макроскопичните тела, т.е. системи, състоящи се от много голям брой еднакви частици (молекули, атоми, електрони и т.н.), чрез свойствата на тези частици и взаимодействието между тях. .. ... Велика съветска енциклопедия статистическа физика- statistinė fizika statusas T sritis fizika atitikmenys: англ. статистическа физика вок. statistische Physik, е рус. статистическа физика, f pranc. physique statistique, f … Fizikos terminų žodynas - (статистическа механика), клон на физиката, който изучава свойствата на макроскопичните материали. тела като системи от много голям брой частици (молекули, атоми, електрони). В S. f. се използват статистически методи. методи, базирани на теория на вероятностите. S. f. раздели дупката...... Естествени науки. енциклопедичен речник Статистическа термодинамика– клон на статистическата физика, който формулира закони, свързващи молекулярните свойства на веществата с експериментално измерени TD величини. STD е посветена на обосноваването на законите на термодинамиката на равновесните системи и изчисляването на функциите на TD с помощта на молекулни константи. Основата на НТР се състои от хипотези и постулати. За разлика от механиката, STL разглежда средните стойности на координатите и импулсите и вероятностите за възникване на техните стойности. Термодинамичните свойства на макроскопична система се разглеждат като средни стойности случайни променливиили като характеристики на плътност на вероятността. Има класически STD (Максуел, Болцман), квантови (Ферми, Дирак, Бозе, Айнщайн). Основната хипотеза на STD: съществува недвусмислена връзка между молекулярните свойства на частиците, които изграждат системата, и макроскопичните свойства на системата. Ансамбълът е голям, почти безкраен брой подобни TD системи, разположени в различни микросъстояния. Ансамбълът има постоянна енергиявсички микросъстояния са еднакво вероятни. Средните стойности на физически наблюдавана величина за дълъг период от време са равни на средната стойност на ансамбъла. § 1. Микро- и макросъстояния. Термодинамична вероятност (статично тегло) и ентропия. Формула на Болцман. Статистически характер на втория закон на ТД За да се опише макросъстояние, се посочва малък брой променливи (често 2). За да се опише микросъстояние, се използва описание на специфични частици, за всяка от които са въведени шест променливи. За графично представяне на микросъстояние е удобно да се използва фазово пространство. Има фазово пространство (молекули) и G-фазово пространство (газ). За да изчисли броя на микросъстоянията, Болцман използва клетъчния метод, т.е. фазовият обем е разделен на клетки и размерът на клетките е достатъчно голям, за да побере няколко частици, но малък в сравнение с целия обем. Ако приемем, че една клетка съответства на едно микросъстояние, тогава ако целият обем се раздели на обема на клетката, получаваме броя на микросъстоянията. Да приемем, че обемът на фазовото пространство е разделен на три клетки. Общ бройВ системата има девет частици. Нека едното макросъстояние е: 7+1+1, второто: 5+2+2, третото: 3+3+3. Нека преброим броя на микросъстоянията, които могат да реализират всяко макросъстояние. Този брой начини е равен на . В статистиката на Болцман частиците се считат за различими, т.е. обменът на частици между клетките дава ново микросъстояние, но макросъстоянието остава същото. Най-голямо числомикросъстоянията се дават от система, в която частиците са равномерно разпределени в целия обем. Най-нестабилното състояние съответства на натрупването на частици в една част от системата. Нека преброим броя на микросъстоянията, когато числото на Авогадро е разпределено в две клетки: Нека приложим формулата на Стърлинг: Ако една частица скочи в друга клетка, получаваме разлика от . Да вземем системата, в която е настъпил преходът хчастици. Нека искаме. Изчислението показва, че х = 10 12 . Когато системата премине към равновесно състояние, термодинамичната вероятност се увеличава значително и ентропията също се увеличава. следователно Нека намерим формата на тази функция; за това вземаме система от две клетки. В първия случай NA+0, във втория 0,5 + 0,5. Температурата е постоянна. Преходът от първото състояние към второто е изотермично разширение на газа. Според формулата на Болцман, Така се получава константата на Болцман. Сега получаваме формулата на Болцман. Да вземем две системи От две системи образуваме трета, след това ентропията нова системаще бъде равно на: Вероятността за две независими системи се умножава: Логаритмична функция: Но ентропията е размерна величина; необходим е коефициент на пропорционалност. И това е константата на Болцман. Ето един хлъзгав преход и извода, че максималната ентропия в равновесната точка не е абсолютен закон, а статистически. Както можете да видите, колкото по-малко са частиците, толкова по-рядко се изпълнява вторият закон на термодинамиката. § 2. Енергийно разпределение на молекулите. Закон на Болцман Система от H частици, . Как се разпределят молекулите в енергията? Колко молекули имат енергия? Ентропията в състояние на равновесие има максимална стойност: Сега нека намерим нещо друго: Нека намерим диференциалите: В уравнение (2) не всички величини са независими За да се отървем от зависимите променливи, използваме метода на Лагранж на неопределените множители: Те са избрани така, че коефициентите за зависимите променливи да са равни на нула. Тогава останалите членове са независими като сума. В крайна сметка се оказва, че Нека потенцираме това уравнение: Нека обобщим: Нека заместим в (3): Нека се отървем от още един множител. Уравнение (6) се логаритмира, умножава се и се сумира: Неопределеният множител на Лагранж стана определен. Накрая законът на Болцман ще бъде записан: Нека заместим стойността в (8) Коефициент на Болцман Понякога разпределението на Болцман се записва така: Съответно при температура, близка до абсолютната нула, т.е. няма молекули на възбудени нива. При температура, клоняща към безкрайност, разпределението на всички нива е еднакво. – сума по държави § 3. Сумата по състоянията на молекулата и нейната връзка с термодинамични свойства Нека разберем какви свойства има сумата от състояния на молекулата. Първо, това е безразмерна величина и нейната стойност се определя от температурата, броя на частиците и обема на системата. Това също зависи от масата на молекулата и нейната форма на движение. Освен това сумата по състояния не е абсолютна стойност; тя се определя до постоянен фактор. Стойността му зависи от нивото на отчитане на енергията на системата. Това ниво често се приема за температура абсолютна нулаи състоянието на молекулата с минимални квантови числа. Сумата по състоянията е монотонно нарастваща функция на температурата: С увеличаване на енергиите, сборът от състояния се увеличава. Сумата върху състоянията на една молекула има мултипликативното свойство. Енергията на една молекула може да бъде представена като сума от транслационна и вътрешномолекулна енергия. Тогава сумата по държави ще бъде записана по следния начин: Можете също да направите това: За вълнение електронни нивелиринеобходимо топлина. При сравнително ниски температури приносът на електронните вибрации е близо до нула. Електронно състояние на нулево ниво Всичко това се нарича приближение на Борн-Опенхаймер. Да предположим, че , тогава сумата може да бъде заменена, както следва: Ако останалите също са почти идентични един с друг, тогава: Дегенерация на нивата Тази форма на нотация се нарича сума върху енергийните нива на молекулата. Сумата от състояния е свързана с термодинамичните свойства на системата. Нека вземем производната по отношение на температурата: Получихме израз за ентропия Енергия на Хелмхолц Нека намерим налягането: Енталпия и енергия на Гибс: Оставащият топлинен капацитет е: Първо, всички количества са увеличение към нулева енергия и второ, всички уравнения са изпълнени за системи, в които частиците могат да се считат за различими. В идеалния газ молекулите са неразличими. § 4. Канонично разпределение на Гибс Гибс предложи метода на статистическите или термодинамичните ансамбли. Ансамбълът е голям, клонящ към безкрайност, брой подобни термодинамични системи, разположени в различни микросъстояния. Микроканоничният ансамбъл се характеризира с постоничност. Каноничният ансамбъл има константи. Разпределението на Болцман е получено за микроканоничния ансамбъл, нека преминем към каноничния. Каква е вероятността за едно микросъстояние в системата в термостат? Гибс въвежда концепцията за статистически ансамбъл. Нека си представим голям термостат и поставим ансамбъл в него - еднакви системи в различни микросъстояния. Позволявам М– брой системи в ансамбъла. Способен азсистеми са разположени. В каноничен ансамбъл, тъй като могат да се реализират състояния с различни енергии, трябва да очакваме, че вероятностите ще зависят от енергийното ниво, към което принадлежат. Нека има състояние, в което енергията на системата и нейната ентропия са равни. Тази система съответства на микросъстоянията. Хелмхолцовата енергия на целия ансамбъл е постоянна. Ако вътрешната енергия се приравни на енергия, тогава Тогава вероятността за едно състояние е равна на По този начин вероятностите, свързани с различни енергии, зависят от енергията на системата и тя може да бъде различна. – канонично разпределение на Гибс – вероятност за макросъстояние § 5. Сума върху състоянията на системата и връзката й с термодинамичните функции Сума по състояния на системата Функцията за състояние на системата има мултипликативното свойство. Ако енергията на системата е представена във формата: Оказа се, че тази връзка действа за система от локализирани частици. Броят на микросъстоянията за нелокализирани частици ще бъде много по-малък. Тогава: Използвайки свойството мултипликативност, получаваме: § 6. Прогресивен сбор по състояния. Ще разгледаме моноатомен идеален газ. Молекула се счита за точка, която има маса и способността да се движи в пространството. Енергията на такава частица е равна на: Такова движение има три степени на свобода, така че нека си представим тази енергия под формата на три компонента. Нека разгледаме движението по координатата х. От квантовата механика: Също така се постулира.
тъй като вероятността pminнамиране на частица в дадена клетка е равно на V 0
/
V. Ако в следващите моменти от време частицата започне да запълва по-голям обем, тогава информацията ще бъде загубена и ентропията ще се увеличи. Подчертаваме, че трябва да плащате за информация (според втория закон) чрез увеличаване на ентропията S eвъншна система и наистина, ако за един бит информация устройството (външната система) увеличи своята ентропия с количество, по-малко от един бит, тогава бихме могли да обърнем топлинния двигател. А именно, чрез разширяване на обема, зает от частица, ще увеличим нейната ентропия с количеството вътре2
получаване на работа Tln2
и общата ентропия на системата частица плюс устройство ще намалее. Но това е невъзможно според втория принцип. формално, 
, следователно намаляването на ентропията на системата (частицата) е придружено от увеличаване на ентропията на устройството.
, където (това се отнася до системи на две нива, като битове: „0“ и „1“. Ако измерението е н, Че з =
дневник n.
Да, за н
= 3, N =дневник 3
и = 3.)
Вижте какво е "СТАТИСТИЧЕСКА ТЕРМОДИНАМИКА" в други речници:
Книги
вероятно
TD свойства на едноатомен идеален газ
