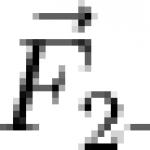Една от темите, които изискват максимално внимание и постоянство от учениците, е решаването на неравенства. Толкова подобни на уравненията и в същото време много различни от тях. Защото решаването им изисква специален подход.
Свойства, които ще са необходими за намиране на отговора
Всички те се използват за замяна на съществуващ запис с еквивалентен. Повечето от тях са подобни на това, което беше в уравненията. Но има и разлики.
- Функция, която е дефинирана в ODZ, или произволно число, може да се добави към двете страни на оригиналното неравенство.
- По същия начин умножението е възможно, но само с положителна функция или число.
- Ако това действие се извършва с отрицателна функция или число, тогава знакът за неравенство трябва да бъде заменен с противоположния.
- Функциите, които не са отрицателни, могат да бъдат повдигнати на положителна степен.
Понякога решаването на неравенства е придружено от действия, които предоставят странични отговори. Те трябва да бъдат елиминирани чрез сравняване на DL домейна и набора от решения.
Използване на метода на интервалите
Същността му е да сведе неравенството до уравнение, в което от дясната страна има нула.

- Определете областта, в която се намират допустимите стойности на променливите, т.е. ODZ.
- Преобразувайте неравенството с помощта на математически операции, така че дясната страна да има нула.
- Заменете знака за неравенство с “=” и решете съответното уравнение.
- На цифровата ос маркирайте всички отговори, получени по време на решението, както и OD интервалите. В случай на строго неравенство, точките трябва да бъдат начертани като пунктирани. Ако има знак за равенство, те трябва да бъдат боядисани.
- Определете знака на първоначалната функция на всеки интервал, получен от точките на ODZ и отговорите, които го разделят. Ако знакът на функцията не се променя при преминаване през точка, тогава тя се включва в отговора. В противен случай е изключено.
- Граничните точки за ODZ трябва да бъдат допълнително проверени и едва тогава да бъдат включени или не в отговора.
- Полученият отговор трябва да бъде написан под формата на комбинирани набори.
Малко за двойните неравенства
Те използват два знака за неравенство наведнъж. Тоест, някаква функция е ограничена от условия два пъти наведнъж. Такива неравенства се решават като система от две, когато оригиналът е разделен на части. А в интервалния метод са посочени отговорите от решаването на двете уравнения.
За разрешаването им също е допустимо да се използват свойствата, посочени по-горе. С тяхна помощ е удобно да се намали неравенството до нула.

Какво ще кажете за неравенствата, които имат модул?
В този случай решението на неравенствата използва следните свойства и те са валидни за положителна стойност на „a“.
Ако "x" вземе алгебричен израз, тогава следните замени са валидни:
- |x|< a на -a < х < a;
- |x| > от a до x< -a или х >а.
Ако неравенствата не са строги, тогава формулите също са правилни, само че в тях освен по-големия или по-малкия знак се появява "=".
Как се решава система от неравенства?
Тези знания ще са необходими в случаите, когато се дава такава задача или има запис на двойно неравенство или в записа фигурира модул. В такава ситуация решението ще бъдат стойностите на променливите, които биха задоволили всички неравенства в записа. Ако няма такива числа, системата няма решения.
Планът, според който се извършва решението на системата от неравенства:
- решавайте всеки от тях поотделно;
- изобразяват всички интервали върху числовата ос и определят техните пресечни точки;
- запишете отговора на системата, който ще бъде комбинация от случилото се във втория параграф.

Какво да правим с дробните неравенства?
Тъй като решаването им може да изисква промяна на знака на неравенството, трябва много внимателно и внимателно да следвате всички точки на плана. В противен случай може да получите обратния отговор.
Решаването на дробни неравенства също използва интервалния метод. И планът за действие ще бъде такъв:
- Използвайки описаните свойства, придайте на дроба такава форма, че да остане само нула вдясно от знака.
- Заменете неравенството с “=” и определете точките, в които функцията ще бъде равна на нула.
- Маркирайте ги върху координатната ос. В този случай числата, получени в резултат на изчисления в знаменателя, винаги ще бъдат избити. Всички останали се основават на условието за неравенство.
- Определете интервалите на постоянство на знака.
- В отговор запишете обединението на онези интервали, чийто знак съответства на този в първоначалното неравенство.
Ситуации, когато ирационалността се проявява в неравенството
С други думи, в нотацията има математически корен. Тъй като в училищен курсПо алгебра повечето от задачите са за квадратен корен, така че това ще бъде разгледано.
Решението на ирационалните неравенства се свежда до получаване на система от две или три, която ще бъде еквивалентна на оригиналната.
| Първоначално неравенство | състояние | еквивалентна система |
| √ n(x)< m(х) | m(x) по-малко или равно на 0 | няма решения |
| m(x) по-голямо от 0 | n(x) е по-голямо или равно на 0 n(x)< (m(х)) 2 |
|
| √ n(x) > m(x) | m(x) е по-голямо или равно на 0 n(x) > (m(x)) 2 |
|
n(x) е по-голямо или равно на 0 m(x) по-малко от 0 |
||
| √n(x) ≤ m(x) | m(x) по-малко от 0 | няма решения |
| m(x) е по-голямо или равно на 0 | n(x) е по-голямо или равно на 0 n(x) ≤ (m(x)) 2 |
|
| √n(x) ≥ m(x) | m(x) е по-голямо или равно на 0 n(x) ≥ (m(x)) 2 |
|
n(x) е по-голямо или равно на 0 m(x) по-малко от 0 |
||
| √ n(x)< √ m(х) | n(x) е по-голямо или равно на 0 n(x) по-малко от m(x) |
|
| √n(x) * m(x)< 0 | n(x) по-голямо от 0 m(x) по-малко от 0 |
|
| √n(x) * m(x) > 0 | n(x) по-голямо от 0 m(x) по-голямо от 0 |
|
| √n(x) * m(x) ≤ 0 | n(x) по-голямо от 0 |
|
n(x) е равно на 0 m(x) - произволен |
||
| √n(x) * m(x) ≥ 0 | n(x) по-голямо от 0 |
|
n(x) е равно на 0 m(x) - произволен |
Примери за решаване на различни видове неравенства
За да добавим яснота към теорията за решаване на неравенства, по-долу са дадени примери.
Първи пример. 2x - 4 > 1 + x
Решение: За да определите ADI, просто трябва да разгледате внимателно неравенството. Образува се от линейни функции, следователно дефиниран за всички стойности на променливата.
Сега трябва да извадите (1 + x) от двете страни на неравенството. Оказва се: 2x - 4 - (1 + x) > 0. След отваряне на скобите и задаване на подобни членове неравенството ще приеме следния вид: x - 5 > 0.
Приравнявайки го на нула, е лесно да се намери неговото решение: x = 5.
Сега тази точка с номер 5 трябва да бъде отбелязана на координатния лъч. След това проверете знаците на оригиналната функция. На първия интервал от минус безкрайност до 5 можете да вземете числото 0 и да го замените в неравенството, получено след трансформациите. След изчисления се получава -7 >0. под дъгата на интервала трябва да подпишете знак минус.
На следващия интервал от 5 до безкрайност можете да изберете числото 6. Тогава се оказва, че 1 > 0. Под дъгата има знак „+“. Този втори интервал ще бъде отговорът на неравенството.
Отговор: x се намира в интервала (5; ∞).

Втори пример. Необходимо е да се реши система от две уравнения: 3x + 3 ≤ 2x + 1 и 3x - 2 ≤ 4x + 2.
Решение. VA на тези неравенства също лежи в областта на произволни числа, тъй като са дадени линейни функции.
Второто неравенство ще приеме формата на следното уравнение: 3x - 2 - 4x - 2 = 0. След трансформация: -x - 4 =0. Това създава стойност за променливата, равна на -4.
Тези две числа трябва да бъдат маркирани на оста, изобразяващи интервали. Тъй като неравенството не е строго, всички точки трябва да бъдат защриховани. Първият интервал е от минус безкрайност до -4. Нека бъде избрано числото -5. Първото неравенство ще даде стойност -3, а второто 1. Това означава, че този интервал не е включен в отговора.
Вторият интервал е от -4 до -2. Можете да изберете числото -3 и да го замените и в двете неравенства. В първия и втория стойността е -1. Това означава, че под дъгата "-".
В последния интервал от -2 до безкрайност най-доброто число е нула. Трябва да го замените и да намерите стойностите на неравенствата. В първия от тях се оказва положително число, а втората е нула. Тази празнина също трябва да бъде изключена от отговора.
От трите интервала само един е решение на неравенството.
Отговор: x принадлежи на [-4; -2].

Трети пример. |1 - x| > 2 |x - 1|.
Решение. Първата стъпка е да се определят точките, в които функциите изчезват. За левия това число ще бъде 2, за десния - 1. Те трябва да бъдат маркирани върху лъча и да се определят интервалите на постоянство на знака.
На първия интервал, от минус безкрайност до 1, функцията от лявата страна на неравенството взема положителни стойности, а отдясно - отрицателна. Под дъгата трябва да напишете два знака „+“ и „-“ един до друг.
Следващият интервал е от 1 до 2. На него и двете функции приемат положителни стойности. Това означава, че има два плюса под дъгата.
Третият интервал от 2 до безкрайност ще даде следния резултат: лявата функция е отрицателна, дясната функция е положителна.
Като вземете предвид получените знаци, трябва да изчислите стойностите на неравенството за всички интервали.
Първо, получаваме следното неравенство: 2 - x > - 2 (x - 1). Минусът преди двете във второто неравенство се дължи на факта, че тази функция е отрицателна.
След трансформацията неравенството изглежда така: x > 0. То веднага дава стойностите на променливата. Тоест от този интервал ще се отговори само на интервала от 0 до 1.
На втория: 2 - x > 2 (x - 1). Трансформациите ще дадат следното неравенство: -3x + 4 е по-голямо от нула. Неговата нула ще бъде x = 4/3. Като се вземе предвид знакът за неравенство, се оказва, че x трябва да е по-малко от това число. Това означава, че този интервал се свежда до интервал от 1 до 4/3.
Последното дава следното неравенство: - (2 - x) > 2 (x - 1). Трансформацията му води до следното: -x > 0. Тоест, уравнението е вярно, когато x е по-малко от нула. Това означава, че на търсения интервал неравенството не дава решения.
В първите два интервала граничното число се оказа 1. Трябва да се провери отделно. Тоест, заместете го в първоначалното неравенство. Оказва се: |2 - 1| > 2 |1 - 1|. Преброяването показва, че 1 е по-голямо от 0. Това е вярно твърдение, така че единица е включена в отговора.
Отговор: x се намира в интервала (0; 4/3).
Решаване на неравенства онлайн
Преди да решавате неравенства, трябва да разберете добре как се решават уравнения.
Няма значение дали неравенството е строго () или нестрого (≤, ≥), първата стъпка е да решите уравнението, като замените знака за неравенство с равенство (=).
Нека обясним какво означава да се реши неравенство?
След изучаване на уравненията в главата на ученика се появява следната картина: той трябва да намери стойности на променливата, така че и двете страни на уравнението да приемат еднакви стойности. С други думи, намерете всички точки, в които е валидно равенството. Всичко е точно!
Когато говорим за неравенства, имаме предвид намиране на интервали (отсечки), на които е валидно неравенството. Ако има две променливи в неравенството, тогава решението вече няма да бъде интервали, а някои области на равнината. Познайте сами какво ще бъде решението на неравенство в три променливи?
Как се решават неравенства?
За универсален начин за решаване на неравенства се счита методът на интервалите (известен още като метод на интервалите), който се състои в определяне на всички интервали, в границите на които ще бъде изпълнено дадено неравенство.
Без да навлизаме в типа неравенство, в този случайтова не е въпросът, трябва да решите съответното уравнение и да определите неговите корени, последвано от обозначаването на тези решения на числовата ос.
Как правилно да напиша решението на неравенство?
След като определите интервалите за решаване на неравенството, трябва да напишете правилно самото решение. Има важен нюанс - включени ли са границите на интервалите в решението?
Тук всичко е просто. Ако решението на уравнението удовлетворява ODZ и неравенството не е строго, тогава границата на интервала се включва в решението на неравенството. В противен случай не.
Разглеждайки всеки интервал, решението на неравенството може да бъде самият интервал, или полуинтервал (когато една от неговите граници удовлетворява неравенството), или сегмент - интервалът заедно с неговите граници.
Важен момент
Не си мислете, че само интервали, полуинтервали и отсечки могат да решат неравенството. Не, решението може да включва и отделни точки.
Например неравенството |x|≤0 има само едно решение - това е точка 0.
И неравенството |x|
Защо ви е необходим калкулатор за неравенство?
Калкулаторът за неравенства дава правилния краен отговор. В повечето случаи се предоставя илюстрация на числова ос или равнина. Вижда се дали границите на интервалите са включени в решението или не - точките се показват като защриховани или пунктирани.
Благодарение на онлайн калкулаторнеравенства, можете да проверите дали правилно сте намерили корените на уравнението, отбелязали сте ги на числовата ос и сте проверили изпълнението на условието за неравенство на интервалите (и границите)?
Ако вашият отговор се различава от отговора на калкулатора, тогава определено трябва да проверите повторно решението си и да идентифицирате грешката.
Неравенството е числова връзка, която илюстрира размера на числата едно спрямо друго. Неравенствата се използват широко при търсене на количества в приложните науки. Нашият калкулатор ще ви помогне да се справите с такава трудна тема като решаването линейни неравенства.
Какво е неравенство
Неравни съотношения в реалния животса свързани с постоянното сравнение на различни обекти: по-високи или по-ниски, по-далеч или по-близо, по-тежки или по-леки. Интуитивно или визуално можем да разберем, че един обект е по-голям, по-висок или по-тежък от друг, но всъщност винаги говорим за сравняване на числа, които характеризират съответните количества. Обектите могат да се сравняват на всякакви основания и във всеки случай можем да създадем числено неравенство.
Ако неизвестните количества са равни при определени условия, тогава създаваме уравнение, за да ги определим числено. Ако не, тогава вместо знака за равенство можем да посочим всяка друга връзка между тези количества. Две числа или математически обектможе да бъде повече ">", по-малко "<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.
Знаците за неравенство в съвременната им форма са изобретени от британския математик Томас Хариот, който през 1631 г. публикува книга за неравните съотношения. Знаци по-голямо от ">" и по-малко от "<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.
Решаване на неравенства
Неравенствата, подобно на уравненията, се предлагат в различни видове. Линейни, квадратични, логаритмични или експоненциални неравенства се разрешават чрез различни методи. Въпреки това, независимо от метода, всяко неравенство трябва първо да бъде приведено до стандартна форма. За това се използват трансформации на идентичност, които са идентични с модификации на равенства.
Тъждествени преобразувания на неравенства
Такива трансформации на изрази са много подобни на призрачни уравнения, но имат нюанси, които е важно да се вземат предвид при решаването на неравенства.
Първата трансформация на идентичност е идентична на подобна операция с равенства. Едно и също число или израз с неизвестно x може да се добави или извади към двете страни на неравностойно отношение, като знакът на неравенството остава същият. Най-често този метод се използва в опростена форма като прехвърляне на членове на израз чрез знак за неравенство с промяна на знака на числото на противоположния. Това означава промяна в знака на самия термин, тоест +R, когато се прехвърли през произволен знак за неравенство, ще се промени на – R и обратно.
Втората трансформация има две точки:
- И двете страни на неравно съотношение могат да бъдат умножени или разделени на едно и също положително число. Самият знак на неравенството няма да се промени.
- И двете страни на едно неравенство могат да бъдат разделени или умножени по едно и също нещо отрицателно число. Самият знак на неравенството ще се промени на противоположния.
Второто идентично преобразуване на неравенствата има сериозни разлики с модификацията на уравненията. Първо, когато се умножава/дели с отрицателно число, знакът на неравния израз винаги се обръща. Второ, можете да разделяте или умножавате части от съотношение само с число, а не с израз, съдържащ неизвестно. Факт е, че не можем да знаем със сигурност дали едно число е по-голямо или по-малко от нула, скрито зад неизвестното, така че втората трансформация на идентичност се прилага към неравенства изключително с числа. Нека разгледаме тези правила с примери.
Примери за отприщване на неравенства
В задачите по алгебра има най-различни задачи на тема неравенства. Нека ни бъде даден изразът:
6x − 3(4x + 1) > 6.
Първо, нека отворим скобите и преместим всички неизвестни наляво и всички числа надясно.
6x − 12x > 6 + 3
Трябва да разделим двете страни на израза на −6, така че когато намерим неизвестното x, знакът за неравенство ще се промени на противоположния.
Когато решавахме това неравенство, използвахме и двете трансформации на идентичността: преместихме всички числа вдясно от знака и разделихме двете страни на отношението на отрицателно число.
Нашата програма е калкулатор на решения числови неравенства, които не съдържат неизвестни. Програмата съдържа следните теореми за връзките на три числа:
- ако А< B то A–C< B–C;
- ако A > B, тогава A–C > B–C.
Вместо да изваждате членове A-C, можете да зададете всяка аритметична операция: събиране, умножение или деление. По този начин калкулаторът автоматично ще представи неравенства за суми, разлики, произведения или дроби.
Заключение
В реалния живот неравенствата са толкова често срещани, колкото и уравненията. Естествено, знанията за разрешаване на неравенства може да не са необходими в ежедневието. В приложните науки обаче неравенствата и техните системи се използват широко. например, различни изследванияпроблемите на глобалната икономика се свеждат до компилирането и развързването на системи от линейни или квадратни неравенства, а някои неравностойни отношения служат като недвусмислен начин за доказване на съществуването на определени обекти. Използвайте нашите програми за решаване на линейни неравенства или проверете собствените си изчисления.
Днес, приятели, няма да има сополи и сантименталности. Вместо това ще ви изпратя, без въпроси, в битка с един от най-страшните противници в курса по алгебра за 8-9 клас.
Да, разбрахте всичко правилно: говорим за неравенства с модул. Ще разгледаме четири основни техники, с които ще се научите да решавате около 90% от подобни проблеми. Какво ще кажете за останалите 10%? Е, за тях ще говорим в отделен урок :)
Въпреки това, преди да анализирам някоя от техниките, бих искал да ви напомня два факта, които вече трябва да знаете. В противен случай рискувате изобщо да не разберете материала от днешния урок.
Това, което вече трябва да знаете
Captain Obviousness изглежда намеква, че за да решавате неравенства с модул, трябва да знаете две неща:
- Как се решават неравенствата;
- Какво е модул?
Да започнем с втората точка.
Дефиниция на модула
Тук всичко е просто. Има две дефиниции: алгебрична и графична. Като начало, това е алгебрично:
Определение. Модулът на число $x$ е или самото число, ако е неотрицателно, или противоположното му число, ако първоначалният $x$ все още е отрицателен.
Написано е така:
\[\ляво| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \right.\]
Говорейки на прост език, модулът е „число без минус“. И точно в тази двойственост (на някои места не е нужно да правите нищо с оригиналния номер, но на други ще трябва да премахнете някакъв вид минус) е цялата трудност за начинаещите ученици.
Има още геометрична дефиниция. Също така е полезно да се знае, но ще се обърнем към него само в сложни и някои специални случаи, където геометричният подход е по-удобен от алгебричния (спойлер: не днес).
Определение. Нека точка $a$ е отбелязана на числовата ос. След това модулът $\left| x-a \right|$ е разстоянието от точка $x$ до точка $a$ на тази права.
Ако нарисувате картина, ще получите нещо подобно:
 Дефиниране на графичен модул
Дефиниране на графичен модул По един или друг начин, от дефиницията на модул веднага следва неговото ключово свойство: модулът на числото винаги е неотрицателна величина. Този факт ще бъде червена нишка през целия ни разказ днес.
Решаване на неравенства. Интервален метод
Сега нека да разгледаме неравенствата. Има много от тях, но нашата задача сега е да можем да решим поне най-простия от тях. Такива, които се свеждат до линейни неравенства, както и до интервалния метод.
Имам два големи урока по тази тема (между другото, много, МНОГО полезни - препоръчвам да ги изучавате):
- Интервален метод за неравенства (особено гледайте видеото);
- Дробните рационални неравенства са много обширен урок, но след него няма да имате абсолютно никакви въпроси.
Ако знаете всичко това, ако фразата „да преминем от неравенство към уравнение“ не ви кара да изпитвате смътно желание да се ударите в стената, значи сте готови: добре дошли в ада в основната тема на урока :)
1. Неравенства от формата „Модулът е по-малък от функцията“
Това е един от най-честите проблеми с модулите. Необходимо е да се реши неравенство от вида:
\[\ляво| f\надясно| \ltg\]
Функциите $f$ и $g$ могат да бъдат всякакви, но обикновено са полиноми. Примери за такива неравенства:
\[\begin(align) & \left| 2x+3 \надясно| \lt x+7; \\ & \left| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0; \\ & \left| ((x)^(2))-2\left| x \right|-3 \right| \lt 2. \\\край (подравняване)\]
Всички те могат да бъдат решени буквално в един ред по следната схема:
\[\ляво| f\надясно| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \право.\право)\]
Лесно се вижда, че се отърваваме от модула, но в замяна получаваме двойно неравенство(или, което е същото, система от две неравенства). Но този преход отчита абсолютно всички възможни проблеми: ако числото под модула е положително, методът работи; ако е отрицателен, той все още работи; и дори с най-неадекватната функция на мястото на $f$ или $g$, методът пак ще работи.
Естествено възниква въпросът: не може ли да бъде по-просто? За съжаление не е възможно. Това е целият смисъл на модула.
Но стига с философстването. Нека разрешим няколко проблема:
Задача. Решете неравенството:
\[\ляво| 2x+3 \надясно| \lt x+7\]
Решение. И така, пред нас е класическо неравенство под формата „модулът е по-малък“ - дори няма какво да се трансформира. Ние работим по алгоритъма:
\[\begin(align) & \left| f\надясно| \lt g\Стрелка надясно -g \lt f \lt g; \\ & \left| 2x+3 \надясно| \lt x+7\Стрелка надясно -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]
Не бързайте да отваряте скобите, предшествани от „минус“: напълно възможно е поради бързината да направите обидна грешка.
\[-x-7 \lt 2x+3 \lt x+7\]
\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]
\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]
\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]
Задачата се сведе до две елементарни неравенства. Нека отбележим техните решения на успоредни числови прави:
Пресечна точка на множества
Пресечната точка на тези множества ще бъде отговорът.
Отговор: $x\in \left(-\frac(10)(3);4 \right)$
Задача. Решете неравенството:
\[\ляво| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]
Решение. Тази задача е малко по-трудна. Първо, нека изолираме модула, като преместим втория член надясно:
\[\ляво| ((x)^(2))+2x-3 \right| \lt -3\наляво(x+1 \надясно)\]
Очевидно отново имаме неравенство от формата „модулът е по-малък“, така че се отърваваме от модула, използвайки вече известния алгоритъм:
\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]
Сега внимание: някой ще каже, че съм малко перверзник с всички тези скоби. Но нека ви напомня още веднъж, че основната ни цел е решете правилно неравенството и получете отговора. По-късно, когато усвоите перфектно всичко, описано в този урок, можете сами да го изопачите, както желаете: отваряйте скоби, добавяйте минуси и т.н.
Като начало, просто ще се отървем от двойното минус вляво:
\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\ляво(x+1 \дясно)\]
Сега нека отворим всички скоби в двойното неравенство:
Да преминем към двойното неравенство. Този път изчисленията ще бъдат по-сериозни:
\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(align) \right.\]
\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( подравняване)\надясно.\]
И двете неравенства са квадратни и могат да бъдат решени с помощта на интервалния метод (затова казвам: ако не знаете какво е това, по-добре все още да не се заемате с модули). Нека преминем към уравнението в първото неравенство:
\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\край (подравняване)\]
Както можете да видите, резултатът е непълно квадратно уравнение, което може да бъде решено по елементарен начин. Сега нека разгледаме второто неравенство на системата. Там ще трябва да приложите теоремата на Виета:
\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\край (подравняване)\]
Отбелязваме получените числа на две успоредни линии (отделно за първото неравенство и отделно за второто):
Отново, тъй като решаваме система от неравенства, ние се интересуваме от пресечната точка на защрихованите множества: $x\in \left(-5;-2 \right)$. Това е отговорът.
Отговор: $x\in \left(-5;-2 \right)$
Мисля, че след тези примери схемата на решение е пределно ясна:
- Изолирайте модула, като преместите всички други членове в противоположната страна на неравенството. Така получаваме неравенство от вида $\left| f\надясно| \ltg$.
- Решете това неравенство, като се отървете от модула според описаната по-горе схема. В един момент ще е необходимо да се премине от двойно неравенство към система от два независими израза, всеки от които вече може да бъде решен отделно.
- И накрая, всичко, което остава, е да пресечем решенията на тези два независими израза - и това е всичко, ще получим окончателния отговор.
Подобен алгоритъм съществува за неравенства от следния тип, когато модулът е по-голям от функцията. Има обаче няколко сериозни „но“. Сега ще говорим за тези „но“.
2. Неравенства от формата „Модулът е по-голям от функцията“
Те изглеждат така:
\[\ляво| f\надясно| \gtg\]
Подобен на предишния? изглежда. И все пак такива проблеми се решават по съвсем различен начин. Формално схемата е следната:
\[\ляво| f\надясно| \gt g\Rightarrow \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]
С други думи, разглеждаме два случая:
- Първо, просто игнорираме модула и решаваме обичайното неравенство;
- След това, по същество, разширяваме модула със знака минус и след това умножаваме двете страни на неравенството по −1, докато имам знака.
В този случай опциите се комбинират с квадратна скоба, т.е. Пред нас е комбинация от две изисквания.
Моля, обърнете внимание отново: следователно това не е система, а цялост в отговора множествата са комбинирани, а не пресичащи се. Това е фундаментална разлика от предишната точка!
Като цяло, много студенти са напълно объркани със съюзите и пресичанията, така че нека разрешим този проблем веднъж завинаги:
- "∪" е знак на съюза. По същество това е стилизирана буква "U", която дойде при нас английски езики е съкращение от „Съюз“, т.е. „Асоциации“.
- „∩“ е знакът за пресичане. Тези глупости не идват отникъде, а просто се появяват като контрапункт на „∪“.
За да направите запомнянето още по-лесно, просто нарисувайте крака към тези знаци, за да направите очила (само не ме обвинявайте сега, че насърчавам наркоманиите и алкохолизма: ако изучавате сериозно този урок, значи вече сте наркоман):
 Разлика между пресичане и обединение на множества
Разлика между пресичане и обединение на множества Преведено на руски това означава следното: съюзът (съвкупността) включва елементи от двете множества, следователно по никакъв начин не е по-малък от всеки от тях; но пресечната точка (системата) включва само тези елементи, които са едновременно както в първото множество, така и във второто. Следователно пресечната точка на множествата никога не е по-голяма от изходните множества.
Значи стана по-ясно? това е страхотно Да преминем към практиката.
Задача. Решете неравенството:
\[\ляво| 3x+1 \надясно| \gt 5-4x\]
Решение. Продължаваме по схемата:
\[\ляво| 3x+1 \надясно| \gt 5-4x\дясна стрелка \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ точно.\]
Решаваме всяко неравенство в популацията:
\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]
\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]
\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]
Маркираме всеки получен набор на числовата линия и след това ги комбинираме:
Обединение на комплекти
Съвсем очевидно е, че отговорът ще бъде $x\in \left(\frac(4)(7);+\infty \right)$
Отговор: $x\in \left(\frac(4)(7);+\infty \right)$
Задача. Решете неравенството:
\[\ляво| ((x)^(2))+2x-3 \right| \gt x\]
Решение. добре? Нищо - всичко е същото. Преминаваме от неравенство с модул към набор от две неравенства:
\[\ляво| ((x)^(2))+2x-3 \right| \gt x\Rightarrow \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \right.\]
Решаваме всяко неравенство. За съжаление, корените там няма да са много добри:
\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\&D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\край (подравняване)\]
Второто неравенство също е малко диво:
\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\&D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\край (подравняване)\]
Сега трябва да маркирате тези числа на две оси - по една ос за всяко неравенство. Трябва обаче да маркирате точките в правилния ред: отколкото по-голям брой, колкото повече изместваме точката надясно.
И тук ни очаква настройка. Ако всичко е ясно с числата $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (членовете в числителя на първия дроб са по-малки от членовете в числителя на втория, така че сумата също е по-малка), с числата $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ също няма да има затруднения (положителното число очевидно е по-отрицателно), тогава с последната двойка всичко не е толкова ясно. Кое е по-голямо: $\frac(-3+\sqrt(21))(2)$ или $\frac(-1+\sqrt(13))(2)$? Разположението на точките върху числовите оси и всъщност отговорът ще зависи от отговора на този въпрос.
Така че нека сравним:
\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrix)\]
Изолирахме корена, получихме неотрицателни числа от двете страни на неравенството, така че имаме право да поставим на квадрат и двете страни:
\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \ 4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]
Мисля, че е безсмислено, че $4\sqrt(13) \gt 3$, така че $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, крайните точки на осите ще бъдат поставени така:
Случай на грозни корени
Нека ви напомня, че решаваме колекция, така че отговорът ще бъде обединение, а не пресичане на защриховани множества.
Отговор: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty \right)$
Както можете да видите, нашата схема работи чудесно както за прости, така и за много трудни проблеми. Единственото „слабо място“ в този подход е, че трябва да сравнявате правилно ирационални числа(и повярвайте ми: не са само корените). Но отделен (и много сериозен) урок ще бъде посветен на проблемите на сравнението. И продължаваме напред.
3. Неравенства с неотрицателни „опашки“
Сега стигаме до най-интересната част. Това са неравенства от вида:
\[\ляво| f\надясно| \gt\наляво| g\надясно|\]
Най-общо казано, алгоритъмът, за който ще говорим сега, е правилен само за модула. Работи във всички неравенства, където има гарантирани неотрицателни изрази отляво и отдясно:
Какво да правим с тези задачи? Просто запомни:
В неравенства с неотрицателни „опашки“ и двете страни могат да бъдат повдигнати на всяка естествена степен. Няма да има допълнителни ограничения.
На първо място, ще се интересуваме от квадратурата - тя изгаря модули и корени:
\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\край (подравняване)\]
Просто не бъркайте това с вземане на корен от квадрат:
\[\sqrt(((f)^(2)))=\left| f \right|\ne f\]
Безброй грешки бяха направени, когато ученик забрави да инсталира модул! Но това е съвсем различна история (това са, така да се каже, ирационални уравнения), така че няма да навлизаме в това сега. Нека решим по-добре няколко проблема:
Задача. Решете неравенството:
\[\ляво| x+2 \right|\ge \left| 1-2x \right|\]
Решение. Нека веднага да отбележим две неща:
- Това не е строго неравенство. Точките на числовата ос ще бъдат пробити.
- И двете страни на неравенството очевидно са неотрицателни (това е свойство на модула: $\left| f\left(x \right) \right|\ge 0$).
Следователно можем да повдигнем на квадрат двете страни на неравенството, за да се отървем от модула и да решим проблема, използвайки обичайния метод на интервала:
\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\край (подравняване)\]
На последната стъпка изневерих малко: промених последователността от членове, като се възползвах от четността на модула (всъщност умножих израза $1-2x$ по −1).
\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ дясно)\дясно)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]
Решаваме с помощта на интервалния метод. Нека преминем от неравенство към уравнение:
\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\край (подравняване)\]
Отбелязваме намерените корени на числовата ос. Още веднъж: всички точки са защриховани, защото първоначалното неравенство не е строго!
Отървете се от знака за модул
Нека напомня за тези, които са особено упорити: вземаме знаците от последното неравенство, което беше написано преди да преминем към уравнението. И рисуваме върху площите, изисквани в същото неравенство. В нашия случай това е $\left(x-3 \right)\left(3x+1 \right)\le 0$.
Е, това е всичко. Проблемът е решен.
Отговор: $x\in \left[ -\frac(1)(3);3 \right]$.
Задача. Решете неравенството:
\[\ляво| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \right|\]
Решение. Правим всичко по същия начин. Няма да коментирам - просто вижте последователността на действията.
Квадратирайте го:
\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left |. ((x)^(2))+3x+4 \right|)^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \десен))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ надясно))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]
Интервален метод:
\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Стрелка надясно x=-1.5; \\ & 2((x)^(2))+4x+5=0\Стрелка надясно D=16-40 \lt 0\Стрелка надясно \varnothing . \\\край (подравняване)\]
На числовата ос има само един корен:
Отговорът е цял интервал
Отговор: $x\in \left[ -1.5;+\infty \right)$.
Малка забележка за последната задача. Както един от моите ученици точно отбеляза, и двата подмодулни израза в това неравенство са очевидно положителни, така че знакът за модул може да бъде пропуснат без вреда за здравето.
Но това е съвсем друго ниво на мислене и друг подход – условно може да се нарече метод на следствията. За това - в отделен урок. Сега нека преминем към последната част от днешния урок и да разгледаме един универсален алгоритъм, който винаги работи. Дори когато всички предишни подходи бяха безсилни. :)
4. Метод на изброяване на опциите
Ами ако всички тези техники не помогнат? Ако неравенството не може да бъде сведено до неотрицателни опашки, ако е невъзможно да се изолира модулът, ако като цяло има болка, тъга, меланхолия?
Тогава на сцената излиза „тежката артилерия“ на цялата математика – методът на грубата сила. Във връзка с неравенства с модул изглежда така:
- Изпишете всички подмодулни изрази и ги задайте равни на нула;
- Решете получените уравнения и маркирайте намерените корени на една числова ос;
- Правата линия ще бъде разделена на няколко секции, в рамките на които всеки модул има фиксиран знак и следователно се разкрива уникално;
- Решете неравенството на всеки такъв участък (можете отделно да разгледате корените-граници, получени в стъпка 2 - за надеждност). Комбинирайте резултатите - това ще бъде отговорът. :)
Е как? слаб? лесно! Само за дълго време. Да видим на практика:
Задача. Решете неравенството:
\[\ляво| x+2 \надясно| \lt \наляво| x-1 \right|+x-\frac(3)(2)\]
Решение. Тези глупости не се свеждат до неравенства като $\left| f\надясно| \lt g$, $\left| f\надясно| \gt g$ или $\left| f\надясно| \lt \наляво| g \right|$, така че действаме напред.
Изписваме подмодулни изрази, приравняваме ги към нула и намираме корените:
\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\Стрелка надясно x=1. \\\край (подравняване)\]
Общо имаме два корена, които разделят числовата линия на три секции, в които всеки модул се разкрива уникално:
Разделяне на числовата ос с нули на подмодулни функции
Нека разгледаме всеки раздел поотделно.
1. Нека $x \lt -2$. Тогава и двата подмодулни израза са отрицателни и оригиналното неравенство ще бъде пренаписано, както следва:
\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1.5 \\ & -x-2 \lt -x+1+ x- 1.5 \\ & x \gt 1.5 \\\end(align)\]
Имаме доста просто ограничение. Нека го пресечем с първоначалното предположение, че $x \lt -2$:
\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1.5 \\\end(align) \right.\Rightarrow x\in \varnothing \]
Очевидно променливата $x$ не може да бъде едновременно по-малка от −2 и по-голяма от 1,5. В тази област няма решения.
1.1. Нека разгледаме отделно граничния случай: $x=-2$. Нека просто заместим това число в първоначалното неравенство и да проверим: вярно ли е?
\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=-2) ) \ \ & 0 \lt \left| -3\дясно|-2-1,5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0.5\Стрелка надясно \varnothing . \\\край (подравняване)\]
Очевидно е, че веригата от изчисления ни е довела до неправилно неравенство. Следователно първоначалното неравенство също е невярно и $x=-2$ не е включено в отговора.
2. Нека сега $-2 \lt x \lt 1$. Левият модул вече ще се отвори с „плюс“, но десният все още ще се отвори с „минус“. Ние имаме:
\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\край (подравняване)\]
Отново се пресичаме с първоначалното изискване:
\[\left\( \begin(align) & x \lt -2.5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]
И отново, множеството от решения е празно, тъй като няма числа, които да са едновременно по-малки от −2,5 и по-големи от −2.
2.1. И отново специален случай: $x=1$. Заменяме в първоначалното неравенство:
\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \ляво| 3\надясно| \lt \наляво| 0 \right|+1-1.5; \\ & 3 \lt -0,5; \\ & 3 \lt -0.5\Стрелка надясно \varnothing . \\\край (подравняване)\]
Подобно на предишния „специален случай“, числото $x=1$ очевидно не е включено в отговора.
3. Последната част от реда: $x \gt 1$. Тук всички модули се отварят със знак плюс:
\[\begin(align) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\ ]
И отново пресичаме намереното множество с оригиналното ограничение:
\[\left\( \begin(align) & x \gt 4.5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4.5;+\infty \right)\ ]
Е, най-накрая! Намерихме интервал, който ще бъде отговорът.
Отговор: $x\in \left(4,5;+\infty \right)$
И накрая, една бележка, която може да ви спаси от глупави грешкипри решаване на реални проблеми:
Решенията на неравенства с модули обикновено представляват непрекъснати множества на числовата ос - интервали и отсечки. Изолираните точки са много по-рядко срещани. И още по-рядко се случва границата на решението (края на сегмента) да съвпада с границата на разглеждания диапазон.
Следователно, ако границите (същите „специални случаи“) не са включени в отговора, тогава областите отляво и отдясно на тези граници почти сигурно няма да бъдат включени в отговора. И обратното: границата, въведена в отговора, което означава, че някои области около нея също ще бъдат отговори.
Имайте това предвид, когато преглеждате вашите решения.
В статията ще разгледаме решаване на неравенства. Ще ви кажем ясно за как да се конструира решение на неравенства, с ясни примери!
Преди да разгледаме решаването на неравенства с помощта на примери, нека разберем основните понятия.
Общи сведения за неравенствата
Неравенствое израз, в който функциите са свързани със знаци за релация >, . Неравенствата могат да бъдат както числови, така и буквални.
Неравенствата с два знака на съотношението се наричат двойни, с три - тройни и т.н. Например:
a(x) > b(x),
a(x) a(x) b(x),
a(x) b(x).
a(x) Неравенствата, съдържащи знака > или или - не са строги.
Решаване на неравенствотое всяка стойност на променливата, за която това неравенство ще бъде вярно.
"Решете неравенство" означава, че трябва да намерим множеството от всички негови решения. Има различни методи за решаване на неравенства. За решения за неравенстваТе използват числовата линия, която е безкрайна. например, решение на неравенството x > 3 е интервалът от 3 до +, а числото 3 не е включено в този интервал, следователно точката на правата е означена с празен кръг, т.к. неравенството е строго. +
Отговорът ще бъде: x (3; +).
Стойността x=3 не е включена в набора от решения, така че скобите са кръгли. Знакът за безкрайност винаги се подчертава със скоба. Знакът означава "принадлежност".
Нека да разгледаме как се решават неравенства, използвайки друг пример със знак:
х 2
-+
Стойността x=2 е включена в набора от решения, така че скобата е квадратна и точката на линията е обозначена със запълнен кръг.
Отговорът ще бъде: x)