Въпроси относно кинематиката

Въведение в кинематиката

1. Какво изучава кинематиката?

2. Отправно тяло, координатна система, отправна система.

3. Пространство и време в кинематиката.

4. Какви свойства е надарен с кинематичната точка?

5. Проблеми на кинематиката.

I. Кинематика на точка

1. Какво означава „задаване на движението“? Избройте начините за определяне на движение.

2. Векторен метод за определяне на движението на точка.

3. Траектория на точка, концепция за праволинейни и криволинейни движения на точка.

4. Векторът на скоростта на точка, векторът на ускорението на точка с векторния метод за определяне на движението. Векторът на скоростта на точка като производна на радиус вектора на точката. Векторът на ускорението на точка като първа производна на вектора на скоростта на точката. Мерни единици на модулите на вектора на скоростта и вектора на ускорението.

5. Как са насочени векторът на скоростта и векторът на ускорението на точка по отношение на траекторията, когато се използва векторният метод за определяне на движение? Концепцията за ускорено и забавено движение.

6. Координатен метод за уточняване на движението на точка.

7. Траектория на точка, проекции на вектора на скоростта и вектора на ускорението на точката с координатния метод за определяне на движението на точката.

8. Определяне на векторния модул на скоростта и векторния модул на ускорението от техните проекции.

9. Връзка между векторни и координатни методи за определяне на движение.

10. Естествен начин за уточняване на движението на точка. Естествени оси. Кривина и радиус на кривина на траекторията (елементарна информация от геометрията на пространствената крива).

11. Определяне на алгебричната скорост на точка при задаване на нейното движение по естествен начин. Как може да се прецени посоката на движение на точка по траектория по знака на алгебричната скорост?

12. Разлагане на вектора на ускорението на тангенциална и нормална компоненти. Формули за определяне на алгебричните величини на тангенциалните и нормалните ускорения.

13. Определяне на модула на вектора на ускорението на точка (общо ускорение на точката) от известните стойности на допирателната и нормалните ускорения на точката.

14. Най-простите закони за движение на точка по траектория с естествен начин за определяне на движението.

II. Постъпателно движение на твърдо тяло и въртене на твърдо тяло около неподвижна ос

1. Постъпателно движение на твърдо тяло, определение. Основната теорема за постъпателното движение на тялото.

2. Как се определя законът за постъпателното движение на твърдо тяло.

3. Въртене на твърдо тяло около неподвижна ос. Уравнение на въртене на твърдо тяло около неподвижна ос.

3. Ъглова скорост и ъглово ускорение на твърдо тяло като алгебрични величини. Единици за измерване на ъглова скорост и ъглово ускорение.

4. Закон (уравнение) за равномерно въртеливо движение на тяло. Законът (уравнение) за равномерно въртене на тяло около фиксирана ос.

7. Стойностите на тангенциалното, нормалното и пълното ускорение на точка на тяло, въртящо се около фиксирана ос.

8. Ъглова скорост и ъглово ускорение на тяло като вектори. Как са насочени тези вектори един спрямо друг по време на ускорено и забавено въртене на тялото?

9. Изразяване на вектора на скоростта на точка от тяло, въртяща се около неподвижна ос, под формата на векторно произведение.

10. Изразяване на вектори на тангенциални и нормални ускорения на точка от тяло, въртящо се около неподвижна ос, под формата на векторни произведения.

III. Плоскопаралелно (равнинно) движение на твърдо тяло

1. Определение за равнинно движение на твърдо тяло.

2. Закон за движение (уравнения) на равнинно движение на твърдо тяло.

2. Разлагане на движението на равнинна фигура на транслационно и въртеливо движение чрез анализ на уравненията на равнинното движение.

3. Теорема за геометричното събиране на вектори на скоростта на точки от равнинна фигура. Проекционен метод.

4. Теорема за проекциите на скоростите на две точки от тяло.

5. Концепцията за моментния център на скоростите на плоска фигура. Определяне на положението на моментния център на скоростта в общия случай.

6. Определяне на скоростите на точки от плоска фигура с помощта на моментния център на скоростите.

7. Частни случаи на определяне на положението на центъра на моментната скорост.

8. Теорема за геометричното събиране на вектори на ускорение на точки от равнинна фигура. Проекционен метод.

VI. Сложно точково движение

1. Сложно точково движение - определение. Относително движение на точка, относителна траектория, относителна скорост и ускорение на точка.

2. Преносимо движение на точката. Преносими точки за скорост и ускорение.

3. Абсолютно движение на точка, абсолютна траектория, абсолютна скорост и ускорение на точка.

4. Теорема за добавяне на вектори на скоростта при абсолютното движение на точка. Проекционен метод.

5. Теорема за добавяне на вектори на ускорение при сложно движение на точка (теорема на Кориолис). Проекционен метод.

6. Големина и посока на вектора на Кориолисовото ускорение.

7. Специални случаи, при които кориолисовото ускорение е равно на нула.

8. Физически причини, предизвикващи Кориолисово ускорение.

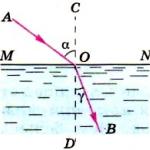
Досега при изучаване на движението на точка (отделна точка, точка от тяло) винаги сме приемали, че координатната система Oxyz, спрямо която се разглежда движението, е неподвижна. Сега да разгледаме случая, когато координатната система Oxyz също се движи, така че се движат както точката M, така и координатната система Oxyz - спрямо друга координатна система, която е неподвижна (фиг. 111). Този случай, когато движението на точка М се разглежда едновременно в две координатни системи - подвижна и неподвижна, се нарича комплексно движение на точката.

Преместването на точка спрямо фиксирана координатна система се нарича абсолютно движение. Скоростта и ускорението му спрямо неподвижните оси се наричат ​​съответно абсолютна скорост и абсолютно ускорение.

Преместването на точка спрямо движеща се координатна система се нарича относително движение.

Скоростта и ускорението на точка по отношение на движещите се оси се наричат ​​относителна скорост (обозначено) и относително ускорение. Индекс – от латинската дума relativus (роднина).

Движението на подвижна координатна система, заедно с геометрични точки, неизменно свързани с нея, спрямо фиксирана координатна система се нарича преносимо движение. Преносимата скорост и преносимото ускорение на точка M са скоростта и ускорението спрямо неподвижната координатна система на точка M, неизменно свързана с подвижните оси, с които движещата се точка M съвпада в даден момент от времето.Индексът e е от латинското enteiner (нося със себе си).

Понятията скорост на трансфер и ускорение на трансфер са по-фини. Нека предоставим следното допълнително обяснение. В процеса на относително движение точка М се намира на различни места (точки) от подвижната координатна система.

Нека означим с М точката от подвижната координатна система, с която в момента съвпада подвижната точка М. Точка М се движи заедно с подвижната координатна система спрямо неподвижната система с определена скорост и ускорение. Тези количества служат като преносима скорост и преносимо ускорение на точка М:

Нека направим още два коментара.

1. Подвижните и фиксирани координатни оси, които се появяват при формулирането на проблема със сложното движение, са необходими само за общото формулиране на проблема. На практика ролята на координатни системи изпълняват конкретни тела и обекти – подвижни и неподвижни.

2. Преносимото движение или, което е същото, движението на движещи се оси спрямо неподвижни, се свежда до едно от движенията на твърдо тяло - транслационно, ротационно и др. Следователно, когато изчислявате преносимата скорост и преносимото ускорение, трябва да използвате подходящите правила, установени за различни видове движение на тялото.

Скоростите и ускоренията при сложно движение са свързани със строги математически зависимости - теорема за събиране на скоростите и теорема за събиране на ускорения.

Равнопаралелно движение на твърдо тяло.

1. Уравнения на плоскопаралелно движение

Плоскопаралелен (или плосък) е движението на твърдо тяло, при което всички негови точки се движат успоредно на някаква фиксирана равнина P.

Нека разгледаме сечението S на тялото с някаква равнина Оxy, успоредна на равнината П. При равнинно-паралелно движение всички точки на тялото лежат на права линия MM / , перпендикулярно на сечението (С) , тоест към самолета П се движат еднакво и във всеки момент имат еднакви скорости и ускорения. Следователно, за да се изследва движението на цялото тяло, е достатъчно да се проучи как се движи секцията С тела в равнина Оxy.

Уравнения (4.1) определят закона на протичащото движение и се наричат уравнения на плоскопаралелно движение на твърдо тяло.

2. Разлагане на плоскопаралелно движение на постъпателно движение

заедно с полюса и се върти около полюса

Нека покажем, че равнинното движение се състои от транслационно и въртеливо движение. За да направите това, разгледайте две последователни позиции I и II, които секцията заема Сдвижещо се тяло в моменти от време т 1 И t 2= t 1 + Δt . Лесно се вижда, че секцията С, а с него цялото тяло може да бъде приведено от позиция I до позиция II по следния начин: първо преместваме тялото транслационно, така че полюсът А, движейки се по траекторията си, стигна до позиция А 2. В този случай сегментът A 1 B 1ще заеме позиция и след това ще завърти секцията около полюса А 2под ъгъл Δφ 1.

Следователно равнинно-паралелното движение на твърдо тяло се състои от транслационно движение, при което всички точки на тялото се движат по същия начин като полюса А също и от въртеливото движение около този полюс.

Трябва да се отбележи, че въртеливото движение на тялото се извършва около ос, перпендикулярна на равнината П и преминавайки през полюса А. Но за краткост оттук нататък ще наричаме това движение просто въртене около полюса А.

Постъпателната част на равнинно-паралелното движение очевидно се описва от първите две от уравненията (2.1), а въртенето около полюса А -третото от уравненията (2.1).

Основни кинематични характеристики на равнинното движение

Можете да изберете всяка точка от тялото като полюс

Заключение : ротационният компонент на равнинното движение не зависи от избора на полюс, следователно ъгловата скоростω и ъглово ускорениедса общи за всички полюси и се наричатъглова скорост и ъглово ускорение на равнинна фигура

Векторите и са насочени по ос, минаваща през полюса и перпендикулярна на равнината на фигурата

3D изображение

3. Определяне на скоростите на точките на тялото

Теорема: скоростта на всяка точка от равнинна фигура е равна на геометричната сума от скоростта на полюса и скоростта на въртене на тази точка около полюса.

В доказателството ще изхождаме от факта, че плоскопаралелното движение на твърдо тяло се състои от постъпателно движение, при което всички точки на тялото се движат със скорост vАи от въртеливото движение около този полюс. За да разделим тези два вида движение, въвеждаме две отправни системи: Oxy – стационарна и Ox 1 y 1 – движеща се транслационно заедно с полюса А.Спрямо движещата се отправна система, движението на точка Мще се „върти около полюса А».

По този начин скоростта на която и да е точка M от тялото геометрично е сумата от скоростта на друга точка А, взета като полюс, и скоростта на точката Мвъв въртеливото си движение заедно с тялото около този полюс.

Геометрична интерпретация на теоремата

Следствие 1. Проекциите на скоростите на две точки от твърдо тяло върху права линия, свързваща тези точки, са равни една на друга.

Този резултат улеснява намирането на скоростта на дадена точка от тялото, ако са известни посоката на движение на тази точка и скоростта на друга точка от същото тяло.

Плоско (плоскопаралелно) движение на твърдо тяло е такова движение на тяло, при което всички негови точки се движат в равнини, успоредни на някаква фиксирана равнина.

Равнинното движение на твърдо тяло може да се разложи на транслационно движение на тялото заедно с определена точка на тялото (полюс) и въртене около ос, минаваща през полюса, перпендикулярен на равнината на движение.

Броят на степените на свобода при равнинно движение е три. Да изберем точка А на тялото – полюса. Две координати ще определят движението на полюса, а третата ще определи ъгъла на въртене - въртене около полюса:

,
,
.

Последните изрази се наричат ​​уравнения на равнинното движение на твърдо тяло.

3.2. Скорости на точките на тялото при равнинно движение.

Моментален център на скоростта

Обмислете точките АИ INтвърдо тяло, подложено на равнинно движение. Радиус векторна точка IN
,
, тъй като това е разстоянието между две точки в твърдо тяло. Нека разграничим двете страни на това равенство:
или
. За
Нека приложим формулата за производната на вектор с постоянен модул:

– точкова скорост INкогато тялото се върти около полюс А. Тогава,
или
, Където – вектор на ъгловата скорост на тялото, той е насочен по оста, минаваща през точката Аперпендикулярно на равнината на движение. Модул – от ABлежи в равнина и перпендикулярна на равнината.

Моментният център на скоростите на тялото при равнинно движение е точката на тялото или движеща се равнина, твърдо свързана с тялото, чиято скорост в даден момент от времето е нула.

Нека покажем, че ако в даден момент от време ъгловата скорост на тялото
, тогава съществува моментен център на скоростта. Помислете за плоска фигура, движеща се в чертожната равнина,
, точкова скорост А–. Нека начертаем перпендикуляр на Ада ускоря и поставете сегмент върху него
. Нека покажем това Р– моментен център на скоростите, т.е.
.

Точкова скорост Р
,
, т.е.
, следователно
, което означава Р– моментен център на скоростите.

Нека сега тялото извършва равнинно движение и положението на моментния център на скоростите е известно Р. Нека първо определим скоростта на точката А:,
; точкова скорост IN:
; Тогава
. Следователно скоростите на точките на едно тяло при равнинно движение са свързани като техните разстояния до моментния център на скоростите.

Нека разгледаме начини за намиране на моментния център на скоростите.

3.3. Ускорение на точките на тялото по време на равнинно движение.

Център за незабавно ускоряване

Обмислете точките АИ INтвърдо тяло, подложено на равнинно движение. Точкова скорост IN
. Нека разграничим двете страни на това равенство:
. Нека обозначим
,
,
– ъглово ускорение,
– точкова скорост INспрямо полюса А,. Нека въведем следната нотация:
– тангенциално (въртеливо) ускорение на точка IN, когато тялото се върти около полюса А,– вектор на ъглово ускорение, насочен перпендикулярно на равнината на движение; – нормално ускорение на точката бкогато тялото се върти около полюс А. Използвайки тези обозначения, изразът за ускорение се записва, както следва:
. По този начин ускорението на всяка точка на тялото по време на равнинно движение е равно на геометричната сума от ускорението на всяка друга точка на тялото (полюс) и ускорението на точка на тялото по време на въртенето му около полюса. Ако обозначим
, Че
,
,
,
.

Моментният център на ускорение на тялото по време на равнинно движение е точка от тялото или подвижна равнина, твърдо свързана с тялото, чието ускорение в даден момент от време е нула.

Нека покажем, че ако в даден момент от времето
И
, тогава съществува моментен център на ускорение. Помислете за плоска фигура, движеща се в чертожната равнина,
,
точково ускорение А–
. Нека изпълним в точката Аъглова греда
да забързаш
и поставете сегмент върху него
. Нека покажем това Q– моментен център на ускорение, т.е.
.

Точково ускорение Q
,

,
,
,
, следователно
, което означава Q– моментен център на ускорението. Тогава
,
,
.

Нека разгледаме начините за определяне на ъгловото ускорение на тялото при равнинно движение.

1. Ако ъгълът на завъртане е известен
, Че
.

2. Проектиране на векторно уравнение
върху ос, перпендикулярна на ускорението на точката IN(с познати , посока и величина
, векторна посока
), получаваме уравнение, от което определяме
и тогава
.