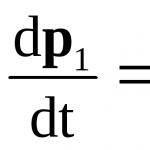За да използвате визуализации на презентации, създайте акаунт в Google и влезте в него: https://accounts.google.com
Надписи на слайдове:
ПРОИЗВОДНА НА ЕКСПОНЕНЦИАЛНА ФУНКЦИЯ Число д 11 клас
ПОВТОРЕНИЕТО е майката на ученето!
Определение експоненциална функцияфункция, дадено от формулата y = a x (където a > 0, a ≠ 1) се нарича експоненциална функция с основа a.
Свойства на експоненциалната функция y = a x a>1 0
Определяне на производната на функция в точка x 0. като Δ → 0. Производната на функцията f в точката x 0 е числото, към което съотношението на разликата клони при Δx → 0.
Геометрично значение на производната x ₀ α A y = f(x) 0 x y к = tan α = f "(x ₀) Коефициентът на ъгъл към допирателната към графиката на функцията f (x) в точката (x 0 ; f (x 0) е равно на производните функции f "(x ₀). f(x 0)
Игра: „Намерете двойките“ (u + v)" cos x e (u v)" n xⁿ ⁻" p (u / v)" - 1 /(sin² x) a (x ⁿ)" - sin x n C "u" v +u v" до (C u)" 1 / (cos ² x) t (sin x)" (u" v – u v") / v² c (cos x)" 0 o (tg x)" u " + v " e (ctg x) " C u " n
Проверете себе си! (u + v)" u" + v" e (u v)" u" v + u v " до (u /v)" (u' v –u v") / v² s (x ⁿ)" n x ⁿ ⁻¹ p C" 0 o (Cu)" C u " n (sin x)" Cos x e (cos x)" - sin x n (tg x)" 1 / (cos² x) t (ctg x)" - 1 / (sin² x ) а
Експоненциалът е степенна функция. Показателят е функция, където e е основата на естествените логаритми.
1 y= e x 45° Функцията y= e x се нарича „експонента” x ₀ =0; tg 45° = 1 В точка (0;1) наклонът към допирателната към графиката на функцията k = tg 45° = 1 - геометричен смисълпроизводна на показателя Показател y = e x
Теорема 1. Функцията y = e е диференцируема във всяка точка от областта на дефиниция и (e)" = e x x x Натуралният логаритъм (ln) е логаритъмът при основа e: ln x = log x e Експоненциалната функция е диференцируема във всяка точка от областта на дефиницията и (a)" = a ∙ ln a x x Теорема 2.
Формули за диференциране на експоненциалната функция (e)" = e ; (e)" = k e ; (a)" = a ∙ ln a; (a)" = k a ∙ ln a. x kx + b x x x kx + b kx + b kx + b F(a x) = + C; F(e x) = e x +C.
„Упражнението поражда майсторство.“ Тацит Публий Корнелий - древноримски историк
Примери: Намерете производните на функциите: 1. = 3 e. 2. (e)" = (5x)" e = 5 e. 3. (4)" = 4 ln 4. 4. (2)" = (-7 x)" 2 ∙ ln 2 = -7 ∙ 2 ∙ ln 2. 5 x 5 x x (3 e)" 5 x - 7 x x x -7 x -7 x x
Интересни неща наблизо
Леонхард Ойлер 1707 -1783 Руски учен - математик, физик, механик, астроном... Въвежда означението за числото е. Доказва, че числото е ≈ 2, 718281... е ирационално. Джон Напиер 1550 – 1617 Шотландски математик, изобретател на логаритмите. В негова чест числото e се нарича „числото на Непер“.
Нарастването и затихването на функция с експоненциална скорост се нарича експоненциално

Учител по математика MOU
"Мултановска гимназия"
Маханова Самига Галимжановна
с. М у л т а н о в о
февруари 2011 г
Тема на урока:"Числото e. Производна на експоненциална функция."
Мишена:Въведете концепцията за „експонента“, „естествен логаритъм“, формирайте концепцията за производната на експоненциалната функция y = e x, антипроизводната на експоненциалната функция.
Образователни:
Повторете и задълбочете знанията си по темата „Експоненциална функция. Свойства на експоненциалната функция“;
Повторете правилата за разграничаване на функция;
Запознайте учениците с понятието „експоненти“ (числа e);
Запознайте учениците с формулите за производната на показателната функция y = А х и y = a kx +b ;
Въвеждане на формулата на експоненциалната функция на първообразната;
Развийте умения за изчисляване на производната на експоненциална функция, като използвате правилата и формулите за диференциране.
Развитие:
Разработване и подобряване на прилагането на правилата за диференциация
за експоненциална функция;
Научете учениците да използват електроника информационни технологиипри преподаване и подготовка за часовете по математика.
Подобряване на графичната култура на учениците;
Да насърчава развитието на умения за извършване на самооценка на образователните дейности.
Образователни:
Създайте положителна мотивация на учениците в часовете по математика, като включите всички в активни дейности;
Насърчавайте необходимостта да оценявате собствените си дейности и работата на вашите другари;
Помогнете да разберете ценностите на работата в екип;
Да се култивира точността и културата на математическата реч у учениците.
Оборудване за урока:
Компютърен клас (8 лаптопа +1 лаптоп за демонстрация), проектор, презентация, раздатъчни материали.
По време на часовете:
Организация на урока, обявяване на темата и целта на урока:
Днес в клас учим нова тема"Производна на експоненциална функция." Нашата цел: (Слайд 2.) да се запознаем с понятието „показател“, „естествен логаритъм“, с теоремата за диференцирането на показателната функция и да научим как да диференцираме показателната функция.
Избрах стиховете на Б. Слуцки като епиграф за нашия урок: (слайд 3.)
…Експоненциална функция
Не случайно съм роден
Органично интегриран в живота
И поех движението на прогреса.
Б. Слуцки
азАктуализиране на основни знания:
Устна фронтална работа с класа:
Формулирайте дефиницията на експоненциалната функция (Слайд 5.)
Избройте основните свойства на експоненциалната функция с помощта на графика.
(Слайд 6)
Свойства на експоненциалната функция:(слайд 4)
Функционален домейн
Обхват на експоненциална функция
Графиката на функцията с op оста се пресича в точката (0;1) и не се пресича с оста OX.
Експоненциалната функция отнема положителни стойностина цялата числова ос.
Избройте свойствата на експоненциалната функция за a 1.
Избройте свойствата на експоненциалната функция при 0 .
Дефинирайте производната на функция в точка x 0 . (слайд 7)
Формулирайте геометричния смисъл на производната. (слайд 8)
Сега нека си припомним правилата за разграничаване на функциите:
2) Игра „Намерете двойките“. (слайд 9.)
За формули от първата колона намерете верните отговори от втората колона и прочетете думата от третата колона. Устно, с коментар.
| (u +v)" | cos x | д |
| (u v)" | n x n-1 | П |
| (u/v)" | -1/sin2x | А |
| (xn)" | грях х | н |
| ° С" | u"v + uv" | ДА СЕ |
| (Cu)" | 1/cos 2x | T |
| (грех х)" | (u "v - u v") / v 2 | СЪС |
| (cos x)" | 0 | ОТНОСНО |
| (tg x)" | u"+v" | д |
| (ctg x)" | C u" | н |
| д | u"+v" | (u +v)" |
| ДА СЕ | u"v + uv" | (u v)" |
| СЪС | (u "v - u v") / v 2 | (u/v)" |
| П | n x n-1 | (xn)" |
| ОТНОСНО | 0 | ° С" |
| н | C u" | (Cu)" |
| д | Cos x | (грех х)" |
| н | -Грях х | (cos x)" |
| T | 1/cos 2x | (tg x)" |
| А | -1/sin2x | (ctg x)" |
Проверете отговора си спрямо таблицата: ( слайд 10)
II.Изучаване на нова тема:
1) Изследователска работа с използване на ESM ресурси на лаптопи. Работете по двойки.
Открийте Digital в Интернет образователни ресурсипо алгебра и принципи на анализа, тема за 11 клас: „Производни на експоненциалната функция, числото e и натурален логаритъм.“ модул I1
Прочетете внимателно всеки елемент от модула, запишете основните формули в тетрадките си и прочетете техните доказателства.
Изпълнете задачи за самоконтрол. Проверете резултатите от работата си в „Статистика“ (C).
Работен план на модула:
Експоненциална функция с основа е. – (Въведение в степента)
Формула за производната на експоненциална функция. – (Извеждане на формулата за производната на функцията y = e x)
Задача за самоконтрол. – (тест с избираем отговор)
Дефиниция на натурален логаритъм ln. – (ln x = log e x)
Формула за производната на експоненциална функция. – (извеждане на формулата на производната експоненциална формула)
Задача за самоконтрол. – (Задача с кратък отговор)
Първоизводна на експоненциалната функция – (извеждане на формулата за производната на експоненциалната функция)
Задача за самоконтрол – (тест с множество отговори)
2)
° Сл. 15-18Фронтално проучване въз основа на изучения материал. Първично консолидиране на материала. Приложение на формули за производна на показателна функция.
(д х )" = д х ;
(д х + b )" = кд kx + b ;
(а х )" = а х ∙ вътреа ;
(а kx + b )" = kа Kx +b ∙ вътреа
F(a х ) =
Ученикът работи самостоятелно на дъската:
Решение: f(x) = x 2 * 2 –x; D(f) = R; f " = 2x * 2 –x – x 2 * 2 -x ln2, D(f) =R,
2x * 2 –x – x 2 * 2 –x ln2 = 0;
X * 2 -x (2 – x * ln 2) = 0; - min + max - f " (x)
X * 2 –x = 0; 2 – x * ln x = 0 2 – x > 0, x = 0; 2 – x * ln2 = 0 0 2/ln2 f(x)
Отговор: x max = 2 / ln2; x min = 0
Самостоятелна работаобразователен характер:
Самостоятелна работа по двойки на лаптопи. Интерактивен модул P1 „Производна на експоненциална функция. Число e. Натурален логаритъм." – тест от 5 задачи. Когато отворите модул, на всеки компютър се извеждат различни задачи.
V. Обобщение на урока: Какво ново научихте в урока?
Кои моменти от урока бяха най-интересни за вас?
Кой е доволен от работата си в клас?
VI. Домашна работа: стр. 41; № 539(a,b,d); 540(c); 542(a,b); 544(b).
Интерактивен тест с компютър.Свойства на експоненциалната функция K1.
На работния плот на всеки компютър отворете Module Cl. единадесет
"Свойства на експоненциалната функция K1". Щракнете с мишката върху „play module“. Ще получите тест от 5 задачи.
Изпълнете задача 1 от модула, щракнете с мишката върху номера на верния отговор или запишете отговора в теста. Кликнете върху „отговор“ с мишката и преминете към друга задача.
Ако сте изпълнили задачата неправилно, отворете подсказката,
намерете грешката във вашето решение.
Проверете резултатите от работата си в „Статистика“ (C).
Производната на степен е равна на самата степен (производната на e на степен x е равна на e на степен x):
(1)
(e x )′ = e x.
Производната на експоненциална функция с основа a е равна на самата функция, умножена по натурален логаритъм от a:
(2)
.
Извеждане на формулата за производната на експоненциала, e на степен x
Експоненциалът е експоненциална функция, чиято основа е равна на числото e, което е следната граница:
.
Тук може да бъде или естествено число, или реално число. След това извеждаме формула (1) за производната на експонентата.
Извеждане на формулата за експоненциална производна
Помислете за експоненциала, e на степен x:
y = e x.
Тази функция е дефинирана за всички. Нека намерим неговата производна по отношение на променливата x. По дефиниция производната е следната граница:
(3)
.
Нека трансформираме този израз, за да го редуцираме до известни математически свойства и правила. За целта се нуждаем от следните факти:
а)Експонентно свойство:
(4)
;
б)Свойство на логаритъма:
(5)
;
IN)Непрекъснатост на логаритъма и свойството на границите за непрекъсната функция:
(6)
.
Ето една функция, която има граница и тази граница е положителна.
G)Значението на втората забележителна граница:
(7)
.
Нека приложим тези факти към нашия лимит (3). Използваме свойство (4):
;
.
Да направим замяна. Тогава ; .
Поради непрекъснатостта на експоненциала,
.
Следователно, когато , . В резултат получаваме:
.
Да направим замяна. Тогава . В , . И ние имаме:
.
Нека приложим свойството логаритъм (5):
. Тогава
.
Нека приложим свойство (6). Тъй като има положителна граница и логаритъма е непрекъснат, тогава:
.
Тук също използвахме втората забележителна граница (7). Тогава
.
Така получихме формула (1) за производната на експонентата.
Извеждане на формулата за производна на експоненциална функция
Сега извеждаме формула (2) за производната на експоненциалната функция с основа от степен a. Ние вярваме, че и. След това експоненциалната функция
(8)
Определено за всеки.
Нека трансформираме формула (8). За да направим това, ще използваме свойствата на експоненциалната функция и логаритъма.
;
.
И така, трансформирахме формула (8) в следния вид:
.
Производни от по-висок порядък на e на степен x
Сега нека намерим производни от по-високи разряди. Нека първо да разгледаме експонентата:
(14)
.
(1)
.
Виждаме, че производната на функция (14) е равна на самата функция (14). Диференцирайки (1), получаваме производни от втори и трети ред:
;
.
Това показва, че производната от n-ти ред също е равна на оригиналната функция:
.
Производни от по-висок порядък на експоненциалната функция
Сега разгледайте експоненциална функция с основа степен a:
.
Открихме неговата производна от първи ред:
(15)
.
Диференцирайки (15), получаваме производни от втори и трети ред:
;
.
Виждаме, че всяко диференциране води до умножаване на оригиналната функция с . Следователно производната от n-ти ред има следната форма:
.
Когато извеждаме първата формула от таблицата, ще продължим от дефиницията на производната функция в точка. Да вземем къде х– всяко реално число, т.е. х– всяко число от областта на дефиниране на функцията. Нека запишем границата на съотношението на нарастването на функцията към увеличението на аргумента при: ![]()
Трябва да се отбележи, че под граничния знак се получава изразът, който не е несигурността на нула, разделена на нула, тъй като числителят не съдържа безкрайно малка стойност, а точно нула. С други думи, увеличението на константна функция винаги е нула.
По този начин, производна на постоянна функцияе равно на нула в цялата област на дефиниране.
Производна на степенна функция.
Формулата за производната на степенна функция има формата ![]() , където степента стр– всяко реално число.
, където степента стр– всяко реално число.
Нека първо докажем формулата за естествения показател, т.е p = 1, 2, 3, …
Ще използваме определението за производна. Нека запишем границата на съотношението на увеличението на степенна функция към увеличението на аргумента: 
За да опростим израза в числителя, се обръщаме към биномната формула на Нютон: 
следователно 
Това доказва формулата за производната на степенна функция за естествен показател.
Производна на експоненциална функция.
Представяме извеждането на формулата за производна въз основа на определението:
Стигнахме до несигурност. За да го разширим, въвеждаме нова променлива и в . Тогава . При последния преход използвахме формулата за преход към нова логаритмична основа.
Нека заместим в първоначалния лимит: 
Ако си припомним втората забележителна граница, стигаме до формулата за производната на експоненциалната функция: 
Производна на логаритмична функция.
Нека докажем формулата за производната на логаритмична функция за всички хот домейна на дефиницията и всички валидни стойности на основата алогаритъм По дефиниция на производна имаме: 
Както забелязахте, по време на доказателството трансформациите бяха извършени с помощта на свойствата на логаритъма. Равенство  е вярно поради втората забележителна граница.
е вярно поради втората забележителна граница.
Производни на тригонометрични функции.
За да изведем формули за производни на тригонометрични функции, ще трябва да си припомним някои тригонометрични формули, както и първото забележително ограничение.
По дефиниция на производната за функцията синус имаме ![]() .
.
Нека използваме формулата за разликата на синусите: 
Остава да се обърнем към първата забележителна граница: 
По този начин, производната на функцията грях хИма cos x.
Формулата за производната на косинуса се доказва по абсолютно същия начин. 
Следователно, производната на функцията cos xИма – грях х.
Ще изведем формули за таблицата с производни за тангенс и котангенс, използвайки доказани правила за диференциране (производна на дроб). 
Производни на хиперболични функции.
Правилата за диференциране и формулата за производната на експоненциалната функция от таблицата с производни ни позволяват да изведем формули за производните на хиперболичния синус, косинус, тангенс и котангенс. 
Производна на обратната функция.
За да избегнем объркване по време на представяне, нека обозначим с долен индекс аргумента на функцията, чрез която се извършва диференцирането, тоест това е производната на функцията f(x)от х.
Сега нека формулираме правило за намиране на производната на обратна функция.
Нека функциите y = f(x)И x = g(y)взаимно обратни, определени на интервалите и съответно. Ако в точка има крайна ненулева производна на функцията f(x), тогава в точката има крайна производна на обратната функция g(y), и ![]() . В друга публикация
. В друга публикация ![]() .
.
Това правило може да бъде преформулирано за всеки хот интервала , тогава получаваме  .
.
Нека проверим валидността на тези формули.
Нека намерим обратната функция за натурален логаритъм ![]() (Тук ге функция и х- аргумент). След като решихме това уравнение за х, получаваме (тук хе функция и г– нейният аргумент). Това е,
(Тук ге функция и х- аргумент). След като решихме това уравнение за х, получаваме (тук хе функция и г– нейният аргумент). Това е, ![]() и взаимно обратни функции.
и взаимно обратни функции.
От таблицата на производните виждаме това ![]() И
И ![]() .
.
Нека се уверим, че формулите за намиране на производните на обратната функция ни водят до същите резултати: 
Цели на урока:формира представа за числото д; доказване на диференцируемост на функция във всяка точка х;разгледайте доказателството на теоремата за диференцируемостта на функция; проверка на зрелостта на уменията и способностите при решаване на примери за тяхното приложение.
Цели на урока.
Образователни: повторете определението за производна, правила за диференциране, производна елементарни функции, припомнят си графиката и свойствата на показателната функция, развиват умението да намират производната на показателната функция и следят знанията с помощта на задача и тест за проверка.
Развитие: насърчаване на развитието на вниманието, развитието на логическото мислене, математическата интуиция, способността за анализ и прилагане на знания в нестандартни ситуации.
Образователни: култивиране на информационна култура, развиване на умения за работа в група и индивидуално.
Методи на обучение: словесно, визуално, активно.
Форми на обучение: колективно, индивидуално, групово.
Оборудване : учебник „Алгебра и началото на анализа“ (под редакцията на Колмогоров), всички задачи от група Б „Затворен сегмент“ под редакцията на A.L. Семенова, И. В. Ященко, мултимедиен проектор.
Стъпки на урока:
- Изявление на темата, целта и целите на урока (2 мин.).
- Подготовка за изучаване на нов материал чрез повтаряне на вече изучен материал (15 мин.).
- Въведение в новия материал (10 мин.)
- Първоначално разбиране и затвърждаване на нови знания (15 мин.).
- Домашна работа (1 мин.).
- Обобщаване (2 мин.).
По време на часовете
1. Организационен момент.
Обявена е темата на урока: „Производна на показателна функция. Номер д.”, цели, задачи. Слайд 1. Презентация
2. Активиране на опорни знания.
За целта на първия етап от урока ще отговаряме на въпроси и ще решаваме задачи за повторение. Слайд 2.
На дъската двама ученици работят върху карти, изпълнявайки задачи като Единен държавен изпит B8.
Задача за първи ученик:
Задача за втори ученик:

Останалите ученици работят самостоятелно по следните варианти:
| Опция 1 | Вариант 2 | ||
| 1. |  |
1. |  |
| 2. |  |
2. |  |
| 3. |  |
3. |  |
| 4. |  |
4. |  |
| 5. |  |
5. |  |
Двойките обменят решения и проверяват взаимно работата си, като проверяват отговорите на слайд 3.
Разглеждат се решенията и отговорите на учениците, работещи на дъската.
Преглед домашна работа№ 1904. Показан е слайд 4.
3. Актуализиране на темата на урока, създаване на проблемна ситуация.
Учителят иска да дефинира експоненциална функция и да изброи свойствата на функцията y = 2 x. Графиките на експоненциалните функции се изобразяват като гладки линии, към които във всяка точка може да се направи допирателна. Но съществуването на допирателна към графиката на функция в точка с абсцисата x 0 е еквивалентно на нейната диференцируемост при x 0.
За графиките на функцията y = 2 x и y = 3 x начертаваме допирателни към тях в точката с абциса 0. Ъглите на наклон на тези допирателни спрямо абцисната ос са приблизително равни съответно на 35° и 48° . Слайд 5.
Заключение: ако основата на експоненциалната функция Анараства от 2 до, например, 10, тогава ъгълът между допирателната към графиката на функцията в точката x = 0 и оста x постепенно се увеличава от 35° до 66,5°. Логично е да се предположи, че има защо А, за който съответният ъгъл е 45
Доказано е, че има число по-голямо от 2 и по-малко от 3. Обикновено се означава с буквата д. В математиката е установено, че числото д– ирационален, т.е. представлява безкрайна десетична непериодична дроб.
e = 2,7182818284590…
Забележка (не много сериозно). Слайд 6.
На следващия слайд 7 се появяват портрети на велики математици - Джон Напиер, Леонхард Ойлер и кратка информацияза тях.
- Разгледайте свойствата на функцията y=e x
- Доказателство на теорема 1. Слайд 8.
- Доказателство на теорема 2. Слайд 9.
4. Динамична пауза или релакс за очите.
(Начална позиция - седнало, всяко упражнение се повтаря 3-4 пъти):
1. Облегнете се назад, поемете дълбоко въздух, след това, навеждайки се напред, издишайте.
2. Облегнете се на стола, затворете клепачи, затворете плътно очи, без да отваряте клепачите си.
3. Ръцете покрай тялото, кръгови движения на раменете напред и назад.
5. Затвърдяване на изучения материал.
5.1 Решение на упражнения № 538, № 540, № 544в.
5.2 Самостоятелно прилагане на знания, умения и способности. Работа по проверкатапод формата на тест. Време за изпълнение на задачата – 5 минути.
Критерии за оценка:
„5“ – 3 точки
„4“ – 2 точки
"3" - 1 точка
6. Обобщаване на резултатите от работата в урока.
- Отражение.
- Класиране.
- Изпращане на тестови задачи.
7. Домашна работа: параграф 41 (1, 2); № 539 (а, б, г); 540 (c, d), 544 (a, b).
“Затворен сегмент” № 1950, 2142.