Цифров кръг с пи числа. Тригонометричен кръг

Координати хточки, лежащи върху окръжността, са равни на cos(θ), а координатите гсъответстват на sin(θ), където θ е големината на ъгъла.

• Ако ви е трудно да си спомните това правило, просто помнете, че в двойката (cos; sin) „синусът е последен“.
• Това правило може да се изведе чрез разглеждане правоъгълни триъгълниции дефиниране на данни тригонометрични функции(синусът на ъгъла е равен на отношението на дължината на срещуположната страна, а косинусът е равен на отношението на съседната страна към хипотенузата).

Запишете координатите на четири точки от окръжността.„Единична окръжност“ е окръжност, чийто радиус е равен на единица. Използвайте това, за да определите координатите хИ гв четири точки на пресичане на координатните оси с окръжността. По-горе, за яснота, обозначихме тези точки като „изток“, „север“, „запад“ и „юг“, въпреки че нямат установени имена.

• "Изток" съответства на точката с координати (1; 0) .
• "Север" съответства на точката с координати (0; 1) .
• "Запад" отговаря на точката с координати (-1; 0) .
• "Юг" съответства на точката с координати (0; -1) .
• Това е подобно на обикновена графика, така че няма нужда да запомняте тези стойности, просто запомнете основния принцип.

Запомнете координатите на точките в първия квадрант.Първият квадрант се намира в горната дясна част на кръга, където са координатите хИ гприемам положителни стойности. Това са единствените координати, които трябва да запомните:

• точката π / 6 има координати () ;
• точката π/4 има координати () ;
• точката π / 3 има координати () ;
• Имайте предвид, че числителят приема само три стойности. Ако се движите в положителна посока (отляво надясно по оста хи отдолу нагоре по оста г), числителят приема стойностите 1 → √2 → √3.

Начертайте прави линии и определете координатите на точките на тяхното пресичане с кръга.Ако начертаете прави хоризонтални и вертикални линии от точките на един квадрант, вторите точки на пресичане на тези линии с окръжността ще имат координатите хИ гс еднакви абсолютни стойности, но различни знаци. С други думи, можете да начертаете хоризонтални и вертикални линии от точките на първия квадрант и да обозначите точките на пресичане с кръга със същите координати, но в същото време да оставите място отляво за правилния знак ("+" или "-").

• Например, можете да начертаете хоризонтална линия между точките π/3 и 2π/3. Тъй като първата точка има координати ( 1 2 , 3 2 (\displaystyle (\frac (1)(2)),(\frac (\sqrt (3))(2)))), координатите на втората точка ще бъдат (? 12 , ? 3 2 (\displaystyle (\frac (1)(2)),?(\frac (\sqrt (3))(2)))), където вместо знака "+" или "-" има въпросителен знак.
• Използвайте най-простия метод: обърнете внимание на знаменателите на координатите на точката в радиани. Всички точки със знаменател 3 имат еднакви абсолютни координатни стойности. Същото важи и за точки със знаменател 4 и 6.

За да определите знака на координатите, използвайте правилата за симетрия.Има няколко начина да определите къде да поставите знака "-":

• Запомнете основните правила за редовни графики. ос хотрицателна отляво и положителна отдясно. ос готрицателно отдолу и положително отгоре;
• започнете с първия квадрант и начертайте линии до други точки. Ако линията пресича оста г, координирайте хще смени знака си. Ако линията пресича оста х, знакът на координатата ще се промени г;
• запомнете, че в първия квадрант всички функции са положителни, във втория квадрант само синусът е положителен, в третия квадрант само тангенсът е положителен, а в четвъртия квадрант само косинусът е положителен;
• Който и метод да използвате, трябва да получите (+,+) в първия квадрант, (-,+) във втория, (-,-) в третия и (+,-) в четвъртия.

Проверете дали сте направили грешка.По-долу е пълен списъккоординати на „специални“ точки (с изключение на четири точки на координатните оси), ако се движите по единичния кръг обратно на часовниковата стрелка. Не забравяйте, че за да определите всички тези стойности, е достатъчно да запомните координатите на точките само в първия квадрант:

• първи квадрант: ( 3 2 , 1 2 (\displaystyle (\frac (\sqrt (3))(2)),(\frac (1)(2)))); (2 2 , 2 2 (\displaystyle (\frac (\sqrt (2))(2)),(\frac (\sqrt (2))(2)))); (1 2 , 3 2 (\displaystyle (\frac (1)(2)),(\frac (\sqrt (3))(2))));
• втори квадрант: ( − 1 2 , 3 2 (\displaystyle -(\frac (1)(2)),(\frac (\sqrt (3))(2)))); (− 2 2 , 2 2 (\displaystyle -(\frac (\sqrt (2))(2)),(\frac (\sqrt (2))(2)))); (− 3 2 , 1 2 (\displaystyle -(\frac (\sqrt (3))(2)),(\frac (1)(2))));
• трети квадрант: ( − 3 2 , − 1 2 (\displaystyle -(\frac (\sqrt (3))(2)),-(\frac (1)(2)))); (− 2 2 , − 2 2 (\displaystyle -(\frac (\sqrt (2))(2)),-(\frac (\sqrt (2))(2)))); (− 1 2 , − 3 2 (\displaystyle -(\frac (1)(2)),-(\frac (\sqrt (3))(2))));
• четвърти квадрант: ( 1 2 , − 3 2 (\displaystyle (\frac (1)(2)),-(\frac (\sqrt (3))(2)))); (2 2 , − 2 2 (\displaystyle (\frac (\sqrt (2))(2)),-(\frac (\sqrt (2))(2)))); (3 2 , − 1 2 (\displaystyle (\frac (\sqrt (3))(2)),-(\frac (1)(2)))).

Име на предмета Алгебра и началото на математическия анализ

Клас 10

UMK Алгебра и начало на математическия анализ, 10-11 клас. В 2 . Част 1. Учебник за образователни институции ( основно ниво на) /А.Г. Мордкович. – 10-то издание, ст. – М.: Мнемозина, 2012. Част 2. Проблемник за образователни институции (основно ниво) /[ А.Г. Мордкович и др.]; редактиран от А.Г. Мордкович. – 10-то издание, ст. – М.: Мнемозина, 2012.

Ниво на обучение. База

Тема на урока Цифров кръг (2 часа)

Урок 1

Мишена: въведе понятието числова окръжност като модел на криволинейна координатна система.

Задачи : да се развие способността да се използва числовият кръг при решаване на задачи.

Планирани резултати:

По време на часовете

Организиране на времето.

2. Проверка на домашните, които са затруднили учениците

II. Устна работа.

1. Свържете всеки интервал на числовата ос с неравенство и аналитичен запис за интервала. Въведете данните в таблицата.

А (–  ; –5] д (–5; 5)

б [–5; 5] д (–  ; –5)

IN [–5; +  ) И [–5; 5)

Ж (–5; 5] З (–5; +  )

1 –5 < х < 5 5 –5  х  5

2 х –5 6 х  –5

3 –5 < х  5 7 5  х < 5

4 х < –5 8 х > –5

А

1. За разлика от изследваната числова ос, числовата окръжност е по-сложен модел. Концепцията за дъга, която лежи в основата му, не е надеждно разработена в геометрията.

2 . Работа с учебника . Нека да разгледаме практически пример с. 23–24 учебник (писта за бягане на стадион). Можете да помолите учениците да дадат подобни примери (движение на сателит в орбита, въртене на зъбно колело и т.н.).

3. Обосноваваме удобството на използването на единичната окръжност като числова.

4. Работа с учебника. Нека разгледаме примери от стр. 25–31 учебник. Авторите подчертават, че за успешното овладяване на модела на числовата окръжност както в учебника, така и в учебника е предвидена система от специални „ дидактически игри" Има шест от тях, в този урок ще използваме първите четири.

(Мордкович А. Г. M79 Алгебра и началото на математическия анализ. 10-11 клас (основно ниво): Инструментариумза учителя / А. Г. Мордкович, П. В. Семенов. - М.: Мнемосина, 2010. - 202 с. : аз ще.)

1-ва "игра" – изчисляване на дължината на дъгата на единична окръжност. Учениците трябва да свикнат с факта, че дължината на целия кръг е 2 , половин кръг – , четвърт кръг –и т.н.

2-ра "игра" – намиране на точки от числовата окръжност, съответстващи на дадени числа, изразени в дроби от числото например точки и т.н. („добри“ числа и точки).

3-та "игра" – намиране на точки от числовата окръжност, които съответстват на дадени числа, неизразени в дроби от числото например точки М (1), М (–5) и т.н. („лоши“ числа и точки).

4-та "игра" – записване на числа, съответстващи на дадена „добра“ точка от числовата окръжност, например средата на първата четвърт е „добра“, числата, съответстващи на нея, имат формата

Динамична пауза

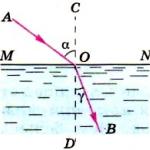
Упражненията, решени в този урок, съответстват на четирите посочени дидактически игри. Учениците използват оформление на числови кръгове с диаметриAC (хоризонтално) иBD(вертикално).

1. № 4.1, № 4.3.

Решение:

№ 4.3.

2. № 4.5 (а; б) – 4.11 (а; б).

3. № 4.12.

4. № 4.13 (а; б), № 4.14.

Решение:

№ 4.13.

V. Контролна работа.

Опция 1

Вариант 2

1. Отбележете точката върху числовия кръг, който съответства на това число:

2. Намерете всички числа, които отговарят на точките, отбелязани върху числовата окръжност.

VI. Обобщение на урока.

Въпроси към учениците:

– Дайте дефиницията на числова окръжност.

– Каква е дължината на единична окръжност? Дължина на половин единична окръжност? Нейната квартира?

– Как можете да намерите точка в числовата окръжност, която съответства на число?номер 5?

Домашна работа:, страница 23. No 4.2, No 4.4, No 4.5 (c; d) – No 4.11 (c; d), No 4.13 (c; d), No 4.15.

Урок №2

цели : консолидирайте концепцията за числовия кръг като модел на криволинейна координатна система.

Задачи : продължете да развивате способността да намирате точки в числовия кръг, които съответстват на дадени „добри“ и „лоши“ числа; запишете числото, съответстващо на точка от числовата окръжност; развиват способността да съставят аналитичен запис на дъгата на числова окръжност във формата двойно неравенство.

Развийте изчислителни умения, правилна математическа реч, логично мисленестуденти.

Възпитавайте независимост, внимание и точност. Възпитавайте отговорно отношение към ученето.

Планирани резултати:

Знайте, разбирайте: - числов кръг.

Да умее: - да намира точки върху окръжност по дадени координати; - намиране на координатите на точка, разположена върху числова окръжност.

Да може да прилага изучения теоретичен материал при изпълнение на писмена работа.

Техническа поддръжка на урока Компютър, екран, проектор, учебник, проблемник.

Допълнителна методическа и дидактическа подкрепа на урока: Мордкович А. Г. M79 Алгебра и началото на математическия анализ. 10-11 клас (основно ниво): методическо ръководство за учители / А. Г. Мордкович, П. В. Семенов. - М.: Мнемосина, 2010. - 202 с. : тиня

По време на часовете

Организиране на времето.

Психологическото настроение на учениците.

Проверка на домашните№ 4.2, № 4.4, № 4.5 (c; d) – № 4.11 (c; d), № 4.13 (c; d),

№ 4.15. Анализирайте решението на задачи, които са причинили затруднения.

Устна работа.

(на слайд)

1. Свържете точките от числовата окръжност и дадените числа:

а)

б)

V)

G)

д)

д)

и)

з)

2. Намерете точките върху числовата окръжност.

–2; 4; –8; 13.

III. Обяснение на нов материал.

Както вече беше отбелязано, учениците овладяват система от шест дидактически „игри“, които дават възможност за решаване на задачи от четири основни типа, свързани с числовата окръжност (от число до точка; от точка до число; от дъга до двойно неравенство; от двойно неравенство към дъга).

(Мордкович А. Г. M79 Алгебра и началото на математическия анализ. 10-11 клас (основно ниво): методическо ръководство за учители / А. Г. Мордкович, П. В. Семенов. - М.: Мнемозина, 2010. - 202 с. : аз ще.)

В този урок ще използваме последните две игри:

5-та "игра" – съставяне на аналитични записи (двойни неравенства) за дъги от числовата окръжност. Например, ако е дадена дъга, свързваща средата на първата четвърт (началото на дъгата) и най-ниската точка от двете, които разделят втората четвърт на три равни части (края на дъгата), тогава съответната аналитична нотацията има формата:

Ако началото и краят на една и съща дъга се разменят, тогава съответният аналитичен запис на дъгата ще изглежда така:

Авторите на учебника отбелязват, че термините „ядро на аналитичното записване на дъга“, „аналитично записване на дъга“ не са общоприети, те са въведени по чисто методически причини и дали да се използват или не, зависи от учител.

6-та "игра" – от този аналитичен запис на дъгата (двойно неравенство) преминете към нейния геометричен образ.

Обяснението трябва да се извърши с помощта на техниката на аналогията. Можете да използвате модел на подвижен числов ред, който може да бъде „свит“ в числов кръг.

Работа с учебника .

Нека разгледаме пример 8 от стр. 33 учебник.

Динамична пауза

IV. Формиране на умения и способности.

Когато изпълняват задачите, учениците трябва да се уверят, че когато пишат дъга аналитично, лявата страна на двойното неравенство е по-малка от дясната страна. За да направите това, когато записвате, трябва да се движите в положителна посока, т.е. обратно на часовниковата стрелка.

1-ва група . Упражнения за намиране на „лоши“ точки в числовата окръжност.

№ 4.16, № 4.17 (a; b).

2-ра група . Упражнения за аналитичен запис на дъга и изграждане на дъга въз основа на нейния аналитичен запис.

№ 4.18 (а; б), № 4.19 (а; б), № 4.20 (а; б).

V. Самостоятелна работа.

опция 1

3. Според аналитичния модел запишете обозначението на цифровата дъга и изградете нейния геометричен модел.

опция 2

1. Въз основа на геометричния модел на дъгата на числовата окръжност напишете аналитичния модел под формата на двойно неравенство.

2. По даденото обозначение на дъгата на числовата окръжност посочете неговите геометрични и аналитични модели.

3. Според аналитичния модел запишете обозначението на дъгата на числовата окръжност и изградете нейния геометричен модел.

VI. Обобщение на урока.

Въпроси към учениците:

– По какви начини можете да напишете аналитично дъгата на числовата окръжност?

– Какво се нарича сърцевина на аналитичния запис на дъга?

– На какви условия трябва да отговарят числата отляво и отдясно на двойно неравенство?

Домашна работа:

1. , страница 23. No 4.17 (c; d), No 4.18 (c; d), No 4.19 (c; d), No 4.20 (c; d).

2. Въз основа на геометричния модел на дъгата на числовата окръжност запишете нейния аналитичен модел под формата на двойно неравенство.

3. По даденото обозначение на дъгата на числовата окръжност посочете неговите геометрични и аналитични модели.

Ако вече сте запознати с тригонометричен кръг , и просто искате да опресните паметта си за определени елементи или сте напълно нетърпеливи, тогава ето го:

Тук ще анализираме всичко подробно стъпка по стъпка.

Тригонометричният кръг не е лукс, а необходимост

Тригонометрия Много хора го свързват с непроходими гъсталаци. Изведнъж се натрупват толкова много стойности на тригонометрични функции, толкова много формули... Но все едно не се получи в началото и... тръгваме... пълно недоразумение...

Много е важно да не се отказвате стойности на тригонометрични функции, - казват те, винаги можете да погледнете шпора с таблица със стойности.

Ако постоянно гледате таблица със стойности тригонометрични формули, нека се отървем от този навик!

Той ще ни помогне! Ще работите с него няколко пъти и след това ще изскочи в главата ви. Какво е той по-добри маси? Да, в таблицата ще намерите ограничен брой стойности, но в кръга - ВСИЧКО!

Например, кажете, докато гледате стандартна таблица със стойности на тригонометрични формули , колко е синусът, равен на, да кажем, 300 градуса или -45.

Няма начин?.. можете, разбира се, да се свържете формули за намаляване... И като погледнете тригонометричната окръжност, можете лесно да отговорите на такива въпроси. И скоро ще разберете как!

И когато решавате тригонометрични уравненияа неравенства без тригонометричната окръжност - никъде.

Въведение в тригонометричния кръг

Да вървим по ред.

Първо, нека напишем тази поредица от числа:

А сега това:

И накрая този:

Разбира се, ясно е, че всъщност на първо място е , на второ място е , а на последно място е . Тоест повече ще ни интересува веригата.

Но колко красиво се оказа! Ако нещо се случи, ние ще възстановим тази „стълба-чудо“.

И защо ни трябва?

Тази верига е основните стойности на синус и косинус през първото тримесечие.

Нека начертаем окръжност с единичен радиус в правоъгълна координатна система (тоест вземаме всеки радиус по дължина и обявяваме дължината му за единица).

От гредата „0-Start“ поставяме ъглите по посока на стрелката (виж фигурата).

Получаваме съответните точки на окръжността. Така че, ако проектираме точките върху всяка от осите, тогава ще получим точно стойностите от горната верига.

Защо е това, ще попитате?

Нека не анализираме всичко. Нека помислим принцип, което ще ви позволи да се справите с други подобни ситуации.

Триъгълник AOB е правоъгълен и съдържа . И знаем, че срещу ъгъл b лежи катет с половината от размера на хипотенузата (имаме хипотенузата = радиуса на окръжността, тоест 1).

Това означава AB= (и следователно OM=). И според Питагоровата теорема

Надявам се вече нещо да се изясни?

Така че точка B ще съответства на стойността, а точка M ще съответства на стойността

Същото и с другите стойности от първото тримесечие.

Както разбирате, познатата ос (вол) ще бъде косинусова ос, а оста (oy) – ос на синусите . По късно.

Вляво от нулата по косинусовата ос (под нулата по синусовата ос) ще има, разбира се, отрицателни стойности.

И така, ето го ВСЕМОГЪЩИЯТ, без когото няма никъде в тригонометрията.

Но ние ще говорим за това как да използваме тригонометричния кръг в.

>> Цифров кръг

Докато изучавахме курса по алгебра за 7-9 клас, досега се занимавахме с алгебрични функции, т.е. функции, дефинирани аналитично чрез изрази, в които са използвани алгебрични операции върху числа и променливи (събиране, изваждане, умножение, разделение, степенуване, извличане корен квадратен). Но математическите модели на реални ситуации често се свързват с функции от различен тип, а не алгебрични. С първите представители на класа неалгебрични функции – тригонометричните функции – ще се запознаем в тази глава. Ще изучавате тригонометрични функции и други видове неалгебрични функции (експоненциални и логаритмични) по-подробно в гимназията.
За да въведем тригонометрични функции, се нуждаем от нов математически модел- кръг с числа, който все още не сте срещали, но сте много запознати с числовата линия. Спомнете си, че числовата линия е права линия, на която са дадени началната точка O, мащабът (единичната отсечка) и положителната посока. Можем да сравним всяко реално число с точка на права и обратно.

Как да намерим съответната точка M на права с помощта на числото x? Числото 0 съответства на началната точка O. Ако x > 0, тогава, движейки се по права линия от точка 0 в положителна посока, трябва да преминете n^th с дължина x; краят на този път ще бъде желаната точка M(x). Ако x< 0, то, двигаясь по прямой из точки О в отрицательном направлении, нужно пройти путь 1*1; конец этого пути и будет искомой точкой М(х). Число х - координата точки М.

Как решихме обратна задача, т.е. Как намерихте координатата x на дадена точка M на числовата ос? Намерихме дължината на сегмента OM и го взехме със знака „+“ или * - „в зависимост от това от коя страна на точката O се намира точката M на правата линия.

Но в Истински животТрябва да се движите не само по права линия. Доста често движение по кръг. Ето един конкретен пример. Нека приемем, че пистата за бягане на стадиона е кръг (всъщност това, разбира се, не е кръг, но не забравяйте, както обикновено казват спортните коментатори: „бегачът е пробягал кръг“, „остава половин кръг“ да бягаш преди финала” и др.), дължината му е 400 м. Стартът е маркиран - точка А (фиг. 97). Бегачът от точка А се движи около кръга обратно на часовниковата стрелка. Къде ще бъде след 200 м? на 400 м? на 800 м? на 1500 м? Къде трябва да начертае финалната линия, ако бяга маратонска дистанция от 42 км 195 м?

След 200 m той ще бъде в точка C, диаметрално противоположна на точка A (200 m е дължината на половината бягаща пътека, т.е. дължината на половин кръг). След като избяга 400 м (т.е. „една обиколка“, както казват спортистите), той ще се върне в точка А. След като избяга 800 м (т.е. „две обиколки“), той отново ще бъде в точка А. Какво е 1500 м ? Това са “три кръга” (1200 м) плюс още 300 м, т.е. 3

Бягаща пътека - финалът на тази дистанция ще бъде в точка 2) (фиг. 97).

Просто трябва да се справим с маратона. След като пробяга 105 обиколки, спортистът ще измине разстояние от 105-400 = 42 000 м, т.е. 42 км. До финала остават 195 м, което е с 5 м по-малко от половината обиколка. Това означава, че финалът на маратонското разстояние ще бъде в точка М, разположена близо до точка С (фиг. 97).

Коментирайте. Вие, разбира се, разбирате конвенцията на последния пример. Никой не бяга маратонско разстояние около стадиона, максимумът е 10 000 м, т.е. 25 обиколки.

Можете да бягате или да ходите на произволна дължина по бягащата пътека на стадиона. Това означава, че всяко положително число съответства на някаква точка - „финала на разстоянието“. Освен това всеки може отрицателно числосъпоставете точка от кръга: просто трябва да накарате спортиста да тича в обратната посока, т.е. започнете от точка А не обратно на часовниковата стрелка, а по посока на часовниковата стрелка. Тогава пистата на стадиона може да се разглежда като числов кръг.

По принцип всяка окръжност може да се разглежда като числова окръжност, но в математиката е прието за тази цел да се използва единична окръжност - окръжност с радиус 1. Това ще бъде нашата „бягаща пътека“. Дължината b на окръжност с радиус K се изчислява по формулата Дължината на половин окръжност е n, а дължината на четвърт окръжност е AB, BC, SB, DA на фиг. 98 - равен Нека се съгласим да наричаме дъга AB първата четвърт от единичната окръжност, дъга BC втората четвърт, дъга CB третата четвърт, дъга DA четвъртата четвърт (фиг. 98). В същото време обикновено ние говорим заотносно Open Arc, т.е. за дъга без краищата (нещо като интервал на числова ос).

Определение.Дадена е единична окръжност, върху която е отбелязана началната точка А - десният край на хоризонталния диаметър (фиг. 98). Нека свържем всяко реално число I с точка от окръжността съгласно следното правило:

1) ако x > 0, тогава, движейки се от точка А в посока, обратна на часовниковата стрелка (положителната посока на обикаляне по окръжността), ще опишем път по окръжността с дължина и крайната точка М на този път ще бъде желаната точка: M = M(x);

2) ако x< 0, то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь длиной и |; конечная точка М этого пути и будет искомой точкой: М = М(1);

Нека свържем точка A с 0: A = A(0).

Единична окръжност с установено съответствие (между реални числа и точки от окръжността) ще наричаме числова окръжност.
Пример 1.Намерете в числовия кръг
Тъй като първите шест от дадените седем числа са положителни, тогава за да намерите съответните точки на окръжността, трябва да изминете път с дадена дължина по окръжността, движейки се от точка А в положителна посока. Нека вземем предвид това

Числото 2 съответства на точка А, тъй като преминавайки по окръжността път с дължина 2, т.е. точно една окръжност, ние отново ще стигнем до началната точка A И така, A = A(2).
Какво стана Това означава, че движейки се от точка А в положителна посока, трябва да преминете през цял кръг.

Коментирайте.Когато сме в 7 и 8 клас работешес числовата ос, тогава се съгласихме, за краткост, да не казваме „точката на правата, съответстваща на числото x“, а да кажем „точка x“. Ние ще се придържаме към абсолютно същото споразумение, когато работим с числовия кръг: „точка f“ - това означава, че говорим за точка от кръга, която съответства на числото
Пример 2.
Разделяйки първата четвърт AB на три равни части с точки K и P, получаваме:

Пример 3.Намерете точки в числовия кръг, които съответстват на числа
Ще направим конструкции с помощта на фиг. 99. Отлагайки дъга AM (дължината й е -) от точка А пет пъти в отрицателна посока, получаваме точка!, - средата на дъга BC. Така,

Коментирайте.Обърнете внимание на някои от свободите, които приемаме при използването на математическия език. Ясно е, че дъгата AK и дължината на дъгата AK са различни неща (първата концепция е геометрична фигура, а второто понятие е число). Но и двете са обозначени по един и същи начин: AK. Освен това, ако точките A и K са свързани с сегмент, тогава и полученият сегмент, и неговата дължина се означават по същия начин: AK. Обикновено от контекста става ясно какво значение има в обозначението (дъга, дължина на дъгата, сегмент или дължина на сегмента).

Следователно оформлението на кръг с две числа ще ни бъде много полезно.

ПЪРВО ОФОРМЛЕНИЕ
Всяка от четирите четвъртинки на числовия кръг е разделена на две равни части, а до всяка от наличните осем точки са изписани техните „имена“ (фиг. 100).

ВТОРО ОФОРМЛЕНИЕВсяка от четирите четвъртинки на числовия кръг е разделена на три равни части, а близо до всяка от наличните дванадесет точки са изписани техните „имена“ (фиг. 101).

Моля, обърнете внимание, че и на двете оформления можем да присвоим други „имена“ на дадените точки.
Забелязали ли сте, че във всички анализирани примери за дължини на дъги
изразено с някои дроби от числото n? Това не е изненадващо: в крайна сметка дължината на единична окръжност е 2n и ако разделим окръжност или нейната четвърт на равни части, получаваме дъги, чиито дължини са изразени в части от числото и. Мислите ли, че е възможно да се намери точка E върху единичната окръжност, така че дължината на дъгата AE да е равна на 1? Нека да го разберем:

Разсъждавайки по подобен начин, заключаваме, че върху единичната окръжност може да се намери точка Eg, за която AE = 1, и точка E2, за която AEr = 2, и точка E3, за която AE3 ​​= 3, и точка E4, за която AE4 = 4, и точка Eb, за която AEb = 5, и точка E6, за която AE6 = 6. На фиг. 102 са отбелязани (приблизително) съответните точки (за ориентация всяка от четвъртините на единичния кръг е разделена с чертички на три равни части).

Пример 4.Намерете точката в числовия кръг, съответстваща на числото -7.

Трябва, като започнем от точка A(0) и се движим в отрицателна посока (по часовниковата стрелка), да преминем по окръжност с дължина 7. Ако преминем през една окръжност, получаваме (приблизително) 6,28, което означава, че все още трябва да преминете през (в същата посока) път с дължина 0,72. Какъв вид дъга е това? Малко по-малко от половин четвърт кръг, т.е. дължината му е по-малка от числото -.

И така, на числова окръжност, подобно на числова ос, всяко реално число съответства на една точка (само, разбира се, по-лесно е да го намерите на права, отколкото на окръжност). Но за права линия обратното също е вярно: всяка точка съответства единствено число. За числова окръжност такова твърдение не е вярно; многократно сме виждали това по-горе. Следното твърдение е вярно за числовата окръжност.
Ако точка M от числовата окръжност съответства на числото I, то тя също съответства на число от вида I + 2k, където k е всяко цяло число (k e 2).

Всъщност 2n е дължината на числовата (единична) окръжност, а цялото число |th| може да се разглежда като броят на пълните обиколки на кръга в една или друга посока. Ако например k = 3, това означава, че правим три обиколки на кръга в положителна посока; ако k = -7, това означава, че правим седем (| k | = | -71 = 7) обиколки на кръга в отрицателна посока. Но ако сме в точка M(1), тогава, след като също извършихме | към | пълни кръгове около кръга, отново ще се окажем в точка M.

А.Г. Мордкович алгебра 10 клас

Съдържание на урока бележки към уроцитеподдържаща рамка презентация урок методи ускорение интерактивни технологии Практикувайте задачи и упражнения самопроверка работилници, обучения, казуси, куестове домашна работа въпроси за дискусия риторични въпроси от ученици Илюстрации аудио, видео клипове и мултимедияснимки, картинки, графики, таблици, диаграми, хумор, анекдоти, вицове, комикси, притчи, поговорки, кръстословици, цитати Добавки резюметастатии трикове за любознателните ясли учебници основен и допълнителен речник на термините други Подобряване на учебниците и уроцитекоригиране на грешки в учебникаактуализиране на фрагмент в учебник, елементи на иновация в урока, замяна на остарели знания с нови Само за учители перфектни уроци календарен планза година насокидискусионни програми Интегрирани уроци

Когато изучава тригонометрия в училище, всеки ученик се сблъсква с много интересна концепция"цифров кръг" От умение учител в училищеОбяснението какво е това и защо е необходимо зависи от това колко добре ученикът ще направи тригонометрията по-късно. За съжаление, не всеки учител може да обясни този материал ясно. В резултат на това много ученици са объркани дори как да отбелязват точки върху числовата окръжност. Ако прочетете тази статия до края, ще научите как да направите това без никакви проблеми.

Така че да започваме. Нека начертаем окръжност, чийто радиус е 1. Нека означим "най-дясната" точка на тази окръжност с буквата О:

Поздравления, току-що начертахте единична окръжност. Тъй като радиусът на тази окръжност е 1, нейната дължина е .

Всяко реално число може да се свърже с дължината на траекторията по числовата окръжност от точката О. Посоката на движение обратно на часовниковата стрелка се приема за положителна посока. За минус – по часовниковата стрелка:

Разположение на точките върху числовата окръжност

Както вече отбелязахме, дължината на числовата окръжност (единична окръжност) е равна на . Къде тогава ще се намира числото на този кръг? Очевидно, от точката Ообратно на часовниковата стрелка трябва да преминем половината от дължината на кръга и ще се окажем в желаната точка. Нека го обозначим с буквата б:

Обърнете внимание, че същата точка може да бъде достигната, като се движите в полукръг в отрицателна посока. След това ще начертаем числото върху единичната окръжност. Тоест числата съответстват на една и съща точка.

Освен това същата тази точка съответства и на числата , , , и като цяло на безкраен набор от числа, които могат да бъдат записани във формата , където , т.е. принадлежи на множеството от цели числа. Всичко това, защото от точката бможете да направите „околосветско“ пътуване във всяка посока (добавете или извадете обиколката) и стигнете до същата точка. Получаваме важен извод, който трябва да бъде разбран и запомнен.

Всяко число съответства на една точка от числовата окръжност. Но всяка точка от числовата окръжност съответства на безкраен брой числа.

Нека сега разделим горния полукръг на числовата окръжност на дъги еднаква дължинаточка ° С. Лесно се вижда, че дължината на дъгата O.C.равна на . Нека сега да се отложим от точката ° Сдъга със същата дължина в посока, обратна на часовниковата стрелка. В резултат на това ще стигнем до точката б. Резултатът е съвсем очакван, тъй като. Нека положим тази дъга отново в същата посока, но сега от точката б. В резултат на това ще стигнем до точката д, което вече ще съответства на числото:

Забележете отново, че тази точка съответства не само на числото, но също така, например, на числото, тъй като тази точка може да бъде достигната, като се отдалечите от точката Очетвърт кръг по посока на часовниковата стрелка (отрицателна посока).

И като цяло отново отбелязваме, че тази точка съответства на безкрайно много числа, които могат да бъдат записани във формата . Но те могат да бъдат записани и във формата . Или, ако предпочитате, под формата на. Всички тези записи са абсолютно еквивалентни и могат да бъдат получени един от друг.

Нека сега разделим дъгата на O.C.половин точка М. Сега разберете каква е дължината на дъгата ОМ? Точно така, половината дъга O.C.. Това е . На кои числа отговаря точката? Мвърху числовия кръг? Сигурен съм, че сега ще разберете, че тези числа могат да бъдат записани като .

Но може и по различен начин. Да вземем. Тогава разбираме това . Тоест, тези числа могат да бъдат записани във формата . Същият резултат може да се получи с помощта на числовия кръг. Както вече казах, двата записа са еквивалентни и могат да бъдат получени един от друг.

Сега лесно можете да дадете пример за числата, на които отговарят точките н, ПИ Квърху числовия кръг. Например числата и:

Често това е минимумът положителни числаи се приемат за обозначаване на съответните точки върху числовата окръжност. Въпреки че това изобщо не е необходимо, точка н, както вече знаете, съответства на безкраен брой други числа. Включително, например, числото.

Ако счупите дъгата O.C.на три равни дъги с точки СИ Л, така че това е смисълът Сще лежи между точките ОИ Л, след това дължината на дъгата операционна системаще бъде равна на , и дължината на дъгата OLще бъде равно на . Използвайки знанията, които придобихте в предишната част на урока, можете лесно да разберете как са се оказали останалите точки в числовата окръжност:

Числа, които не са кратни на π в числовата окръжност

Нека сега си зададем въпроса: къде на числовата ос трябва да отбележим точката, съответстваща на числото 1? За да направите това, трябва да започнете от най-„дясната“ точка на единичния кръг Оначертайте дъга, чиято дължина би била равна на 1. Можем само приблизително да посочим местоположението на желаната точка. Да процедираме по следния начин.