Определение. Ако функцията f(х) е дефинирана на интервала [ а, б], е непрекъсната във всяка точка от интервала ( а, б), в точка анепрекъснато вдясно, в точката bе непрекъсната отляво, тогава казваме, че функцията f(х) непрекъснат на сегмента [а, б].
С други думи, функцията f(х) е непрекъснат на интервала [ а, б], ако са изпълнени три условия:
1) "х 0 Î( а, б): f(х) = f(х 0);
2) f(х) = f(а);
3) f(х) = f(b).
За функции, които са непрекъснати на интервал, разглеждаме някои свойства, които формулираме под формата на следните теореми, без да провеждаме доказателства.
Теорема 1. Ако функцията f(х) е непрекъснат на интервала [ а, б], тогава той достига своите минимални и максимални стойности на този сегмент.
Тази теорема гласи (фиг. 1.15), че на сегмента [ а, б] има такава точка х 1 това f(х 1) £ f(х) за всякакви хот [ а, б] и че има смисъл х 2 (х 2 О[ а, б]) така че " хÎ[ а, б] (f(х 2)³ f(х)).
Значение f(х 1) е най-големият за дадена функция на [ а, б], А f(х 2) – най-малкият. Да обозначим: f(х 1) = М, f(х 2) =м. Тъй като за f(х) важи неравенството: " хÎ[ а, б] м£ f(х) £ М, тогава получаваме следното следствие от теорема 1.
Последица. Ако функцията f(х) е непрекъснат на интервал, тогава е ограничен на този интервал.
Теорема 2. Ако функцията f(х) е непрекъснат на интервала [ а,б] и в краищата на сегмента приема стойности на различни знаци, тогава има такава вътрешна точка х 0 сегмент [ а, б], при което функцията става 0, т.е. $ х 0 Î ( а, б) (f(х 0) = 0).
Тази теорема твърди, че графиката на функция y = f(х), непрекъснат на интервала [ а, б], пресича оста волпоне веднъж, ако стойностите f(а) И f(b) имат противоположни знаци. И така, (фиг. 1.16) f(а) > 0, f(b) < 0 и функция f(х) става 0 в точки х 1 , х 2 , х 3 .
Теорема 3. Нека функцията f(х) е непрекъснат на интервала [ а, б], f(а) = А, f(b) = бИ А¹ б. (фиг. 1.17). След това за произволен номер ° С, оградени между числата АИ б, има такава вътрешна точка х 0 сегмент [ а, б], Какво f(х 0) = ° С.
Последица. Ако функцията f(х) е непрекъснат на интервала [ а, б], м– най-малка стойност f(х), М – най-висока стойностфункции f(х) на сегмента [ а, б], тогава функцията приема (поне веднъж) произволна стойност м, сключен между мИ М, и следователно сегмента [ м, М] е множеството от всички стойности на функцията f(х) на сегмента [ а, б].
Обърнете внимание, че ако дадена функция е непрекъсната на интервала ( а, б) или има върху сегмента [ а, б] точки на прекъсване, тогава теореми 1, 2, 3 за такава функция престават да бъдат верни.
В заключение разгледайте теоремата за съществуването на обратна функция.
Нека припомним, че под интервал разбираме сегмент или интервал, или полуинтервал, краен или безкраен.
 |
Теорема 4. Позволявам f(х) е непрекъснат на интервала х, се увеличава (или намалява) с хи има диапазон от стойности Y. След това за функцията y = f(х) има обратна функция х= й(г), определен на интервала Y, непрекъснато и нарастващо (или намаляващо) с Yс множество значения х.
Коментирайте. Нека функцията х= й(г) е обратната на функцията f(х). Тъй като аргументът обикновено се означава с х, а функцията през г, тогава записваме обратната функция във формата y =й(х).
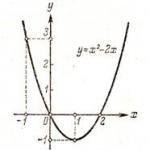
Пример 1. функция y = x 2 (фиг. 1.8, а) на комплекта х= ` и ``. Съгласно условието за екстремум, „x=-1“ е локална максимална точка, а „x=1“ е локална минимална точка. Тъй като `y^"=0` само в точките `x=1` и `x=-1`, то според теоремата на Ферма функцията няма други точки на екстремум.
Нека разгледаме важен клас проблеми, които използват концепцията за производна - проблемът за намиране на най-големите и най-малките стойности на функция в сегмент.
Пример 5.2
Намерете най-голямата и най-малката стойност на функцията `y=x^3-3x` върху отсечката: а) `[-2;0]`; б) ``.
а) От пример 5.1 следва, че функцията нараства с `(-oo,-1]` и намалява с `[-1,1]`. Така че `y(-1)>=y(x)` за всички ` x in[-2;0]` и `y_"max"=y(-1)=2` - най-голямата стойност на функцията в сегмента `[-2;0]`. За да намерите най-малката стойност, трябва да сравните стойностите на функцията в крайния сегмент. Тъй като `y(-2)=-2` и `y(0)=0`, тогава `y_"max"=-2` е най-малкото стойност на функцията върху сегмента `[-2;0]`.
б) Тъй като на лъча има ``, следователно `y_"naim"=y(1)=-2`, `y_"naib"=y(3)=18`.
Коментирайте
Имайте предвид, че функция, непрекъсната на интервал, винаги има най-голямата и най-малката стойност.
Пример 5.3
Намерете най-голямата и най-малката стойност на функцията `y=x^3-12|x+1|` върху сегмента `[-4;3]`.
Обърнете внимание, че функцията е непрекъсната на цялата числова ос. Нека означим `f_1(x)=x^3+12(x+1)`, `f_2(x)=x^3-12(x+1)`. След това `y=f_1(x)` при `-4<=x<=-1` и `y=f_2(x)` при `-1<=x<=3`. Находим `f_1^"(x)=3x^2+12`, `f_2^"(x)=3x^2-12`. Уравнение `f_1^"(x)=0` не имеет действительных корней, а уравнение `f_2^"(x)=0` имеет два действительных корня `x_1=-2`, `x_2=2`, из которых интервалу `(-1;3)` принадлежит только точка `x_2`. В точке `x=-1` функция определена, но не имеет производной (можно, например, провести рассуждения, аналогичные рассуждениям примера 4.2). Итак, имеется две критические точки: `x=-1` и `x=2`. Производная `y^"(x)=f_1^"(x)>0` до `(-4,-1)`, `y^"(x)=f_2^"(x)<0` на `(-1;2)` и `y^"(x)=f_2^"(x)>0` към `(2;3)`. Нека запишем всички изследвания в таблицата:
`y_"наиб"=-1`; `y_"име"=-100`.
От практическа гледна точка най-голям интерес представлява използването на производната за намиране на най-големите и най-малките стойности на функция. С какво е свързано това? Максимизиране на печалбите, минимизиране на разходите, определяне на оптималното натоварване на оборудването... С други думи, в много области на живота ни се налага да решаваме проблеми с оптимизирането на някои параметри. И това са задачите за намиране на най-големите и най-малките стойности на функция.
Трябва да се отбележи, че най-големите и най-малките стойности на функция обикновено се търсят на определен интервал X, който е или цялата област на функцията, или част от областта на дефиниция. Самият интервал X може да бъде сегмент, отворен интервал ![]() , безкраен интервал.
, безкраен интервал.
В тази статия ще говорим за намиране на най-голямата и най-малката стойност на изрично дефинирана функция на една променлива y=f(x).
Навигация в страницата.
Най-голяма и най-малка стойност на функция - определения, илюстрации.
Нека разгледаме накратко основните определения.
Най-голямата стойност на функцията ![]() че за всеки
че за всеки ![]() неравенството е вярно.
неравенството е вярно.
Най-малката стойност на функцията y=f(x) на интервала X се нарича такава стойност ![]() че за всеки
че за всеки ![]() неравенството е вярно.
неравенството е вярно.
Тези дефиниции са интуитивни: най-голямата (най-малката) стойност на функция е най-голямата (най-малката) приета стойност на разглеждания интервал на абсцисата.
Стационарни точки– това са стойностите на аргумента, при които производната на функцията става нула.
Защо се нуждаем от стационарни точки, когато намираме най-големите и най-малките стойности? Отговор на този въпрос дава теоремата на Ферма. От тази теорема следва, че ако диференцируема функция има екстремум (локален минимум или локален максимум) в дадена точка, тогава тази точка е неподвижна. По този начин функцията често приема своята най-голяма (най-малка) стойност на интервала X в една от стационарните точки от този интервал.
Също така, една функция често може да приеме своите най-големи и най-малки стойности в точки, в които първата производна на тази функция не съществува и самата функция е дефинирана.
Нека веднага да отговорим на един от най-често срещаните въпроси по тази тема: „Винаги ли е възможно да се определи най-голямата (най-малката) стойност на функция“? Не винаги. Понякога границите на интервала X съвпадат с границите на областта на дефиниране на функцията или интервалът X е безкраен. И някои функции в безкрайност и на границите на областта на дефиницията могат да приемат както безкрайно големи, така и безкрайно малки стойности. В тези случаи не може да се каже нищо за най-голямата и най-малката стойност на функцията.
За яснота ще дадем графична илюстрация. Вижте снимките и много неща ще ви станат по-ясни.
На сегмента

На първата фигура функцията приема най-големите (max y) и най-малките (min y) стойности в стационарни точки, разположени вътре в сегмента [-6;6].
Разгледайте случая, изобразен на втората фигура. Нека променим сегмента на . В този пример най-малката стойност на функцията се постига в стационарна точка, а най-голямата в точката с абсцисата, съответстваща на дясната граница на интервала.
На фигура 3 граничните точки на сегмента [-3;2] са абсцисите на точките, съответстващи на най-голямата и най-малката стойност на функцията.
На отворен интервал

На четвъртата фигура функцията приема най-големите (max y) и най-малките (min y) стойности в стационарни точки, разположени вътре в отворения интервал (-6;6).
На интервала не могат да се направят изводи за най-голямата стойност.
В безкрайност

В примера, представен на седмата фигура, функцията приема най-голямата стойност (max y) в стационарна точка с абциса x=1, а най-малката стойност (min y) се постига на дясната граница на интервала. При минус безкрайност стойностите на функцията асимптотично се доближават до y=3.
През интервала функцията не достига нито най-малката, нито най-голямата стойност. Когато x=2 се приближава отдясно, стойностите на функцията клонят към минус безкрайност (линията x=2 е вертикална асимптота), а когато абсцисата клони към плюс безкрайност, стойностите на функцията асимптотично се доближават до y=3. Графична илюстрация на този пример е показана на фигура 8.
Алгоритъм за намиране на най-големите и най-малките стойности на непрекъсната функция на сегмент.
Нека напишем алгоритъм, който ни позволява да намерим най-голямата и най-малката стойност на функция в сегмент.
- Намираме домейна на дефиниция на функцията и проверяваме дали съдържа целия сегмент.
- Намираме всички точки, в които първата производна не съществува и които се съдържат в отсечката (обикновено такива точки се намират във функции с аргумент под знака на модула и в степенни функции с дробно-рационален показател). Ако няма такива точки, преминете към следващата точка.
- Определяме всички неподвижни точки, попадащи в сегмента. За да направите това, ние го приравняваме към нула, решаваме полученото уравнение и избираме подходящи корени. Ако няма стационарни точки или нито една от тях не попада в сегмента, преминете към следващата точка.
- Изчисляваме стойностите на функцията в избрани стационарни точки (ако има такива), в точки, в които първата производна не съществува (ако има такава), както и при x=a и x=b.
- От получените стойности на функцията избираме най-голямата и най-малката - те ще бъдат съответно необходимите най-големи и най-малки стойности на функцията.
Нека анализираме алгоритъма за решаване на пример за намиране на най-големите и най-малките стойности на функция в сегмент.
Пример.
Намерете най-голямата и най-малката стойност на функция
- на сегмента;
- на отсечката [-4;-1] .
Решение.
Областта на дефиниране на функция е цялото множество от реални числа, с изключение на нулата, т.е. И двата сегмента попадат в областта на дефиницията.
Намерете производната на функцията по отношение на: 
Очевидно производната на функцията съществува във всички точки на отсечките и [-4;-1].
Определяме стационарни точки от уравнението. Единственият истински корен е x=2. Тази неподвижна точка попада в първия сегмент.
За първия случай изчисляваме стойностите на функцията в краищата на сегмента и в стационарната точка, т.е. за x=1, x=2 и x=4: 
Следователно най-голямата стойност на функцията ![]() се постига при x=1 и най-малката стойност
се постига при x=1 и най-малката стойност  – при х=2.
– при х=2.
За втория случай изчисляваме стойностите на функцията само в краищата на сегмента [-4;-1] (тъй като не съдържа нито една неподвижна точка): 
Решение.
Нека започнем с домейна на функцията. Квадратът на тричлена в знаменателя на дробта не трябва да се равнява на нула: 
Лесно се проверява дали всички интервали от формулировката на задачата принадлежат към областта на дефиниране на функцията.
Нека разграничим функцията: 
Очевидно производната съществува в цялата област на дефиниране на функцията.
Да намерим неподвижни точки. Производната отива на нула при . Тази неподвижна точка попада в интервалите (-3;1] и (-3;2).
Сега можете да сравните резултатите, получени във всяка точка, с графиката на функцията. Сините пунктирани линии показват асимптоти.

На този етап можем да завършим с намирането на най-голямата и най-малката стойност на функцията. Алгоритмите, разгледани в тази статия, ви позволяват да получите резултати с минимални действия. Въпреки това може да бъде полезно първо да се определят интервалите на нарастване и намаляване на функцията и едва след това да се правят заключения за най-големите и най-малките стойности на функцията на всеки интервал. Това дава по-ясна картина и строга обосновка на резултатите.
Непрекъснатост на функция върху отсечка.
Наред с непрекъснатостта на функцията в точка се разглежда и нейната непрекъснатост през различни интервали.
Функция f (x) се нарича непрекъсната в интервала (a, b), ако е непрекъсната във всяка точка от този интервал.
Казва се, че функция f (x) е непрекъсната в интервала [a, b], ако е непрекъсната в интервала (a, b), непрекъсната вдясно в точка a и непрекъсната вляво в точка b.
Функцията се извиква непрекъснат на сегмента, ако е непрекъснат в интервала, непрекъснато вдясно в точката, това е и непрекъснато отляво в точката, това е .
Коментирайте.Функция, която е непрекъсната на сегмента [a, b], може да бъде прекъсната в точки a и b (фиг. 1)

Множеството от функции, непрекъснати в интервала [a, b], се означава със символа C[a, b].
Основни теореми за непрекъснати на интервал функции.
Теорема 1(за ограничеността на непрекъсната функция). Ако функцията f (x) е непрекъсната на интервала [a, b], то тя е ограничена на този интервал, т.е. има число C > 0 такова, че "x O [a, b] неравенството | f (x)| ≤ C е в сила.
Теорема 2(Вайерщрасе). Ако функцията f (x) е непрекъсната на интервала [a, b], тогава тя достига най-голямата си стойност M и най-малката си стойност m на този интервал, т.е. има точки α, β O [a, b], така че m = f (α) ≤ f (x) ≤ f (β) = M за всички x O [a, b] (фиг. 2).

Най-голямата стойност на М е обозначена със символа max x O [a, b] f (x), а най-малката стойност на m е символ min x O [a, b] f(x).
Теорема 3(за съществуването на нула). Ако функцията f (x) е непрекъсната на интервала [a, b] и приема ненулеви стойности на различни знаци в краищата на сегмента, тогава на интервала (a, b) има поне една точка ξ, при което f (ξ) = 0.
Геометрично значениетеорема е, че графиката на функция, която удовлетворява условията на теоремата, непременно ще пресича оста ОХ(фиг. 3).

| f(x) = 0, | (1) |
Теорема 4(Болцано–Коши). Ако функцията f (x) е непрекъсната в интервала [a, b], тогава тя приема (a, b) всички междинни стойности между f (a) и f (b).
Наличие на непрекъсната обратна функция
Нека функцията y = f (x) е дефинирана, строго монотонна и непрекъсната на интервала [a, b]. Тогава на интервала [α, β] (α = f (a), β = f (b)) съществува обратна функция x = g (y), която също е строго монотонна и непрекъсната на интервала (α, β ).
Непрекъснатост на елементарни функции
Теоремите за непрекъснатостта на функциите следват директно от съответните теореми за границите.
Теорема.Сумата, произведението и частното на две непрекъснати функции е непрекъсната функция (за частното, с изключение на онези стойности на аргумента, в които делителят е нула).
Теорема.Нека функциите u= φ (х) е непрекъсната в точката х 0 и функцията г = f(u) е непрекъсната в точката u 0 = φ (х 0). След това сложната функция f(φ (х)), състоящ се от непрекъснати функции, е непрекъснат в точката х 0 .
Теорема.Ако функцията при = f(х) е непрекъсната и строго монотонна върху [ А; b] брадви о, след това обратната функция при = φ (х) също е непрекъснат и монотонен на съответния сегмент [ ° С;д] брадви OU(няма доказателство).
Функциите, които са непрекъснати на интервал, имат редица важни свойства. Нека ги формулираме под формата на теореми, без да даваме доказателства.
Теорема (Вайерщрас). Ако функцията е непрекъсната на сегмент, тогава тя достига своите максимални и минимални стойности на този сегмент.
Функцията, показана на фигура 5 при = f(х) е непрекъснат на интервала [ А; b], приема максималната си стойност Мв точката х 1 и най-малката м-в точката х 2. За всеки х [А; b] неравенството е в сила м ≤ f(х) ≤ М.

Последица.Ако една функция е непрекъсната на интервал, тогава тя е ограничена на този интервал.
Теорема (Болцано - Коши).Ако функцията при= f(х) е непрекъснат на интервала [ а; b] и приема неравни стойности в краищата си f(а) = АИ f(b) = =IN, тогава на този сегмент той приема всички междинни стойности между АИ IN.
Геометрично теоремата е очевидна (виж фиг. 6).

За произволен номер СЪС, сключен между АИ IN, има смисъл свътре в този сегмент, така че f(с) = СЪС. Направо при = СЪСпресича графиката на функцията поне в една точка.
Последица.Ако функцията при = f(х) е непрекъснат на интервала [ А; b] и в краищата му приема стойности на различни знаци, след това вътре в сегмента [ А; b] има поне една точка с, в който тази функция f(х) отива на нула: f(с) = 0.
Геометричен смисъл на теоремата: ако графиката на непрекъсната функция минава от едната страна на оста окъм другата, тогава тя пресича оста вол(виж Фиг. 7).
 Ориз. 7.
Ориз. 7.