Линейната, особено линейната полиномна апроксимация често не отговаря на естеството на функцията. Например, полином с висока степен расте бързо и следователно дори проста функция е слабо апроксимирана от полинома на голям сегмент. Тъй като апроксимацията се извършва в широк диапазон от промени в аргумента, използването на нелинейна зависимост от коефициентите е дори по-изгодно тук, отколкото при интерполацията.
На практика се използват два вида зависимости. Едната е квазилинейна зависимост, намалена чрез изравняваща промяна на променливите до линейна, която беше подробно изследвана в предишните параграфи. Този метод е много ефективен и често се използва при обработка на експерименти, тъй като априорната информация за физиката на процеса помага да се намери добра замяна на променливите. Просто трябва да имаме предвид, че приближението, което е най-добро в новите променливи, няма да бъде най-доброто в смисъла на скаларното произведение в старите променливи. Следователно трябва да се обърне специално внимание на избора на тегла в новите променливи.
Класически пример е проблемът с радиоактивното разпадане на облъчена проба, в която удобните променливи и t, където е скоростта на разпадане. При тези променливи кривата обикновено се апроксимира с прекъсната линия, чиито връзки съответстват на разпада на все по-дълго живеещи членове на радиоактивната серия.
Друг често използван тип зависимост от коефициентите е дробно-линейна, когато апроксимиращата функция е рационална:
Често се използва и отношението на обобщените полиноми. Това приближение ни позволява да предадем полюсите на функцията - те съответстват на нулите на знаменателя на необходимата кратност. Често е възможно да се възпроизведе асимптотичното поведение при поради подходящия избор на количество, например, ако , тогава трябва да зададем . В този случай можете да ги вземете достатъчно големи, за да имате много коефициенти на приближение.
Въпреки това квадратната грешка вече няма да бъде квадратична функция на коефициентите, така че не е лесно да се намерят коефициентите на рационална функция. По аналогия със средноквадратичното приближение чрез полиноми, можем да предположим, че грешката има брой нули, не по-малък от броя на свободните коефициенти (сравнете със забележка 3 в параграф 2). Тогава проблемът се свежда до интерполация на Лагранж върху тези нули и коефициентите се намират от система от линейни уравнения:
Разбира се, точната позиция на нулите е неизвестна; те се избират на случаен принцип, обикновено равномерно разпределени в сегмента. Този метод се нарича метод на избраните точки. Приближението, получено с този метод, изобщо няма да е най-доброто.
Освен това методът на избраните точки е неразумен, както и всяка интерполация, ако има забележима грешка.
Най-доброто приближение може да се намери с помощта на метода на итерирано тегло. Имайте предвид, че задачата
се решава лесно: изразът отляво е квадратична функция на коефициентите и диференцирането по тях води до линейна система за определяне на коефициентите, подобна на (38). Новата задача се различава съществено от първоначалната по това, че вместо тежест се използва различно тегло, така че решението й не е най-доброто приближение. Нека напишем оригиналния проблем в нова форма:

и ще го решим чрез прост итеративен процес

може да се приеме за нулево приближение. При всяка итерация теглото е известно от предишната итерация, така че коефициентите се намират лесно от минималното условие на квадратната форма. Практиката показва, че коефициентите на най-доброто приближение слабо зависят от избора на тегло, така че итерациите обикновено се сближават бързо.
а) Разгледайте някои примери за приближение чрез рационална функция. Да сложим
замествайки първите два члена на редицата с дроб, получаваме . Тази проста формула гарантира точност и е много удобна за оценки.
б) В теорията на вероятностите важна роля играе интегралът на грешката, за който са известни разширенията на серията:

Първата серия се сближава абсолютно, но при сближаване е много бавно; втората серия се сближава асимптотично за големи стойности на . Заменяйки първите членове на всяка серия с дроби, получаваме

В посочените диапазони на изменение на аргумента грешката на първата формула не надвишава 0,4%, а грешката на втората формула не надвишава 2,4%. По този начин точността на тези приближения е достатъчна за много практически приложения.
c) Нека поставим при . Тази функция е монотонна и за нея е лесно да се конструира дроб
![]()
(Моля, обърнете внимание на допълнителния раздел от 06/04/2017 в края на статията.)
Счетоводство и контрол! Тези над 40 трябва добре да помнят този лозунг от времето на изграждането на социализма и комунизма у нас.
Но без добре изградено счетоводство е невъзможно ефективното функциониране на държава, регион, предприятие или домакинство в нито една социално-икономическа формация на обществото! За изготвяне на прогнози и планове за дейност и развитие са необходими изходни данни. Къде мога да ги взема? Само един надежденизточникът е твоястатистически записи за предишни периоди от време.
Според мен всеки разумен човек трябва да вземе предвид резултатите от своята дейност, да събира и записва информация, да обработва и анализира данни и да прилага резултатите от анализа, за да взема правилни решения в бъдеще. Това не е нищо повече от натрупване и рационално използване на житейския опит. Ако не поддържате записи на важни данни, след определен период от време ще ги забравите и когато започнете отново да се занимавате с тези проблеми, отново ще направите същите грешки, които сте направили, когато сте направили това за първи път.
„Спомням си, че преди 5 години произвеждахме до 1000 броя такива продукти на месец, а сега едва успяваме да сглобим 700!“ Отваряме статистиката и виждаме, че преди 5 години дори не са произвели 500 броя...
„Колко струва един километър от вашата кола, като се вземе предвид всекиразходи? Да отворим статистиката – 6 рубли/км. Пътуване до работа - 107 рубли. По-евтино от вземането на такси (180 рубли) с повече от един и половина пъти. А имаше моменти, когато беше по-евтино да вземеш такси...
„Колко време отнема производството на стоманените конструкции на 50-метрова ъглова комуникационна кула?“ Отваряме статистиката - и след 5 минути отговорът е готов...
„Колко ще струва ремонтът на стая в апартамент?“ Изваждаме стари записи, правим корекция за инфлацията през последните години, вземаме предвид, че последния път сме закупили материали с 10% по-евтини от пазарната цена и вече знаем прогнозната цена...
Водейки записи за професионалните си дейности, винаги ще сте готови да отговорите на въпроса на шефа си: „Кога!!!???“ Чрез воденето на домакинска документация е по-лесно да планирате разходи за големи покупки, ваканции и други разходи в бъдеще, като вземете подходящи мерки за получаване на допълнителен доход или за намаляване на ненужните разходи днес.
В тази статия ще използвам прост пример, за да покажа как събраните статистически данни могат да бъдат обработени в Excel за по-нататъшно използване при прогнозиране на бъдещи периоди.
Апроксимация на статистически данни в Excel с аналитична функция.
Производственият обект произвежда строителни метални конструкции от ламарина и профилни изделия. Обектът работи стабилно, поръчките са еднотипни, броят на работниците варира леко. Има данни за продукцията за предходните 12 месеца и за количеството обработен прокат през тези периоди от време по групи: листове, I-образни греди, канали, ъгли, кръгли тръби, правоъгълни профили, кръгли продукти. След предварителен анализ на първоначалните данни възникна предположението, че общото месечно производство на метални конструкции значително зависи от броя на ъглите в поръчките. Нека проверим това предположение.
Първо, няколко думи за приближението. Ще търсим закон - аналитична функция, тоест функция, определена от уравнение, което по-добре от другите описва зависимостта на общата производителност на металните конструкции от количеството ъглова стомана в изпълнените поръчки. Това е приближение, а намереното уравнение се нарича апроксимираща функция за първоначалната функция, дадена под формата на таблица.
1. Включете Excel и поставете таблица със статистически данни върху лист.

2. След това изграждаме и форматираме диаграма на разсейване, в която по оста X задаваме стойностите на аргумента - броя на обработените ъгли в тонове. По оста Y нанасяме стойностите на първоначалната функция - общото производство на метални конструкции на месец, посочено в таблицата.

3. „Насочваме“ мишката към някоя от точките на диаграмата и щракваме с десния бутон, за да изведем контекстното меню (както казва един мой добър приятел - когато работите в непозната програма, когато не знаете какво да правите, щракнете по-често с десния бутон на мишката...). В падащото меню изберете „Добавяне на тренд линия...“.
4. В прозореца „Тенденция“, който се показва, в раздела „Тип“ изберете „Линеен“.


6. На графиката се появи права линия, апроксимираща нашата зависимост от таблицата.

В допълнение към самата линия виждаме уравнението на тази линия и, най-важното, виждаме стойността на параметъра R 2 - стойността на надеждността на приближението! Колкото по-близка е стойността му до 1, толкова по-точно избраната функция апроксимира табличните данни!
7. Ние изграждаме линии на тренд, използвайки степенни, логаритмични, експоненциални и полиномиални приближения по същия начин, както изградихме линейна линия на тренд.

От всички избрани функции, полином от втора степен приближава най-добре нашите данни, той има максимален коефициент на надеждност R 2 .
Искам обаче да ви предупредя! Ако вземете полиноми от по-високи степени, вероятно ще получите още по-добри резултати, но кривите ще имат заплетен вид... Тук е важно да разберем, че търсим функция, която има физическо значение. Какво означава това? Това означава, че се нуждаем от апроксимираща функция, която ще даде адекватни резултати не само в рамките на разглеждания диапазон от стойности на X, но и извън него, тоест ще отговори на въпроса: „Каква ще бъде производителността на металните конструкции, ако броят на обработените ъгли на месец е по-малко от 45 и повече от 168 тона! Затова не препоръчвам да се увличате с полиноми с високи степени и внимателно да избирате парабола (полином от втора степен)!
Така че трябва да изберем функция, която не само интерполира добре табличните данни в диапазона от стойности X = 45...168, но също така позволява адекватна екстраполация извън този диапазон. В този случай избирам логаритмична функция, въпреки че можете да изберете и линейна, тъй като е най-простата. В разглеждания пример при избора на линейно приближение в Excel грешките ще бъдат по-големи, отколкото при избора на логаритмично, но не много.
8. Премахваме всички линии на тренд от полето на диаграмата, с изключение на логаритмичната функция. За да направите това, щракнете с десния бутон върху ненужните редове и изберете „Изчистване“ от контекстното меню, което се показва.
9. Накрая ще добавим ленти за грешки към точките с таблични данни. За да направите това, щракнете с десния бутон върху някоя от точките на графиката и изберете „Форматиране на серия от данни…“ в контекстното меню и конфигурирайте данните в раздела „Y-грешки“, както е показано на фигурата по-долу.

10. След това щракнете с десния бутон върху някоя от линиите на диапазона на грешките, изберете „Форматиране на ленти за грешки…“ в контекстното меню и в прозореца „Форматиране на ленти за грешки“ в раздела „Изглед“, регулирайте цвета и дебелината на линиите.

Всички други обекти на диаграма се форматират по същия начин.Excel!
Крайният резултат от диаграмата е показан на следващата екранна снимка.

Резултати.
Резултатът от всички предишни действия беше получената формула за апроксимиращата функция y=-172.01*ln (x)+1188.2. Познавайки го и броя на ъглите в месечния набор от работи, е възможно с висока степен на вероятност (±4% - вижте лентите за грешки) да прогнозирате общото производство на метални конструкции за месеца! Например, ако планът за месеца е 140 тона ъгли, тогава общата продукция, при равни други условия, най-вероятно ще бъде 338 ± 14 тона.
За да се увеличи надеждността на приближението, трябва да има много статистически данни. Дванадесет двойки стойности не са достатъчни.
От практиката ще кажа, че намирането на апроксимираща функция с коефициент на надеждност R 2 >0,87 трябва да се счита за добър резултат. Отличен резултат е с R2 >0.94.
На практика може да е трудно да се идентифицира един най-важен определящ фактор (в нашия пример, масата на ъглите, обработени за един месец), но ако опитате, винаги можете да го намерите във всяка конкретна задача! Разбира се, общата продукция за един месец наистина зависи от стотици фактори, като се има предвид, че изисква значителни разходи за труд от стандартизатори и други специалисти. Но резултатът все пак ще бъде приблизителен! Така че струва ли си да правите разходи, когато има много по-евтино математическо моделиране!
В тази статия докоснах само върха на айсберга, наречен събиране, обработка и практическо използване на статистически данни. Надявам се да разбера дали съм успял или не да събудя интереса ви към тази тема от коментарите и оценките на статията в търсачките.
Повдигнатият въпрос за апроксимирането на функция на една променлива има широко практическо приложение в различни области на живота. Но решението на проблема с апроксимацията на функцията има много по-голямо приложение няколко независимипроменливи... Прочетете за това и повече в следващите статии в блога.
Абонирай се към съобщения на статии в прозореца, разположен в края на всяка статия или в прозореца в горната част на страницата.
Не забравяй потвърди абонирайте се, като кликнете върху връзката в писмо, което ще дойде при вас на посочената поща (може да пристигне в папката « Спам » )!!!
Ще прочета коментарите ви с интерес, скъпи читатели! пишете!
P.S. (04.06.2017 г.)
Много точна, красива замяна на таблични данни с просто уравнение.
Не сте доволни от получената точност на приближение (R 2<0,95) или вид и набор функций, предлагаемые MS Excel?
Дали размерите на израза и формата на линията на апроксимиращия полином с висока степен не са приятни за окото?
Моля, вижте страницата "", за да получите по-точен и компактен резултат от приближението на вашите таблични данни и да научите проста техника за решаване на проблеми с приближение с висока точност чрез функция на една променлива.

При използване на предложения алгоритъм на действие беше открита много компактна функция, която осигурява най-висока точност на приближение: R 2 =0,9963!!!
Числени методи за решаване на задачи
Радиофизика и електроника
(урок)
Воронеж 2009 г
Учебникът е изготвен в катедра Физическа електроника
Факултет на Воронежкия държавен университет.
Разглеждат се методи за решаване на проблеми, свързани с автоматизиран анализ на електронни схеми. Представени са основните понятия на теорията на графите. Дадена е матрично-топологична формулировка на законите на Кирхоф. Описани са най-известните матрично-топологични методи: методът на възловите потенциали, методът на контурните токове, методът на дискретните модели, хибридният метод, методът на променливите състояния.
1. Апроксимация на нелинейни характеристики. Интерполация. 6
1.1. Полиноми на Нютон и Лагранж 6
1.2. Сплайн интерполация 8
1.3. Метод на най-малките квадрати 9
2. Системи алгебрични уравнения 28
2.1. Системи линейни уравнения. Метод на Гаус. 28
2.2. Разредени системи уравнения. LU факторизация. 36
2.3. Решаване на нелинейни уравнения 37
2.4. Решаване на системи от нелинейни уравнения 40
2.5. Диференциални уравнения. 44
2. Методи за търсене на екстремум. Оптимизация. 28
2.1. Екстремни методи за търсене. 36
2.2. Пасивно търсене 28
2.3. Последователно търсене 36
2.4. Многомерна оптимизация 37
Литература 47
Апроксимация на нелинейни характеристики. Интерполация.
1.1. Полиноми на Нютон и Лагранж.
При решаването на много задачи става необходимо да се замени функция f, за която има непълна информация или формата на която е твърде сложна, с по-проста и по-удобна функция F, близка в един или друг смисъл до f, даваща нейното приблизително представителство. За апроксимация (апроксимация) се използват функции F, принадлежащи към определен клас, например алгебрични полиноми от дадена степен. Има много различни версии на проблема с приближението на функцията, в зависимост от това кои функции f се апроксимират, кои функции F се използват за приближение, как се разбира близостта на функциите f и F и т.н.
Един от методите за конструиране на приближени функции е интерполацията, когато се изисква в определени точки (интерполационни възли) стойностите на оригиналната функция f и апроксимиращата функция F да съвпадат.В по-общия случай стойностите на производните в дадени точки трябва да съвпадат.
Интерполацията на функции се използва за замяна на трудна за изчисляване функция с друга, която е по-лесна за изчисляване; за приблизително възстановяване на функция от нейните стойности в отделни точки; за числено диференциране и интегриране на функции; за числено решаване на нелинейни и диференциални уравнения и др.
Най-простият проблем с интерполацията е следният. За определена функция на сегмент се задават n+1 стойности в точки, които се наричат интерполационни възли. При което . Изисква се да се конструира интерполираща функция F(x), която приема същите стойности в интерполационните възли като f(x):
F(x 0) = f(x 0), F(x 1) = f(x 1), ... , F(x n) = f(x n)
Геометрично това означава намиране на крива от определен тип, минаваща през дадена система от точки (x i, y i), i = 0,1,…,n.
Ако стойностите на аргумента надхвърлят региона, тогава говорим за екстраполация - продължаването на функцията извън региона на нейната дефиниция.
Най-често функцията F(x) се конструира под формата на алгебричен полином. Има няколко представяния на алгебрични интерполационни полиноми.
Един от методите за интерполиране на функции, които приемат стойности в точки, е да се конструира полином на Лагранж, който има следната форма:
Степента на интерполационния полином, преминаващ през n+1 интерполационни възли, е равна на n.
От формата на полинома на Лагранж следва, че добавянето на нова възлова точка води до промяна във всички членове на полинома. Това е неудобството на формулата на Лагранж. Но методът на Лагранж съдържа минимален брой аритметични операции.
За конструиране на полиноми на Лагранж с нарастващи степени може да се използва следната итерационна схема (схема на Aitken).
Полиномите, минаващи през две точки (x i, y i), (x j, y j) (i=0,1,…,n-1; j=i+1,…,n), могат да бъдат представени по следния начин:
Полиноми, минаващи през три точки (x i, y i), (x j, y j), (x k, y k)
(i=0,…,n-2; j=i+1,…,n-1; k=j+1,…,n), може да се изрази чрез полиноми L ij и L jk:
Полиноми за четири точки (x i, y i), (x j, y j), (x k, y k), (x l, y l) се конструират от полиноми L ijk и L jkl:
Процесът продължава, докато се получи полином, който минава през n дадени точки.
Алгоритъмът за изчисляване на стойността на полинома на Лагранж в точка XX, прилагащ схемата на Aitken, може да бъде написан с помощта на оператора:
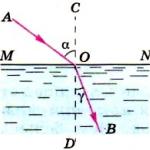
за (int i=0;i за (int i=0;i<=N-2;i++)Здесь не нужно слово int, программа ще се възприеме като грешка - повторно деклариране на променливата, променлива i вече е декларирана за (int j=i+1;j<=N-1;j++) F[j]=((arg-x[i])*F[j]-(arg-x[j])*F[i])/(x[j]-x[i]); където масивът F е междинните стойности на полинома на Лагранж. Първоначално F[I] трябва да се настрои равно на y i . След изпълнение на циклите, F[N] е стойността на полинома на Лагранж от степен N в точка XX. Друга форма за представяне на интерполационния полином са формулите на Нютон. Нека са равноотдалечени интерполационни възли; i=0,1,…,n ; - стъпка на интерполация. Първата интерполационна формула на Нютон, която се използва за интерполация напред, е: Наричани (крайни) разлики от i-ти ред. Те се дефинират така: Нормализиран аргумент. Когато интерполационната формула на Нютон се превръща в серия на Тейлър. Втората интерполационна формула на Нютон се използва за интерполация "назад": В последния запис вместо разлики (наречени разлики „напред“), се използват разлики „назад“: При неравномерно разположени възли, т.нар разделени различия В този случай интерполационният полином във формата на Нютон има формата За разлика от формулата на Лагранж, добавяне на нова двойка стойности. (x n +1, y n +1) тук се свежда до добавянето на един нов член. Следователно броят на интерполационните възли може лесно да се увеличи, без да се повтаря цялото изчисление. Това ви позволява да оцените точността на интерполацията. Формулите на Нютон обаче изискват повече аритметични операции от формулите на Лагранж. За n=1 получаваме формулата за линейна интерполация: За n=2 ще имаме формулата за параболична интерполация: Когато се интерполират функции, рядко се използват алгебрични полиноми с висока степен поради значителни изчислителни разходи и големи грешки в изчисляването на стойностите. В практиката най-често се използва частично линейна или частично параболична интерполация. При частично линейна интерполация функцията f(x) на интервала (i=0,1,…,n-1) се апроксимира от сегмент от права линия Алгоритъм за изчисление, който прилага частична линейна интерполация, може да бъде написан с помощта на оператора: за (int i=0;i if ((arg>=Fx[i]) && (arg<=Fx)) res=Fy[i]+(Fy-Fy[i])*(arg-Fx[i])/(Fx-Fx[i]); С помощта на първия цикъл търсим къде се намира желаната точка. С частична параболична интерполация, полиномът се конструира, като се използват 3-те възлови точки, които са най-близо до определената стойност на аргумента. Алгоритъмът за изчисление, който прилага частична параболична интерполация, може да бъде написан с помощта на оператора: за (int i=0;i y0=Fy; Когато i=0 елементът не съществува! x0=Fx; Същото res=y0+(y1-y0)*(arg-x0)/(x1-x0)+(1/(x2-x0))*(arg-x0)*(arg-x1)*(((y2-y1) /(x2-x1))-((y1-y0)/(x1-x0))); Използването на интерполация не винаги е препоръчително. При обработката на експериментални данни е желателно функцията да се изглади. Апроксимацията на експерименталните зависимости с помощта на метода на най-малките квадрати се основава на изискването за минимизиране на средната квадратична грешка Коефициентите на апроксимиращия полином се намират от решаване на система от m+1 линейни уравнения, т.нар. “нормални” уравнения, k=0,1,…,m В допълнение към алгебричните полиноми, тригонометричните полиноми се използват широко за приближаване на функции (вижте „числен хармоничен анализ“). Сплайновете са ефективно средство за приближаване на функция. Сплайнът изисква неговите стойности и производни в възлови точки да съвпадат с интерполираната функция f(x) и нейните производни до определен ред. Въпреки това, изграждането на сплайнове в някои случаи изисква значителни изчислителни разходи. Често е необходимо да има аналитични изрази за токово-напреженовите характеристики на нелинейните елементи. Тези изрази могат само приблизително да представят характеристиките ток-напрежение, тъй като физическите закони, които управляват връзките между напреженията и токовете в нелинейните устройства, не са изразени аналитично. Задачата за приблизително аналитично представяне на функция, определена графично или чрез таблица със стойности, в рамките на определени граници на промяна на нейния аргумент (независима променлива) се нарича апроксимация. В този случай, първо, се прави избор на апроксимираща функция, т.е. функция, с помощта на която приблизително се представя дадена зависимост, и, второ, изборът на критерий за оценка на „близостта“ на тази зависимост и функцията, която го приближава. Най-често като апроксимиращи функции се използват алгебрични полиноми, някои дробни рационални, експоненциални и трансцендентални функции или набор от линейни функции (отсечки от права линия). Ще приемем, че ток-напрежението на нелинейния елемент аз= забавление(ф)определени графично, т.е. определени във всяка точка от интервала Umin≤И≤Umax,и е еднозначна непрекъсната функция на променливата И.Тогава проблемът за аналитично представяне на характеристиката ток-напрежение може да се разглежда като проблем за приближаване на дадена функция ξ(x) чрез избрана апроксимираща функция f(х).
Относно близостта на приближаващото f(х) и приблизително ξ( х) функции или, с други думи, грешката на апроксимацията, обикновено се оценява по най-голямата абсолютна стойност на разликата между тези функции в интервала на апроксимация А≤ х≤ б,тоест по размер Δ=макс│ f(х)-
ξ( х)│
Често средната квадратична стойност на разликата между посочените функции в интервала на приближение се избира като критерий за близост. Понякога при близостта на две функции f( х) и ξ( х) разбират съвпадението в дадена точка x = хосамите функции и П+ 1 техни производни. Най-често срещаният начин за приближаване на аналитична функция до дадена е интерполация(метод на избраните точки), когато постигат съвпадение на функции f( х) и ξ( х) в избрани точки (при интерполация) X k , k= 0, 1, 2, ..., П.
Грешката на приближаване може да бъде постигната толкова по-малка, колкото по-голям е броят на разнообразните параметри, включени в апроксимиращата функция, т.е., например, колкото по-висока е степента на апроксимиращия полином или колкото по-голям е броят на правите сегменти, които съдържа апроксимиращата линейно-начупена функция . В същото време, естествено, обемът на изчисленията се увеличава, както при решаването на апроксимационния проблем, така и при последващия анализ на нелинейната верига. Простотата на този анализ, заедно с характеристиките на апроксимираната функция в рамките на интервала на апроксимация, служи като един от най-важните критерии при избора на типа апроксимираща функция. При проблемите с приближаването на характеристиките на токовото напрежение на електронните и полупроводниковите устройства, като правило, няма нужда да се стремим към висока точност на тяхното възпроизвеждане поради значителното разсейване на характеристиките на устройството от проба до проба и значителното влияние на дестабилизиращото фактори върху тях, например температура в полупроводникови устройства. В повечето случаи е достатъчно „правилно“ да се възпроизведе общият осреднен характер на зависимостта аз= f(u) в рамките на неговия работен диапазон. За да могат аналитично да се изчисляват вериги с нелинейни елементи е необходимо да има математически изрази за характеристиките на елементите. Самите тези характеристики обикновено са експериментални, т.е. получени в резултат на измервания на съответните елементи, след което на тази основа се формират референтни (типични) данни. Процедурата за математическо описание на дадена функция в математиката се нарича апроксимация на тази функция. Съществуват редица видове апроксимация: по избрани точки, по Тейлър, по Чебишев и т.н. В крайна сметка е необходимо да се получи математически израз, който да удовлетворява първоначалната апроксимираща функция с определени определени изисквания. Нека разгледаме най-простия метод: методът на избраните точки или възли на интерполация чрез степенен полином. Необходимо е да се определят коефициентите на полинома. За целта изберете (n+1)точки върху дадена функция и се съставя система от уравнения: От тази система се намират коефициентите a 0, a 1, a 2, …, a n.
В избраните точки апроксимиращата функция ще съвпадне с оригиналната, в други точки ще се различава (силно или не - зависи от степенния полином). Можете да използвате експоненциален полином: Втори метод: Метод на приближение на Тейлър
. В този случай се избира една точка, в която оригиналната функция ще съвпада с апроксимиращата, но се поставя допълнително условие в тази точка да съвпадат и производните. Приближение на Бътъруърт: избран е най-простият полином: В този случай можете да определите максималното отклонение ε
в краищата на диапазона. Приближение на Чебишев: е степенен закон, при който се установява съвпадение в няколко точки и максималното отклонение на апроксимиращата функция от оригиналната е сведено до минимум. В теорията на апроксимацията на функцията е доказано, че най-голямото отклонение в абсолютната стойност на полинома f(х)градуси Пот непрекъснатата функция ξ( х) ще бъде възможно най-малкото, ако в интервала на подход А≤ х≤ bразлика е( х) -
ξ( х) не по-малко от n + 2пъти взема своя последователно редуващ се максимален максимум f(х) -
ξ( х) = L> 0 и най-малкото f(х) -
ξ( х) = -Лстойности (критерий на Чебишев). В много приложни задачи се използва полиномна апроксимация, използваща средноквадратичен критерий за близост, когато параметрите на апроксимиращата функция f(х) се избират от условието за обръщане до минимум в интервала на приближение А≤ х≤ bквадрат на функционалното отклонение f(х) от дадена непрекъсната функция ξ( х), т.е. от условието: Λ=
1/b-a∫ a [ f(х)-
ξ( х)] 2 dx= мин. (7) В съответствие с правилата за намиране на екстремуми, решението на проблема се свежда до решаване на система от линейни уравнения, която се формира в резултат на приравняване на първите частични производни на функцията до нула Λ
за всеки от необходимите коефициенти a kапроксимиращ полином f(х),
т.е. уравнения dΛ ∕da 0=0; dΛ ∕da 1=0; dΛ ∕da 2=0, . . . , dΛ ∕da n=0. (8)
Доказано е, че тази система от уравнения също има уникално решение. В най-простите случаи се намира аналитично, а в общия случай - числено. Чебишев установи, че за максимални отклонения трябва да бъде изпълнено следното равенство: В инженерната практика т.нар частично линейно приближениее описание на дадена крива чрез прави сегменти. Във всеки от линеаризираните участъци на ток-напреженовата характеристика са приложими всички методи за анализ на трептенията в линейните електрически вериги. Ясно е, че колкото по-голям е броят на линеаризираните участъци, на които е разделена дадена характеристика ток-напрежение, толкова по-точно може да бъде апроксимирана и толкова по-голям е обемът на изчисленията по време на анализа на трептенията във веригата. В много приложни задачи за анализиране на трептения в нелинейни резистивни вериги, апроксимираната характеристика ток-напрежение в интервала на апроксимация се представя с достатъчна точност от два или три прави сегмента. Такова приближение на характеристиките на тока и напрежението дава в повечето случаи доста задоволителни резултати за точност за анализ на трептенията в нелинейна резистивна верига при "малки" магнитудни въздействия върху нелинейния елемент, т.е. когато моментните стойности на тока в нелинейния изменение на елемента в максимално допустимите граници от аз= 0 до аз = залюлявам се
1
| | | | | | | | | | | |

![]()