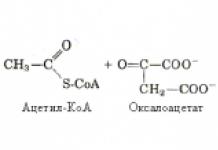
Разпределения на Pearson (хи-квадрат), Student и Fisher

С помощта на нормалното разпределение се дефинират три разпределения, които сега често се използват в статистическата обработка на данни. Тези разпределения се появяват много пъти в следващите раздели на книгата.

Разпределение на Пиърсън (хи - квадрат) – разпределение на случайна променлива

къде са случайните променливи X 1 , X 2 ,…, Xnнезависими и имат еднакво разпределение Н(0,1). В този случай броят на термините, т.е. п, се нарича „брой степени на свобода“ на разпределението хи-квадрат.

Разпределението хи-квадрат се използва, когато се оценява дисперсията (с помощта на доверителен интервал), когато се тестват хипотези за съгласие, хомогенност, независимост, предимно за качествени (категоризирани) променливи, които приемат краен брой стойности, и в много други задачи със статистически данни анализ.

Разпределение t t на Стюдънт е разпределението на случайна променлива

къде са случайните променливи UИ Xнезависим, Uима стандартно нормално разпределение Н(0,1) и X– чи разпределение – квадрат c пстепени на свобода. В същото време псе нарича „брой степени на свобода“ на разпределението на Стюдънт.

Студентското разпределение е въведено през 1908 г. от английския статистик У. Госет, който е работил във фабрика за бира. В тази фабрика са използвани вероятностни и статистически методи за вземане на икономически и технически решения, така че нейното ръководство забранява на В. Госет да публикува научни статии под собственото си име.

По този начин бяха защитени търговски тайни и „ноу-хау“ под формата на вероятностни и статистически методи, разработени от V. Gosset. Той обаче имаше възможност да публикува под псевдонима „Студент“. Историята на Gosset-Student показва, че дори преди сто години мениджърите във Великобритания са били наясно с по-голямата икономическа ефективност на вероятностно-статистическите методи.

В момента разпределението на Student е едно от най-известните разпределения, използвани при анализа на реални данни. Използва се при оценка на математическото очакване, прогнозната стойност и други характеристики с помощта на доверителни интервали, тестване на хипотези за стойностите на математическите очаквания, регресионни коефициенти, хипотези за хомогенност на извадката и др. .

къде са случайните променливи Разпределението на Фишер е разпределението на случайна променливаИ X 1са независими и имат хи-квадрат разпределение с броя на степените на свобода к 1 И к 2 съответно. В същото време двойката (к 1 , к 2 ) – двойка „степени на свобода“ от разпределението на Фишер, а именно, к 1 е броят на степените на свобода на числителя, и к 2 – брой степени на свобода на знаменателя. Разпределение на случайна величина Екръстен на великия английски статистик Р. Фишер (1890-1962), който активно го използва в трудовете си.

Разпределението на Фишер се използва при тестване на хипотези за адекватността на модела при регресионен анализ, равенство на дисперсиите и други проблеми на приложната статистика.

Изрази за хи-квадрат, функциите на разпределение на Стюдънт и Фишер, техните плътности и характеристики, както и таблиците, необходими за практическото им използване, могат да бъдат намерени в специализираната литература (вижте например).

Нека U 1, U 2, ..,U k са независими стандартни нормални стойности. Разпределението на случайната променлива K = U 1 2 +U 2 2 + .. + U k 2 се нарича разпределение хи-квадрат с кстепени на свобода (напишете K~χ 2 (k)). Това е унимодално разпределение с положителна асиметрия и следните характеристики: режим M=k-2 математическо очакване m=k дисперсия D=2k (фиг.). При достатъчно голяма стойност на параметъра кразпределението χ 2 (k) има приблизително нормално разпределение с параметри

При решаване на задачи на математическата статистика се използват критични точки χ 2 (k), в зависимост от дадената вероятност α и броя на степените на свобода к(Приложение 2). Критичната точка Χ 2 kr = Χ 2 (k; α) е границата на областта, вдясно от която лежи 100-α % от площта под кривата на плътността на разпределението. Вероятността стойността на случайната променлива K~χ 2 (k) по време на тестването да падне вдясно от точката χ 2 (k) не надвишава α P(K≥χ 2 kp)≤ α). Например за случайната променлива K~χ 2 (20) задаваме вероятността α=0,05. Използвайки таблицата на критичните точки на разпределението хи-квадрат (таблици), намираме χ 2 kp = χ 2 (20;0,05) = 31,4. Това означава, че вероятността на тази случайна променлива Квземете стойност, по-голяма от 31,4, по-малка от 0,05 (фиг.).

ориз. Графика на плътността на разпределение χ 2 (k) за различни стойности на броя на степените на свобода к

Критичните точки χ 2 (k) се използват в следните калкулатори:

1. Проверка за мултиколинеарност (относно мултиколинеарността).

Тестването на хипотеза с помощта на хи-квадрат ще отговори само на въпроса „има ли връзка?“ Необходими са допълнителни изследвания, за да се провери посоката на връзката. Освен това тестът Хи-квадрат има известна грешка при работа с нискочестотни данни.

Следователно, за да се провери посоката на връзката, се избира корелационен анализ, по-специално тестване на хипотезата с помощта на коефициента на корелация на Pearson с по-нататъшно тестване за значимост с помощта на t-теста.

За всяка стойност на нивото на значимост α Χ 2 може да се намери с помощта на функцията на MS Excel: =HI2OBR(α;степени на свобода)

n-1	.995	.990	.975	.950	.900	.750	.500	.250	.100	.050	.025	.010	.005
1	0.00004	0.00016	0.00098	0.00393	0.01579	0.10153	0.45494	1.32330	2.70554	3.84146	5.02389	6.63490	7.87944
2	0.01003	0.02010	0.05064	0.10259	0.21072	0.57536	1.38629	2.77259	4.60517	5.99146	7.37776	9.21034	10.59663
3	0.07172	0.11483	0.21580	0.35185	0.58437	1.21253	2.36597	4.10834	6.25139	7.81473	9.34840	11.34487	12.83816
4	0.20699	0.29711	0.48442	0.71072	1.06362	1.92256	3.35669	5.38527	7.77944	9.48773	11.14329	13.27670	14.86026
5	0.41174	0.55430	0.83121	1.14548	1.61031	2.67460	4.35146	6.62568	9.23636	11.07050	12.83250	15.08627	16.74960
6	0.67573	0.87209	1.23734	1.63538	2.20413	3.45460	5.34812	7.84080	10.64464	12.59159	14.44938	16.81189	18.54758
7	0.98926	1.23904	1.68987	2.16735	2.83311	4.25485	6.34581	9.03715	12.01704	14.06714	16.01276	18.47531	20.27774
8	1.34441	1.64650	2.17973	2.73264	3.48954	5.07064	7.34412	10.21885	13.36157	15.50731	17.53455	20.09024	21.95495
9	1.73493	2.08790	2.70039	3.32511	4.16816	5.89883	8.34283	11.38875	14.68366	16.91898	19.02277	21.66599	23.58935
10	2.15586	2.55821	3.24697	3.94030	4.86518	6.73720	9.34182	12.54886	15.98718	18.30704	20.48318	23.20925	25.18818
11	2.60322	3.05348	3.81575	4.57481	5.57778	7.58414	10.34100	13.70069	17.27501	19.67514	21.92005	24.72497	26.75685
12	3.07382	3.57057	4.40379	5.22603	6.30380	8.43842	11.34032	14.84540	18.54935	21.02607	23.33666	26.21697	28.29952
13	3.56503	4.10692	5.00875	5.89186	7.04150	9.29907	12.33976	15.98391	19.81193	22.36203	24.73560	27.68825	29.81947
14	4.07467	4.66043	5.62873	6.57063	7.78953	10.16531	13.33927	17.11693	21.06414	23.68479	26.11895	29.14124	31.31935
15	4.60092	5.22935	6.26214	7.26094	8.54676	11.03654	14.33886	18.24509	22.30713	24.99579	27.48839	30.57791	32.80132
16	5.14221	5.81221	6.90766	7.96165	9.31224	11.91222	15.33850	19.36886	23.54183	26.29623	28.84535	31.99993	34.26719
17	5.69722	6.40776	7.56419	8.67176	10.08519	12.79193	16.33818	20.48868	24.76904	27.58711	30.19101	33.40866	35.71847
18	6.26480	7.01491	8.23075	9.39046	10.86494	13.67529	17.33790	21.60489	25.98942	28.86930	31.52638	34.80531	37.15645
19	6.84397	7.63273	8.90652	10.11701	11.65091	14.56200	18.33765	22.71781	27.20357	30.14353	32.85233	36.19087	38.58226
20	7.43384	8.26040	9.59078	10.85081	12.44261	15.45177	19.33743	23.82769	28.41198	31.41043	34.16961	37.56623	39.99685
21	8.03365	8.89720	10.28290	11.59131	13.23960	16.34438	20.33723	24.93478	29.61509	32.67057	35.47888	38.93217	41.40106
22	8.64272	9.54249	10.98232	12.33801	14.04149	17.23962	21.33704	26.03927	30.81328	33.92444	36.78071	40.28936	42.79565
23	9.26042	10.19572	11.68855	13.09051	14.84796	18.13730	22.33688	27.14134	32.00690	35.17246	38.07563	41.63840	44.18128
24	9.88623	10.85636	12.40115	13.84843	15.65868	19.03725	23.33673	28.24115	33.19624	36.41503	39.36408	42.97982	45.55851
25	10.51965	11.52398	13.11972	14.61141	16.47341	19.93934	24.33659	29.33885	34.38159	37.65248	40.64647	44.31410	46.92789
26	11.16024	12.19815	13.84390	15.37916	17.29188	20.84343	25.33646	30.43457	35.56317	38.88514	41.92317	45.64168	48.28988
27	11.80759	12.87850	14.57338	16.15140	18.11390	21.74940	26.33634	31.52841	36.74122	40.11327	43.19451	46.96294	49.64492
28	12.46134	13.56471	15.30786	16.92788	18.93924	22.65716	27.33623	32.62049	37.91592	41.33714	44.46079	48.27824	50.99338
29	13.12115	14.25645	16.04707	17.70837	19.76774	23.56659	28.33613	33.71091	39.08747	42.55697	45.72229	49.58788	52.33562
30	13.78672	14.95346	16.79077	18.49266	20.59923	24.47761	29.33603	34.79974	40.25602	43.77297	46.97924	50.89218	53.67196

Брой степени на свобода к	Ниво на значимост a
	0,01	0,025	0.05	0,95	0,975	0.99
1	6.6	5.0	3.8	0.0039	0.00098	0.00016
2	9.2	7.4	6.0	0.103	0.051	0.020
3	11.3	9.4	7.8	0.352	0.216	0.115
4	13.3	11.1	9.5	0.711	0.484	0.297
5	15.1	12.8	11.1	1.15	0.831	0.554
6	16.8	14.4	12.6	1.64	1.24	0.872
7	18.5	16.0	14.1	2.17	1.69	1.24
8	20.1	17.5	15.5	2.73	2.18	1.65
9	21.7	19.0	16.9	3.33	2.70	2.09
10	23.2	20.5	18.3	3.94	3.25	2.56
11	24.7	21.9	19.7	4.57	3.82	3.05
12	26.2	23.3	21 .0	5.23	4.40	3.57
13	27.7	24.7	22.4	5.89	5.01	4.11
14	29.1	26.1	23.7	6.57	5.63	4.66
15	30.6	27.5	25.0	7.26	6.26	5.23
16	32.0	28.8	26.3	7.96	6.91	5.81
17	33.4	30.2	27.6	8.67	7.56	6.41
18	34.8	31.5	28.9	9.39	8.23	7.01
19	36.2	32.9	30.1	10.1	8.91	7.63
20	37.6	34.2	31.4	10.9	9.59	8.26
21	38.9	35.5	32.7	11.6	10.3	8.90
22	40.3	36.8	33.9	12.3	11.0	9.54
23	41.6	38.1	35.2	13.1	11.7	10.2
24	43.0	39.4	36.4	13.8	12.4	10.9
25	44.3	40.6	37.7	14.6	13.1	11.5
26	45.6	41.9	38.9	15.4	13.8	12.2
27	47.0	43.2	40.1	16.2	14.6	12.9
28	48.3	44.5	41.3	16.9	15.3	13.6
29	49.6	45.7	42.6	17.7	16.0	14.3
30	50.9	47.0	43.8	18.5	16.8	15.0

Тестът хи-квадрат е универсален метод за проверка на съответствието между резултатите от експеримента и използвания статистически модел.

Разстояние Пиърсън X 2

Пятницки А.М.

Руски държавен медицински университет

През 1900 г. Карл Пиърсън предлага прост, универсален и ефективен начин за тестване на съответствието между прогнозите на модела и експерименталните данни. „Хи-квадрат тестът“, който той предложи, е най-важният и най-често използван статистически тест. Повечето проблеми, свързани с оценката на неизвестните параметри на модела и проверката на съответствието между модела и експерименталните данни, могат да бъдат решени с негова помощ.

Нека има априори („предекспериментален“) модел на обекта или процеса, който се изучава (в статистиката те говорят за „нулевата хипотеза“ H 0) и резултатите от експеримент с този обект. Необходимо е да се реши дали моделът е адекватен (отговаря ли на реалността)? Експерименталните резултати противоречат ли на нашите идеи за това как работи реалността, или с други думи, трябва ли H0 да бъде отхвърлен? Често тази задача може да се сведе до сравняване на наблюдаваната (O i = Наблюдавана) и очакваната според модела (E i = Очаквана) средна честота на поява на определени събития. Смята се, че наблюдаваните честоти са получени в серия от N независими (!) наблюдения, направени при постоянни (!) условия. В резултат на всяко наблюдение се записва едно от М събития. Тези събития не могат да се случат едновременно (те са несъвместими по двойки) и задължително се случва едно от тях (комбинацията им образува надеждно събитие). Съвкупността от всички наблюдения се свежда до таблица (вектор) на честотите (O i )=(O 1 ,… O M ), която напълно описва резултатите от експеримента. Стойността O 2 =4 означава, че събитие номер 2 се е случило 4 пъти. Сума от честотите O 1 +… O M =N. Важно е да се прави разлика между два случая: N – фиксирана, неслучайна, N – случайна променлива. За фиксиран общ брой експерименти N, честотите имат полиномиално разпределение. Нека илюстрираме тази обща схема с прост пример.

Използване на теста хи-квадрат за тестване на прости хипотези.

Нека моделът (нулева хипотеза H 0) е, че зарът е справедлив - всички лица се появяват еднакво често с вероятност p i =1/6, i =, M=6. Проведен е експеримент, при който зарът е хвърлен 60 пъти (проведени са N = 60 независими опита). Според модела очакваме, че всички наблюдавани честоти O i на поява 1,2,... 6 точки трябва да бъдат близки до техните средни стойности E i =Np i =60∙(1/6)=10. Съгласно H 0, векторът на средните честоти (E i )=(Np i )=(10, 10, 10, 10, 10, 10). (Хипотези, при които средните честоти са напълно известни преди началото на експеримента, се наричат ​​прости.) Ако наблюдаваният вектор (O i ) е равен на (34,0,0,0,0,26), тогава той е незабавно ясно, че моделът е неправилен - костта не може да бъде правилна, тъй като само 1 и 6 са хвърлени 60 пъти за правилен зар е незначителна: P = (2/6) 60 =2,4*10 -29. Появата на такива явни разминавания между модела и опита обаче е изключение. Нека векторът на наблюдаваните честоти (O i ) е равен на (5, 15, 6, 14, 4, 16). Това съответства ли на H0? И така, трябва да сравним два честотни вектора (E i) и (O i). В този случай векторът на очакваните честоти (Ei) не е случаен, но векторът на наблюдаваните честоти (Oi) е случаен - по време на следващия експеримент (в нова серия от 60 хвърляния) той ще се окаже различен. Полезно е да се въведе геометрична интерпретация на проблема и да се приеме, че в честотното пространство (в този случай 6-измерно) са дадени две точки с координати (5, 15, 6, 14, 4, 16) и (10, 10, 10, 10, 10, 10 ). Достатъчно отдалечени ли са, за да се считат за несъвместими с H 0? С други думи, имаме нужда от:

1. научете се да измервате разстояния между честотите (точки в честотното пространство),
2. има критерий за това какво разстояние трябва да се счита за твърде („неправдоподобно“) голямо, тоест несъвместимо с H 0 .

Квадратът на обикновеното евклидово разстояние би бил равен на:

X 2 Евклид = С(O i -E i) 2 = (5-10) 2 +(15-10) 2 + (6-10) 2 +(14-10) 2 +(4-10) 2 +(16-10) 2

В този случай повърхностите X 2 Euclid = const винаги са сфери, ако фиксираме стойностите на E i и променим O i . Карл Пиърсън отбеляза, че не трябва да се използва използването на евклидово разстояние в честотното пространство. По този начин е неправилно да се приеме, че точките (O = 1030 и E = 1000) и (O = 40 и E = 10) са на равни разстояния една от друга, въпреки че и в двата случая разликата е O -E = 30. В крайна сметка, колкото по-висока е очакваната честота, толкова по-големи отклонения от нея трябва да се считат за възможни. Следователно точките (O =1030 и E =1000) трябва да се считат за „близки“, а точките (O =40 и E =10) за „далечни“ една от друга. Може да се покаже, че ако хипотезата H 0 е вярна, тогава флуктуациите на честотата O i спрямо E i са от порядъка на корен квадратен (!) от E i . Затова Пиърсън предлага, когато се изчислява разстоянието, да се повдигат на квадрат не разликите (O i -E i), а нормализираните разлики (O i -E i)/E i 1/2. И така, ето формулата за изчисляване на разстоянието на Пиърсън (това всъщност е квадрат на разстоянието):

X 2 Pearson = С((O i -E i )/E i 1/2) 2 = С(O i -E i ) 2 /E i

В нашия пример:

X 2 Pearson = (5-10) 2 /10+(15-10) 2 /10 +(6-10) 2 /10+(14-10) 2 /10+(4-10) 2 /10+( 16-10) 2 /10=15,4

За обикновен матрица всички очаквани честоти E i са еднакви, но обикновено са различни, така че повърхности, на които разстоянието на Пиърсън е постоянно (X 2 Pearson =const), се оказват елипсоиди, а не сфери.

Сега, когато формулата за изчисляване на разстоянията е избрана, е необходимо да разберем кои разстояния трябва да се считат за „не твърде големи“ (в съответствие с H 0), например, какво можем да кажем за разстоянието, което изчислихме 15.4 ? В какъв процент от случаите (или с каква вероятност) бихме получили разстояние, по-голямо от 15,4, когато провеждаме експерименти с обикновена матрица? Ако този процент е малък (<0.05), то H 0 надо отвергнуть. Иными словами требуется найти распределение длярасстояния Пирсона. Если все ожидаемые частоты E i не слишком малы (≥5), и верна H 0 , то нормированные разности (O i - E i )/E i 1/2 приближенно эквивалентны стандартным гауссовским случайным величинам: (O i - E i )/E i 1/2 ≈N (0,1). Это, например, означает, что в 95% случаев| (O i - E i )/E i 1/2 | < 1.96 ≈ 2 (правило “двух сигм”).

Обяснение. Броят на измерванията O i, попадащи в клетката на таблицата с номер i, има биномиално разпределение с параметрите: m =Np i =E i,σ =(Np i (1-p i)) 1/2, където N е числото от измерванията (N " 1), p i е вероятността едно измерване да попадне в дадена клетка (припомнете си, че измерванията са независими и се извършват при постоянни условия). Ако p i е малко, тогава: σ≈(Np i ) 1/2 =E i и биномиалното разпределение е близко до Поасон, при което средният брой наблюдения E i =λ и стандартното отклонение σ=λ 1/2 = E i 1/ 2. За λ≥5 разпределението на Поасон е близко до нормалното N (m =E i =λ, σ=E i 1/2 =λ 1/2), а нормализираната стойност (O i - E i )/E i 1 /2 ≈ N (0 ,1).

Pearson дефинира случайната променлива χ 2 n - „хи-квадрат с n степени на свобода“, като сумата от квадратите на n независими стандартни нормални случайни променливи:

χ 2 n = T 1 2 + T 2 2 + …+ T n 2 ,къде са всички T i = N(0,1) -п. О. r. с. V.

Нека се опитаме да разберем ясно значението на тази най-важна случайна променлива в статистиката. За да направим това, на равнината (с n = 2) или в пространството (с n = 3) представяме облак от точки, чиито координати са независими и имат стандартно нормално разпределениеf T (x) ~exp (-x 2 /2 ). В равнина, съгласно правилото за „две сигми“, което се прилага независимо и за двете координати, 90% (0,95*0,95≈0,90) точки се съдържат в квадрат (-2

f χ 2 2 (a) = Сexp(-a/2) = 0,5exp(-a/2).

При достатъчно голям брой степени на свобода n (n > 30), разпределението хи-квадрат се доближава до нормалното: N (m = n; σ = (2n) ½). Това е следствие от „теоремата за централната граница“: сумата от идентично разпределени количества с крайна вариация се доближава до нормалния закон с увеличаване на броя на членовете.

На практика трябва да запомните, че средният квадрат на разстоянието е равен на m (χ 2 n) = n, а неговата дисперсия е σ 2 (χ 2 n) = 2n. От тук е лесно да се заключи кои стойности на хи-квадрат трябва да се считат за твърде малки и твърде големи: по-голямата част от разпределението е в диапазона от n -2∙(2n) ½ до n +2∙(2n) ½.

Така че разстоянията на Пиърсън, значително надвишаващи n +2∙ (2n) ½, трябва да се считат за неправдоподобно големи (несъвместими с H 0). Ако резултатът е близък до n +2∙(2n) ½, тогава трябва да използвате таблици, в които можете да разберете точно в каква част от случаите могат да се появят такива и големи стойности на хи-квадрат.

Важно е да знаете как да изберете правилната стойност за броя на степените на свобода (съкратено n.d.f.). Изглежда естествено да се приеме, че n е просто равно на броя на цифрите: n =M. В статията си Пиърсън предлага това. В примера със заровете това би означавало, че n =6. Няколко години по-късно обаче се оказа, че Пиърсън греши. Броят на степените на свобода винаги е по-малък от броя на цифрите, ако има връзки между случайни променливи O i. За примера със зара, сумата O i е 60 и само 5 честоти могат да се променят независимо, така че правилната стойност е n = 6-1 = 5. За тази стойност на n получаваме n +2∙(2n) ½ =5+2∙(10) ½ =11,3. Тъй като 15.4>11.3, тогава хипотезата H 0 - зарът е правилен, трябва да бъде отхвърлена.

След изясняване на грешката съществуващите таблици χ 2 трябваше да бъдат допълнени, тъй като първоначално те нямаха случай n = 1, тъй като най-малкият брой цифри = 2. Сега се оказва, че може да има случаи, когато разстоянието на Пиърсън има разпределение χ 2 n =1.

Пример. При 100 хвърляния на монети броят на главите е O 1 = 65, а броят на опашките е O 2 = 35. Броят на цифрите е M = 2. Ако монетата е симетрична, тогава очакваните честоти са E 1 =50, E 2 =50.

X 2 Pearson = С(O i -E i) 2 /E i = (65-50) 2 /50 + (35-50) 2 /50 = 2*225/50 = 9.

Получената стойност трябва да се сравни с тези, които може да приеме случайната променлива χ 2 n =1, дефинирана като квадрат на стандартната нормална стойност χ 2 n =1 =T 1 2 ≥ 9 ó Т1 ≥3 или Т1 ≤-3. Вероятността за такова събитие е много ниска P (χ 2 n =1 ≥9) = 0,006. Следователно монетата не може да се счита за симетрична: H 0 трябва да се отхвърли. Фактът, че броят на степените на свобода не може да бъде равен на броя на цифрите, се вижда от факта, че сумата от наблюдаваните честоти винаги е равна на сумата от очакваните, например O 1 +O 2 =65+ 35 = E 1 +E 2 =50+50=100. Следователно произволни точки с координати O 1 и O 2 са разположени на права линия: O 1 +O 2 =E 1 +E 2 =100 и разстоянието до центъра се оказва по-малко, отколкото ако това ограничение не съществува и бяха разположени по цялата равнина. Наистина, за две независими случайни променливи с математически очаквания E 1 =50, E 2 =50, сумата от техните реализации не трябва винаги да е равна на 100 - например стойностите O 1 =60, O 2 =55 биха бъдете приемливи.

Обяснение. Нека сравним резултата от критерия на Pearson при M = 2 с това, което дава формулата на Moivre-Laplace при оценяване на случайни колебания в честотата на поява на събитие ν =K /N, имащо вероятност p в серия от N независими теста на Бернули ( K е броят на успехите):

χ 2 n =1 = С(O i -E i) 2 /E i = (O 1 -E 1) 2 /E 1 + (O 2 -E 2) 2 /E 2 = (Nν -Np) 2 /(Np) + (N ( 1-ν )-N (1-p )) 2 /(N (1-p ))=

=(Nν-Np) 2 (1/p + 1/(1-p))/N=(Nν-Np) 2 /(Np(1-p))=((K-Np)/(Npq) ½ ) 2 = T 2

Стойност T =(K -Np)/(Npq) ½ = (K -m (K))/σ(K) ≈N (0,1) със σ(K)=(Npq) ½ ≥3. Виждаме, че в този случай резултатът на Пиърсън съвпада точно с това, което дава нормалното приближение за биномиалното разпределение.

Досега разглеждахме прости хипотези, за които очакваните средни честоти E i са напълно известни предварително. За информация как да изберете правилния брой степени на свобода за сложни хипотези, вижте по-долу.

Използване на теста хи-квадрат за тестване на сложни хипотези

В примерите с обикновен зар и монета, очакваните честоти могат да бъдат определени преди (!) експеримента. Такива хипотези се наричат ​​„прости“. На практика "сложните хипотези" са по-често срещани. Освен това, за да се намерят очакваните честоти E i, е необходимо първо да се оцени една или няколко величини (параметри на модела) и това може да се направи само с помощта на експериментални данни. В резултат на това за „сложни хипотези“ очакваните честоти E i се оказват зависещи от наблюдаваните честоти O i и следователно самите те стават случайни променливи, вариращи в зависимост от резултатите от експеримента. В процеса на избор на параметри разстоянието на Пиърсън намалява - параметрите се избират така, че да се подобри съответствието между модела и експеримента. Следователно броят на степените на свобода трябва да намалее.

Как да оценим параметрите на модела? Има много различни методи за оценка - „метод на максималната правдоподобност“, „метод на моментите“, „метод на заместване“. Въпреки това не можете да използвате никакви допълнителни средства и да намерите оценки на параметрите чрез минимизиране на разстоянието на Пиърсън. В предкомпютърната ера този подход рядко се използва: той е неудобен за ръчни изчисления и като правило не може да бъде решен аналитично. Когато се изчислява на компютър, численото минимизиране обикновено е лесно за извършване и предимството на този метод е неговата гъвкавост. И така, според „метода за минимизиране на хи-квадрат“, ние избираме стойностите на неизвестните параметри, така че разстоянието на Пиърсън да стане най-малкото. (Между другото, като изучавате промените в това разстояние с малки измествания спрямо намерения минимум, можете да оцените мярката за точност на оценката: конструирайте доверителни интервали.) След като параметрите и самото това минимално разстояние са намерени, то е отново е необходимо да се отговори на въпроса дали е достатъчно малък.

Общата последователност от действия е следната:

1. Избор на модел (хипотеза H 0).
2. Избор на битове и определяне на вектора на наблюдаваните честоти O i .
3. Оценка на неизвестни параметри на модела и изграждане на доверителни интервали за тях (например чрез търсене на минималното разстояние на Пиърсън).
4. Изчисляване на очакваните честоти E i .
5. Сравнение на намерената стойност на разстоянието на Пиърсън X 2 с критичната стойност на хи-квадрат χ 2 crit - най-голямата, която все още се счита за правдоподобна, съвместима с H 0. Намираме стойността χ 2 crit от таблиците чрез решаване на уравнението

P (χ 2 n > χ 2 крит.)=1-α,

където α е „нивото на значимост“ или „размерът на критерия“ или „големината на грешката от първи тип“ (типична стойност α = 0,05).

Обикновено броят на степените на свобода n се изчислява по формулата

n = (брой цифри) – 1 – (брой параметри за оценка)

Ако X 2 > χ 2 crit, тогава хипотезата H 0 се отхвърля, в противен случай се приема. В α∙100% от случаите (т.е. доста рядко) този метод за проверка на H 0 ще доведе до „грешка от първи вид“: хипотезата H 0 ще бъде отхвърлена погрешно.

Пример.При изследване на 10 серии от 100 семена се преброява броят на заразените със зеленоока муха. Получени данни: O i =(16, 18, 11, 18, 21, 10, 20, 18, 17, 21);

Тук векторът на очакваните честоти е предварително неизвестен. Ако данните са хомогенни и получени за биномиално разпределение, тогава един параметър е неизвестен: делът p на заразените семена. Обърнете внимание, че в оригиналната таблица всъщност има не 10, а 20 честоти, които отговарят на 10 връзки: 16+84=100, ... 21+79=100.

X 2 = (16-100p) 2 /100p +(84-100(1-p)) 2 /(100(1-p))+...+

(21-100p) 2 /100p +(79-100(1-p)) 2 /(100(1-p))

Комбинирайки термини по двойки (както в примера с монета), получаваме формата на писане на критерия на Pearson, който обикновено се записва веднага:

X 2 = (16-100p) 2 /(100p(1-p))+…+ (21-100p) 2 /(100p(1-p)).

Сега, ако минималното разстояние на Пиърсън се използва като метод за оценка на p, тогава е необходимо да се намери p, за което X 2 = min. (Моделът се опитва, ако е възможно, да се „приспособи“ към експерименталните данни.)

Критерият на Пиърсън е най-универсалният от всички използвани в статистиката. Може да се прилага към едновариантни и многовариантни данни, количествени и качествени характеристики. Въпреки това, именно поради неговата универсалност, трябва да се внимава да не се правят грешки.

Важни точки

1.Избор на категории.

• Ако разпределението е дискретно, тогава обикновено няма произвол при избора на цифри.
• Ако разпределението е непрекъснато, произволът е неизбежен. Могат да се използват статистически еквивалентни блокове (всички O са еднакви, например =10). Дължините на интервалите обаче са различни. Когато правеха ръчни изчисления, те се опитаха да направят интервалите еднакви. Трябва ли интервалите при изследване на разпределението на едномерен признак да са равни? не
• Цифрите трябва да се комбинират по такъв начин, че очакваните (неспазени!) честоти да не са твърде малки (≥5). Нека припомним, че именно те (E i) са в знаменателите при изчисляването на X 2! При анализиране на едномерни характеристики е позволено да се наруши това правило в двете крайни цифри E 1 =E max =1. Ако броят на цифрите е голям и очакваните честоти са близки, тогава X 2 е добро приближение на χ 2 дори за E i =2.

Оценка на параметъра. Използването на „домашно приготвени“, неефективни методи за оценка може да доведе до завишени стойности на разстоянието на Пиърсън.

Избор на правилния брой степени на свобода. Ако оценките на параметрите се правят не от честотите, а директно от данните (например средната аритметична стойност се приема като оценка на средната), тогава точният брой степени на свобода n е неизвестен. Знаем само, че то удовлетворява неравенството:

(брой цифри – 1 – брой параметри, които се оценяват)< n < (число разрядов – 1)

Следователно е необходимо да се сравни X 2 с критичните стойности на χ 2 crit, изчислени в целия този диапазон от n.

Как да тълкуваме неправдоподобно малки стойности на хи-квадрат?Трябва ли една монета да се счита за симетрична, ако след 10 000 хвърляния попадне върху герба 5000 пъти? Преди това много статистици смятаха, че H 0 също трябва да бъде отхвърлен. Сега се предлага друг подход: приемете H 0, но подложите на допълнителна проверка данните и методологията за техния анализ. Има две възможности: или твърде малко разстояние на Пиърсън означава, че увеличаването на броя на параметрите на модела не е придружено от правилно намаляване на броя на степените на свобода, или самите данни са фалшифицирани (може би неволно коригирани към очаквания резултат).

Пример.Двама изследователи A и B изчисляват дела на рецесивните хомозиготи aa във второто поколение на монохибридно кръстосване AA * aa. Според законите на Мендел тази дроб е 0,25. Всеки изследовател проведе 5 експеримента, като във всеки експеримент бяха изследвани 100 организма.

Резултати A: 25, 24, 26, 25, 24. Заключението на изследователя: Законът на Мендел е верен (?).

Резултати B: 29, 21, 23, 30, 19. Заключение на изследователя: Законът на Мендел не е справедлив (?).

Законът на Мендел обаче е от статистическо естество и количественият анализ на резултатите обръща изводите! Комбинирайки пет експеримента в един, достигаме до разпределение хи-квадрат с 5 степени на свобода (тества се проста хипотеза):

X 2 A = ((25-25) 2 +(24-25) 2 +(26-25) 2 +(25-25) 2 +(24-25) 2)/(100∙0,25∙0,75)=0,16

X 2 B = ((29-25) 2 +(21-25) 2 +(23-25) 2 +(30-25) 2 +(19-25) 2)/(100∙0,25∙0,75)=5,17

Средна стойност m [χ 2 n =5 ]=5, стандартно отклонение σ[χ 2 n =5 ]=(2∙5) 1/2 =3,2.

Следователно, без справка с таблиците, е ясно, че стойността на X 2 B е типична, а стойността на X 2 A е неправдоподобно малка. Според таблици P (χ 2 n =5<0.16)<0.0001.

Този пример е адаптация на реален случай, случил се през 30-те години на миналия век (вижте работата на Колмогоров „За друго доказателство на законите на Мендел“). Интересното е, че изследовател А беше привърженик на генетиката, докато изследовател Б беше против нея.

Объркване в нотацията.Необходимо е да се разграничи разстоянието на Пиърсън, което изисква допълнителни конвенции при изчисляването му, от математическата концепция за случайна променлива хи-квадрат. Разстоянието на Пиърсън при определени условия има разпределение, близко до хи-квадрат с n степени на свобода. Следователно е препоръчително да НЕ се обозначава разстоянието на Пиърсън със символа χ 2 n, а да се използва подобно, но различно обозначение X 2. .

Критерият на Пиърсън не е всемогъщ.Има безкраен брой алтернативи за H 0, които той не е в състояние да вземе предвид. Да предположим, че тествате хипотезата, че характеристиката има равномерно разпределение, имате 10 цифри и векторът на наблюдаваните честоти е равен на (130,125,121,118,116,115,114,113,111,110). Критерият на Pearson не може да „забележи“, че честотите монотонно намаляват и H 0 няма да бъде отхвърлен. Ако беше допълнен с критерий за серия, тогава да!

Министерство на образованието и науката на Руската федерация

Федерална агенция за образование на град Иркутск

Байкалски държавен университет по икономика и право

Катедра "Информатика и кибернетика".

Хи-квадрат разпределение и неговите приложения

Колмикова Анна Андреевна

Студентка 2-ра година

група ИС-09-1

За обработка на получените данни използваме теста хи-квадрат.

За да направим това, ще изградим таблица на разпределението на емпиричните честоти, т.е. тези честоти, които наблюдаваме:

Теоретично очакваме, че честотите ще бъдат равномерно разпределени, т.е. честотата ще бъде разпределена пропорционално между момчета и момичета. Нека изградим таблица с теоретични честоти. За да направите това, умножете сумата на реда по сумата на колоната и разделете полученото число на общата сума (s).

Финалната таблица за изчисления ще изглежда така:

χ2 = ∑(E - T)² / T

n = (R - 1), където R е броят на редовете в таблицата.

В нашия случай хи-квадрат = 4,21; n = 2.

Използвайки таблицата с критични стойности на критерия, намираме: с n = 2 и ниво на грешка от 0,05, критичната стойност е χ2 = 5,99.

Получената стойност е по-малка от критичната стойност, което означава, че нулевата хипотеза е приета.

Извод: учителите не отдават значение на пола на детето, когато пишат характеристики за него.

Приложение

Критични точки на разпределението χ2

Таблица 1

Заключение

Студентите от почти всички специалности изучават раздела „Теория на вероятностите и математическа статистика” в края на курса по висша математика, в действителност те се запознават само с някои основни понятия и резултати, които очевидно не са достатъчни за практическа работа. Студентите се запознават с някои математически изследователски методи в специални курсове (например „Прогнозиране и технико-икономическо планиране“, „Технико-икономически анализ“, „Контрол на качеството на продуктите“, „Маркетинг“, „Контрол“, „Математически методи за прогнозиране“ ”), „Статистика“ и др. – при студенти от икономически специалности), но представянето в повечето случаи е много съкратено и шаблонно. В резултат на това знанията на специалистите по приложна статистика са недостатъчни.

Ето защо курсът „Приложна статистика” в техническите университети е от голямо значение, а курсът „Иконометрия” в икономическите университети, тъй като иконометрията, както е известно, е статистически анализ на конкретни икономически данни.

Теорията на вероятностите и математическата статистика предоставят фундаментални знания за приложна статистика и иконометрия.

Те са необходими на специалистите за практическа работа.

Разгледах непрекъснатия вероятностен модел и се опитах да покажа използването му с примери.

Списък на използваната литература

1. Орлов А.И. Приложна статистика. М.: Издателство "Изпит", 2004 г.

2. Гмурман В.Е. Теория на вероятностите и математическа статистика. М.: Висше училище, 1999. – 479 с.

3. Айвозян С.А. Теория на вероятностите и приложна статистика, том 1. М.: Единство, 2001. – 656 с.

4. Хамитов Г.П., Ведерникова Т.И. Вероятности и статистики. Иркутск: BGUEP, 2006 – 272 с.

5. Ежова Л.Н. Иконометрия. Иркутск: BGUEP, 2002. – 314 с.

6. Мостелер Ф. Петдесет забавни вероятностни задачи с решения. М.: Наука, 1975. – 111 с.

7. Мостелер Ф. Вероятност. М.: Мир, 1969. – 428 с.

8. Яглом А.М. Вероятност и информация. М.: Наука, 1973. – 511 с.

9. Чистяков В.П. Курс по теория на вероятностите. М.: Наука, 1982. – 256 с.

10. Кремер Н.Ш. Теория на вероятностите и математическа статистика. М.: ЕДИНСТВО, 2000. – 543 с.

11. Математическа енциклопедия, кн.1. М.: Съветска енциклопедия, 1976. – 655 с.

12. http://psystat.at.ua/ - Статистика в психологията и педагогиката. Статия Хи-квадрат тест.

Тестът \(\chi^2\) ("хи-квадрат", също "тест за съответствие на Пиърсън") има изключително широко приложение в статистиката. Най-общо можем да кажем, че се използва за тестване на нулевата хипотеза, че наблюдавана случайна променлива е обект на определен теоретичен закон за разпределение (за повече подробности вижте например). Конкретната формулировка на тестваната хипотеза ще варира в зависимост от случая.

В тази публикация ще опиша как работи критерият \(\chi^2\), като използвам (хипотетичен) пример от имунологията. Нека си представим, че сме провели експеримент, за да определим ефективността на потискане на развитието на микробно заболяване, когато в тялото се въведат подходящи антитела. В експеримента участваха общо 111 мишки, които разделихме на две групи, включващи съответно 57 и 54 животни. Първата група мишки получава инжекции от патогенни бактерии, последвани от въвеждане на кръвен серум, съдържащ антитела срещу тези бактерии. Животните от втората група послужиха за контрола - те получиха само бактериални инжекции. След известно време на инкубация се оказа, че 38 мишки са умрели, а 73 са оцелели. От загиналите 13 са от първа група, а 25 от втора (контролна). Нулевата хипотеза, тествана в този експеримент, може да бъде формулирана по следния начин: прилагането на серум с антитела няма ефект върху оцеляването на мишките. С други думи, ние твърдим, че наблюдаваните разлики в преживяемостта на мишките (77,2% в първата група срещу 53,7% във втората група) са напълно случайни и не са свързани с ефекта на антителата.

Получените в експеримента данни могат да бъдат представени под формата на таблица:

			Общо
Бактерии + серум
Само бактерии
Общо

Таблици като показаната се наричат ​​таблици за непредвидени случаи. В разглеждания пример таблицата е с размери 2x2: има два класа обекти („Бактерии + серум“ и „Само бактерии“), които се изследват по два критерия („Мъртви“ и „Оцелели“). Това е най-простият случай на таблица за непредвидени обстоятелства: разбира се, както броят на изучаваните класове, така и броят на функциите може да бъде по-голям.

За да тестваме нулевата хипотеза, посочена по-горе, трябва да знаем каква би била ситуацията, ако антителата действително нямаха ефект върху оцеляването на мишките. С други думи, трябва да изчислите очаквани честотиза съответните клетки от таблицата за непредвидени обстоятелства. Как да стане това? В експеримента са загинали общо 38 мишки, което е 34,2% от общия брой на участващите животни. Ако прилагането на антитела не повлиява преживяемостта на мишките, трябва да се наблюдава еднакъв процент на смъртност и в двете експериментални групи, а именно 34,2%. Изчислявайки колко е 34,2% от 57 и 54, получаваме 19,5 и 18,5. Това са очакваните нива на смъртност в нашите експериментални групи. Очакваните нива на оцеляване се изчисляват по подобен начин: тъй като са оцелели общо 73 мишки или 65,8% от общия брой, очакваните нива на оцеляване ще бъдат 37,5 и 35,5. Нека създадем нова таблица за непредвидени обстоятелства, сега с очакваните честоти:

	Мъртъв	Оцелели	Общо
Бактерии + серум
Само бактерии
Общо

Както виждаме, очакваните честоти са доста различни от наблюдаваните, т.е. прилагането на антитела изглежда има ефект върху оцеляването на мишки, заразени с патогена. Можем да определим количествено това впечатление с помощта на теста за съответствие на Pearson \(\chi^2\):

\[\chi^2 = \sum_()\frac((f_o - f_e)^2)(f_e),\]

където \(f_o\) и \(f_e\) са съответно наблюдаваните и очакваните честоти. Сумирането се извършва по всички клетки на таблицата. Така че за разглеждания пример имаме

\[\chi^2 = (13 – 19,5)^2/19,5 + (44 – 37,5)^2/37,5 + (25 – 18,5)^2/18,5 + (29 – 35,5)^2/35,5 = \]

Получената стойност на \(\chi^2\) достатъчно голяма ли е, за да отхвърли нулевата хипотеза? За да се отговори на този въпрос е необходимо да се намери съответната критична стойност на критерия. Броят на степените на свобода за \(\chi^2\) се изчислява като \(df = (R - 1)(C - 1)\), където \(R\) и \(C\) са числото на редове и колони в конюгацията на таблицата. В нашия случай \(df = (2 -1)(2 - 1) = 1\). Като знаем броя на степените на свобода, сега можем лесно да намерим критичната стойност \(\chi^2\), като използваме стандартната R функция qchisq() :

Така при една степен на свобода само в 5% от случаите стойността на критерия \(\chi^2\) надвишава 3,841. Стойността, която получихме, 6,79, значително надвишава тази критична стойност, което ни дава право да отхвърлим нулевата хипотеза, че няма връзка между прилагането на антитела и оцеляването на заразените мишки. Отхвърляйки тази хипотеза, рискуваме да сгрешим с вероятност по-малка от 5%.

Трябва да се отбележи, че горната формула за критерия \(\chi^2\) дава леко завишени стойности при работа с таблици за непредвидени обстоятелства с размер 2x2. Причината е, че разпределението на самия критерий \(\chi^2\) е непрекъснато, докато честотите на двоичните характеристики („умрял“ / „оцелял“) са по дефиниция дискретни. В тази връзка при изчисляване на критерия е прието да се въвежда т.нар корекция на непрекъснатостта, или Поправката на Йейтс :

\[\chi^2_Y = \sum_()\frac((|f_o - f_e| - 0,5)^2)(f_e).\]

Пиърсън "s Хи-квадрат тест с Йейтс"данни за корекция на непрекъснатостта: мишки X-квадрат = 5,7923, df = 1, p-стойност = 0,0161

Както виждаме, R автоматично прилага корекцията за непрекъснатост на Йейтс ( Хи-квадрат тест на Пиърсън с корекция за непрекъснатост на Йейтс). Стойността на \(\chi^2\), изчислена от програмата, беше 5,79213. Можем да отхвърлим нулевата хипотеза за липса на ефект на антитела с риск да сгрешим с вероятност от малко над 1% (p-стойност = 0,0161).