– броят на момчетата на 10 новородени.

Абсолютно ясно е, че този брой не е известен предварително и следващите десет родени деца може да включват:

Или момчета - един и единственот изброените опции.

И за да поддържате форма, малко физическо възпитание:

– скок на дължина (в някои единици).

Дори майстор на спорта не може да го предвиди :)

Вашите хипотези обаче?

2) Непрекъсната случайна променлива – приема всичкочислени стойности от някакъв краен или безкраен интервал.

Забележка : В учебна литературапопулярните съкращения DSV и NSV

Първо, нека анализираме дискретната случайна променлива, след това - непрекъснато.

Закон за разпределение на дискретна случайна величина

- Това кореспонденциямежду възможните стойности на това количество и техните вероятности. Най-често законът е написан в таблица:

Терминът се среща доста често ред разпространение, но в някои ситуации звучи двусмислено и затова ще се придържам към "закона".

И сега много важен момент: тъй като случайната променлива Задължителноще приеме една от ценностите, тогава се формират съответните събития пълна групаи сумата от вероятностите за тяхното възникване е равна на единица:

или, ако е написано съкратено:

Така например има законът за разпределение на вероятностите за точки, хвърлени на зара следващ изглед:

Без коментари.

Може да останете с впечатлението, че дискретна случайна променлива може да приема само „добри“ цели числа. Нека разсеем илюзията - те могат да бъдат всякакви:

Пример 1

Някои игри имат следния печеливш закон за разпределение:

...сигурно отдавна си мечтаете за такива задачи :) Ще ви издам една тайна - аз също. Особено след приключване на работата по теория на полето.

Решение: тъй като една случайна променлива може да вземе само един от три значения, тогава се формират съответните събития пълна група, което означава, че сумата от техните вероятности е равна на едно:

Разобличаване на „партизанина”:

– по този начин вероятността да спечелите конвенционални единици е 0,4.

Контрол: това е, което трябваше да се уверим.

Отговор:

Не е необичайно, когато трябва сами да съставите закон за разпределение. За това те използват класическо определение на вероятността, теореми за умножение/събиране за вероятности за събитияи други чипове тервера:

Пример 2

Кутията съдържа 50 лотарийни билета, сред които 12 са печеливши, като 2 от тях печелят по 1000 рубли, а останалите - по 100 рубли. Съставете закон за разпределение на случайна величина - размера на печалбата, ако един билет е изтеглен на случаен принцип от кутията.

Решение: както забелязахте, стойностите на случайна променлива обикновено се поставят в във възходящ ред. Затова започваме с най-малките печалби, а именно рубли.

Такива билетчета са общо 50 - 12 = 38, а съгл класическа дефиниция:
– вероятността произволно изтеглен билет да бъде губещ.

В други случаи всичко е просто. Вероятността да спечелите рубли е:

Проверка: – и това е особено приятен момент от такива задачи!

Отговор: желания закон за разпределение на печалбите:

Следваща задача за независимо решение:

Пример 3

Вероятността стрелецът да уцели целта е . Начертайте закон за разпределение на случайна променлива - брой попадения след 2 изстрела.

...Знаех си, че ти липсва :) Да си припомним теореми за умножение и събиране. Решението и отговорът са в края на урока.

Законът за разпределение напълно описва случайна променлива, но на практика може да бъде полезно (а понякога и по-полезно) да знаете само част от нея числови характеристики .

Очакване на дискретна случайна променлива

Говорейки на прост език, Това средна очаквана стойносткогато тестването се повтаря многократно. Нека случайната променлива приема стойности с вероятности съответно. Тогава математическото очакване на тази случайна променлива е равно на сбор от продуктитевсички негови стойности към съответните вероятности:

или свито:

Нека изчислим, например, математическото очакване на случайна променлива - броя точки, хвърлени на зара:

Сега нека си припомним нашата хипотетична игра:

Възниква въпросът: изгодно ли е изобщо да играете тази игра? ...кой има впечатления? Така че не можете да го кажете „на ръце“! Но на този въпрос може лесно да се отговори чрез изчисляване на математическото очакване, по същество - среднопретеглена стойностпо вероятност за печалба:

По този начин, математическото очакване на тази игра губещ.

Не вярвайте на впечатленията си - вярвайте на числата!

Да, тук можете да спечелите 10 или дори 20-30 пъти подред, но в дългосрочен план ни очаква неизбежна гибел. И не бих те посъветвал да играеш такива игри :) Е, може би само за забавление.

От всичко по-горе следва, че математическото очакване вече не е СЛУЧАЙНА стойност.

Творческа задачаЗа независими изследвания:

Пример 4

Г-н X играе европейска рулетка по следната система: той постоянно залага 100 рубли на „червено“. Съставете закон за разпределение на случайна променлива - нейните печалби. Изчислете математическото очакване на печалбите и го закръглете до най-близката копейка. Колко средно аритметичноИграчът губи ли за всеки сто, който е заложил?

справка : Европейската рулетка съдържа 18 червени, 18 черни и 1 зелен сектор („нула“). Ако се появи „червено“, на играча се изплаща двоен залог, в противен случай той отива към приходите на казиното

Има много други системи за рулетка, за които можете да създадете свои собствени вероятностни таблици. Но това е случаят, когато не се нуждаем от закони за разпределение или таблици, защото е установено със сигурност, че математическото очакване на играча ще бъде точно същото. Единственото нещо, което се променя от система на система е

Примери за случайни променливи, разпределени по нормален закон, са височината на човек и масата на уловената риба от същия вид. Нормалното разпределение означава следното : има стойности на човешкия ръст, масата на рибата от същия вид, които интуитивно се възприемат като „нормални“ (и всъщност осреднени), и в достатъчно голяма извадка те се срещат много по-често от тези, които се различават нагоре или надолу.

Нормалното вероятностно разпределение на непрекъсната случайна променлива (понякога разпределение на Гаус) може да се нарече камбанообразно поради факта, че функцията на плътността на това разпределение, симетрична спрямо средната стойност, е много подобна на разреза на камбана (червена крива на фигурата по-горе).

Вероятността да се срещнат определени стойности в извадката е равна на площта на фигурата под кривата и в случая нормална дистрибуциявиждаме, че под горната част на „камбаната“, която съответства на стойности, клонящи към средната, площта и следователно вероятността е по-голяма, отколкото под ръбовете. По този начин получаваме същото нещо, което вече беше казано: вероятността да срещнете човек с „нормален“ ръст и да хванете риба с „нормално“ тегло е по-висока, отколкото за стойности, които се различават нагоре или надолу. В много практически случаи грешките при измерване се разпределят по закон, близък до нормалния.

Нека погледнем отново фигурата в началото на урока, която показва функцията на плътност на нормално разпределение. Графиката на тази функция е получена чрез изчисляване на определена извадка от данни в пакета софтуер STATISTICA. На него колоните на хистограмата представляват интервали от извадкови стойности, чието разпределение е близко до (или, както обикновено се казва в статистиката, не се различава съществено от) действителната графика на функцията за плътност на нормалното разпределение, която е червена крива . Графиката показва, че тази крива наистина има формата на камбана.

Нормалното разпределение е ценно по много начини, защото като знаете само очакваната стойност на непрекъсната случайна променлива и нейното стандартно отклонение, можете да изчислите всяка вероятност, свързана с тази променлива.

Нормалното разпределение има и предимството, че е едно от най-лесните за използване. статистически тестове, използвани за проверка на статистически хипотези – t тест на Стюдънт- може да се използва само ако примерните данни се подчиняват на нормалния закон за разпределение.

Функция на плътност на нормалното разпределение на непрекъсната случайна променливаможе да се намери с помощта на формулата:

,

Където х- стойност на променящото се количество, - средна стойност, - стандартно отклонение, д=2,71828... - основа натурален логаритъм, =3,1416...

Свойства на функцията за плътност на нормалното разпределение

Промените в средната стойност преместват нормалната крива на функцията на плътността към оста вол. Ако се увеличи, кривата се премества надясно, ако намалява, след това наляво.

Ако стандартното отклонение се промени, височината на върха на кривата се променя. Когато стандартното отклонение нараства, върхът на кривата е по-висок, а когато намалява, е по-нисък.

Вероятност случайна променлива с нормално разпределение да попада в даден интервал

Още в този параграф ще започнем да решаваме практически проблеми, чийто смисъл е посочен в заглавието. Нека да разгледаме какви възможности предлага теорията за решаване на проблеми. Изходната концепция за изчисляване на вероятността случайна променлива с нормално разпределение да попадне в даден интервал е кумулативната функция на нормалното разпределение.

Кумулативна функция на нормалното разпределение:

.

Въпреки това е проблематично да се получат таблици за всяка възможна комбинация от средно и стандартно отклонение. Следователно един от прости начиниИзчисляването на вероятността случайна променлива с нормално разпределение да попадне в даден интервал е използването на вероятностни таблици за стандартизирано нормално разпределение.

Нормалното разпределение се нарича стандартизирано или нормализирано., чиято средна стойност е , а стандартното отклонение е .

Стандартизирана функция за плътност на нормалното разпределение:

.

Кумулативна функция на стандартизираното нормално разпределение:

.

Фигурата по-долу показва интегралната функция на стандартизираното нормално разпределение, чиято графика е получена чрез изчисляване на определена извадка от данни в софтуерния пакет STATISTICA. Самата графика е червена крива, а примерните стойности се доближават до нея.

За да увеличите снимката, можете да щракнете върху нея с левия бутон на мишката.

Стандартизирането на случайна променлива означава преминаване от оригиналните единици, използвани в задачата, към стандартизирани единици. Стандартизацията се извършва по формулата

На практика всички възможни стойности на случайна променлива често са неизвестни, така че стойностите на средното и стандартното отклонение не могат да бъдат определени точно. Те се заменят със средноаритметичната стойност на наблюденията и стандартното отклонение с. величина zизразява отклоненията на стойностите на случайна променлива от средната аритметична стойност при измерване на стандартните отклонения.

Отворен интервал

Таблицата на вероятностите за стандартизираното нормално разпределение, която може да се намери в почти всяка книга по статистика, съдържа вероятностите случайна променлива със стандартно нормално разпределение Зще приеме стойност, по-малка от определено число z. Тоест ще попадне в отворения интервал от минус безкрайност до z. Например, вероятността количеството Зпо-малко от 1,5, равно на 0,93319.

Пример 1.Компанията произвежда части, чийто експлоатационен живот е нормално разпределен със средно 1000 часа и стандартно отклонение от 200 часа.

За произволно избрана част изчислете вероятността животът й да бъде най-малко 900 часа.

Решение. Нека въведем първата нотация:

Желаната вероятност.

Стойностите на случайната променлива са в отворен интервал. Но ние знаем как да изчислим вероятността една случайна променлива да приеме стойност, по-малка от дадена, и според условията на задачата трябва да намерим такава, равна или по-голяма от дадена. Това е другата част от пространството под нормалната крива на плътност (камбана). Следователно, за да намерите желаната вероятност, трябва да извадите от единицата споменатата вероятност случайната променлива да приеме стойност, по-малка от зададените 900:

Сега случайната променлива трябва да бъде стандартизирана.

Продължаваме да въвеждаме нотацията:

z = (х ≤ 900) ;

х= 900 - зададена стойност на случайната променлива;

μ = 1000 - средна стойност;

σ = 200 - стандартно отклонение.

Използвайки тези данни, получаваме условията на проблема:

.

Според таблици на стандартизирана случайна променлива (граница на интервал) z= −0,5 съответства на вероятност от 0,30854. Извадете го от единицата и получете това, което се изисква в изложението на проблема:

Така че вероятността частта да има експлоатационен живот от поне 900 часа е 69%.

Тази вероятност може да се получи с помощта на функцията на MS Excel NORM.DIST (интегрална стойност - 1):

П(х≥900) = 1 - П(х≤900) = 1 - NORM.DIST(900; 1000; 200; 1) = 1 - 0,3085 = 0,6915.

За изчисленията в MS Excel - в един от следващите параграфи на този урок.

Пример 2.В даден град средният годишен семеен доход е нормално разпределена случайна променлива със средна стойност 300 000 и стандартно отклонение 50 000. Известно е, че доходът на 40% от семействата е по-малък от А. Намерете стойността А.

Решение. В този проблем 40% не е нищо повече от вероятността случайната променлива да вземе стойност от отворен интервал, която е по-малка от определена стойност, обозначена с буквата А.

За да намерите стойността А, първо съставяме интегралната функция:

Според условията на проблема

μ = 300000 - средна стойност;

σ = 50000 - стандартно отклонение;

х = А- количеството, което трябва да се намери.

Измисляне на равенство

.

От статистическите таблици намираме, че вероятността от 0,40 съответства на стойността на границата на интервала z = −0,25 .

Следователно ние създаваме равенството

и намерете решението му:

А = 287300 .

Отговор: 40% от семействата имат доходи под 287 300.

Затворен интервал

В много задачи се изисква да се намери вероятността нормално разпределена случайна променлива да приеме стойност в интервала от z 1 към z 2. Тоест ще попадне в затворен интервал. За да се решат такива проблеми, е необходимо да се намерят в таблицата вероятностите, съответстващи на границите на интервала, и след това да се намери разликата между тези вероятности. Това изисква изваждане на по-малката стойност от по-голямата. Примери за решения на тези често срещани проблеми са следните и от вас се иска да ги решите сами, след което можете да видите правилните решения и отговори.

Пример 3.Печалбата на предприятието за определен период е случайна величина, подчинена на нормалния закон за разпределение със средна стойност 0,5 млн. и стандартно отклонение 0,354. Определете с точност до два знака след десетичната запетая вероятността печалбата на предприятието да бъде от 0,4 до 0,6 c.u.

Пример 4.Дължината на изработения детайл е случайна величина, разпределена по нормалния закон с параметри μ =10 и σ =0,071. Намерете вероятността от дефекти с точност до два знака след десетичната запетая, ако допустимите размери на детайла трябва да бъдат 10±0,05.

Съвет: в този проблем, в допълнение към намирането на вероятността случайна променлива да попадне в затворен интервал (вероятността да получите недефектна част), трябва да извършите още едно действие.

ви позволява да определите вероятността стандартизираната стойност Зне по-малко -zи не повече +z, Където z- произволно избрана стойност на стандартизирана случайна променлива.

Приблизителен метод за проверка на нормалността на разпределение

Приблизителен метод за проверка на нормалността на разпределението на пробните стойности се основава на следното свойство на нормалното разпределение: коефициент на асиметрия β 1 и коефициент на ексцес β 2 са равни на нула.

Коефициент на асиметрия β 1 числено характеризира симетрията на емпиричното разпределение спрямо средната стойност. Ако коефициентът на асиметрия е нула, тогава средноаритметричната стойност, медианата и модата са равни: и кривата на плътността на разпределението е симетрична спрямо средната стойност. Ако коефициентът на асиметрия е по-малък от нула (β 1 < 0 ), тогава средноаритметичната стойност е по-малка от медианата, а медианата от своя страна е по-малка от режим () и кривата е изместена надясно (в сравнение с нормалното разпределение). Ако коефициентът на асиметрия е по-голям от нула (β 1 > 0 ), тогава средноаритметичната стойност е по-голяма от медианата, а медианата от своя страна, повече мода() И кривата е изместена наляво (в сравнение с нормалното разпределение).

Коефициент на ексцесия β 2 характеризира концентрацията на емпиричното разпределение около средноаритметичното по посока на оста Ойи степента на пик на кривата на плътността на разпределението. Ако коефициентът на ексцес е по-голям от нула, тогава кривата е по-удължена (в сравнение с нормалното разпределение)по оста Ой(графиката е по-заострена). Ако коефициентът на ексцес е по-малък от нула, тогава кривата е по-плоска (в сравнение с нормалното разпределение)по оста Ой(графиката е по-тъпа).

Коефициентът на асиметрия може да се изчисли с помощта на функцията SKOS на MS Excel. Ако проверявате един масив от данни, тогава трябва да въведете диапазона от данни в едно поле „Число“.

Коефициентът на ексцес може да се изчисли с помощта на функцията KURTESS на MS Excel. При проверка на един масив от данни е достатъчно също да въведете диапазона от данни в едно поле „Число“.

И така, както вече знаем, при нормално разпределение коефициентите на изкривяване и ексцес са равни на нула. Но какво ще стане, ако получим коефициенти на изкривяване от -0,14, 0,22, 0,43 и коефициенти на ексцес от 0,17, -0,31, 0,55? Въпросът е съвсем справедлив, тъй като на практика имаме работа само с приблизителни, примерни стойности на асиметрия и ексцес, които са обект на някакво неизбежно, неконтролирано разсейване. Следователно не може да се изисква тези коефициенти да бъдат строго равни на нула; те трябва да бъдат само достатъчно близки до нула. Но какво означава достатъчно?

Необходимо е да се сравнят получените емпирични стойности с приемливи стойности. За да направите това, трябва да проверите следните неравенства (сравнете стойностите на модулните коефициенти с критичните стойности - границите на зоната за тестване на хипотезата).

За коефициента на асиметрия β 1 .

ЗАКОН ЗА РАЗПРЕДЕЛЕНИЕ И ХАРАКТЕРИСТИКИ

СЛУЧАЙНИ ВЕЛИЧИНИ

Случайни променливи, тяхната класификация и методи за описание.

Случайна величина е величина, която в резултат на експеримент може да приеме една или друга стойност, но коя от тях не е предварително известна. Следователно за случайна променлива можете да посочите само стойности, една от които тя определено ще приеме в резултат на експеримент. По-нататък ще наричаме тези стойности възможни стойности на случайната променлива. Тъй като случайната променлива количествено характеризира случайния резултат от експеримент, тя може да се разглежда като количествена характеристикаслучайно събитие.

Обикновено се означават случайни променливи с главни буквиЛатинска азбука, например X..Y..Z, и възможните им значения - със съответните малки букви.

Има три вида случайни променливи:

Отделен; Непрекъснато; Смесени.

Отделене случайна променлива, чийто брой възможни стойности образува изброимо множество. От своя страна множество, чиито елементи могат да бъдат номерирани, се нарича изброимо. Думата "дискретен" идва от латинското discretus, което означава "прекъснат, състоящ се от отделни части".

Пример 1. Дискретна случайна променлива е броят на дефектните части X в партида от nпродукти. Наистина, възможните стойности на тази случайна променлива са поредица от цели числа от 0 до n.

Пример 2. Дискретна случайна променлива е броят на изстрелите преди първото попадение в целта. Тук, както в пример 1, възможните стойности могат да бъдат номерирани, въпреки че в ограничаващия случай възможната стойност е безкрайно голямо число.

Непрекъснатое случайна променлива, чиито възможни стойности непрекъснато запълват определен интервал от числовата ос, понякога наричан интервал на съществуване на тази случайна променлива. По този начин, на всеки краен интервал на съществуване, броят на възможните стойности на непрекъсната случайна променлива е безкрайно голям.

Пример 3. Непрекъсната случайна променлива е месечното потребление на електроенергия на предприятието.

Пример 4. Непрекъсната случайна променлива е грешката при измерване на височината с алтиметър. Нека от принципа на работа на висотомера е известно, че грешката е в диапазона от 0 до 2 м. Следователно интервалът на съществуване на тази случайна променлива е интервалът от 0 до 2 м.

Закон за разпределение на случайни величини.

Случайна променлива се счита за напълно определена, ако нейните възможни стойности са посочени на цифровата ос и законът за разпределение е установен.

Закон за разпределение на случайна величина е релация, която установява връзка между възможните стойности на случайна променлива и съответните вероятности.

За случайна променлива се казва, че е разпределена според даден закон или подчинена на даден закон за разпределение. Редица вероятности, функция на разпределение, плътност на вероятността и характеристична функция се използват като закони на разпределение.

Законът за разпределение дава пълно вероятно описание на случайна променлива. Съгласно закона за разпределение може да се прецени преди експеримента кои възможни стойности на случайна променлива ще се появяват по-често и кои по-рядко.

За дискретна случайна променлива законът за разпределение може да бъде зададен под формата на таблица, аналитично (под формата на формула) и графично.

Най-простата формаопределянето на закона за разпределение на дискретна случайна променлива е таблица (матрица), в която всички възможни стойности на случайната променлива и съответните им вероятности са изброени във възходящ ред, т.е.

Такава таблица се нарича серия на разпределение на дискретна случайна променлива. 1

Събития X 1, X 2,..., X n, състоящи се в това, че в резултат на теста случайната променлива X ще приеме стойностите съответно x 1, x 2,... x n, са непоследователни и единствените възможни (тъй като в таблицата са изброени всички възможни стойности на случайна променлива), т.е. образуват пълна група. Следователно сумата от техните вероятности е равна на 1. По този начин за всяка дискретна случайна променлива

(Тази единица по някакъв начин е разпределена между стойностите на случайната променлива, оттук и терминът „разпределение“).

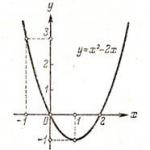
Серията на разпределение може да бъде изобразена графично, ако стойностите на случайната променлива са нанесени по абсцисната ос, а съответните им вероятности са нанесени по ординатната ос. Връзката на получените точки образува прекъсната линия, наречена многоъгълник или многоъгълник на вероятностното разпределение (фиг. 1).

ПримерЛотарията включва: автомобил на стойност 5000 den. бр., 4 телевизора на стойност 250 ден. единици, 5 видеорекордера на стойност 200 ден. единици За 7 дни са продадени общо 1000 билета. единици Съставете закон за разпределение на нетните печалби, получени от участник в лотарията, закупил един билет.

Решение. Възможните стойности на случайната променлива X - нетните печалби на билет - са равни на 0-7 = -7 пари. единици (ако билетът не е спечелил), 200-7 = 193, 250-7 = 243, 5000-7 = 4993 ден. единици (ако в билета има печалби съответно от видеорекордер, телевизор или кола). Като се има предвид, че от 1000 билета броят на непечелившите е 990, а посочените печалби са съответно 5, 4 и 1 и използвайки класическата дефиниция на вероятността, получаваме.

Нормален законвероятностни разпределения

Без преувеличение може да се нарече философски закон. Наблюдавайки различни обекти и процеси в света около нас, често се натъкваме на факта, че нещо не е достатъчно и че има норма:


Ето един основен изглед функции на плътностнормално разпределение на вероятностите и ви приветствам с добре дошли в този интересен урок.

Какви примери можете да дадете? Има просто тъмнина от тях. Това е например височината, теглото на хората (и не само), тяхната физическа сила, умствени способности и др. Има "основна маса" (по една или друга причина)и има отклонения и в двете посоки.

Това са различни характеристики на неодушевени предмети (еднакъв размер, тегло). Това е произволна продължителност на процесите, например времето на стометровото състезание или превръщането на смолата в кехлибар. От физиката си спомних молекулите на въздуха: някои от тях са бавни, други бързи, но повечето се движат със „стандартни“ скорости.

След това се отклоняваме от центъра с още едно стандартно отклонение и изчисляваме височината:

Маркиране на точки върху чертежа (зелен цвят)и виждаме, че това е напълно достатъчно.

На последния етап внимателно рисуваме графика и особено внимателноотразяват го изпъкнал/вдлъбнат! Вероятно отдавна сте разбрали, че оста x е хоризонтална асимптота, като е абсолютно забранено “катеренето” зад него!

При подаване на решение по електронен път е лесно да се създаде графика в Excel и неочаквано за мен дори записах кратко видео по тази тема. Но първо, нека поговорим за това как формата на нормалната крива се променя в зависимост от стойностите на и.

При увеличаване или намаляване на "а" (с постоянна „сигма“)графиката запазва формата си и се движи надясно/налявосъответно. Така например, когато функцията приеме формата и нашата графика се "премества" с 3 единици наляво - точно до началото на координатите:


Нормално разпределена величина с нулево математическо очакване получи напълно естествено име - центриран; неговата функция на плътност – дори, а графиката е симетрична спрямо ординатата.

В случай на промяна на "сигма" (с постоянно "а"), графиката „остава същата“, но променя формата си. Когато се увеличи, тя става по-ниска и удължена, като октопод, протягащ пипалата си. И, обратно, при намаляване на графиката става по-тесен и по-висок- оказва се „изненадан октопод“. Да, кога намаляване„сигма“ два пъти: предишната графика се стеснява и разтяга нагоре два пъти:

Всичко е в пълно съответствие с геометрични трансформации на графики.

Извиква се нормално разпределение с единична сигма стойност нормализиран, и ако е също центриран(нашият случай), тогава такова разпределение се нарича стандартен. Той има още по-проста функция за плътност, която вече е открита в Локална теорема на Лаплас: . Стандартната дистрибуция намери широко приложение в практиката и много скоро най-накрая ще разберем нейната цел.

Е, сега да гледаме филма:

Да, абсолютно точно - някак си незаслужено остана в сянка функция на разпределение на вероятностите. Да си спомним за нея определение:
– вероятността една случайна променлива да приеме стойност ПО-МАЛКА от променливата, която „минава през“ всички реални стойности до „плюс“ безкрайност.

Вътре в интеграла обикновено се използва различна буква, така че да няма „припокриване“ с нотацията, тъй като тук всяка стойност е свързана с неправилен интеграл , което е равно на някои номерот интервала.

Почти всички стойности не могат да бъдат изчислени точно, но както току-що видяхме, със съвременната изчислителна мощност това не е трудно. И така, за функцията стандартно разпределение, съответната функция на Excel обикновено съдържа един аргумент:

=NORMSDIST(з)

Едно, две - и готово:

Чертежът ясно показва изпълнението на всички свойства на функцията на разпределение, и от техническите нюанси тук трябва да обърнете внимание хоризонтални асимптотии инфлексната точка.

Сега нека си припомним един от ключови задачитеми, а именно ще разберем как да намерим вероятността нормална случайна променлива ще вземе стойността от интервала. Геометрично тази вероятност е равна на ■ площмежду нормалната крива и оста x в съответния участък:

но всеки път се опитвам да получа приблизителна стойност е неразумно и затова е по-рационално да се използва "лесна" формула:
.

! Също така помни , Какво

Тук можете да използвате Excel отново, но има няколко важни „но“: първо, не винаги е под ръка, и второ, „готовите“ стойности най-вероятно ще предизвикат въпроси от учителя. Защо?

Говорил съм за това много пъти преди: едно време (и не много отдавна) обикновеният калкулатор беше лукс, а „ръчният“ метод за решаване на въпросната задача все още е запазен в образователната литература. Нейната същност е да стандартизирамстойности „алфа“ и „бета“, т.е. намалете решението до стандартно разпределение:

Забележка : функцията се получава лесно от общия случайизползване на линеен замени. След това също:

и от извършената замяна формулата следва: преход от стойностите на произволно разпределение към съответните стойности на стандартно разпределение.

Защо е необходимо това? Факт е, че стойностите са били щателно изчислени от нашите предци и събрани в специална таблица, която е в много книги за terwer. Но още по-често има таблица със стойности, с която вече се занимавахме Интегрална теорема на Лаплас:

Ако имаме на наше разположение таблица със стойности на функцията на Лаплас , тогава решаваме чрез него:

Дробните стойности традиционно се закръглят до 4 знака след десетичната запетая, както се прави в стандартната таблица. И за контрол има Точка 5 оформление.

Напомням ви това , и за да избегнете объркване винаги контролирайте, таблица с КАКВА функция е пред очите ви.

Отговорсе изисква да се даде като процент, така че изчислената вероятност трябва да се умножи по 100 и резултатът да се предостави със смислен коментар:

– при полет от 5 до 70 м ще паднат приблизително 15,87% снаряди

Тренираме сами:

Пример 3

Диаметърът на фабрично изработените лагери е случайна променлива, нормално разпределена с математическо очакване от 1,5 см и стандартно отклонение от 0,04 см. Намерете вероятността размерът на произволно взет лагер да варира от 1,4 до 1,6 см.

В примерното решение и по-долу ще използвам функцията на Лаплас като най-често срещаната опция. Между другото, имайте предвид, че според формулировката краищата на интервала могат да бъдат включени в разглеждането тук. Това обаче не е критично.

И вече в този пример се натъкнахме на специален случай - когато интервалът е симетричен спрямо математическото очакване. В такава ситуация може да се напише във формата и, използвайки странността на функцията на Лаплас, да се опрости работната формула:

Делта параметърът се извиква отклонениеот математическото очакване и двойно неравенствомогат да бъдат „опаковани“ с помощта на модул:

– вероятността стойността на случайна променлива да се отклони от математическото очакване с по-малко от .

Добре че решението се побира в един ред :)
– вероятността диаметърът на произволно взет лагер да се различава от 1,5 cm с не повече от 0,1 cm.

Резултатът от тази задача се оказа близък до единица, но бих искал още по-голяма надеждност - а именно да открия границите, в които се намира диаметърът почти всекилагери. Има ли някакъв критерий за това? Съществува! На поставения въпрос отговаря т.нар

правило три сигма

Същността му е в това практически надежден е фактът, че нормално разпределена случайна променлива ще приеме стойност от интервала .

Наистина, вероятността за отклонение от очакваната стойност е по-малка от:
или 99.73%

Що се отнася до лагерите, това са 9973 броя с диаметър от 1,38 до 1,62 см и само 27 „нестандартни“ екземпляра.

В практическите изследвания обикновено се използва правилото на „трите сигми“. обратна посока: Ако статистическиУстановено е, че почти всички стойности изследвана случайна променливапопадат в интервал от 6 стандартни отклонения, тогава има убедителни причини да се смята, че тази стойност е разпределена по нормален закон. Проверката се извършва с помощта на теория статистически хипотези.

Продължаваме да решаваме тежките съветски проблеми:

Пример 4

Случайната стойност на грешката при претегляне се разпределя по нормалния закон с нулево математическо очакване и стандартно отклонение от 3 грама. Намерете вероятността следващото претегляне да бъде извършено с грешка, която не надвишава 5 грама по абсолютна стойност.

Решениемного просто. По условие веднага отбелязваме, че при следващото претегляне (нещо или някой)почти 100% ще получим резултата с точност до 9 грама. Но проблемът е с по-тясно отклонение и според формулата :

– вероятността следващото претегляне да бъде извършено с грешка, не по-голяма от 5 грама.

Отговор:

Решеният проблем е коренно различен от привидно подобен. Пример 3урок за равномерно разпределение. имаше грешка закръгляванерезултати от измерване, тук говорим за случайната грешка на самите измервания. Такива грешки възникват поради техническа характеристикасамото устройство (обхватът на допустимите грешки обикновено е посочен в неговия паспорт), а също и по вина на експериментатора - когато ние, например, „на око“ вземаме показания от иглата на същите везни.

Между другото има и т.нар систематиченгрешки при измерване. Вече е неслучайнигрешки, които възникват поради неправилна настройка или работа на устройството. Например нерегулираните подови везни могат стабилно да „добавят“ килограми, а продавачът систематично претегля клиентите. Или може да се изчислява не систематично. Във всеки случай обаче такава грешка няма да е случайна и нейното очакване е различно от нула.

…Спешно разработвам курс за обучение по продажби =)

Ние решаваме сами обратна задача:

Пример 5

Диаметърът на ролката е произволна нормално разпределена случайна променлива, нейното стандартно отклонение е равно на mm. Намерете дължината на интервала, симетричен по отношение на математическото очакване, в който е вероятно да попадне дължината на диаметъра на ролката.

Точка 5* дизайнерско оформлениеда помогна. Моля, имайте предвид, че тук математическото очакване не е известно, но това ни най-малко не ни пречи да решим задачата.

И изпитна задача, което силно препоръчвам за консолидиране на материала:

Пример 6

Случайна променлива с нормално разпределение се определя от нейните параметри (математическо очакване) и (стандартно отклонение). Задължително:

а) запишете плътността на вероятността и изобразете схематично нейната графика;
б) намерете вероятността да приеме стойност от интервала ;
в) намерете вероятността абсолютната стойност да се отклони от не повече от ;
г) използвайки правилото „три сигма“, намерете стойностите на случайната променлива.

Такива задачи се предлагат навсякъде и през годините практика съм решил стотици и стотици от тях. Не забравяйте да се упражнявате да рисувате рисунка на ръка и да използвате хартиени таблици;)

Е, ще ви дам пример повишена сложност:

Пример 7

Плътността на разпределение на вероятността на случайна променлива има формата . Намиране, математическо очакване, дисперсия, функция на разпределение, изграждане на графики на плътност и функции на разпределение, намиране.

Решение: Първо, нека отбележим, че условието не казва нищо за природата на случайната променлива. Наличието на показател само по себе си не означава нищо: може да се окаже, например, показателенили дори произволно непрекъснато разпространение. И следователно „нормалността“ на разпределението все още трябва да бъде оправдана:

Тъй като функцията определен при всякаквиреална стойност и тя може да бъде сведена до формата , тогава случайната променлива се разпределя по нормалния закон.

Ето ни. За това изберете пълен квадрати организирайте триетажна фракция:


Не забравяйте да извършите проверка, връщайки индикатора в оригиналната му форма:

, което искахме да видим.

По този начин:
- От правило за работа с правомощия"отщипвам" И тук можете веднага да запишете очевидните числени характеристики:

Сега нека намерим стойността на параметъра. Тъй като множителят на нормалното разпределение има формата и , тогава:
, откъдето изразяваме и заместваме в нашата функция:
, след което отново ще прегледаме записа с очите си и ще се уверим, че получената функция има формата .

Нека изградим графика на плътността:

и графика на функцията на разпределение :

Ако нямате Excel или дори обикновен калкулатор под ръка, тогава последната графика може лесно да бъде построена ръчно! В точката функцията на разпределение приема стойността и ето го

Функцията на разпределение на случайна променлива X е функцията F(x), която изразява за всяко x вероятността случайната променлива X да приеме стойността, по-малък х

Пример 2.5. Дадена е серия на разпределение на случайна променлива

Намерете и изобразете графично неговата функция на разпределение. Решение. Според дефиницията

F(jc) = 0 at хх

F(x) = 0,4 + 0,1 = 0,5 при 4 F(x) = 0,5 + 0,5 = 1 при х > 5.

И така (вижте Фиг. 2.1):

Свойства на функцията на разпределение:

1. Функцията на разпределение на случайна променлива е неотрицателна функция между нула и едно:

2. Функцията на разпределение на случайна променлива е ненамаляваща функция по цялата числена ос, т.е. при х 2 >x

3. При минус безкрайност функцията на разпределение е равна на нула, при плюс безкрайност е равна на единица, т.е.

4. Вероятност за попадение на случайна променлива хв интерваларавна на определен интегралот неговата плътност на вероятността, варираща от Апреди b(виж Фиг. 2.2), т.е.

Ориз. 2.2

3. Функцията на разпределение на непрекъсната случайна променлива (виж фиг. 2.3) може да се изрази чрез плътността на вероятността по формулата:

F(x)= Jp(*)*. (2.10)

4. Неправилен интеграл в безкрайни границина плътността на вероятността на непрекъсната случайна променлива е равна на единица:

Геометрични свойства / и 4 плътностите на вероятността означават, че нейната графика е крива на разпределение - лежи не под оста x, И цялата зонафигури, ограничена от кривата на разпределение и оста x, равно на едно.

За непрекъсната случайна променлива хочаквана стойност M(X)и дисперсия D(X)се определят по формулите:

(ако интегралът е абсолютно сходящ); или

(ако горните интеграли се събират).

Заедно с цифровите характеристики, отбелязани по-горе, концепцията за квантили и процентни точки се използва за описание на случайна променлива.

Квантилно ниво q(или q-квантил) е такава стойностx qслучайна величина, при което неговата функция на разпределение приема стойност, равно на q,т.е.

• 100Точката q%-ou е квантилът X~ q.
• ? Пример 2.8.

Въз основа на данните в пример 2.6 намерете квантила xqj и точката на 30% случайна променлива Х.

Решение. По дефиниция (2.16) F(xo t3)= 0.3, т.е.

~Y~ = 0,3, откъде идва квантилът? х 0 3 = 0,6. 30% случайна променлива точка х, или квантил X)_o,z = xoj"се намира по подобен начин от уравнението ^ = 0,7. където *, = 1,4. ?

Сред числените характеристики на случайна променлива има начален v* и централен R* моменти от k-ти ред, определени за дискретни и непрекъснати случайни променливи по формулите: