Решаване на квадратни неравенства - Хипермаркет на знанието. Линейни неравенства

Например неравенството е изразът \(x>5\).

Видове неравенства:

Ако \(a\) и \(b\) са числа или , тогава неравенството се извиква числови. Всъщност това е просто сравняване на две числа. Такива неравенства се разделят на веренИ неверен.

Например:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);

\(17+3\geq 115\) е неправилно числено неравенство, тъй като \(17+3=20\) и \(20\) е по-малко от \(115\) (и не е по-голямо или равно на) .

Ако \(a\) и \(b\) са изрази, съдържащи променлива, тогава имаме неравенство с променлива. Такива неравенства са разделени на видове в зависимост от съдържанието:

Какво е решението на едно неравенство?

Ако заместите число вместо променлива в неравенство, то ще се превърне в числово.

Ако дадена стойност за x превръща оригиналното неравенство в истинско числово, тогава то се извиква решение на неравенството. Ако не, тогава тази стойност не е решение. И към решаване на неравенство– трябва да намерите всички негови решения (или да покажете, че няма такива).

Например,ако заместим числото \(7\) в линейното неравенство \(x+6>10\), получаваме правилното числено неравенство: \(13>10\). И ако заместим \(2\), ще има неправилно числено неравенство \(8>10\). Тоест \(7\) е решение на първоначалното неравенство, но \(2\) не е.

Неравенството \(x+6>10\) обаче има и други решения. Наистина, ще получим правилните числени неравенства, когато заместим \(5\), и \(12\), и \(138\)... И как можем да намерим всички възможни решения? За това те използват За нашия случай имаме:

\(x+6>10\) \(|-6\)
\(x>4\)

Тоест всяко число, по-голямо от четири, е подходящо за нас. Сега трябва да запишете отговора. Решенията на неравенствата обикновено се записват числено, като допълнително се маркират върху числовата ос със засенчване. За нашия случай имаме:

Отговор: \(x\in(4;+\infty)\)

Кога се променя знакът на неравенството?

Има един голям капан в неравенствата, в който учениците наистина „обичат“ да попадат:

При умножаване (или деление) на неравенство с отрицателно число, то се обръща („повече“ с „по-малко“, „повече или равно“ с „по-малко или равно“ и т.н.)

Защо се случва това? За да разберем това, нека разгледаме трансформациите на численото неравенство \(3>1\). Вярно е, три наистина е по-голямо от едно. Първо нека се опитаме да го умножим по всяко положително число, например две:

\(3>1\) \(|\cdot2\)
\(6>2\)

Както виждаме, след умножението неравенството остава вярно. И без значение по какво положително число умножаваме, винаги ще получим правилното неравенство. Сега нека се опитаме да умножим по отрицателно число, например минус три:

\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)

Се случи фалшиво неравенство, защото минус девет е по-малко от минус три! Тоест, за да стане неравенството вярно (и следователно преобразуването на умножението с минус е било „законно“), трябва да обърнете знака за сравнение по следния начин: \(−9<− 3\).
С разделянето ще се получи по същия начин, можете да го проверите сами.

Правилото, написано по-горе, важи за всички видове неравенства, не само за числовите.

Отговор: \(x\in(-1;\infty)\)

Неравенства и увреждания

Неравенствата, точно като уравненията, могат да имат ограничения върху , тоест върху стойностите на x. Съответно тези стойности, които са неприемливи според DZ, трябва да бъдат изключени от обхвата на решенията.

Пример: Решете неравенството \(\sqrt(x+1)<3\)

Решение: Ясно е, че за да бъде лявата страна по-малка от \(3\), радикалният израз трябва да е по-малък от \(9\) (в края на краищата от \(9\) само \(3\)). Получаваме:

\(x+1<9\) \(|-1\)
\(х<8\)

Всичко? Всяка стойност на x, по-малка от \(8\), ще ни подхожда? Не! Защото ако вземем, например, стойността \(-5\), която изглежда отговаря на изискването, това няма да е решение на първоначалното неравенство, тъй като ще ни доведе до изчисляване на корен от отрицателно число.

\(\sqrt(-5+1)<3\)
\(\sqrt(-4)<3\)

Следователно трябва да вземем предвид и ограниченията за стойността на X - не може да има отрицателно число под корена. Така имаме второто изискване за x:

\(x+1\geq0\)
\(x\geq-1\)

И за да бъде x крайното решение, то трябва да отговаря на двете изисквания едновременно: трябва да е по-малко от \(8\) (за да бъде решение) и по-голямо от \(-1\) (за да е допустимо по принцип). Начертавайки го на числовата ос, имаме крайния отговор:

Отговор: \(\ляво[-1;8\дясно)\)

От вида ax 2 + bx + 0 0, където (вместо знака > може, разбира се, да има всеки друг знак за неравенство). Разполагаме с всички теоретични факти, необходими за решаване на такива неравенства, както ще видим сега.

Пример 1. Решете неравенство:

а) x 2 - 2x - 3 >0; б) x 2 - 2x - 3< 0;
в) х 2 - 2х - 3 > 0; г) x 2 - 2x - 3< 0.
Решение,

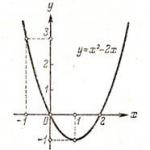
а) Разгледайте параболата y = x 2 - 2x - 3, показана на фиг. 117.

Решаването на неравенството x 2 - 2x - 3 > 0 означава отговор на въпроса при какви стойности на x ординатите на точките на параболата са положителни.

Отбелязваме, че y > 0, т.е. графиката на функцията е разположена над оста x, при x< -1 или при х > 3.

Това означава, че всички решения на неравенството са отворени точки лъч(- 00 , - 1), както и всички точки на отворения лъч (3, +00).

С помощта на знака U (знакът за комбиниране на множества) отговорът може да се запише по следния начин: (-00, - 1) U (3, +00). Отговорът обаче може да се запише така: x< - 1; х > 3.

б) Неравенство x 2 - 2x - 3< 0, или у < 0, где у = х 2 - 2х - 3, также можно решить с помощью рис. 117: графикразположен под оста x, ако -1< х < 3. Поэтому решениями данного неравенства служат все точки интервала (- 1, 3).

в) Неравенството x 2 - 2x - 3 > 0 се различава от неравенството x 2 - 2x - 3 > 0 по това, че отговорът трябва да включва и корените на уравнението x 2 - 2x - 3 = 0, т.е. точките x = - 1

и x = 3. По този начин решенията на това нестрого неравенство са всички точки от лъча (-00, - 1], както и всички точки от лъча.

Практичните математици обикновено казват следното: защо трябва внимателно да конструираме графика на парабола на квадратична функция, когато решаваме неравенството ax 2 + bx + c > 0

y = ax 2 + bx + c (както беше направено в пример 1)? Достатъчно е да направите схематична скица на графиката, за която просто трябва да намерите корениквадратичен трином (точката на пресичане на параболата с оста x) и определя дали клоновете на параболата са насочени нагоре или надолу. Тази схематична скица ще даде визуална интерпретация на решението на неравенството.

Пример 2.Решете неравенството - 2x 2 + 3x + 9< 0.
Решение.

1) Намерете корените на квадратния тричлен - 2x 2 + 3x + 9: x 1 = 3; х 2 = - 1,5.

2) Параболата, която служи като графика на функцията y = -2x 2 + 3x + 9, пресича оста x в точки 3 и - 1,5, а клоновете на параболата са насочени надолу, тъй като най-високата коефициент- отрицателно число - 2. На фиг. 118 показва скица на графиката.

3) С помощта на фиг. 118, заключаваме:< 0 на тех промежутках оси х, где график расположен ниже оси х, т.е. на открытом луче (-оо, -1,5) или на открытом луче C, +оо).
Отговор: x< -1,5; х > 3.

Пример 3.Решете неравенството 4x 2 - 4x + 1< 0.
Решение.

1) От уравнението 4x 2 - 4x + 1 = 0 намираме .

2) Квадратният тричлен има един корен; това означава, че параболата, служеща за графика на квадратен трином, не пресича оста x, а я докосва в точка . Клоните на параболата са насочени нагоре (фиг. 119.)

3) Използвайки геометричния модел, представен на фиг. 119 установяваме, че даденото неравенство е изпълнено само в точката, тъй като за всички останали стойности на x ординатите на графиката са положителни.
Отговор: .
Вероятно сте забелязали, че всъщност в примери 1, 2, 3, много специфичен алгоритъмрешение на квадратни неравенства, нека го формализираме.

Алгоритъм за решаване на квадратното неравенство ax 2 + bx + 0 0 (ax 2 + bx + c< 0)

Първата стъпка на този алгоритъм е да се намерят корените на квадратен трином. Но корените може да не съществуват, така че какво можем да направим? Тогава алгоритъмът не е приложим, което означава, че трябва да мислим по различен начин. Ключът към тези аргументи е даден от следните теореми.

С други думи, ако Д< 0, а >0, тогава неравенството ax 2 + bx + c > 0 е в сила за всички x; напротив, неравенството ax 2 + bx + c< 0 не имеет решений.
Доказателство. График функции y = ax 2 + bx + c е парабола, чиито клонове са насочени нагоре (тъй като a > 0) и която не пресича оста x, тъй като квадратният трином няма корени по условие. Графиката е показана на фиг. 120. Виждаме, че за всички x графиката е разположена над оста x, което означава, че за всички x е в сила неравенството ax 2 + bx + c > 0, което трябваше да се докаже.

С други думи, ако Д< 0, а < 0, то неравенство ах 2 + bх + с < 0 выполняется при всех х; напротив, неравенство ах 2 + bх + с >0 няма решения.

Доказателство. Графиката на функцията y = ax 2 + bx +c е парабола, чиито клонове са насочени надолу (тъй като a< 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 121. Видим, что при всех х график расположен ниже оси х, а это значит, что при всех х выполняется неравенство ах 2 + bх + с < 0, что и требовалось доказать.

Пример 4. Решете неравенство:

а) 2x 2 - x + 4 >0; б) -x 2 + 3x - 8 >0.

а) Намерете дискриминанта на квадратния тричлен 2x 2 - x + 4. Имаме D = (-1) 2 - 4 2 4 = - 31< 0.
Водещият коефициент на тринома (число 2) е положителен.

Това означава, че според теорема 1 за всички x е в сила неравенството 2x 2 - x + 4 > 0, тоест решението на даденото неравенство е цялото (-00, + 00).

б) Намерете дискриминанта на квадратния трином - x 2 + 3x - 8. Имаме D = 32 - 4 (- 1) (- 8) = - 23< 0. Старший коэффициент трехчлена (число - 1) отрицателен. Следовательно, по теореме 2, при всех х выполняется неравенство - х 2 + Зx - 8 < 0. Это значит, что неравенство - х 2 + Зх - 8 0 не выполняется ни при каком значении х, т. е. заданное неравенство не имеет решений.

Отговор: а) (-00, + 00); б) няма решения.

В следващия пример ще представим друг метод на разсъждение, който се използва за решаване на квадратни неравенства.

Пример 5.Решете неравенството 3x 2 - 10x + 3< 0.
Решение. Нека разложим на множители квадратния трином 3x 2 - 10x + 3. Корените на тринома са числата 3 и , така че като използваме ax 2 + bx + c = a (x - x 1)(x - x 2), получаваме 3x 2 - 10x + 3 = 3(x - 3) ( х - )
Нека отбележим корените на тричлена на числовата ос: 3 и (фиг. 122).

Нека x > 3; тогава x-3>0 и x->0, и следователно произведението 3(x - 3)(x - ) е положително. Следваща, нека< х < 3; тогда x-3< 0, а х- >0. Следователно произведението 3(x-3)(x-) е отрицателно. Накрая нека x<; тогда x-3< 0 и x- < 0. Но в таком случае произведение
3(x -3)(x -) е положително.

Обобщавайки разсъжденията, стигаме до извода: знаците на квадратния трином 3x 2 - 10x + 3 се променят, както е показано на фиг. 122. Интересуваме се от това, при колко x квадратният тричлен приема отрицателни стойности. От фиг. 122 заключаваме: квадратният трином 3x 2 - 10x + 3 приема отрицателни стойности за всяка стойност на x от интервала (, 3)
Отговор (, 3), или< х < 3.

Коментирайте. Методът на разсъждение, който използвахме в Пример 5, обикновено се нарича метод на интервалите (или метод на интервалите). Използва се активно в математиката за решаване рационаленнеравенства В 9 клас ще изучаваме по-подробно интервалния метод.

Пример 6. При какви стойности на параметъра p квадратно уравнение x 2 - 5x + p 2 = 0:
а) има два различни корена;

б) има един корен;

в) няма корени?

Решение. Броят на корените на квадратното уравнение зависи от знака на неговия дискриминант D. In в такъв случайнамираме D = 25 - 4р 2.

а) Квадратното уравнение има два различни корена, ако D>0, тогава задачата се свежда до решаване на неравенството 25 - 4р 2 > 0. Нека умножим двете страни на това неравенство по -1 (като не забравяме да сменим знака на неравенство). Получаваме еквивалентното неравенство 4p 2 - 25< 0. Далее имеем 4 (р - 2,5) (р + 2,5) < 0.

Знаците на израза 4(p - 2.5) (p + 2.5) са показани на фиг. 123.

Заключаваме, че неравенството 4(p - 2,5)(p + 2,5)< 0 выполняется для всех значений р из интервала (-2,5; 2,5). Именно при этих значениях параметра р данное квадратное уравнение имеет два различных корня.

б) квадратно уравнениеима един корен, ако D - 0.
Както установихме по-горе, D = 0 при p = 2,5 или p = -2,5.

Именно за тези стойности на параметъра p това квадратно уравнение има само един корен.

в) Квадратно уравнение няма корени, ако D< 0. Решим неравенство 25 - 4р 2 < 0.

Получаваме 4p 2 - 25 > 0; 4 (p-2.5)(p + 2.5)>0, откъдето (виж Фиг. 123) p< -2,5; р >2.5. За тези стойности на параметъра p това квадратно уравнение няма корени.

Отговор: а) при p (-2,5, 2,5);

б) при р = 2,5 или = -2,5;
в) на стр< - 2,5 или р > 2,5.

Мордкович А. Г., Алгебра. 8. клас: Учебник. за общо образование институции.- 3-то изд., преработ. - М.: Мнемозина, 2001. - 223 с.: ил.

Помагало за ученици онлайн, Математика за 8 клас изтегляне, календарно и тематично планиране

Решаване на неравенства онлайн

Преди да решавате неравенства, трябва да разберете добре как се решават уравнения.

Няма значение дали неравенството е строго () или нестрого (≤, ≥), първата стъпка е да решите уравнението, като замените знака за неравенство с равенство (=).

Нека обясним какво означава да се реши неравенство?

След като изучава уравненията, ученикът получава следната картина в главата си: той трябва да намери стойности на променливата, така че и двете страни на уравнението да приемат едни и същи стойности. С други думи, намерете всички точки, в които е валидно равенството. Всичко е точно!

Когато говорим за неравенства, имаме предвид намиране на интервали (отсечки), на които е валидно неравенството. Ако има две променливи в неравенството, тогава решението вече няма да бъде интервали, а някои области на равнината. Познайте сами какво ще бъде решението на неравенство в три променливи?

Как се решават неравенства?

За универсален начин за решаване на неравенства се счита методът на интервалите (известен още като метод на интервалите), който се състои в определяне на всички интервали, в границите на които ще бъде изпълнено дадено неравенство.

Без да навлизаме в вида на неравенството, в този случай това не е въпросът, трябва да решите съответното уравнение и да определите корените му, последвано от обозначаването на тези решения на числовата ос.

Как правилно да напиша решението на неравенство?

След като определите интервалите за решаване на неравенството, трябва да напишете правилно самото решение. Има важен нюанс - включени ли са границите на интервалите в решението?

Тук всичко е просто. Ако решението на уравнението удовлетворява ODZ и неравенството не е строго, тогава границата на интервала се включва в решението на неравенството. В противен случай не.

Разглеждайки всеки интервал, решението на неравенството може да бъде самият интервал, или полуинтервал (когато една от неговите граници удовлетворява неравенството), или сегмент - интервалът заедно с неговите граници.

Важен момент

Не си мислете, че само интервали, полуинтервали и отсечки могат да решат неравенството. Не, решението може да включва и отделни точки.

Например неравенството |x|≤0 има само едно решение - това е точка 0.

И неравенството |x|

Защо ви е необходим калкулатор за неравенство?

Калкулаторът за неравенства дава правилния краен отговор. В повечето случаи се предоставя илюстрация на числова ос или равнина. Вижда се дали границите на интервалите са включени в решението или не - точките се показват като защриховани или пунктирани.

Благодарение на онлайн калкулатора за неравенства можете да проверите дали правилно сте намерили корените на уравнението, маркирали сте ги на числовата ос и сте проверили изпълнението на условието за неравенство на интервалите (и границите)?

Ако вашият отговор се различава от отговора на калкулатора, тогава определено трябва да проверите повторно решението си и да идентифицирате грешката.

внимание!
Има допълнителни
материали в специален раздел 555.
За тези, които са много "не много..."
И за тези, които „много...“)

Какво стана "квадратно неравенство"?Няма въпрос!) Ако вземете всякаквиквадратно уравнение и сменете знака в него "=" (равно) на всеки знак за неравенство ( > ≥ < ≤ ≠ ), получаваме квадратно неравенство. Например:

1. x 2 -8x+12 ≥ 0

2. -x 2 +3x > 0

3. х 2 ≤ 4

Е, разбирате...)

Не напразно свързах уравнения и неравенства тук. Въпросът е, че първата стъпка в решаването всякаквиквадратно неравенство - реши уравнението, от което е съставено това неравенство.Поради тази причина невъзможността да се решават квадратни уравнения автоматично води до пълен провал в неравенствата. Подсказката ясна ли е?) Ако има нещо, вижте как се решават всякакви квадратни уравнения. Там всичко е описано подробно. И в този урок ще се занимаваме с неравенства.

Готовото за решаване неравенство има вида: отляво е квадратен тричлен брадва 2 +bx+c, вдясно - нула.Знакът за неравенство може да бъде абсолютно всичко. Първите два примера са тук вече са готови да вземат решение.Третият пример все още трябва да бъде подготвен.

Ако харесвате този сайт...

Между другото, имам още няколко интересни сайта за вас.)

Можете да практикувате решаване на примери и да разберете вашето ниво. Тестване с незабавна проверка. Да учим - с интерес!)

Можете да се запознаете с функции и производни.

Днес, приятели, няма да има сополи и сантименталности. Вместо това ще ви изпратя, без въпроси, в битка с един от най-страшните противници в курса по алгебра за 8-9 клас.

Да, разбрахте всичко правилно: говорим за неравенства с модул. Ще разгледаме четири основни техники, с които ще се научите да решавате около 90% от подобни проблеми. Какво ще кажете за останалите 10%? Е, ще говорим за тях в отделен урок. :)

Въпреки това, преди да анализирам някоя от техниките, бих искал да ви напомня два факта, които вече трябва да знаете. В противен случай рискувате изобщо да не разберете материала от днешния урок.

Това, което вече трябва да знаете

Captain Obviousness изглежда намеква, че за да решавате неравенства с модул, трябва да знаете две неща:

1. Как се решават неравенствата;
2. Какво е модул?

Да започнем с втората точка.

Дефиниция на модула

Тук всичко е просто. Има две дефиниции: алгебрична и графична. Като начало - алгебричен:

Определение. Модулът на число $x$ е или самото число, ако е неотрицателно, или противоположното му число, ако оригиналният $x$ все още е отрицателен.

Написано е така:

\[\ляво| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \right.\]

Говорейки на прост език, модулът е „число без минус“. И именно в тази двойственост (на някои места не е нужно да правите нищо с оригиналното число, но на други трябва да премахнете някакъв вид минус) е цялата трудност за начинаещите ученици.

Има ли още геометрична дефиниция. Също така е полезно да се знае, но ще се обърнем към него само в сложни и някои специални случаи, където геометричният подход е по-удобен от алгебричния (спойлер: не днес).

Определение. Нека точка $a$ е отбелязана на числовата ос. След това модулът $\left| x-a \right|$ е разстоянието от точка $x$ до точка $a$ на тази права.

Ако нарисувате картина, ще получите нещо подобно:

По един или друг начин, от дефиницията на модул веднага следва неговото ключово свойство: модулът на числото винаги е неотрицателна величина. Този факт ще бъде червена нишка през целия ни разказ днес.

Решаване на неравенства. Интервален метод

Сега нека да разгледаме неравенствата. Има много от тях, но нашата задача сега е да можем да решим поне най-простия от тях. Такива, които се свеждат до линейни неравенства, както и до интервалния метод.

Имам два големи урока по тази тема (между другото, много, МНОГО полезни - препоръчвам да ги изучавате):

1. Интервален метод за неравенства (особено гледайте видеото);
2. Дробните рационални неравенства са много обширен урок, но след него няма да имате абсолютно никакви въпроси.

Ако знаете всичко това, ако фразата „да преминем от неравенство към уравнение“ не ви кара да имате смътно желание да се ударите в стената, значи сте готови: добре дошли в ада в основната тема на урока. :)

1. Неравенства от формата „Модулът е по-малък от функцията“

Това е един от най-честите проблеми с модулите. Необходимо е да се реши неравенство от вида:

\[\ляво| f\надясно| \ltg\]

Функциите $f$ и $g$ могат да бъдат всякакви, но обикновено са полиноми. Примери за такива неравенства:

\[\begin(align) & \left| 2x+3 \надясно| \lt x+7; \\ & \left| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0; \\ & \left| ((x)^(2))-2\left| x \right|-3 \right| \lt 2. \\\край (подравняване)\]

Всички те могат да бъдат решени буквално в един ред по следната схема:

\[\ляво| f\надясно| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(align) & f \lt g, \\ & f \gt -g \\\end(align) \право.\право)\]

Лесно се вижда, че се отърваваме от модула, но в замяна получаваме двойно неравенство (или, което е същото, система от две неравенства). Но този преход отчита абсолютно всички възможни проблеми: ако числото под модула е положително, методът работи; ако е отрицателен, той все още работи; и дори с най-неадекватната функция на мястото на $f$ или $g$, методът пак ще работи.

Естествено възниква въпросът: не може ли да бъде по-просто? За съжаление не е възможно. Това е целият смисъл на модула.

Но стига с философстването. Нека разрешим няколко проблема:

Задача. Решете неравенството:

\[\ляво| 2x+3 \надясно| \lt x+7\]

Решение. И така, пред нас е класическо неравенство под формата „модулът е по-малък“ - дори няма какво да се трансформира. Ние работим по алгоритъма:

\[\begin(align) & \left| f\надясно| \lt g\Стрелка надясно -g \lt f \lt g; \\ & \left| 2x+3 \надясно| \lt x+7\Стрелка надясно -\left(x+7 \right) \lt 2x+3 \lt x+7 \\\end(align)\]

Не бързайте да отваряте скобите, предшествани от „минус“: напълно възможно е поради бързината да направите обидна грешка.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

Задачата се сведе до две елементарни неравенства. Нека отбележим техните решения на успоредни числови прави:

Пресечна точка на много

Пресечната точка на тези множества ще бъде отговорът.

Отговор: $x\in \left(-\frac(10)(3);4 \right)$

Задача. Решете неравенството:

\[\ляво| ((x)^(2))+2x-3 \right|+3\left(x+1 \right) \lt 0\]

Решение. Тази задача е малко по-трудна. Първо, нека изолираме модула, като преместим втория член надясно:

\[\ляво| ((x)^(2))+2x-3 \right| \lt -3\наляво(x+1 \надясно)\]

Очевидно отново имаме неравенство от формата „модулът е по-малък“, така че се отърваваме от модула, използвайки вече известния алгоритъм:

\[-\left(-3\left(x+1 \right) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

Сега внимание: някой ще каже, че съм малко перверзник с всички тези скоби. Но нека ви напомня още веднъж, че основната ни цел е решете правилно неравенството и получете отговора. По-късно, когато усвоите перфектно всичко, описано в този урок, можете сами да го изопачите, както желаете: отваряйте скоби, добавяйте минуси и т.н.

Като начало, просто ще се отървем от двойното минус вляво:

\[-\left(-3\left(x+1 \right) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\ляво(x+1 \дясно)\]

Сега нека отворим всички скоби в двойното неравенство:

Да преминем към двойното неравенство. Този път изчисленията ще бъдат по-сериозни:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(align) \right.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( подравняване)\надясно.\]

И двете неравенства са квадратни и могат да бъдат решени по интервалния метод (затова казвам: ако не знаете какво е това, по-добре все още да не се захващате с модули). Нека преминем към уравнението в първото неравенство:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \right)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\край (подравняване)\]

Както можете да видите, резултатът е непълно квадратно уравнение, което може да бъде решено по елементарен начин. Сега нека разгледаме второто неравенство на системата. Там ще трябва да приложите теоремата на Виета:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\край (подравняване)\]

Отбелязваме получените числа на две успоредни линии (отделно за първото неравенство и отделно за второто):

Отново, тъй като решаваме система от неравенства, ние се интересуваме от пресечната точка на защрихованите множества: $x\in \left(-5;-2 \right)$. Това е отговорът.

Отговор: $x\in \left(-5;-2 \right)$

Мисля, че след тези примери схемата на решение е пределно ясна:

1. Изолирайте модула, като преместите всички други членове в противоположната страна на неравенството. Така получаваме неравенство от вида $\left| f\надясно| \ltg$.
2. Решете това неравенство, като се отървете от модула според описаната по-горе схема. В един момент ще трябва да се преместите от двойно неравенствокъм система от два независими израза, всеки от които вече може да бъде решен отделно.
3. И накрая, всичко, което остава, е да пресечем решенията на тези два независими израза - и това е всичко, ще получим окончателния отговор.

Подобен алгоритъм съществува за неравенства от следния тип, когато модулът е по-голям от функцията. Има обаче няколко сериозни „но“. Сега ще говорим за тези „но“.

2. Неравенства от формата „Модулът е по-голям от функцията“

Те изглеждат така:

\[\ляво| f\надясно| \gtg\]

Подобен на предишния? Изглежда. И все пак такива проблеми се решават по съвсем различен начин. Формално схемата е следната:

\[\ляво| f\надясно| \gt g\Rightarrow \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(align) \right.\]

С други думи, разглеждаме два случая:

1. Първо, просто игнорираме модула и решаваме обичайното неравенство;
2. След това, по същество, разширяваме модула със знака минус и след това умножаваме двете страни на неравенството по −1, докато имам знака.

В този случай опциите се комбинират с квадратна скоба, т.е. Пред нас е комбинация от две изисквания.

Моля, обърнете внимание отново: следователно това не е система, а цялост в отговора множествата са комбинирани, а не пресичащи се. Това е фундаментална разлика от предишната точка!

Като цяло, много студенти са напълно объркани със съюзите и пресичанията, така че нека разрешим този проблем веднъж завинаги:

• "∪" е знак на съюза. По същество това е стилизирана буква "U", която дойде при нас на английскии е съкращение от „Съюз“, т.е. „Асоциации“.
• „∩“ е знакът за пресичане. Тези глупости не идват отникъде, а просто се появяват като контрапункт на „∪“.

За да бъде още по-лесно да запомните, просто нарисувайте крака към тези знаци, за да направите очила (само не ме обвинявайте сега, че насърчавам наркоманиите и алкохолизма: ако сериозно изучавате този урок, значи вече сте наркоман):

Преведено на руски това означава следното: съюзът (съвкупността) включва елементи от двете множества, следователно по никакъв начин не е по-малък от всеки от тях; но пресечната точка (системата) включва само тези елементи, които са едновременно както в първото множество, така и във второто. Следователно пресечната точка на множествата никога не е по-голяма от изходните множества.

Значи стана по-ясно? Това е страхотно. Да преминем към практиката.

Задача. Решете неравенството:

\[\ляво| 3x+1 \надясно| \gt 5-4x\]

Решение. Продължаваме по схемата:

\[\ляво| 3x+1 \надясно| \gt 5-4x\дясна стрелка \left[ \begin(align) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \right) \\\end(align) \ точно.\]

Решаваме всяко неравенство в популацията:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \right.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

Маркираме всеки получен набор на числовата линия и след това ги комбинираме:

Обединение на комплекти

Съвсем очевидно е, че отговорът ще бъде $x\in \left(\frac(4)(7);+\infty \right)$

Отговор: $x\in \left(\frac(4)(7);+\infty \right)$

Задача. Решете неравенството:

\[\ляво| ((x)^(2))+2x-3 \right| \gt x\]

Решение. Добре? Нищо - всичко е същото. Преминаваме от неравенство с модул към набор от две неравенства:

\[\ляво| ((x)^(2))+2x-3 \right| \gt x\Rightarrow \left[ \begin(align) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\end(align) \right.\]

Решаваме всяко неравенство. За съжаление, корените там няма да са много добри:

\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\&D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\край (подравняване)\]

Второто неравенство също е малко диво:

\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\&D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\край (подравняване)\]

Сега трябва да маркирате тези числа на две оси - по една ос за всяко неравенство. Трябва обаче да маркирате точките в правилния ред: отколкото по-голям брой, колкото повече изместваме точката надясно.

И тук ни очаква настройка. Ако всичко е ясно с числата $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (членовете в числителя на първия дроб са по-малки от членовете в числителя на втория, така че сумата също е по-малка), с числата $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ също няма да има затруднения (положителното число очевидно е по-отрицателно), тогава с последната двойка всичко не е толкова ясно. Кое е по-голямо: $\frac(-3+\sqrt(21))(2)$ или $\frac(-1+\sqrt(13))(2)$? Разположението на точките върху числовите оси и всъщност отговорът ще зависи от отговора на този въпрос.

Така че нека сравним:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrix)\]

Изолирахме корена, получихме неотрицателни числа от двете страни на неравенството, така че имаме право да поставим на квадрат и двете страни:

\[\begin(matrix) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \ 4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrix)\]

Мисля, че е безсмислено, че $4\sqrt(13) \gt 3$, така че $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, крайните точки на осите ще бъдат поставени така:

Случай на грозни корени

Нека ви напомня, че решаваме множество, така че отговорът ще бъде обединение, а не пресичане на защриховани множества.

Отговор: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty \right)$

Както можете да видите, нашата схема работи чудесно както за прости, така и за много трудни проблеми. Единственото „слабо място“ в този подход е, че трябва да сравнявате правилно ирационални числа(и повярвайте ми: не са само корените). Но отделен (и много сериозен) урок ще бъде посветен на проблемите на сравнението. И продължаваме напред.

3. Неравенства с неотрицателни „опашки“

Сега стигаме до най-интересната част. Това са неравенства от вида:

\[\ляво| f\надясно| \gt\наляво| g\надясно|\]

Най-общо казано, алгоритъмът, за който ще говорим сега, е правилен само за модула. Работи във всички неравенства, където има гарантирани неотрицателни изрази отляво и отдясно:

Какво да правим с тези задачи? Просто запомни:

В неравенства с неотрицателни „опашки“ и двете страни могат да бъдат повдигнати на всяка естествена степен. Няма да има допълнителни ограничения.

На първо място, ще се интересуваме от квадратурата - тя изгаря модули и корени:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\left(\sqrt(f) \right))^(2))=f. \\\край (подравняване)\]

Просто не бъркайте това с вземане на корен от квадрат:

\[\sqrt(((f)^(2)))=\left| f \right|\ne f\]

Безброй грешки бяха направени, когато ученик забрави да инсталира модул! Но това е съвсем различна история (това са, така да се каже, ирационални уравнения), така че няма да навлизаме в това сега. Нека решим по-добре няколко проблема:

Задача. Решете неравенството:

\[\ляво| x+2 \right|\ge \left| 1-2x \right|\]

Решение. Нека веднага да отбележим две неща:

1. Това не е строго неравенство. Точките на числовата ос ще бъдат пробити.
2. И двете страни на неравенството очевидно са неотрицателни (това е свойство на модула: $\left| f\left(x \right) \right|\ge 0$).

Следователно можем да повдигнем на квадрат двете страни на неравенството, за да се отървем от модула и да решим проблема, използвайки обичайния метод на интервала:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\left(x+2 \right))^(2))\ge ((\left(2x-1 \right))^(2)). \\\край (подравняване)\]

На последната стъпка изневерих малко: промених последователността от членове, като се възползвах от четността на модула (всъщност умножих израза $1-2x$ по −1).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ дясно)\дясно)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \right)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

Решаваме с помощта на интервалния метод. Нека преминем от неравенство към уравнение:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\край (подравняване)\]

Отбелязваме намерените корени на числовата ос. Още веднъж: всички точки са защриховани, защото първоначалното неравенство не е строго!

Отървете се от знака за модул

Нека напомня за тези, които са особено упорити: вземаме знаците от последното неравенство, което беше написано преди да преминем към уравнението. И рисуваме върху площите, изисквани в същото неравенство. В нашия случай това е $\left(x-3 \right)\left(3x+1 \right)\le 0$.

Добре, всичко свърши. Проблемът е решен.

Отговор: $x\in \left[ -\frac(1)(3);3 \right]$.

Задача. Решете неравенството:

\[\ляво| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \right|\]

Решение. Правим всичко по същия начин. Няма да коментирам - просто вижте последователността на действията.

Квадратирайте го:

\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \right| \right))^(2))\le ((\left(\left | ((x)^(2))+3x+4 \right| \right))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))\le ((\left(((x)^(2))+3x+4 \десен))^(2)); \\ & ((\left(((x)^(2))+x+1 \right))^(2))-((\left(((x)^(2))+3x+4 \ надясно))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \right)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

Интервален метод:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Стрелка надясно x=-1.5; \\ & 2((x)^(2))+4x+5=0\Стрелка надясно D=16-40 \lt 0\Стрелка надясно \varnothing . \\\край (подравняване)\]

На числовата ос има само един корен:

Отговорът е цял интервал

Отговор: $x\in \left[ -1.5;+\infty \right)$.

Малка забележка за последната задача. Както един от моите ученици точно отбеляза, и двата подмодулни израза в това неравенство са очевидно положителни, така че знакът за модул може да бъде пропуснат без вреда за здравето.

Но това е съвсем друго ниво на мислене и друг подход – условно може да се нарече метод на следствията. За това - в отделен урок. Сега нека преминем към последната част от днешния урок и да разгледаме един универсален алгоритъм, който винаги работи. Дори когато всички предишни подходи бяха безсилни. :)

4. Метод на изброяване на опциите

Ами ако всички тези техники не помогнат? Ако неравенството не може да бъде сведено до неотрицателни опашки, ако е невъзможно да се изолира модулът, ако като цяло има болка, тъга, меланхолия?

Тогава на сцената излиза „тежката артилерия“ на цялата математика – методът на грубата сила. Във връзка с неравенства с модул изглежда така:

1. Изпишете всички подмодулни изрази и ги задайте равни на нула;
2. Решете получените уравнения и маркирайте намерените корени на една числова ос;
3. Правата линия ще бъде разделена на няколко секции, в рамките на които всеки модул има фиксиран знак и следователно се разкрива уникално;
4. Решете неравенството на всеки такъв участък (можете отделно да разгледате корените-граници, получени в стъпка 2 - за надеждност). Комбинирайте резултатите - това ще бъде отговорът. :)

И как? слаб? Лесно! Само за дълго време. Да видим на практика:

Задача. Решете неравенството:

\[\ляво| x+2 \надясно| \lt \наляво| x-1 \right|+x-\frac(3)(2)\]

Решение. Тези глупости не се свеждат до неравенства като $\left| f\надясно| \lt g$, $\left| f\надясно| \gt g$ или $\left| f\надясно| \lt \наляво| g \right|$, така че действаме напред.

Изписваме подмодулни изрази, приравняваме ги към нула и намираме корените:

\[\begin(align) & x+2=0\Rightarrow x=-2; \\ & x-1=0\Стрелка надясно x=1. \\\край (подравняване)\]

Общо имаме два корена, които разделят числовата линия на три секции, в които всеки модул се разкрива уникално:

Разделяне на числовата ос с нули на подмодулни функции

Нека разгледаме всеки раздел поотделно.

1. Нека $x \lt -2$. Тогава и двата подмодулни израза са отрицателни и първоначалното неравенство ще бъде пренаписано, както следва:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1.5 \\ & -x-2 \lt -x+1+ x- 1.5 \\ & x \gt 1.5 \\\end(align)\]

Имаме доста просто ограничение. Нека го пресечем с първоначалното предположение, че $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1.5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Очевидно променливата $x$ не може едновременно да бъде по-малка от −2 и по-голяма от 1,5. В тази област няма решения.

1.1. Нека разгледаме отделно граничния случай: $x=-2$. Нека просто заместим това число в първоначалното неравенство и да проверим: вярно ли е?

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=-2) ) \ \ & 0 \lt \left| -3\дясно|-2-1,5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0.5\Стрелка надясно \varnothing . \\\край (подравняване)\]

Очевидно е, че веригата от изчисления ни е довела до неправилно неравенство. Следователно първоначалното неравенство също е невярно и $x=-2$ не е включено в отговора.

2. Нека сега $-2 \lt x \lt 1$. Левият модул вече ще се отвори с „плюс“, но десният все още ще се отвори с „минус“. Ние имаме:

\[\begin(align) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\край (подравняване)\]

Отново се пресичаме с първоначалното изискване:

\[\left\( \begin(align) & x \lt -2.5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

И отново, множеството от решения е празно, тъй като няма числа, които да са едновременно по-малки от −2,5 и по-големи от −2.

2.1. И отново специален случай: $x=1$. Заменяме в първоначалното неравенство:

\[\begin(align) & ((\left. \left| x+2 \right| \lt \left| x-1 \right|+x-1,5 \right|)_(x=1)) \\ & \ляво| 3\надясно| \lt \наляво| 0\дясно|+1-1,5; \\ & 3 \lt -0,5; \\ & 3 \lt -0.5\Стрелка надясно \varnothing . \\\край (подравняване)\]

Подобно на предишния „специален случай“, числото $x=1$ очевидно не е включено в отговора.

3. Последната част от реда: $x \gt 1$. Тук всички модули се отварят със знак плюс:

\[\begin(align) & x+2 \lt x-1+x-1.5 \\ & x+2 \lt x-1+x-1.5 \\ & x \gt 4.5 \\ \end(align)\ ]

И отново пресичаме намереното множество с оригиналното ограничение:

\[\left\( \begin(align) & x \gt 4.5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4.5;+\infty \right)\ ]

Най-накрая! Намерихме интервал, който ще бъде отговорът.

Отговор: $x\in \left(4,5;+\infty \right)$

И накрая, една бележка, която може да ви спаси от глупави грешкипри решаване на реални проблеми:

Решенията на неравенства с модули обикновено представляват непрекъснати множества на числовата ос - интервали и отсечки. Изолираните точки са много по-рядко срещани. И още по-рядко се случва границата на решението (края на сегмента) да съвпада с границата на разглеждания диапазон.

Следователно, ако границите (същите „специални случаи“) не са включени в отговора, тогава областите отляво и отдясно на тези граници почти сигурно няма да бъдат включени в отговора. И обратното: границата, въведена в отговора, което означава, че някои области около нея също ще бъдат отговори.

Имайте това предвид, когато преглеждате вашите решения.