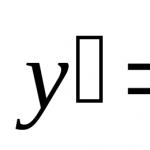И така, имаме степени на две. Ако вземете числото от долния ред, можете лесно да намерите степента, до която ще трябва да повишите две, за да получите това число. Например, за да получите 16, трябва да повдигнете две на четвърта степен. И за да получите 64, трябва да повдигнете две на шеста степен. Това се вижда от таблицата.
А сега всъщност дефиницията на логаритъма:
Логаритъмът с основа a от x е степента, на която a трябва да се повдигне, за да се получи x.
Нотация: log a x = b, където a е основата, x е аргументът, b е това, на което всъщност е равен логаритъма.
Например 2 3 = 8 ⇒ log 2 8 = 3 (логаритъмът с основа 2 на 8 е три, защото 2 3 = 8). Със същия успех, регистрирайте 2 64 = 6, тъй като 2 6 = 64.
Операцията за намиране на логаритъм на число по дадена основа се нарича логаритмиране. И така, нека добавим нов ред към нашата таблица:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
За съжаление, не всички логаритми се изчисляват толкова лесно. Например, опитайте се да намерите log 2 5. Числото 5 не е в таблицата, но логиката диктува, че логаритъма ще лежи някъде в интервала. Защото 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Такива числа се наричат ирационални: числата след десетичната запетая могат да се записват безкрайно и никога не се повтарят. Ако логаритъмът се окаже ирационален, по-добре е да го оставите така: log 2 5, log 3 8, log 5 100.
Важно е да се разбере, че логаритъмът е израз с две променливи (основа и аргумент). Много хора в началото бъркат къде е основата и къде аргументът. Да избегна досадни недоразумения, просто погледнете снимката:
[Надпис към снимката]
Пред нас не е нищо повече от определението на логаритъм. Помня: логаритъмът е степен, в който трябва да бъде вградена базата, за да се получи аргумент. Това е основата, която се повдига на степен - тя е подчертана в червено на снимката. Оказва се, че основата винаги е на дъното! Казвам на учениците си това прекрасно правило още на първия урок - и не възниква объркване.
Разбрахме определението - остава само да се научим да броим логаритми, т.е. отървете се от знака "дневник". Като начало отбелязваме, че от определението следват два важни факта:
- Аргументът и основата винаги трябва да са по-големи от нула. Това следва от определението за степен рационален показател, до което се свежда определението за логаритъм.
- Базата трябва да е различна от едно, тъй като едното във всяка степен си остава едно. Поради това въпросът „до каква сила трябва да бъде издигнат, за да получи две“ е безсмислен. Няма такава степен!
Такива ограничения се наричат диапазон от приемливи стойности(ODZ). Оказва се, че ODZ на логаритъма изглежда така: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Имайте предвид, че няма ограничения за числото b (стойността на логаритъма). Например логаритъма може да е отрицателен: log 2 0,5 = −1, защото 0,5 = 2 −1.
Сега обаче само обмисляме числови изрази, където не се изисква да се знае CVD на логаритъма. Всички ограничения вече са взети предвид от авторите на проблемите. Но когато си отидат логаритмични уравненияи неравенства, изискванията на DHS ще станат задължителни. В крайна сметка основата и аргументът може да съдържат много силни конструкции, които не отговарят непременно на горните ограничения.
Сега нека да разгледаме общата схема за изчисляване на логаритми. Състои се от три стъпки:
- Изразете основата a и аргумента x като степен с минималната възможна основа, по-голяма от едно. По пътя е по-добре да се отървете от десетичните знаци;
- Решете уравнението за променлива b: x = a b ;
- Полученото число b ще бъде отговорът.
Това е всичко! Ако логаритъмът се окаже ирационален, това ще се види още в първата стъпка. Изискването базата да е по-голяма от единица е много важно: това намалява вероятността от грешка и значително опростява изчисленията. Същото е и с десетичните дроби: ако веднага ги преобразувате в обикновени, ще има много по-малко грешки.
Нека видим как работи тази схема, използвайки конкретни примери:
Задача. Изчислете логаритъма: log 5 25
- Нека си представим основата и аргумента като степен на пет: 5 = 5 1 ; 25 = 5 2 ;
- Нека съставим и решим уравнението:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2; - Получихме отговор: 2.
Задача. Изчислете логаритъма:
[Надпис към снимката]
Задача. Изчислете логаритъма: log 4 64
- Нека си представим основата и аргумента като степен на две: 4 = 2 2 ; 64 = 2 6 ;
- Нека съставим и решим уравнението:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3; - Получихме отговор: 3.
Задача. Изчислете логаритъма: log 16 1
- Нека си представим основата и аргумента като степен на две: 16 = 2 4 ; 1 = 20;
- Нека съставим и решим уравнението:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0; - Получихме отговор: 0.
Задача. Изчислете логаритъма: log 7 14
- Нека си представим основата и аргумента като степен на седем: 7 = 7 1 ; 14 не може да бъде представено като степен на седем, тъй като 7 1< 14 < 7 2 ;
- От предходния параграф следва, че логаритъма не се брои;
- Отговорът е без промяна: log 7 14.
Малка забележка към последния пример. Как можете да сте сигурни, че едно число не е точна степен на друго число? Много е просто - просто го разбийте на основни фактори. И ако такива множители не могат да бъдат събрани в степени с еднакви показатели, тогава оригиналното число не е точна степен.
Задача. Разберете дали числата са точни степени: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 - точна степен, т.к има само един множител;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - не е точна степен, тъй като има два фактора: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - точна степен;
35 = 7 · 5 - отново не е точна степен;
14 = 7 · 2 - отново не е точна степен;
Нека отбележим също, че самите ние прости числавинаги са точни степени на себе си.
Десетичен логаритъм
Някои логаритми са толкова често срещани, че имат специално име и символ.
Десетичният логаритъм от x е логаритъмът при основа 10, т.е. Степента, на която трябва да се повдигне числото 10, за да се получи числото x. Обозначение: lg x.
Например, log 10 = 1; log 100 = 2; lg 1000 = 3 - и т.н.
Отсега нататък, когато в учебника се появи фраза като „Намерете lg 0.01“, знайте, че това не е печатна грешка. Това е десетичен логаритъм. Ако обаче не сте запознати с тази нотация, винаги можете да я пренапишете:
log x = log 10 x
Всичко, което е вярно за обикновените логаритми, е вярно и за десетичните логаритми.
Натурален логаритъм
Има друг логаритъм, който има свое собствено обозначение. В някои отношения това е дори по-важно от десетичната запетая. Това е заотносно натуралния логаритъм.
Натуралният логаритъм от x е логаритъмът по основа e, т.е. степента, на която трябва да се повдигне числото e, за да се получи числото x. Обозначение: ln x .
Мнозина ще попитат: какво е числото e? Това е ирационално число, точната му стойност не може да бъде намерена и записана. Ще дам само първите цифри:
e = 2,718281828459...
Няма да навлизаме в подробности какво представлява този номер и защо е необходим. Само не забравяйте, че e е основата на естествения логаритъм:
ln x = log e x
Така ln e = 1; ln e 2 = 2; ln e 16 = 16 - и т.н. От друга страна, ln 2 е ирационално число. Като цяло, естественият логаритъм на който и да е рационално числоирационален. С изключение, разбира се, на едно: ln 1 = 0.
За естествените логаритми са валидни всички правила, които са валидни за обикновените логаритми.
ОПРЕДЕЛЕНИЕ
Десетичен логаритъмнаречен логаритъм с основа 10:
Title="Изобразено от QuickLaTeX.com">!}
Този логаритъм е решението експоненциално уравнение. Понякога (особено в чужда литература) десетичният логаритъм също се означава като , въпреки че първите две обозначения също са присъщи на натуралния логаритъм.
Първите таблици с десетични логаритми са публикувани от английския математик Хенри Бригс (1561-1630) през 1617 г. (затова чуждестранните учени често наричат десетичните логаритми също Бригс), но тези таблици съдържат грешки. Въз основа на таблиците (1783) на словенския и австрийския математик Георг Барталомей Вега (Юри Веха или Веховец, 1754-1802), през 1857 г. немският астроном и геодезист Карл Бремикер (1804-1877) публикува първото издание без грешки. С участието на руския математик и учител Леонтий Филипович Магнитски (Телятин или Теляшин, 1669-1739) през 1703 г. в Русия са публикувани първите логаритмични таблици. Десетичните логаритми бяха широко използвани за изчисления.
Свойства на десетичните логаритми
Този логаритъм има всички свойства, присъщи на логаритъм към произволна основа:
1. Основна логаритмична идентичност:
5. ![]() .
.
7. Преход към нова база:
![]()
Функцията десетичен логаритъм е функция. Графиката на тази крива често се нарича логаритмичен.
Свойства на функцията y=lg x
1) Обхват на дефиницията: .
2) Множество значения: .
3) Обща функция.
4) Функцията е непериодична.
5) Графиката на функцията пресича оста x в точка .
6) Интервали на постоянство на знака: title="Rendered by QuickLaTeX.com" height="16" width="44" style="vertical-align: -4px;"> для !} ![]() че за .
че за .
Те често вземат числото десет. Наричат се логаритми на числа, базирани на основа десет десетичен знак. Когато извършвате изчисления с десетичен логаритъм, обичайно е да работите със знака lg, но не дневник; в този случай числото десет, което определя основата, не е посочено. Да, да заменим дневник 10 105до опростено lg105; А дневник 10 2На lg2.
За десетични логаритмитипични са същите характеристики, които имат логаритмите с основа, по-голяма от единица. А именно десетичните логаритми се характеризират изключително за положителни числа. Десетичните логаритми на числа, по-големи от едно, са положителни, а тези на числа, по-малки от едно, са отрицателни; от две неотрицателни числа, по-голямото е еквивалентно на по-големия десетичен логаритъм и т.н. Освен това десетичните логаритми имат отличителни чертии специфични характеристики, които обясняват защо е удобно да се предпочита числото десет като основа на логаритмите.
Преди да разгледаме тези свойства, нека се запознаем със следните формулировки.
Цяла част от десетичния логаритъм на число Ае наречен Характеристика, а дробната е мантисатози логаритъм.
Характеристики на десетичен логаритъм на число Асе обозначава като , а мантисата като (lg А}.
Да вземем, да речем, log 2 ≈ 0,3010.Съответно = 0, (log 2) ≈ 0,3010.
По същия начин за log 543.1 ≈2.7349. Съответно, = 2, (log 543.1)≈ 0.7349.
Изчисляването на десетични логаритми на положителни числа от таблици се използва широко.
Характеристики на десетичните логаритми.
Първият знак на десетичния логаритъм.цялотоНе отрицателно число, представено от единица, последвана от нули, е цялоположително число, равно на броя нули в избраното число .
Нека вземем log 100 = 2, log 1 00000 = 5.
Най-общо казано, ако
Че А= 10н , от които получаваме
lg a = lg 10 n = n lg 10 =П.
Втори знак.Десетичен логаритъм от положителен десетичен знак дроби, показано като единица с водещи нули, е - П, Където П- броят на нулите в представянето на това число, като се вземат предвид нула цели числа.
Нека помислим , log 0,001 = - 3, log 0,000001 = -6.
Най-общо казано, ако
,
Че а= 10-н и се оказва
lga= lg 10н =-n log 10 =-n
Трети знак.Характеристики на десетичната система логаритъмнеотрицателно число, по-голямо от едно, е равно на броя на цифрите в цялата част на това число без единица.
Нека анализираме тази характеристика: 1) Характеристиката на логаритъма lg 75.631 е равна на 1.
Наистина, 10< 75,631 < 100. Из этого можно сделать вывод
lg 10< lg 75,631 < lg 100,
1 < lg 75,631 < 2.
Това предполага,
log 75.631 = 1 +b,
Отместване на запетая десетичен знакдясно или ляво е еквивалентно на операцията умножениетази дроб на степен десет с цяло число П(положителен или отрицателен). И следователно, когато десетичната запетая в положителна десетична дроб се измести наляво или надясно, мантисата на десетичния логаритъм на тази дроб не се променя.
И така, (log 0,0053) = (log 0,53) = (log 0,0000053).