ЗАДАЧИ С2 ОТ ЕДИНИЯ ДЪРЖАВЕН ИЗПИТ ПО МАТЕМАТИКА ЗА НАМИРАНЕ НА РАЗСТОЯНИЕТО ОТ ТОЧКА ДО РАВНИНА
Куликова Анастасия Юриевна
5-ти курс, катедра Мат. анализ, алгебра и геометрия EI KFU, Руска Федерация, Република Татарстан, Елабуга
Ганеева Айгул Рифовна
научен ръководител д.ф.н. пед. Науки, доцент EI KFU, Руска Федерация, Република Татарстан, Елабуга
През последните години в задачите на Единния държавен изпит по математика се появиха задачи за изчисляване на разстоянието от точка до равнина. В тази статия, използвайки примера на една задача, се разглеждат различни методи за намиране на разстоянието от точка до равнина. Най-подходящият метод може да се използва за решаване на различни проблеми. След като решите проблем с един метод, можете да проверите правилността на резултата с друг метод.
Определение.Разстоянието от точка до равнина, която не съдържа тази точка, е дължината на перпендикуляра, прекаран от тази точка към дадената равнина.
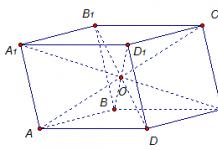
Задача.Даден е правоъгълен паралелепипед АбСЪСД.А. 1 б 1 ° С 1 д 1 със страни AB=2, пр.н.е.=4, А.А. 1 =6. Намерете разстоянието от точката дда рендосвам ACд 1 .
1 начин. Използвайки определение. Намерете разстоянието r( д, ACд 1) от точка дда рендосвам ACд 1 (фиг. 1).
Фигура 1. Първи метод
Нека изпълним Д.Х.⊥AC, следователно, по теоремата за три перпендикуляра д 1 з⊥ACИ (DD 1 з)⊥AC. Нека изпълним директен Д.Т.перпендикулярен д 1 з. Направо Д.Т.лежи в равнина DD 1 з, следователно Д.Т.⊥A.C.. следователно Д.Т.⊥ACд 1.
АDCнека намерим хипотенузата ACи височина Д.Х.
![]()
От правоъгълен триъгълник д 1 Д.Х. нека намерим хипотенузата д 1 зи височина Д.Т.
![]()

Отговор: .
Метод 2.Обемен метод (използване на спомагателна пирамида). Задача от този тип може да се сведе до задачата за изчисляване на височината на пирамида, където височината на пирамидата е необходимото разстояние от точка до равнина. Докажете, че тази височина е търсеното разстояние; намерете обема на тази пирамида по два начина и изразете тази височина.
Обърнете внимание, че с този метод не е необходимо да се конструира перпендикуляр от дадена точка към дадена равнина.
Кубоидът е паралелепипед, чиито лица са правоъгълници.
AB=CD=2, пр.н.е.=AD=4, А.А. 1 =6.
Необходимото разстояние ще бъде височината чпирамиди ACD 1 д, спуснат отгоре двърху основата ACD 1 (фиг. 2).
Нека изчислим обема на пирамидата ACD 1 ддва начина.
При пресмятането по първия начин вземаме ∆ за основа ACD 1 тогава
![]()
При изчисляване по втория начин вземаме ∆ за основа ACD, Тогава
![]()
Нека приравним десните части на последните две равенства и получим
![]()
![]()

Фигура 2. Втори метод
От правоъгълни триъгълници ACд, ДОБАВЯНЕ 1 , CDD 1 намерете хипотенузата с помощта на Питагоровата теорема
ACD
![]()
Изчислете площта на триъгълника ACд 1, използвайки формулата на Heron
![]()
Отговор: .
3 начина. Координатен метод.
Нека се даде точка М(х 0 ,г 0 ,z 0) и равнина α , дадено от уравнението брадва+от+cz+д=0 в правоъгълна декартова координатна система. Разстояние от точката Мкъм равнината α може да се изчисли по формулата:

Да въведем координатна система (фиг. 3). Начало на координатите в точка IN;
Направо AB- ос х, направо слънце- ос г, направо BB 1 - ос z.

Фигура 3. Трети метод
б(0,0,0), А(2,0,0), СЪС(0,4,0), д(2,4,0), д 1 (2,4,6).
Позволявам аx+от+ cz+ д=0 – уравнение на равнина ACD 1 . Заместване на координатите на точки в него А, ° С, д 1 получаваме:

![]()
Уравнение на равнината ACD 1 ще приеме формата
Отговор: .
4 начин. Векторен метод.
Нека въведем основата (фиг. 4) , .

Фигура 4. Четвърти метод
Поддържането на вашата поверителност е важно за нас. Поради тази причина разработихме Политика за поверителност, която описва как използваме и съхраняваме вашата информация. Моля, прегледайте нашите практики за поверителност и ни уведомете, ако имате въпроси.
Събиране и използване на лична информация
Личната информация се отнася до данни, които могат да бъдат използвани за идентифициране или контакт с конкретно лице.
Може да бъдете помолени да предоставите вашата лична информация по всяко време, когато се свържете с нас.
По-долу са дадени някои примери за видовете лична информация, която можем да събираме и как можем да използваме тази информация.
Каква лична информация събираме:
- Когато подадете заявление на сайта, може да съберем различна информация, включително вашето име, телефонен номер, имейл адрес и др.
Как използваме вашата лична информация:
- Личната информация, която събираме, ни позволява да се свържем с вас с уникални оферти, промоции и други събития и предстоящи събития.
- От време на време може да използваме вашата лична информация, за да изпращаме важни известия и съобщения.
- Може също така да използваме лична информация за вътрешни цели, като например извършване на одити, анализ на данни и различни изследвания, за да подобрим услугите, които предоставяме, и да ви предоставим препоръки относно нашите услуги.
- Ако участвате в теглене на награди, конкурс или подобна промоция, ние може да използваме предоставената от вас информация за администриране на такива програми.
Разкриване на информация на трети лица
Ние не разкриваме информацията, получена от вас, на трети страни.
Изключения:
- Ако е необходимо - в съответствие със закона, съдебна процедура, в съдебно производство и/или въз основа на публични искания или искания от държавни органи в Руската федерация - да разкриете вашата лична информация. Може също така да разкрием информация за вас, ако преценим, че такова разкриване е необходимо или подходящо за целите на сигурността, правоприлагането или други обществено значими цели.
- В случай на реорганизация, сливане или продажба, можем да прехвърлим личната информация, която събираме, на съответната трета страна приемник.
Защита на личната информация
Ние вземаме предпазни мерки – включително административни, технически и физически – за да защитим вашата лична информация от загуба, кражба и злоупотреба, както и неоторизиран достъп, разкриване, промяна и унищожаване.
Зачитане на вашата поверителност на фирмено ниво
За да гарантираме, че вашата лична информация е защитена, ние съобщаваме стандартите за поверителност и сигурност на нашите служители и стриктно прилагаме практиките за поверителност.
Тази статия говори за определяне на разстоянието от точка до равнина. Нека го анализираме с помощта на координатния метод, който ще ни позволи да намерим разстоянието от дадена точка в триизмерното пространство. За да затвърдим това, нека разгледаме примери за няколко задачи.
Разстоянието от точка до равнина се намира по известното разстояние от точка до точка, като едното от тях е дадено, а другото е проекция върху дадена равнина.
Когато в пространството е определена точка M 1 с равнина χ, тогава през точката може да се начертае права линия, перпендикулярна на равнината. H 1 е тяхната обща пресечна точка. От това получаваме, че отсечката M 1 H 1 е перпендикуляр, прекаран от точка M 1 към равнината χ, където точката H 1 е основата на перпендикуляра.
Определение 1
Разстоянието от дадена точка до основата на перпендикуляр, прекаран от дадена точка към дадена равнина, се нарича.
Дефиницията може да бъде написана в различни формулировки.
Определение 2
Разстояние от точка до равнинае дължината на перпендикуляра, прекаран от дадена точка към дадена равнина.
Разстоянието от точка M 1 до равнината χ се определя, както следва: разстоянието от точка M 1 до равнината χ ще бъде най-малкото от дадена точка до всяка точка на равнината. Ако точката H 2 се намира в равнината χ и не е равна на точката H 2, тогава получаваме правоъгълен триъгълник под формата M 2 H 1 H 2 , който е правоъгълен, където има крак M 2 H 1, M 2 H 2 – хипотенуза. Това означава, че следва, че M 1 H 1< M 1 H 2 . Тогда отрезок М 2 H 1 се счита за наклонена, която се изтегля от точка M 1 към равнината χ. Имаме, че перпендикулярът, прекаран от дадена точка към равнината, е по-малък от наклонения, прекаран от точката към дадената равнина. Нека разгледаме този случай на фигурата по-долу.

Разстояние от точка до равнина - теория, примери, решения
Има редица геометрични задачи, чиито решения трябва да съдържат разстоянието от точка до равнина. Може да има различни начини да се идентифицира това. За да разрешите, използвайте Питагоровата теорема или подобието на триъгълници. Когато според условието е необходимо да се изчисли разстоянието от точка до равнина, дадена в правоъгълна координатна система на тримерното пространство, то се решава по координатния метод. Този параграф обсъжда този метод.
Съгласно условията на задачата имаме, че е дадена точка в триизмерното пространство с координати M 1 (x 1, y 1, z 1) с равнина χ; необходимо е да се определи разстоянието от M 1 до равнината χ. Използват се няколко метода за решаване на този проблем.
Първи начин
Този метод се основава на намиране на разстоянието от точка до равнина с помощта на координатите на точка H 1, които са основата на перпендикуляра от точка M 1 към равнината χ. След това трябва да изчислите разстоянието между M 1 и H 1.
За да решите задачата по втория начин, използвайте нормалното уравнение на дадена равнина.
Втори начин
По условие имаме, че H 1 е основата на перпендикуляра, който е спуснат от точка M 1 към равнината χ. След това определяме координатите (x 2, y 2, z 2) на точка H 1. Необходимото разстояние от M 1 до равнината χ се намира по формулата M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2, където M 1 (x 1, y 1, z 1) и H 1 (x 2, y 2, z 2). За да решите, трябва да знаете координатите на точка H 1.
Имаме, че H 1 е пресечната точка на равнината χ с правата a, която минава през точката M 1, разположена перпендикулярно на равнината χ. От това следва, че е необходимо да се състави уравнение за права, минаваща през дадена точка, перпендикулярна на дадена равнина. Тогава ще можем да определим координатите на точка H 1. Необходимо е да се изчислят координатите на пресечната точка на правата и равнината.
Алгоритъм за намиране на разстоянието от точка с координати M 1 (x 1, y 1, z 1) до равнината χ:
Определение 3
- съставете уравнение на права линия a, минаваща през точка M 1 и в същото време
- перпендикулярна на равнината χ;
- намерете и изчислете координатите (x 2 , y 2 , z 2) на точка H 1, които са точки
- пресичане на права a с равнина χ;
- изчислете разстоянието от M 1 до χ, като използвате формулата M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + z 2 - z 1 2.
Трети начин
В дадена правоъгълна координатна система O x y z има равнина χ, тогава получаваме нормално уравнение на равнината под формата cos α · x + cos β · y + cos γ · z - p = 0. От тук получаваме, че разстоянието M 1 H 1 с точката M 1 (x 1 , y 1 , z 1), начертано към равнината χ, изчислено по формулата M 1 H 1 = cos α x + cos β y + cos γ z - p . Тази формула е валидна, тъй като е установена благодарение на теоремата.
Теорема
Ако точка M 1 (x 1, y 1, z 1) е дадена в триизмерно пространство, имаща нормално уравнение на равнината χ под формата cos α x + cos β y + cos γ z - p = 0, след това изчисляването на разстоянието от точката до равнината M 1 H 1 се получава от формулата M 1 H 1 = cos α · x + cos β · y + cos γ · z - p, тъй като x = x 1, y = y 1 , z = z 1.
Доказателство
Доказателството на теоремата се свежда до намиране на разстоянието от точка до права. От това получаваме, че разстоянието от M 1 до равнината χ е модулът на разликата между числената проекция на радиус-вектора M 1 с разстоянието от началото до равнината χ. Тогава получаваме израза M 1 H 1 = n p n → O M → - p. Нормалният вектор на равнината χ има формата n → = cos α, cos β, cos γ и дължината му е равна на единица, n p n → O M → е числената проекция на вектора O M → = (x 1, y 1 , z 1) в посоката, определена от вектора n → .
Нека приложим формулата за изчисляване на скаларни вектори. Тогава получаваме израз за намиране на вектор от вида n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → , тъй като n → = cos α , cos β , cos γ · z и O M → = (x 1 , y 1 , z 1) . Координатната форма на запис ще приеме формата n → , O M → = cos α · x 1 + cos β · y 1 + cos γ · z 1 , тогава M 1 H 1 = n p n → O M → - p = cos α · x 1 + cos β · y 1 + cos γ · z 1 - p . Теоремата е доказана.
От тук получаваме, че разстоянието от точката M 1 (x 1, y 1, z 1) до равнината χ се изчислява чрез заместване на cos α · x + cos β · y + cos γ · z - p = 0 в лявата страна на нормалното уравнение на равнината вместо x, y, z координати x 1, y 1 и z 1, отнасящи се до точка М 1, като се вземе абсолютната стойност на получената стойност.
Нека разгледаме примери за намиране на разстоянието от точка с координати до дадена равнина.
Пример 1
Изчислете разстоянието от точката с координати M 1 (5, - 3, 10) до равнината 2 x - y + 5 z - 3 = 0.
Решение
Нека решим проблема по два начина.
Първият метод започва с изчисляване на вектора на посоката на линията a. По условие имаме, че даденото уравнение 2 x - y + 5 z - 3 = 0 е общо уравнение на равнината, а n → = (2, - 1, 5) е нормалният вектор на дадената равнина. Използва се като насочващ вектор на права a, която е перпендикулярна на дадена равнина. Необходимо е да се запише каноничното уравнение на линия в пространството, минаваща през M 1 (5, - 3, 10) с насочващ вектор с координати 2, - 1, 5.
Уравнението ще се превърне в x - 5 2 = y - (- 3) - 1 = z - 10 5 ⇔ x - 5 2 = y + 3 - 1 = z - 10 5.
Трябва да се определят пресечните точки. За да направите това, внимателно комбинирайте уравненията в система, за да преминете от каноничните към уравненията на две пресичащи се линии. Нека вземем тази точка като H 1. Разбираме това
x - 5 2 = y + 3 - 1 = z - 10 5 ⇔ - 1 · (x - 5) = 2 · (y + 3) 5 · (x - 5) = 2 · (z - 10) 5 · ( y + 3) = - 1 · (z - 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0
След което трябва да активирате системата
x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 ⇔ x + 2 y = 1 5 x - 2 z = 5 2 x - y + 5 z = 3
Нека се обърнем към правилото за системно решение на Гаус:
1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0, y = - 1 10 10 + 2 z = - 1, x = - 1 - 2 y = 1
Получаваме, че H 1 (1, - 1, 0).
Изчисляваме разстоянието от дадена точка до равнината. Взимаме точки M 1 (5, - 3, 10) и H 1 (1, - 1, 0) и получаваме
M 1 H 1 = (1 - 5) 2 + (- 1 - (- 3)) 2 + (0 - 10) 2 = 2 30
Второто решение е първо да приведем даденото уравнение 2 x - y + 5 z - 3 = 0 в нормална форма. Определяме нормализиращия коефициент и получаваме 1 2 2 + (- 1) 2 + 5 2 = 1 30. Оттук извеждаме уравнението на равнината 2 30 · x - 1 30 · y + 5 30 · z - 3 30 = 0. Лявата страна на уравнението се изчислява чрез заместване на x = 5, y = - 3, z = 10 и трябва да вземете разстоянието от M 1 (5, - 3, 10) до 2 x - y + 5 z - 3 = 0 по модул. Получаваме израза:
M 1 H 1 = 2 30 5 - 1 30 - 3 + 5 30 10 - 3 30 = 60 30 = 2 30
Отговор: 2 30.
Когато равнината χ е зададена чрез един от методите в раздела за методи за определяне на равнина, тогава първо трябва да получите уравнението на равнината χ и да изчислите необходимото разстояние, като използвате произволен метод.
Пример 2
В тримерното пространство се задават точки с координати M 1 (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, - 1). Изчислете разстоянието от M 1 до равнината A B C.
Решение
Първо трябва да напишете уравнението на равнината, минаваща през дадените три точки с координати M 1 (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C ( 4, 0, - 1) .
x - 0 y - 2 z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 = 0 ⇔ x y - 2 z - 1 2 4 0 4 - 2 - 2 = 0 ⇔ ⇔ - 8 x + 4 y - 20 z + 12 = 0 ⇔ 2 x - y + 5 z - 3 = 0
От това следва, че задачата има решение, подобно на предишната. Това означава, че разстоянието от точка M 1 до равнината A B C има стойност 2 30.
Отговор: 2 30.
Намирането на разстоянието от дадена точка на равнина или до равнина, на която те са успоредни, е по-удобно чрез прилагане на формулата M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 - p . От това получаваме, че нормалните уравнения на равнините се получават в няколко стъпки.
Пример 3
Намерете разстоянието от дадена точка с координати M 1 (- 3, 2, - 7) до координатната равнина O x y z и равнината, дадена от уравнението 2 y - 5 = 0.
Решение
Координатната равнина O y z съответства на уравнение от вида x = 0. За равнината O y z е нормално. Следователно е необходимо да замените стойностите x = - 3 в лявата страна на израза и да вземете абсолютната стойност на разстоянието от точката с координати M 1 (- 3, 2, - 7) до равнината. Получаваме стойност, равна на - 3 = 3.
След трансформацията нормалното уравнение на равнината 2 y - 5 = 0 ще приеме формата y - 5 2 = 0. След това можете да намерите необходимото разстояние от точката с координати M 1 (- 3, 2, - 7) до равнината 2 y - 5 = 0. Като заместваме и пресмятаме, получаваме 2 - 5 2 = 5 2 - 2.
Отговор:Необходимото разстояние от M 1 (- 3, 2, - 7) до O y z има стойност 3, а до 2 y - 5 = 0 има стойност 5 2 - 2.
Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter
, Конкурс "Презентация към урока"
клас: 11
Презентация към урока
Назад напред
внимание! Визуализациите на слайдове са само за информационни цели и може да не представят всички характеристики на презентацията. Ако се интересувате от тази работа, моля, изтеглете пълната версия.
Цели:
- обобщаване и систематизиране на знанията и уменията на учениците;
- развитие на умения за анализ, сравнение, правене на заключения.
Оборудване:
- мултимедиен проектор;
- компютър;
- листове със задачни текстове
НАПРЕДЪК НА КЛАСА
I. Организационен момент
II. Етап на актуализиране на знанията(слайд 2)
Повтаряме как се определя разстоянието от точка до равнина
III. Лекция(слайдове 3-15)
В този урок ще разгледаме различни начини за намиране на разстоянието от точка до равнина.
Първи метод: изчисление стъпка по стъпка
Разстояние от точка M до равнина α:
– равно на разстоянието до равнината α от произволна точка P, лежаща на права a, която минава през точката M и е успоредна на равнината α;
– е равно на разстоянието до равнината α от произволна точка P, лежаща на равнината β, която минава през точката M и е успоредна на равнината α.
Ние ще решим следните проблеми:
№1. В куб A...D 1 намерете разстоянието от точка C 1 до равнината AB 1 C.

Остава да се изчисли стойността на дължината на сегмента O 1 N.

№2. В правилна шестоъгълна призма A...F 1, всички ръбове на която са равни на 1, намерете разстоянието от точка A до равнината DEA 1.


Следващ метод: обемен метод.
Ако обемът на пирамидата ABCM е равен на V, тогава разстоянието от точка M до равнината α, съдържаща ∆ABC, се изчислява по формулата ρ(M; α) = ρ(M; ABC) =
При решаване на задачи използваме равенството на обемите на една фигура, изразено по два различни начина.
Нека решим следния проблем:
№3. Ръбът AD на пирамидата DABC е перпендикулярен на основната равнина ABC. Намерете разстоянието от A до равнината, минаваща през средите на ръбовете AB, AC и AD, ако.


При решаване на проблеми координатен методразстоянието от точка M до равнината α може да се изчисли с помощта на формулата ρ(M; α) = ![]() , където M(x 0; y 0; z 0), а равнината е дадена от уравнението ax + by + cz + d = 0
, където M(x 0; y 0; z 0), а равнината е дадена от уравнението ax + by + cz + d = 0
Нека решим следния проблем:
№4. В единичен куб A...D 1 намерете разстоянието от точка A 1 до равнина BDC 1.
Нека въведем координатна система с начало в точка A, оста y ще минава по ръба AB, оста x по ръба AD, а оста z по ръба AA 1. Тогава координатите на точките B (0; 1; 0) D (1; 0; 0;) C 1 (1; 1; 1)
Нека създадем уравнение за равнина, минаваща през точки B, D, C 1.
Тогава – dx – dy + dz + d = 0 x + y – z – 1= 0. Следователно ρ = ![]()
Следният метод, който може да се използва за решаване на проблеми от този тип, е метод на проблеми с поддръжката.
Приложението на този метод се състои в използването на известни справочни задачи, които са формулирани като теореми.

Нека решим следния проблем:
№5. В единичен куб A...D 1 намерете разстоянието от точка D 1 до равнината AB 1 C.

Нека разгледаме приложението векторен метод.
№6. В единичен куб A...D 1 намерете разстоянието от точка A 1 до равнина BDC 1.


И така, разгледахме различни методи, които могат да се използват за решаване на този тип проблеми. Изборът на един или друг метод зависи от конкретната задача и вашите предпочитания.
IV. Групова работа
Опитайте да разрешите проблема по различни начини.
№1. Ръбът на куба A...D 1 е равен на . Намерете разстоянието от върха C до равнината BDC 1.
№2. В правилен тетраедър ABCD с ребро намерете разстоянието от точка A до равнината BDC
№3. В правилна триъгълна призма ABCA 1 B 1 C 1, чиито ръбове са равни на 1, намерете разстоянието от A до равнината BCA 1.
№4. В правилна четириъгълна пирамида SABCD, всички ръбове на която са равни на 1, намерете разстоянието от A до равнината SCD.
V. Обобщение на урока, домашна работа, размисъл
Нека разгледаме определена равнина π и произволна точка M 0 в пространството. Да изберем за самолета единичен нормален вектор n с началотов някаква точка M 1 ∈ π и нека p(M 0 ,π) е разстоянието от точката M 0 до равнината π. Тогава (фиг. 5.5)
р(М 0 ,π) = | pr n M 1 M 0 | = |nM 1 M 0 |, (5.8)
тъй като |n| = 1.
Ако равнината π е дадена в правоъгълна координатна система с нейното общо уравнение Ax + By + Cz + D = 0, тогава неговият нормален вектор е векторът с координати (A; B; C) и можем да изберем

Нека (x 0 ; y 0 ; z 0) и (x 1 ; y 1 ; z 1) са координатите на точките M 0 и M 1 . Тогава равенството Ax 1 + By 1 + Cz 1 + D = 0 е в сила, тъй като точката M 1 принадлежи на равнината и координатите на вектора M 1 M 0 могат да бъдат намерени: M 1 M 0 = (x 0 - x 1; y 0 - y 1; z 0 - z 1). Записване скаларно произведение nM 1 M 0 в координатна форма и преобразувайки (5.8), получаваме

тъй като Ax 1 + By 1 + Cz 1 = - D. И така, за да изчислите разстоянието от точка до равнина, трябва да замените координатите на точката в общото уравнение на равнината и след това да разделите абсолютната стойност на резултатът чрез нормализиращ фактор, равен на дължината на съответния нормален вектор.