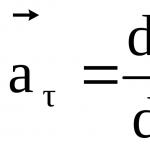Ускорението е тангенциално и нормално. Понятия за скорост, тангенциално и нормално ускорение

Тангенциално ускорениехарактеризира промяната на скоростта в абсолютна стойност (величина) и е насочена тангенциално към траекторията:

,

Където  производна на модула на скоростта,  единичен тангенс вектор, съвпадащ по посока със скоростта.

Нормално ускорениехарактеризира промяната на скоростта в посока и е насочена по радиуса на кривината към центъра на кривината на траекторията в дадена точка:

,

където R е радиусът на кривината на траекторията,  единичен нормален вектор.

Големината на вектора на ускорението може да се намери с помощта на формулата

.

1.3. Основната задача на кинематиката

Основната задача на кинематиката е да намери закона за движение на материална точка. За целта се използват следните отношения:

;
;
;
;

.

Специални случаи на праволинейно движение:

1) равномерно линейно движение: ;

2) равномерно линейно движение:
.

1.4. Въртеливото движение и неговите кинематични характеристики

При въртеливото движение всички точки на тялото се движат в кръгове, чиито центрове лежат на една и съща права линия, наречена ос на въртене. За характеризиране на въртеливото движение се въвеждат следните кинематични характеристики (фиг. 3).

Ъглово движение
 вектор, числено равен на ъгъла на завъртане на тялото
по време на
и насочена по оста на въртене, така че, гледайки по нея, се наблюдава въртенето на тялото по посока на часовниковата стрелка.

Ъглова скорост  характеризира скоростта и посоката на въртене на тялото, равна е на производната на ъгъла на въртене по отношение на времето и е насочена по оста на въртене като ъглово преместване.

П За въртеливото движение са валидни следните формули:

;
;
.

Ъглово ускорение характеризира скоростта на промяна на ъгловата скорост във времето, равна на първата производна на ъгловата скорост и насочена по оста на въртене:

;
;
.

Пристрастяване
изразява закона за въртене на тялото.

При равномерно въртене:  = 0,  = const,  = t.

При равномерно въртене:  = const,
,
.

За характеризиране на равномерно въртеливо движение се използват периодът на въртене и честотата на въртене.

Период на въртене T е времето за един оборот на тяло, въртящо се с постоянна ъглова скорост.

Честота на въртене – броят на оборотите, направени от тялото за единица време.

Ъгловата скорост може да се изрази, както следва:

.

Връзка между ъглови и линейни кинематични характеристики (фиг. 4):

2. Динамика на транслационни и ротационни движения

1. Законите на Нютон Първи закон на Нютон: всяко тяло е в състояние на покой или равномерно праволинейно движение, докато въздействието на други тела не го изведе от това състояние.

Телата, които не са подложени на външни въздействия, се наричат ​​свободни тела. Отправната система, свързана със свободно тяло, се нарича инерциална отправна система (IRS). Спрямо него всяко свободно тяло ще се движи равномерно и праволинейно или ще е в покой. От относителността на движението следва, че отправна система, която се движи равномерно и праволинейно по отношение на ISO, също е ISO. ISO играят важна роля във всички клонове на физиката. Това се дължи на принципа на относителността на Айнщайн, според който математическата форма на всеки физически закон трябва да има една и съща форма във всички инерционни отправни системи.

Основните понятия, използвани в динамиката на постъпателното движение, включват сила, маса на тялото и импулс на тялото (система от тела).

На силае векторна физическа величина, която е мярка за механичното въздействие на едно тяло върху друго. Механичното действие възниква както чрез директен контакт на взаимодействащи тела (триене, опорна реакция, тежест и др.), така и чрез силово полесъществуващи в пространството (гравитация, сили на Кулон и др.). Сила характеризира се с модул, посока и точка на приложение.

Едновременно действие на няколко сили върху тялото ,,...,може да се замени с действието на резултантната (резултантната) сила :

=++...+=.

масана тяло е скаларна величина, която е мярка инерциятела. Под инерциясе отнася до свойството на материалните тела да поддържат скоростта си непроменена при липса на външни влияния и да я променят постепенно (т.е. с ограничено ускорение) под въздействието на сила.

Импулстяло (материална точка) е векторно физическо количество, равно на произведението на масата на тялото и неговата скорост:
.

Импулсът на система от материални точки е равен на векторната сума на импулса на точките, които съставят системата:
.

Втори закон на Нютон: скоростта на промяна на импулса на тялото е равна на силата, действаща върху него:

.

Ако масата на тялото остане постоянна, тогава ускорението, придобито от тялото спрямо инерционната отправна система, е право пропорционално на силата, действаща върху него, и обратно пропорционално на масата на тялото:

.

Дадени са основните формули на кинематиката на материална точка, тяхното извеждане и представяне на теорията.

Вижте също: Пример за решаване на задача (координатен метод за определяне на движението на точка)

Основни формули за кинематиката на материална точка

Нека представим основните формули на кинематиката на материална точка. След което ще дадем тяхното заключение и представяне на теорията.

Радиус вектор на материалната точка M в правоъгълната координатна система Oxyz:
,
където са единични вектори (ортове) по посока на осите x, y, z.

Точкова скорост:
;
.
.
Единичен вектор в посоката, допирателна към траекторията на точка:
.

Точка на ускорение:
;
;
;
; ;

Тангенциално (тангенциално) ускорение:
;
;
.

Нормално ускорение:
;
;
.

Единичен вектор, насочен към центъра на кривината на траекторията на точката (по главната нормала):
.

Радиус вектор и точкова траектория

Нека разгледаме движението на материалната точка M. Нека изберем фиксирана правоъгълна координатна система Oxyz с център в някаква фиксирана точка O. Тогава позицията на точка M се определя еднозначно от нейните координати (x, y, z). Тези координати са компоненти на радиус вектора на материалната точка.

Радиус векторът на точка M е вектор, изтеглен от началото на фиксирана координатна система O до точка M.
,
където са единични вектори по посока на осите x, y, z.

Когато една точка се движи, координатите се променят с времето. Тоест те са функции на времето. След това системата от уравнения
(1)
може да се разглежда като уравнение на крива, дефинирана от параметрични уравнения. Такава крива е траекторията на точка.

Траекторията на материална точка е линията, по която се движи точката.

Ако точката се движи в равнина, тогава осите и координатните системи могат да бъдат избрани така, че да лежат в тази равнина. Тогава траекторията се определя от две уравнения

В някои случаи времето може да бъде елиминирано от тези уравнения. Тогава уравнението на траекторията ще има формата:
,
къде е някаква функция. Тази зависимост съдържа само променливите и . Не съдържа параметъра.

Скорост на материална точка

Според определението за скорост и определението за производна:

В механиката производните по отношение на времето се означават с точка над символа. Нека заместим тук израза за радиус вектора:
,
където ясно сме посочили зависимостта на координатите от времето. Получаваме:

,
Където
,
,

- проекции на скоростта върху координатните оси. Те се получават чрез диференциране на компонентите на радиус вектора по време
.

По този начин
.
Модул за скорост:
.

Допирателна към пътя

От математическа гледна точка системата от уравнения (1) може да се разглежда като уравнение на линия (крива), определена от параметрични уравнения. Времето в това отношение играе ролята на параметър. От курса на математическия анализ е известно, че векторът на посоката на допирателната към тази крива има компонентите:
.
Но това са компонентите на вектора на скоростта на точката. Това е скоростта на материалната точка е насочена тангенциално към траекторията.

Всичко това може да се демонстрира директно. Нека в момента точката е в позиция с радиус вектор (виж фигурата). И в момента - в позиция с радиус вектора. Нека начертаем права линия през точките. По дефиниция допирателната е права линия, към която правата клони като .
Нека въведем следната нотация:
;
;
.
Тогава векторът е насочен по правата линия.

Когато се стреми, правата линия се стреми към допирателната, а векторът се стреми към скоростта на точката в момента:
.
Тъй като векторът е насочен по правата линия, а правата линия към , векторът на скоростта е насочен по допирателната.
Тоест векторът на скоростта на материална точка е насочен по допирателната към траекторията.

Нека се запознаем допирателна посока вектор на единица дължина:
.
Нека покажем, че дължината на този вектор е равна на единица. Наистина, тъй като
, Че:
.

Тогава векторът на скоростта на точката може да бъде представен като:
.

Ускорение на материална точка

Подобно на предишния, получаваме компонентите на ускорението (проекции на ускорението върху координатните оси):
;
;
;
.
Модул за ускоряване:
.

Тангенциално (допирателно) и нормално ускорение

Сега разгледайте въпроса за посоката на вектора на ускорението по отношение на траекторията. За целта прилагаме формулата:
.
Ние го диференцираме по отношение на времето, като използваме правилото за диференциране на продукта:
.

Векторът е насочен тангенциално към траекторията. В каква посока е насочена неговата производна по време?

За да отговорим на този въпрос, използваме факта, че дължината на вектора е постоянна и равна на единица. Тогава квадратът на неговата дължина също е равен на едно:
.
Тук и по-долу два вектора в скоби означават скаларното произведение на векторите. Нека диференцираме последното уравнение по отношение на времето:
;
;
.
Тъй като скаларното произведение на векторите и е равно на нула, тези вектори са перпендикулярни един на друг. Тъй като векторът е насочен допирателна към траекторията, векторът е перпендикулярен на допирателната.

Първият компонент се нарича тангенциално или тангенциално ускорение:
.
Вторият компонент се нарича нормално ускорение:
.
Тогава общото ускорение е:
(2) .
Тази формула представлява разлагането на ускорението на две взаимно перпендикулярни компоненти - допирателна към траекторията и перпендикулярна към допирателната.

От тогава
(3) .

Тангенциално (тангенциално) ускорение

Нека умножим двете страни на уравнението (2) скалар до:
.
Защото тогава. Тогава
;
.
Тук поставяме:
.
От това можем да видим, че тангенциалното ускорение е равно на проекцията на пълното ускорение върху посоката на допирателната към траекторията или, което е същото, върху посоката на скоростта на точката.

Тангенциалното (тангенциалното) ускорение на материална точка е проекцията на нейното пълно ускорение върху посоката на допирателната към траекторията (или към посоката на скоростта).

Използваме символа, за да обозначим вектора на тангенциалното ускорение, насочен по допирателната към траекторията. Тогава е скаларна величина, равна на проекцията на пълното ускорение върху посоката на тангентата. Тя може да бъде както положителна, така и отрицателна.

Замествайки , имаме:
.

Нека го поставим във формулата:
.
Тогава:
.
Тоест тангенциалното ускорение е равно на производната по време на абсолютната скорост на точката. По този начин, тангенциалното ускорение води до промяна в абсолютната стойност на скоростта на точката. С увеличаване на скоростта тангенциалното ускорение е положително (или насочено по скоростта). Когато скоростта намалява, тангенциалното ускорение е отрицателно (или в посока, обратна на скоростта).

Сега нека разгледаме вектора.

Да разгледаме единичен вектор, допирателен към траекторията. Нека поставим началото му в началото на координатната система. Тогава краят на вектора ще бъде върху сфера с единичен радиус. Когато една материална точка се движи, краят на вектора ще се движи по тази сфера. Тоест ще се върти около началото си. Нека е моментната ъглова скорост на въртене на вектора в момента от време. Тогава неговата производна е скоростта на движение на края на вектора. Той е насочен перпендикулярно на вектора. Нека приложим формулата за въртеливо движение. Векторен модул:
.

Сега разгледайте позицията на точката за два близки момента във времето. Нека точката е в позиция в момента на времето и в позиция в момента на времето. Нека и са единични вектори, насочени тангенциално към траекторията в тези точки. През точките и начертаваме равнини, перпендикулярни на векторите и . Нека е права линия, образувана от пресичането на тези равнини. От точка спускаме перпендикуляр към права линия. Ако позициите на точките са достатъчно близки, тогава движението на точката може да се разглежда като въртене по окръжност с радиус около оста, която ще бъде моментната ос на въртене на материалната точка. Тъй като векторите и са перпендикулярни на равнините и, ъгълът между тези равнини е равен на ъгъла между векторите и. Тогава моментната скорост на въртене на точката около оста е равна на моментната скорост на въртене на вектора:
.
Ето разстоянието между точки и .

Така намерихме модула на времевата производна на вектора:
.
Както посочихме по-рано, векторът е перпендикулярен на вектора. От горните разсъждения става ясно, че тя е насочена към моментния център на кривината на траекторията. Тази посока се нарича главна нормала.

Нормално ускорение

Нормално ускорение

насочен по вектора. Както разбрахме, този вектор е насочен перпендикулярно на допирателната, към моментния център на кривината на траекторията.
Нека е единичен вектор, насочен от материалната точка към моментния център на кривината на траекторията (по главната нормала). Тогава
;
.
Тъй като и двата вектора имат една и съща посока - към центъра на кривината на траекторията, тогава
.

От формулата (2) ние имаме:
(4) .
От формулата (3) намираме модула за нормално ускорение:
.

Нека умножим двете страни на уравнението (2) скалар до:
(2) .
.
Защото тогава. Тогава
;
.
Това показва, че модулът на нормалното ускорение е равен на проекцията на пълното ускорение върху посоката на главната нормала.

Нормалното ускорение на материална точка е проекцията на нейното пълно ускорение върху посоката, перпендикулярна на допирателната към траекторията.

Да заместим. Тогава
.
Тоест нормалното ускорение предизвиква промяна в посоката на скоростта на дадена точка и е свързано с радиуса на кривината на траекторията.

От тук можете да намерите радиуса на кривина на траекторията:
.

И в заключение отбелязваме, че формулата (4) може да се пренапише, както следва:
.
Тук сме приложили формулата за кръстосаното произведение на три вектора:
,
които рамкираха
.

Така че имаме:
;
.
Нека приравним модулите на лявата и дясната част:
.
Но векторите също са взаимно перпендикулярни. Ето защо
.
Тогава
.
Това е добре позната формула от диференциалната геометрия за кривината на крива.

Кинематика на точка, кинематика на твърдо тяло, постъпателно движение, въртеливо движение, плоскопаралелно движение, теорема за проекциите на скоростта, моментен център на скоростите, определяне на скоростта и ускорението на точки от плоско тяло, сложно движение на точка

Кинематика на твърдото тяло

За да определите еднозначно позицията на твърдо тяло, трябва да посочите три координати (x A, y A, z A)една от точките А на тялото и три ъгъла на завъртане. Така положението на твърдото тяло се определя от шест координати. Тоест едно твърдо тяло има шест степени на свобода.

В общия случай зависимостта на координатите на точките върху твърдо тяло спрямо фиксирана координатна система се определя от доста тромави формули. Но скоростите и ускоренията на точките се определят доста просто. За да направите това, трябва да знаете зависимостта на координатите от времето на една произволно избрана точка А и вектора на ъгловата скорост. Диференцирайки по време, намираме скоростта и ускорението на точка А и ъгловото ускорение на тялото:
; ; .
Тогава скоростта и ускорението на точка от тяло с радиус вектор се определят по формулите:
(1) ;
(2) .
Тук и по-долу произведенията на вектори в квадратни скоби означават векторни произведения.

Забележи, че векторът на ъгловата скорост е еднакъв за всички точки на тялото. Не зависи от координатите на точките на тялото. Също векторът на ъгловото ускорение е еднакъв за всички точки на тялото.

Вижте изхода на формулата (1) И (2) на страница: Скорост и ускорение на точки на твърдо тяло > > >

Постъпателно движение на твърдо тяло

При постъпателно движение ъгловата скорост е нула. Скоростите на всички точки на тялото са еднакви. Всяка права линия, начертана в тялото, се движи, оставайки успоредна на първоначалната си посока. По този начин, за да се изследва движението на твърдо тяло по време на транслационно движение, е достатъчно да се изследва движението на всяка една точка от това тяло. Вижте раздел.

Равноускорено движение

Нека разгледаме случая на равномерно ускорено движение. Нека проекцията на ускорението на точка от тялото върху оста x е постоянна и равна на a x. Тогава проекцията на скоростта v x и x - координатата на тази точка зависи от времето t по закона:
v x = v x 0 + a x t;
,
където v x 0 и х 0 - скорост и координата на точката в началния момент от времето t = 0 .

Ротационно движение на твърдо тяло

Да разгледаме тяло, което се върти около фиксирана ос. Нека изберем фиксирана координатна система Oxyz с център в точка O. Нека насочим оста z по оста на въртене. Приемаме, че z-координатите на всички точки на тялото остават постоянни. Тогава движението става в равнината xy. Ъгловата скорост ω и ъгловото ускорение ε са насочени по оста z:
; .
Нека φ е ъгълът на завъртане на тялото, който зависи от времето t. Разграничавайки се по отношение на времето, намираме проекции на ъглова скорост и ъглово ускорениекъм оста z:
;
.

Да разгледаме движението на точка M, която се намира на разстояние r от оста на въртене. Траекторията на движение е окръжност (или дъга от окръжност) с радиус r.
Точкова скорост:
v = ωr.
Векторът на скоростта е насочен тангенциално към траекторията.
Тангенциално ускорение:
a τ = ε r .
Тангенциалното ускорение също е насочено тангенциално към траекторията.
Нормално ускорение:
.
Тя е насочена към оста на въртене О.
Пълно ускорение:
.
Тъй като векторите и са перпендикулярни един на друг, тогава модул за ускорение:
.

Равноускорено движение

При равномерно ускорено движение, при което ъгловото ускорение е постоянно и равно на ε, ъгловата скорост ω и ъгълът на завъртане φ се променят с времето t по закона:
ω = ω 0 + εt;
,
където ω 0 и φ 0 - ъглова скорост и ъгъл на завъртане в началния момент от време t = 0 .

Равнопаралелно движение на твърдо тяло

Плоскопаралелен или плосъке движение на твърдо тяло, при което всички негови точки се движат успоредно на някаква фиксирана равнина. Нека изберем правоъгълна координатна система Oxyz. Ще поставим осите x и y в равнината, в която се движат точките на тялото. Тогава всички z - координати на точките на тялото остават постоянни, z - компонентите на скоростите и ускоренията са равни на нула. Векторите на ъгловата скорост и ъгловото ускорение, напротив, са насочени по оста z. Техните x и y компоненти са нула.

Проекциите на скоростите на две точки от твърдо тяло върху ос, минаваща през тези точки, са равни една на друга.
v A cos α = v B cos β.

Моментален център на скоростта

Моментален център на скоросттае точката на равнинна фигура, чиято скорост в момента е нула.

За да определите позицията на моментния център на скоростите P на плоска фигура, трябва да знаете само посоките на скоростите и нейните две точки A и B. За да направите това, начертайте права линия през точка А, перпендикулярна на посоката на скоростта. През точка В прекарваме права линия, перпендикулярна на посоката на скоростта. Пресечната точка на тези линии е моментният център на скоростите P. Ъглова скорост на въртене на тялото:
.

Ако скоростите на две точки са успоредни една на друга, тогава ω = 0 . Скоростите на всички точки на тялото са равни една на друга (в даден момент от времето).

Ако скоростта на която и да е точка A на плоско тяло и нейната ъглова скорост ω са известни, тогава скоростта на произволна точка M се определя по формулата (1) , което може да бъде представено като сума от транслационно и ротационно движение:
,
където е скоростта на въртеливото движение на точка М спрямо точка А. Това е скоростта, която точка M би имала при въртене в окръжност с радиус |AM| с ъглова скорост ω, ако точка А беше неподвижна.
Модул на относителната скорост:
v MA = ω |AM| .
Векторът е насочен допирателно към окръжността с радиус |AM| с център в точка А.

Определянето на ускоренията на точките на плоско тяло се извършва по формулата (2) . Ускорението на всяка точка M е равно на векторната сума на ускорението на някаква точка A и ускорението на точка M по време на въртене около точка A, като се има предвид, че точка A е неподвижна:
.
може да се разложи на тангенциални и нормални ускорения:
.
Тангенциалното ускорение е насочено тангенциално към траекторията. Нормалното ускорение е насочено от точка М към точка А. Тук ω и ε са ъгловата скорост и ъгловото ускорение на тялото.

Сложно точково движение

Нека О 1 x 1 y 1 z 1- фиксирана правоъгълна координатна система. Скоростта и ускорението на точка М в тази координатна система ще се наричат ​​абсолютна скорост и абсолютно ускорение.

Нека Oxyz е движеща се правоъгълна координатна система, да речем, твърдо свързана с определено твърдо тяло, движещо се спрямо системата O 1 x 1 y 1 z 1. Скоростта и ускорението на точка M в координатната система Oxyz ще се наричат ​​относителна скорост и относително ускорение. Нека е ъгловата скорост на въртене на системата Oxyz спрямо O 1 x 1 y 1 z 1.

Нека разгледаме точка, която в даден момент от времето съвпада с точка M и е неподвижна спрямо системата Oxyz (точка, твърдо свързана с твърдо тяло). Скорост и ускорение на такава точка в координатната система O 1 x 1 y 1 z 1ще го наречем преносима скорост и преносимо ускорение.

Теорема за добавяне на скорост

Абсолютната скорост на точка е равна на векторната сума на относителната и преносимата скорости:
.

Теорема за добавяне на ускорение (теорема на Кориолис)

Абсолютното ускорение на точка е равно на векторната сума на относителното, транспортното и Кориолисовото ускорение:
,
Където
- Кориолисово ускорение.

Препратки:
С. М. Тарг, Кратък курс по теоретична механика, “Висше училище”, 2010 г.

Линейно движение, линейна скорост, линейно ускорение.

Движещ се(в кинематиката) - промяна в местоположението на физическо тяло в пространството спрямо избраната референтна система. Векторът, характеризиращ тази промяна, се нарича още изместване. Има свойството на адитивност. Дължината на сегмента е модулът на преместване, измерен в метри (SI).

Можете да дефинирате движението като промяна в радиус вектора на точка: .

Модулът на преместване съвпада с изминатото разстояние тогава и само ако посоката на преместване не се променя по време на движение. В този случай траекторията ще бъде сегмент от права линия. Във всеки друг случай, например при криволинейно движение, от неравенството на триъгълника следва, че пътят е строго по-дълъг.

векторд r = r -r 0, изтеглен от началната позиция на движещата се точка до нейната позиция в даден момент (увеличаване на радиус вектора на точката през разглеждания период от време), се нарича движещ се.

При праволинейно движение векторът на преместване съвпада със съответния участък от траекторията и модула на преместване |D r| равно на изминатото разстояние D с.
Линейна скорост на тялото в механиката

Скорост

За характеризиране на движението на материална точка се въвежда векторна величина - скорост, която се определя като бързинадвижение и неговото посокав даден момент от времето.

Нека материална точка се движи по някаква криволинейна траектория, така че в момента на времето Tтой съответства на радиус вектора r 0 (фиг. 3). За кратък период от време Д Tточката ще върви по пътя D си ще получи елементарно (безкрайно малко) изместване Dr.

Вектор на средната скорост е отношението на увеличението Dr на радиус вектора на точка към интервала от време D T:

Посоката на вектора на средната скорост съвпада с посоката на Dr. С неограничено намаляване на D Tсредната скорост клони към гранична стойност нар моментна скорост v:

Следователно моментната скорост v е векторна величина, равна на първата производна на радиус-вектора на движещата се точка по отношение на времето. Тъй като секансът в границата съвпада с тангентата, векторът на скоростта v е насочен допирателно към траекторията в посоката на движение (фиг. 3). Тъй като D намалява Tпът D свсе повече ще се доближава до |Dr|, така че абсолютната стойност на моментната скорост

Така абсолютната стойност на моментната скорост е равна на първата производна на пътя по отношение на времето:

При неравномерно движение -модулът на моментната скорост се променя с времето. В този случай използваме скаларната величина b vñ - Средната скоростнеравномерно движение:

От фиг. 3 следва, че á vñ> |ávñ|, тъй като D с> |Dr|, и то само при праволинейно движение

Ако израз d s = vд T(вижте формула (2.2)) интегрирайте във времето, вариращи от Tпреди T+D T, тогава намираме дължината на пътя, изминат от точката във времето D T:

Кога равномерно движениечислената стойност на моментната скорост е постоянна; тогава изразът (2.3) ще приеме формата

Дължината на пътя, изминат от точка за периода от време от T 1 към T 2, зададена от интеграла

Ускорението и неговите компоненти

В случай на неравномерно движение е важно да знаете колко бързо се променя скоростта във времето. Физическа величина, характеризираща скоростта на промяна на скоростта по големина и посока е ускорение.

Нека помислим плоско движение,тези. движение, при което всички части от траекторията на точка лежат в една и съща равнина. Нека векторът v определя скоростта на точката Ав даден момент T.През времето Д Tдвижещата се точка се е преместила на позиция INи придобива скорост, различна от v както по големина, така и по посока и равна на v 1 = v + Dv. Нека преместим вектора v 1 до точката Аи намерете Dv (фиг. 4).

Средно ускорениенеравномерно движение в диапазона от Tпреди T+D Tе векторна величина, равна на отношението на промяната на скоростта Dv към интервала от време D T

Незабавно ускорениеи (ускорение) на материална точка в момента на времето Tще има ограничение на средното ускорение:

По този начин ускорението a е векторно количество, равно на първата производна на скоростта по отношение на времето.

Нека разложим вектора Dv на две компоненти. За да направите това от точката А(фиг. 4) по посока на скоростта v нанасяме вектора, равен по абсолютна стойност на v 1 . Очевидно векторът , равно на , определя промяната в скоростта във времето D t по модул: . Вторият компонент на вектора Dv характеризира промяната на скоростта във времето D t в посока.

Тангенциално и нормално ускорение.

Тангенциално ускорение- компонент на ускорението, насочен тангенциално към траекторията на движение. Съвпада с посоката на вектора на скоростта при ускорено движение и в обратната посока при бавно движение. Характеризира промяната в скоростния модул. Обикновено се обозначава или ( и т.н. в съответствие с това коя буква е избрана за обозначаване на ускорението като цяло в този текст).

Понякога тангенциалното ускорение се разбира като проекцията на вектора на тангенциалното ускорение - както е дефинирано по-горе - върху единичния вектор на допирателната към траекторията, който съвпада с проекцията на вектора на (общото) ускорение върху единичния вектор на допирателната, т.е. съответния коефициент на разширение в придружаващата основа. В този случай не се използва векторна нотация, а „скаларна“ - както обикновено за проекцията или координатите на вектор - .

Големината на тангенциалното ускорение - в смисъла на проекцията на вектора на ускорението върху единичен тангенциален вектор на траекторията - може да се изрази, както следва:

където е земната скорост по траекторията, съвпадаща с абсолютната стойност на моментната скорост в даден момент.

Ако използваме нотацията за единичния тангенциален вектор, тогава можем да запишем тангенциалното ускорение във векторна форма:

Заключение

Изразът за тангенциалното ускорение може да бъде намерен чрез диференциране по отношение на времето на вектора на скоростта, представен чрез единичния тангенциален вектор:

където първият член е тангенциалното ускорение, а вторият е нормалното ускорение.

Тук използваме обозначението за единичния вектор на нормалата към траекторията и - за текущата дължина на траекторията (); последният преход също използва очевидното

и от геометрични съображения,

Центростремително ускорение (нормално)- част от общото ускорение на точка, дължащо се на кривината на траекторията и скоростта на движение на материалната точка по нея. Това ускорение е насочено към центъра на кривината на траекторията, което е причината за термина. Формално и по същество терминът центростремително ускорение като цяло съвпада с термина нормално ускорение, различавайки се по-скоро само стилистично (понякога исторически).

Особено често говорим за центростремително ускорение, когато говорим за равномерно движение в кръг или когато движението е повече или по-малко близко до този конкретен случай.

Елементарна формула

където е нормалното (центростремително) ускорение, е (моментната) линейна скорост на движение по траекторията, е (моментната) ъглова скорост на това движение спрямо центъра на кривината на траекторията, е радиусът на кривината на траекторията в дадена точка. (Връзката между първата формула и втората е очевидна, дадено).

Горните изрази включват абсолютни стойности. Те могат лесно да бъдат записани във векторна форма чрез умножаване по - единичен вектор от центъра на кривината на траекторията до дадена точка:

Тези формули са еднакво приложими както за случай на движение с постоянна (по абсолютна стойност) скорост, така и за произволен случай. Във втория обаче трябва да се има предвид, че центростремителното ускорение не е пълният вектор на ускорението, а само неговият компонент, перпендикулярен на траекторията (или, което е същото, перпендикулярен на вектора на моментната скорост); тогава векторът на пълното ускорение включва и тангенциална компонента (тангенциално ускорение), като посоката съвпада с допирателната към траекторията (или, което е същото, с моментната скорост).

Заключение

Фактът, че разлагането на вектора на ускорението на компоненти - един по допирателната към векторната траектория (тангенциално ускорение) и другият, ортогонален на него (нормално ускорение) - може да бъде удобно и полезно, е съвсем очевиден сам по себе си. Това се утежнява от факта, че при движение с постоянна скорост тангенциалната компонента ще бъде равна на нула, тоест в този важен частен случай остава само нормалната компонента. Освен това, както може да се види по-долу, всеки от тези компоненти има ясно определени свойства и структура, а нормалното ускорение съдържа доста важно и нетривиално геометрично съдържание в структурата на своята формула. Да не говорим за важния частен случай на движение в кръг (който освен това може да се обобщи до общия случай практически без промени).

Тангенциално (тангенциално) ускорение – това е компонентът на вектора на ускорението, насочен по допирателната към траекторията в дадена точка от траекторията на движение. Тангенциалното ускорение характеризира промяната на скоростта по модул по време на криволинейно движение.

Фигура 1 – Тангенциално ускорение

Посоката на вектора на тангенциалното ускорение съвпада с посоката на линейната скорост или е противоположна на нея, от фиг. 1. Тоест векторът на тангенциалното ускорение лежи на една и съща ос с допирателната окръжност, която е траекторията на тялото.

Нормално ускорение е компонентът на вектора на ускорението, насочен по нормалата към траекторията на движение в дадена точка от траекторията на тялото. Тоест векторът на нормалното ускорение е перпендикулярен на линейната скорост на движение, показана на фиг. 1. Нормалното ускорение характеризира изменението на скоростта по посока и се означава с n. Векторът на нормалното ускорение е насочен по радиуса на кривината на траекторията.

Пълно ускорение при криволинейно движение се състои от тангенциални и нормални ускорения съгласно правилото за добавяне на вектори и се определя по формулата:

(9)

(10)

Посоката на пълното ускорение също се определя от правилото за добавяне на вектори:

(11)

1.1.5 Постъпателно и въртеливо движение на абсолютно твърдо тяло

Движението на тялото се счита за прогресивно, ако всеки сегмент от права линия, твърдо свързан с тялото, се движи постоянно успоредно на себе си. При постъпателно движение всички точки на тялото извършват еднакви движения, изминават едни и същи пътища, имат еднакви скорости и ускорения и описват еднакви траектории.

Въртене на твърдо тяло около неподвижна ос- движение, при което всички точки на тялото описват окръжности, чиито центрове са на една и съща права линия, перпендикулярна на равнините на тези окръжности. Самата тази права линия е оста на въртене.

Когато едно тяло се върти, радиусът на окръжността, описана от точка на това тяло, ще се завърти на определен ъгъл за интервал от време. Поради неизменността на взаимното разположение на точките на тялото, радиусите на окръжностите, описани от всяка друга точка на тялото, се завъртат на същия ъгъл за едно и също време. Този ъгъл е стойност, която характеризира въртеливото движение на цялото тяло като цяло. От това можем да заключим, че за да опишете въртеливото движение на абсолютно твърдо тяло около фиксирана ос, трябва да знаете само една променлива - ъгълът, под който тялото ще се върти за определено време.

Връзката между линейната и ъгловата скорост за всяка точка на твърдо тяло се дава по формулата:

(12)