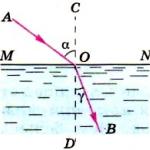
Векторен поток на електрическа индукция. Теорема на Гаус. Извеждане на теоремата на Остроградски–Гаус

Векторен поток на напрегнатост на електрическото поле.Нека малка платформа дС(фиг. 1.2) пресичат силовите линии електрическо поле, чиято посока е с нормалата н ъгъл към този сайт а. Ако приемем, че векторът на опън д не се променя в рамките на сайта дС, да дефинираме векторен поток на напрежениепрез платформата дСкак

дЕд =д дС cos а.(1.3)

Тъй като плътността на електропроводите е равна на числената стойност на напрежението д, след това броя на електропроводите, пресичащи районадС, ще бъде числено равна на стойността на потокадЕдпрез повърхносттадС. Нека представим дясната страна на израз (1.3) като скаларно произведение на вектори дИдС= ндС, Където н– единичен вектор нормален към повърхносттадС. За елементарна площ d Сизраз (1.3) приема формата

дЕд = дд С

В целия сайт Спотокът на вектора на опън се изчислява като интеграл по повърхността

Вектор на потока електрическа индукция. Потокът на вектора на електрическата индукция се определя подобно на потока на вектора на напрегнатостта на електрическото поле

дЕд = дд С

Има известна неяснота в дефинициите на потоците поради факта, че за всяка повърхност две нормали в обратна посока. За затворена повърхност външната нормала се счита за положителна.

Теорема на Гаус.Нека помислим точка положителнаелектрически заряд р, разположена вътре в произволна затворена повърхност С(фиг. 1.3). Индукционен векторен поток през повърхностния елемент d Сравно на
(1.4)

Компонент d S D = д С cos аповърхностен елемент d Спо посока на индукционния вектордразглежда като елемент от сферична повърхност с радиус r, в центъра на който се намира зарядътр.

Като се има предвид, че d S D/ r 2 е равно елементарно телесноъгъл dw, под който от точката, където се намира заррвидим повърхностен елемент d С, трансформираме израз (1.4) във форматад Ед = р д w / 4 стр, откъдето след интегриране по цялото пространство около заряда, т.е. в рамките на телесния ъгъл от 0 до 4стр, получаваме

Ед = р.

Потокът на вектора на електрическата индукция през затворена повърхност с произволна форма е равен на заряда, съдържащ се вътре в тази повърхност.

Ако произволна затворена повърхност Сне покрива точкова такса р(Фиг. 1.4), след което, след като изградихме конична повърхност с върха в точката, където се намира зарядът, разделяме повърхността Сна две части: С 1 и С 2. Вектор на потока д през повърхността Снамираме като алгебрична сума на потоците през повърхностите С 1 и С 2:

.

И двете повърхности от точката, където се намира зарядът рвидим от един плътен ъгъл w. Следователно потоците са равни

Тъй като при изчисляване на потока през затворена повърхност, ние използваме външна нормана повърхността е лесно да се види, че потокът F 1D < 0, тогда как поток Ф2D> 0. Общ поток Ф д= 0. Това означава, че потокът на вектора на електрическата индукция през затворена повърхност с произволна форма не зависи от зарядите, разположени извън тази повърхност.

Ако електричното поле е създадено от система от точкови заряди р 1 , р 2 ,¼ , qn, която е покрита със затворена повърхност С, тогава, в съответствие с принципа на суперпозиция, потокът на индукционния вектор през тази повърхност се определя като сумата от потоците, създадени от всеки от зарядите. Потокът на вектора на електрическата индукция през затворена повърхност с произволна форма е равен на алгебричната сума на зарядите, обхванати от тази повърхност:

Трябва да се отбележи, че таксите цине трябва да са точкови, необходимо условие- заредената зона трябва да бъде изцяло покрита от повърхността. Ако в пространство, ограничено от затворена повърхност С, електрическият заряд се разпределя непрекъснато, тогава трябва да се приеме, че всеки елементарен обем d Vима такса. В този случай, от дясната страна на израз (1.5), алгебричното сумиране на зарядите се заменя с интегриране върху обема, затворен вътре в затворена повърхност С:

(1.6)

Изразът (1.6) е най-общата формулировка Теорема на Гаус: потокът на вектора на електрическата индукция през затворена повърхност с произволна форма е равен на общия заряд в обема, покрит от тази повърхност, и не зависи от зарядите, разположени извън разглежданата повърхност. Теоремата на Гаус може да бъде написана и за потока на вектора на напрегнатост на електрическото поле:

.

Важно свойство на електрическото поле следва от теоремата на Гаус: силовите линии започват или завършват само с електрически заряди или отиват до безкрайност. Нека подчертаем още веднъж, че въпреки факта, че напрегнатостта на електрическото поле д и електрическа индукция д зависят от местоположението в пространството на всички заряди, потоците на тези вектори през произволна затворена повърхност Ссе определят само тези заряди, които се намират вътре в повърхността С.

Диференциална форма на теоремата на Гаус.Забележи, че интегрална формаТеоремата на Гаус характеризира връзката между източниците на електрическо поле (заряди) и характеристиките на електрическото поле (напрежение или индукция) в обема Vпроизволна, но достатъчна за формирането на интегрални отношения, величина. Чрез разделяне на обема Vза малки обеми V i, получаваме израза

валидни както като цяло, така и за всеки срок. Нека трансформираме получения израз, както следва:

(1.7)

и разгледайте границата, към която изразът от дясната страна на равенството, ограден във къдрави скоби, клони за неограничено разделяне на обема V. В математиката тази граница се нарича разминаваневектор (в в такъв случайвектор на електрическа индукция д):

Векторна дивергенция дв декартови координати:

Така изразът (1.7) се трансформира във вида:

.

Като се има предвид, че при неограничено деление сумата от лявата страна на последния израз преминава в обемен интеграл, получаваме

Получената връзка трябва да бъде изпълнена за всеки произволно избран обем V. Това е възможно само ако стойностите на интеграндите във всяка точка на пространството са еднакви. Следователно дивергенцията на вектора де свързано с плътността на заряда в същата точка чрез равенството

или за вектора на напрегнатост на електростатичното поле

Тези равенства изразяват теоремата на Гаус в диференциална форма.

Обърнете внимание, че в процеса на преход към диференциалната форма на теоремата на Гаус се получава връзка, която има общ характер:

.

Изразът се нарича формула на Гаус-Остроградски и свързва обемния интеграл на дивергенцията на вектор с потока на този вектор през затворена повърхност, ограничаваща обема.

Въпроси

1) Какво е физически смисълТеорема на Гаус за електростатичното поле във вакуум

2) В центъра на куба има точков зарядр. Какъв е потокът на вектор? д:

а) през цялата повърхност на куба; б) през една от страните на куба.

Ще се променят ли отговорите, ако:

а) зарядът не е в центъра на куба, а вътре в него ; б) зарядът е извън куба.

3) Какво представляват линейната, повърхностната, обемната плътност на заряда.

4) Посочете връзката между плътността на обема и повърхностния заряд.

5) Може ли полето извън противоположно и равномерно заредени паралелни безкрайни равнини да бъде различно от нула?

6) Електрически дипол е поставен вътре в затворена повърхност. Какъв е потокът през тази повърхност

Когато има много заряди, възникват някои трудности при изчисляването на полета.

Теоремата на Гаус помага за преодоляването им. Същността Теорема на Гауссе свежда до следното: ако произволен брой заряди са мислено заобиколени от затворена повърхност S, тогава потокът от напрегнатост на електрическото поле през елементарна област dS може да бъде записан като dФ = Есоsα۰dS, където α е ъгълът между нормалата към равнина и вектор на якост . (фиг. 12.7)

Общият поток през цялата повърхност ще бъде равен на сумата от потоците от всички заряди, произволно разпределени вътре в нея, и пропорционален на големината на този заряд

(12.9)

Нека определим потока на вектора на интензитета през сферична повърхност с радиус r, в центъра на която е разположен точков заряд +q (фиг. 12.8). Линиите на опън са перпендикулярни на повърхността на сферата, α = 0, следователно cosα = 1. Тогава

Ако полето е образувано от система от заряди, тогава

Теорема на Гаус: потокът на вектора на напрегнатост на електростатичното поле във вакуум през всяка затворена повърхност е равен на алгебричната сума на зарядите, съдържащи се вътре в тази повърхност, разделена на електрическата константа.

(12.10)

Ако вътре в сферата няма заряди, тогава Ф = 0.

Теоремата на Гаус прави сравнително лесно изчисляването на електрически полета за симетрично разпределени заряди.

Нека въведем концепцията за плътността на разпределените заряди.

Линейната плътност се означава с τ и характеризира заряда q на единица дължина ℓ. IN общ изгледможе да се изчисли с помощта на формулата

(12.11)

При равномерно разпределение на зарядите линейната плътност е равна на

Повърхностната плътност се означава с σ и характеризира заряда q на единица площ S. Най-общо се определя по формулата

(12.12)

При равномерно разпределение на зарядите по повърхността, повърхностната плътност е равна на

Обемната плътност се означава с ρ и характеризира заряда q на единица обем V. Най-общо се определя по формулата

(12.13)

При равномерно разпределение на зарядите тя е равна на
.

Тъй като зарядът q е равномерно разпределен върху сферата, тогава

σ = const. Нека приложим теоремата на Гаус. Нека начертаем сфера с радиус през точка A. Потокът на вектора на опън на фиг. 12.9 през сферична повърхност с радиус е равен на cosα = 1, тъй като α = 0. Според теоремата на Гаус,
.

или

(12.14)

От израза (12.14) следва, че напрегнатостта на полето извън заредената сфера е същата като напрегнатостта на полето на точков заряд, поставен в центъра на сферата. На повърхността на сферата, т.е. r 1 = r 0, напрежение
.

Вътре в сферата r 1< r 0 (рис.12.9) напряжённость Е = 0, так как сфера радиусом r 2 внутри никаких зарядов не содержит и, по теореме Гаусса, поток вектора сквозь такую сферу равен нулю.

Цилиндър с радиус r 0 е равномерно зареден с повърхностна плътност σ (фиг. 12.10). Нека определим напрегнатостта на полето в произволно избрана точка A. Нека начертаем въображаема цилиндрична повърхност с радиус R и дължина ℓ през точка A. Поради симетрията потокът ще излезе само през страничните повърхности на цилиндъра, тъй като зарядите върху цилиндъра с радиус r 0 са разпределени равномерно по повърхността му, т.е. линиите на напрежение ще бъдат радиални прави линии, перпендикулярни на страничните повърхности на двата цилиндъра. Тъй като потокът през основата на цилиндрите е нула (cos α = 0), а страничната повърхност на цилиндъра е перпендикулярна на силовите линии (cos α = 1), тогава

или

(12.15)

Нека изразим стойността на E чрез σ - повърхностна плътност. A-приори,

следователно,

Нека заместим стойността на q във формула (12.15)

(12.16)

По дефиницията на линейната плътност,
, където
; заместваме този израз във формула (12.16):

(12.17)

тези. Силата на полето, създадено от безкрайно дълъг зареден цилиндър, е пропорционална на линейната плътност на заряда и обратно пропорционална на разстоянието.

Сила на полето, създадена от безкрайна равномерно заредена равнина

Нека определим напрегнатостта на полето, създадено от безкрайна равномерно заредена равнина в точка А. Нека повърхностната плътност на заряда на равнината е равна на σ. Като затворена повърхност е удобно да изберете цилиндър, чиято ос е перпендикулярна на равнината и чиято дясна основа съдържа точка А. Равнината разделя цилиндъра наполовина. Очевидно силовите линии са перпендикулярни на равнината и успоредни на страничната повърхност на цилиндъра, така че целият поток преминава само през основата на цилиндъра. И на двете бази силата на полето е еднаква, т.к точки A и B са симетрични спрямо равнината. Тогава потокът през основата на цилиндъра е равен на

Според теоремата на Гаус,

защото
, Че
, където

(12.18)

По този начин силата на полето на безкрайно заредена равнина е пропорционална на повърхностната плътност на заряда и не зависи от разстоянието до равнината. Следователно полето на равнината е равномерно.

Сила на полето, създадена от две противоположно еднакво заредени успоредни равнини

Полученото поле, създадено от две равнини, се определя от принципа на суперпозицията на полето:
(фиг. 12.12). Полето, създадено от всяка равнина, е еднакво, силите на тези полета са еднакви по големина, но противоположни по посока:
. Съгласно принципа на суперпозицията общата напрегнатост на полето извън равнината е нула:

Между равнините напрегнатостта на полето има еднакви посоки, така че получената сила е равна на

По този начин полето между две различно заредени равнини е еднакво и неговият интензитет е два пъти по-силен от интензитета на полето, създадено от една равнина. Отляво и отдясно на самолетите няма поле. Полето на крайните равнини има същата форма, изкривяването се появява само в близост до техните граници. Използвайки получената формула, можете да изчислите полето между плочите на плосък кондензатор.

Основната приложна задача на електростатиката е изчисляването на електрически полета, създадени в различни устройства и устройства. Като цяло този проблем се решава с помощта на закона на Кулон и принципа на суперпозицията. Тази задача обаче става много трудна при разглеждане голямо числоточкови или пространствено разпределени заряди. Още по-големи трудности възникват, когато в пространството има диелектрици или проводници, когато под въздействието на външно поле E 0 възниква преразпределение на микроскопични заряди, създавайки собствено допълнително поле E. Следователно, за практическото решаване на тези проблеми, спомагателните методи и техники са използвани, които използват сложен математически апарат. Ще разгледаме най-простия метод, основан на прилагането на теоремата на Остроградски-Гаус. За да формулираме тази теорема, въвеждаме няколко нови концепции:

А) плътност на заряда

Ако зареденото тяло е голямо, тогава трябва да знаете разпределението на зарядите вътре в тялото.

Обемна плътност на заряда– измерено чрез заряда на единица обем:

Плътност на повърхностния заряд– измерено чрез заряд на единица повърхност на тяло (когато зарядът е разпределен по повърхността):

Линейна плътност на заряда(разпределение на заряда по протежение на проводника):

б) вектор на електростатична индукция

Вектор на електростатична индукция (вектор на електрическо изместване) е векторна величина, характеризираща електрическото поле.

вектор равно на произведението на вектора върху абсолютната диелектрична проницаемост на средата в дадена точка:

Нека проверим измерението дв единици SI:

, защото
,

тогава размерите D и E не съвпадат и техните числени стойности също са различни.

От дефиницията следва, че за векторното поле важи същият принцип на суперпозиция, както за полето :

Поле графично представени чрез индукционни линии, точно като полето . Индукционните линии са начертани така, че допирателната във всяка точка да съвпада с посоката , а броят на линиите е равен на числената стойност на D на дадено място.

Да разберем смисъла на въведението Нека разгледаме един пример.

V) векторен поток на електростатична индукция

Разгледайте повърхността S в електрическо поле и изберете посоката на нормалата

1. Ако полето е равномерно, тогава броят на линиите на полето през повърхността S:

2. Ако полето е нееднородно, тогава повърхността се разделя на безкрайно малки елементи dS, които се считат за плоски и полето около тях е еднородно. Следователно потокът през повърхностния елемент е: dN = D n dS,

и общият поток през всяка повърхност е:

(6)

Индукционният поток N е скаларна величина; в зависимост от  може да бъде > 0 или< 0, или = 0.

Обща формулировка: Потокът на вектора на напрегнатост на електрическото поле през всяка произволно избрана затворена повърхност е пропорционален на електрическия заряд, съдържащ се вътре в тази повърхност.

В системата SGSE:

В системата SI:

е потокът на вектора на напрегнатост на електрическото поле през затворена повърхност.

- общият заряд, съдържащ се в обема, който ограничава повърхността.

- електрическа константа.

Този израз представлява теоремата на Гаус в интегрална форма.

В диференциална форма теоремата на Гаус съответства на едно от уравненията на Максуел и се изразява по следния начин

в системата SI:

,

в системата SGSE:

Тук е обемната плътност на заряда (в случай на наличие на среда, общата плътност на свободните и свързаните заряди) и е операторът nabla.

За теоремата на Гаус е валиден принципът на суперпозицията, т.е. потокът на вектора на интензитета през повърхността не зависи от разпределението на заряда вътре в повърхността.

Физическата основа на теоремата на Гаус е законът на Кулон или, с други думи, теоремата на Гаус е интегрална формулировка на закона на Кулон.

Теорема на Гаус за електрическа индукция (електрическо изместване).

За поле в материята електростатична теоремаГаусът може да бъде написан по различен начин - чрез потока на вектора на електрическото изместване (електрическа индукция). В този случай формулировката на теоремата е следната: потокът на вектора на електрическото изместване през затворена повърхност е пропорционален на свободния електрически заряд, съдържащ се вътре в тази повърхност:

Ако разгледаме теоремата за силата на полето в веществото, тогава като заряд Q е необходимо да вземем сумата от свободния заряд, разположен вътре в повърхността, и поляризационния (индуциран, свързан) заряд на диелектрика:

,

Където ,
е поляризационният вектор на диелектрика.

Теорема на Гаус за магнитна индукция

Потокът на вектора на магнитната индукция през всяка затворена повърхност е нула:

.

Това е еквивалентно на факта, че в природата няма „магнитни заряди“ (монополи), които биха създали магнитно поле, напр. електрически зарядисъздават електрическо поле. С други думи, теоремата на Гаус за магнитната индукция показва, че магнитното поле е вихрово.

Приложение на теоремата на Гаус

За изчисляване на електромагнитните полета се използват следните величини:

Обемна плътност на заряда (виж по-горе).

Плътност на повърхностния заряд

където dS е безкрайно малка повърхност.

Линейна плътност на заряда

където dl е дължината на безкрайно малък сегмент.

Нека разгледаме полето, създадено от безкрайна еднакво заредена равнина. Нека повърхностната плътност на заряда на равнината е еднаква и равна на σ. Нека си представим цилиндър с образуващи, перпендикулярни на равнината, и основа ΔS, разположена симетрично спрямо равнината. Поради симетрията. Потокът на вектора на опън е равен на . Прилагайки теоремата на Гаус, получаваме:

,

от кое

в системата SSSE

Важно е да се отбележи, че въпреки своята универсалност и обобщеност, теоремата на Гаус в интегрална форма има относително ограничено приложение поради неудобството при изчисляване на интеграла. Въпреки това, в случай на симетричен проблем, неговото решение става много по-просто от използването на принципа на суперпозицията.

Теорема на Гаус за електрическа индукция (електрическо изместване)[

За поле в диелектрична среда електростатичната теорема на Гаус може да се напише по друг начин (по алтернативен начин) - чрез потока на вектора на електрическото отместване (електрическа индукция). В този случай формулировката на теоремата е следната: потокът на вектора на електрическото изместване през затворена повърхност е пропорционален на свободния електрически заряд, съдържащ се вътре в тази повърхност:

В диференциална форма:

Теорема на Гаус за магнитна индукция

Потокът на вектора на магнитната индукция през всяка затворена повърхност е нула:

или в диференциална форма

Това е еквивалентно на факта, че в природата няма „магнитни заряди“ (монополи), които биха създали магнитно поле, както електрическите заряди създават електрическо поле. С други думи, теоремата на Гаус за магнитната индукция показва, че магнитното поле е (напълно) вихър.

Теорема на Гаус за Нютоновата гравитация

За силата на полето на нютоновата гравитация (гравитационното ускорение) теоремата на Гаус практически съвпада с тази в електростатиката, с изключение само на константи (които обаче все още зависят от произволния избор на системата от единици) и, най-важното, знака:

Където ж- напрегнатост на гравитационното поле, М- гравитационен заряд (т.е. маса) вътре в повърхността С, ρ - плътност на масата, Ж- Нютонова константа.

Проводници в електрическо поле. Поле вътре в проводник и на повърхността му.

Проводниците са тела, през които електрическите заряди преминават от заредено тяло към незаредено.Способността на проводниците да пропускат електрически заряди през себе си се обяснява с наличието на свободни носители на заряд в тях. Проводници - метални тела в твърдо и течно състояние, течни разтвори на електролити. Свободните заряди на проводник, въведен в електрическо поле, започват да се движат под негово влияние. Преразпределението на зарядите предизвиква промяна в електрическото поле. Когато напрегнатостта на електрическото поле в проводник стане нула, електроните спират да се движат. Феноменът на разделяне на различни заряди в проводник, поставен в електрическо поле, се нарича електростатична индукция. Вътре в проводника няма електрическо поле. Това се използва за електростатична защита - защита с помощта на метални проводници от електрическо поле. Повърхността на проводящо тяло с произволна форма в електрическо поле е еквипотенциална повърхност.

Кондензатори

За да получат устройства, които при нисък потенциал спрямо средата биха натрупали (кондензирали) забележими заряди върху себе си, те използват факта, че електрическият капацитет на проводника се увеличава, когато други тела се приближават към него. Наистина, под въздействието на полето, създадено от заредени проводници, индуцирани (върху проводника) или свързани (върху диелектрика) заряди се появяват върху тялото, доведено до него (фиг. 15.5). Зарядите, противоположни по знак на заряда на проводника q, са разположени по-близо до проводника, отколкото тези със същото име с q и следователно имат голямо влияние върху неговия потенциал.

Следователно, когато някое тяло се доближи до зареден проводник, силата на полето намалява и следователно потенциалът на проводника намалява. Според уравнението това означава увеличаване на капацитета на проводника.

Кондензаторът се състои от два проводника (плочи) (фиг. 15.6), разделени от диелектричен слой. Когато определена потенциална разлика се приложи към проводник, неговите плочи се зареждат с равни заряди с противоположен знак. Електрическият капацитет на кондензатора се разбира като физическо количество, пропорционално на заряда q и обратно пропорционално на потенциалната разлика между плочите

Нека определим капацитета на плосък кондензатор.

Ако площта на плочата е S и зарядът върху нея е q, тогава силата на полето между плочите

От друга страна, потенциалната разлика между плочите идва от

Енергия на система от точкови заряди, зареден проводник и кондензатор.

Всяка система от заряди има някаква потенциална енергия на взаимодействие, която е равна на работата, изразходвана за създаването на тази система. Енергия на система от точкови заряди р 1 , р 2 , р 3 ,… р нсе определя, както следва:

Където φ 1 – потенциал на електрическото поле, създадено от всички заряди с изключение на р 1 в точката, където се намира зарядът р 1 и т.н. Ако конфигурацията на системата от заряди се промени, тогава енергията на системата също се променя. За да промените конфигурацията на системата, трябва да се работи.

Потенциалната енергия на система от точкови заряди може да се изчисли по друг начин. Потенциална енергия на два точкови заряда р 1 , р 2 на разстояние едно от друго е равно. Ако има няколко заряда, тогава потенциалната енергия на тази система от заряди може да се определи като сумата от потенциалните енергии на всички двойки заряди, които могат да бъдат съставени за тази система. И така, за система от три положителни заряда, енергията на системата е равна на

Енергия на зареден самотен проводник и кондензатор

Ако изолиран проводник има заряд q, тогава около него има електрическо поле, чийто потенциал на повърхността на проводника е равен на , а капацитетът е C. Нека увеличим заряда с количеството dq. При прехвърляне на заряд dq от безкрайност трябва да се извърши работа, равна на . Но потенциалът на електростатичното поле на даден проводник в безкрайност е нула. Тогава

При прехвърляне на заряд dq от проводник към безкрайност, същата работа се извършва от силите на електростатичното поле. Следователно, когато зарядът на проводника се увеличи с количество dq, потенциалната енергия на полето се увеличава, т.е.

Чрез интегриране на този израз намираме потенциалната енергия на електростатичното поле на зареден проводник, когато зарядът му нараства от нула до q:

Прилагайки връзката, можем да получим следните изрази за потенциалната енергия W:

Следователно за зареден кондензатор потенциалната разлика (напрежение) е равна на отношението към общата енергия на неговото електростатично поле: