Разстоянието между концентрираните товари е същото, а разстоянието от началото на участъка до първия концентриран товар е равно на разстоянието между концентрираните товари. В този случай концентрираните натоварвания също падат върху началото и края на участъка, но в същото време те само предизвикват увеличаване на опорната реакция; екстремните концентрирани натоварвания не влияят по никакъв начин на стойността на огъващите моменти и деформацията, и следователно не се вземат предвид при изчисляване на носещата способност на конструкцията. Нека разгледаме това като използваме примера за подови греди, лежащи върху преграда. Тухлената зидария, която може да бъде между преградата и гредите на пода и да създава равномерно разпределено натоварване, не е показана за по-лесно възприемане.
Снимка 1. Намаляване на концентрираните товари до еквивалентно равномерно разпределено натоварване.
Както се вижда от фигура 1, определящият момент е моментът на огъване, който се използва при изчисляване на якостта на конструкциите. По този начин, за да може едно равномерно разпределено натоварване да произведе същия момент на огъване като концентрирано натоварване, то трябва да бъде умножено по съответния коефициент на преход (коефициент на еквивалентност). И този коефициент се определя от условията за равенство на моментите. Мисля, че фигура 1 илюстрира това много добре. Също така, анализирайки получените зависимости, можем да изведем обща формулаза определяне на коефициента на преход. Така че, ако броят на приложените концентрирани товари е нечетен, т.е. едно от концентрираните натоварвания задължително пада в средата на обхвата, след което за определяне на коефициента на еквивалентност можете да използвате формулата:
γ = n/(n - 1) (305.1.1)
където n е броят на обхватите между концентрираните товари.
q eq = γ(n-1)Q/l (305.1.2)
където (n-1) е броят на концентрираните товари.
Понякога обаче е по-удобно да се правят изчисления въз основа на броя на концентрираните товари. Ако тази величина е изразена с променливата m, тогава
γ = (m +1)/m (305.1.3)
В този случай еквивалентният равномерно разпределен товар ще бъде равен на:
q eq = γmQ/l (305.1.4)
Когато броят на концентрираните товари е четен, т.е. нито едно от концентрираните товари не попада в средата на обхвата, тогава стойността на коефициента може да се приеме като за следващата нечетна стойност на броя на концентрираните товари. Като цяло, при определени условия на натоварване, могат да се приемат следните коефициенти на преход:
γ = 2- ако разглежданата конструкция, например, гредата получава само едно концентрирано натоварване в средата на преградата.
у = 1,33- за греда, подложена на 2 или 3 концентрирани натоварвания;
γ = 1,2- за греда, подложена на 4 или 5 концентрирани натоварвания;
γ = 1,142- за греда, подложена на 6 или 7 концентрирани натоварвания;
у = 1,11- за греда, подложена на 8 или 9 концентрирани натоварвания.
Вариант 2
Разстоянието между концентрираните товари е еднакво, като разстоянието от началото на участъка до първото концентрирано натоварване е равно на половината от разстоянието между концентрираните товари. В този случай концентрираните натоварвания не падат върху началото и края на участъка.
Фигура 2. Стойности на коефициентите на преход за вариант 2 на прилагане на концентрирани товари.
Както може да се види от фигура 2, с тази опция за зареждане стойността на коефициента на преход ще бъде значително по-малка. Така например, при четен брой концентрирани товари, коефициентът на преход обикновено може да се приеме равен на единица. За нечетен брой концентрирани товари формулата може да се използва за определяне на коефициента на еквивалентност:
γ = (m +7)/(m +6) (305.2.1)
където m е броят на концентрираните товари.
В този случай еквивалентният равномерно разпределен товар ще бъде равен на:
q eq = γmQ/l (305.1.4)
Като цяло, при определени условия на натоварване, могат да се приемат следните коефициенти на преход:
γ = 2- ако разглежданата конструкция, например, получава само едно концентрирано натоварване в средата на преградата и дали гредите на пода падат в началото или края на участъка или са разположени произволно далеч от началото и края на участъка, в случая няма значение. А това е важно при определяне на концентрирания товар.
γ = 1- ако въпросната конструкция е подложена на четен брой натоварвания.
у = 1,11- за греда, подложена на 3 концентрирани натоварвания;
γ = 1,091- за греда, подложена на 5 концентрирани натоварвания;
у = 1,076- за греда, подложена на 7 концентрирани натоварвания;
γ = 1,067- за греда, подложена на 9 концентрирани натоварвания.
Въпреки някои сложни определения, коефициентите на еквивалентност са много прости и удобни. Тъй като по време на изчисленията разпределеният товар, действащ на квадратен или линеен метър, много често е известен, за да не се преобразува разпределеният товар първо в концентриран товар, а след това отново в еквивалентен разпределен, е достатъчно просто да се умножи стойността на разпределен товар чрез съответния коефициент. Например таванът ще бъде подложен на стандартно разпределено натоварване от 400 kg/m2, докато собственото тегло на тавана ще бъде още 300 kg/m2. Тогава, при дължина на подовата греда от 6 m, равномерно разпределено натоварване q = 6(400 + 300)/2 = 2100 kg/m може да действа върху преградата. И тогава, ако има само една подова греда в средата на участъка, тогава γ = 2 и
q eq = γq = 2q (305.2.2)
Ако нито едно от двете условия по-горе не е изпълнено, тогава е невъзможно да се използват коефициенти на преход в тяхната чиста форма; трябва да добавите няколко допълнителни коефициента, които отчитат разстоянието до гредите, които не попадат в началото и края на обхвата на преградата, както и възможната асиметрия на прилагането на концентрирани товари. По принцип е възможно да се изведат такива коефициенти, но във всеки случай те ще бъдат намаляващи във всички случаи, ако вземем предвид първия случай на натоварване и в 50% от случаите, ако разгледаме втория случай на натоварване, т.е. стойностите на тези коефициенти ще бъдат< 1. А потому для упрощения расчетов, а заодно и для повече запасиПо отношение на якостта на изчисляваната конструкция коефициентите, дадени за първите два варианта на натоварване, са напълно достатъчни.
Разпределение на напрежението в случай на равнинна задача
Този случай съответства на напрегнатото състояние под основи на стени, подпорни стени, насипи и други конструкции, чиято дължина значително надвишава техните напречни размери:
 Където л– дължина на основата; b– ширина на основата. В този случай разпределението на напрежението под която и да е част от конструкцията, идентифицирано от две успоредни секции, перпендикулярни на оста на конструкцията, характеризира състоянието на напрежение под цялата конструкция и не зависи от координатите, перпендикулярни на посоката на натоварената равнина.
Където л– дължина на основата; b– ширина на основата. В този случай разпределението на напрежението под която и да е част от конструкцията, идентифицирано от две успоредни секции, перпендикулярни на оста на конструкцията, характеризира състоянието на напрежение под цялата конструкция и не зависи от координатите, перпендикулярни на посоката на натоварената равнина.
Нека разгледаме действието на линеен товар под формата на непрекъсната серия от концентрирани сили Р, всяка от които е на единица дължина. В този случай компонентите на напрежението във всяка точка Мс координати Ри b могат да бъдат намерени по аналогия с пространствения проблем:
 (3.27)
(3.27)
Ако връзките между геометричните характеристики на разглежданите точки z, г, bпредставени под формата на коефициенти на влияние К, тогава формулите за напрежения могат да бъдат записани, както следва:
 (3.28)
(3.28)
Стойности на коефициента на влияние K z,K y,K yzтаблично в зависимост от относителните координати з б, г/б(Таблица II.3 от Приложение II).
Важно свойство на равнинната задача е, че компонентите на напрежението Tи s гв разглежданата равнина z 0гне зависят от коефициента на напречно разширение n 0, както в случай на пространствена задача.
|

Фиг.3.15. Случайно разпределение
натоварвания на честотната лента b
Ако товарът се простира от точка А(b=b 2) до точката б(b=b 1), тогава, сумирайки напреженията от отделните му елементи, получаваме изрази за напреженията във всяка точка на масива от действието на непрекъснато ивично натоварване.
 (3.29)
(3.29)
 За равномерно разпределен товар, интегрирайте горните изрази при Py = П= конст. В този случай основните направления, т.е. посоките, в които действат най-големите и най-малките нормални напрежения, ще бъдат посоките, разположени по ъглополовящата на „ъглите на видимост“ и перпендикулярни на тях (фиг. 3.16). Ъгълът на видимост a е ъгълът, образуван от прави линии, свързващи въпросната точка Мс ленти товарни ръбове.
За равномерно разпределен товар, интегрирайте горните изрази при Py = П= конст. В този случай основните направления, т.е. посоките, в които действат най-големите и най-малките нормални напрежения, ще бъдат посоките, разположени по ъглополовящата на „ъглите на видимост“ и перпендикулярни на тях (фиг. 3.16). Ъгълът на видимост a е ъгълът, образуван от прави линии, свързващи въпросната точка Мс ленти товарни ръбове.
Получаваме стойностите на главните напрежения от изразите (3.27), като приемем b=0 в тях:
![]() . (3.30)
. (3.30)
Тези формули често се използват при оценка на напрегнатото състояние (особено граничното състояние) в основите на конструкциите.
Използвайки стойностите на главните напрежения като полуоси, е възможно да се конструират елипси на напрежение, които визуално характеризират напрегнатото състояние на почвата при равномерно разпределено натоварване, приложено по протежение на лентата. Разпределението (местоположението) на елипсите на напрежение под действието на локално равномерно разпределено натоварване при условията на равнинна задача е показано на фиг. 3.17.

Фиг.3.17. Елипси на напреженията под действието на равномерно разпределен товар в условията на равнинна задача
Използвайки формули (3.28), можем да определим s z, s yИ t yzвъв всички точки на сечението, перпендикулярно на надлъжната ос на товара. Ако свържем точки с еднакви стойности на всяко от тези количества, получаваме линии с еднакви напрежения. Фигура 3.18 показва линии на еднакви вертикални напрежения s z, наречени изобари, хоризонтални напрежения s г, наречени натиск, и тангенциални напрежения t zx, наречени смени.
Тези криви са конструирани от D.E. Polshin с помощта на методите на теорията на еластичността за натоварване, равномерно разпределено върху лента с ширина b, продължавайки безкрайно в посока, перпендикулярна на чертежа. Кривите показват, че ефектът от напреженията на натиск s zинтензитет 0,1 външно натоварване Рзасяга дълбочина от около 6 b, докато хоризонталните напрежения s yи допирателните t се разпространяват със същия интензитет 0,1 Рна много по-плитка дълбочина (1,5 - 2,0) b. Криволинейните повърхности с равни напрежения ще имат подобни очертания в случай на пространствен проблем.
Фиг.3.18. Линии на равно напрежение в линейно деформируема маса:
и за s z(изобари); b – за s г(разпространение); в за T(смяна)

Влиянието на ширината на натоварената лента влияе върху дълбочината на разпространение на напрежението. Например за основа с ширина 1 m, предаваща натоварване на интензивност към основата Р, напрежение 0,1 Рще бъде на дълбочина 6 m от основата, а за основа с ширина 2 m, със същата интензивност на натоварване, на дълбочина 12 m (фиг. 3.19). Ако в подлежащите слоеве има по-слаби почви, това може значително да повлияе на деформацията на конструкцията.
където a и b / са съответно ъглите на видимост и наклона на линията спрямо вертикалата (фиг. 3.21).
Фиг.3.21. Диаграми на разпределение на напреженията на натиск по вертикални сечения на почвен масив под действието на триъгълно натоварване
Таблица II.4 от Приложение II показва зависимостите на коефициента ДА СЕ| z в зависимост от z/bИ г/b(Фиг. 3.21), за да изчислите s z по формулата:
s z = ДА СЕ| z × Р.
При инженерните изчисления често се срещат товари, разпределени по дадена повърхност според един или друг закон. Нека разгледаме някои прости примери за разпределени сили, лежащи в една и съща равнина.
Плоска система от разпределени сили се характеризира с нейния интензитет q, т.е. стойността на силата на единица дължина на натоварения сегмент. Интензитетът се измерва в нютони, разделени на метри

1) Силите, равномерно разпределени по права линия (фиг. 69, а). За такава система от сили интензитетът q има постоянна стойност. При статични изчисления тази система от сили може да бъде заменена с резултантната
Модуло,
Силата Q се прилага в средата на сегмент AB.
2) Силите, разпределени по прав сегмент по линеен закон (фиг. 69, b). Пример за такова натоварване могат да бъдат силите на водното налягане върху язовир, имащ най-висока стойностна дъното и пада до нула на повърхността на водата. За тези сили интензитетът q е променлива стойност, нарастваща от нула до максимална стойностРезултантната Q на такива сили се определя подобно на резултантната на гравитационните сили, действащи върху хомогенна триъгълна плоча ABC. Тъй като теглото на хомогенна плоча е пропорционално на нейната площ, тогава по модул,
Силата Q се прилага на разстояние от страната BC на триъгълник ABC (вижте § 35, параграф 2).
3) Силите, разпределени по права линия по произволен закон (фиг. 69, c). Резултантната Q на такива сили, по аналогия със силата на гравитацията, е равна по големина на площта на фигурата ABDE, измерена в подходяща скала, и преминава през центъра на тежестта на тази област (въпросът за определяне центровете на тежестта на площите ще бъдат обсъдени в § 33).
4) Силите, равномерно разпределени по дъгата на окръжност (фиг. 70). Пример за такива сили са силите на хидростатично налягане върху страничните стени на цилиндричен съд.
Нека радиусът на дъгата е равен на , където е оста на симетрия, по която насочваме оста Системата от събиращи се сили, действащи върху дъгата, има резултатна Q, насочена поради симетрия по оста и числено

За да определим стойността на Q, избираме елемент върху дъгата, чиято позиция се определя от ъгъла и дължината на силата, действаща върху този елемент, е числено равна и проекцията на тази сила върху оста ще бъде Тогава
Но от фиг. 70 е ясно, че Следователно от тогава
където е дължината на хордата, обхващаща дъгата AB; q - интензитет.

Задача 27. Равномерно разпределено натоварване с интензитет действа върху конзолна греда A B, чиито размери са посочени на чертежа (фиг. 71). Пренебрегвайки теглото на гредата и приемайки, че силите на натиск върху вградения край се определят съгласно към линеен закон, определете стойностите на най-високите интензитети на тези сили, Ако
Решение. Заменяме разпределените сили с техните резултанти Q, R и R, където съгласно формули (35) и (36)
и съставете условия на равновесие (33) за паралелни сили, действащи върху гредата
Замествайки тук вместо Q, R и R техните стойности и решавайки получените уравнения, най-накрая ще намерим
Например кога получаваме и кога
Задача 28. Цилиндричен цилиндър с височина H и вътрешен диаметър d е напълнен с газ под налягане.Дебелината на цилиндричните стени на цилиндъра е a. Определете напреженията на опън, изпитвани от тези стени в посоки: 1) надлъжно и 2) напречно (напрежението е равно на съотношението на силата на опън към площта на напречното сечение), считайки го за малко.
Решение. 1) Нека разрежем цилиндъра на две части с равнина, перпендикулярна на неговата ос, и разгледаме равновесието на една от тях (фиг.
72, а). Върху него по посока на оста на цилиндъра действа силата на натиск върху дъното и силите, разпределени върху площта на напречното сечение (действието на изхвърлената половина), чийто резултат ще бъде означен с Q. При равновесие
Ако приемем, че площта на напречното сечение е приблизително еднаква, получаваме стойността за напрежението на опън
Всеки собственик на трифазен вход (380 V) е длъжен да се грижи за равномерно натоварване на фазите, за да избегне претоварване на една от тях. Ако има неравномерно разпределение на трифазния вход, ако нулата изгори или лошият й контакт, напреженията на фазовите проводници започват да се различават едно от друго, както нагоре, така и надолу. При еднофазно ниво на мощност (220 волта) това може да доведе до повреда на електрическите уреди поради повишено напрежение от 250-280 волта или намалено напрежение от 180-150 волта. Освен това в този случай има повишена консумация на електроенергия в електрически уреди, които не са чувствителни към дисбаланси на напрежението. В тази статия ще ви разкажем как натоварването се разпределя между фазите, предоставяйки кратки инструкции с диаграма и видео пример.
Какво е важно да знаете
Тази диаграма грубо илюстрира трифазна мрежа:
Напрежението между фазите от 380 волта е посочено в синьо. Зеленият цвят показва равномерно разпределено мрежово напрежение. Червено - дисбаланс на напрежението.
Новите абонати на трифазно електричество в частна къща или апартамент, когато се свързват за първи път, не трябва да имат много надежда за първоначално равномерно разпределено натоварване на входната линия. Тъй като няколко потребителя могат да се захранват от една линия и те могат да имат проблеми с разпределението.
Ако след измерванията видите, че има (повече от 10%, съгласно GOST 29322-92), трябва да се свържете с електроснабдителната организация, за да предприемете подходящи мерки за възстановяване на фазовата симетрия. Можете да научите повече за това от нашата статия.
Съгласно договора между абоната и ВЕИ (за използване на електроенергия), последният трябва да доставя висококачествена електроенергия на домовете, с посочените . Честотата също трябва да съответства на 50 Hz.
Правила за разпространение
При проектирането на електрическа схема е необходимо да се изберат предвидените потребителски групи възможно най-равномерно и да се разпределят между фазите. Например, всяка група гнезда в стаи в къщата е свързана към собствен фазов проводник и групирана по такъв начин, че натоварването на мрежата да е оптимално. Осветителните линии са организирани по същия начин, разпределяйки ги между различни фазови проводници и т.н.: пералня, печка, фурна, котел, бойлер.


Наред с концентрираните сили, обсъдени по-горе, могат да бъдат изложени на строителни конструкции и конструкции разпределени товари– по обем, по повърхност или по определена линия – и се определя от нея интензивност.
Пример за товар разпределени по площ, е натоварването от сняг, налягането на вятъра, налягането на течността или налягането на почвата. Интензитетът на такова повърхностно натоварване има размерността на налягането и се измерва в kN/m2 или килопаскали (kPa = kN/m2).
При решаването на проблеми често има натоварване, което разпределени по дължината на гредата. Интензивност ртакова натоварване се измерва в kN/m.
Помислете за греда, натоварена върху сечението [ а, b] разпределено натоварване, чиято интензивност варира според закона р= р(х). За да се определят опорните реакции на такава греда, е необходимо разпределеното натоварване да се замени с еквивалентно концентрирано. Това може да стане съгласно следното правило:
Нека разгледаме специални случаи на разпределено натоварване.
а) общ случай на разпределен товар(фиг.24)
Фиг.24
q(x) - интензитет на разпределената сила [N/m],
Елементарна сила.
л– дължина на сегмента
Силата на интензитет q(x), разпределена по прав сегмент, е еквивалентна на концентрирана сила
Концентрирана сила се прилага в точка СЪС(център на успоредни сили) с координат
![]()
б) постоянен разпределен интензитет на натоварване(фиг.25)

Фиг.25
![]()
![]()
V) разпределен интензитет на натоварване, вариращ линейно(фиг.26)

Фиг.26
![]()
![]()
Изчисляване на композитни системи.
Под композитни системи Ще разберем структури, състоящи се от няколко тела, свързани помежду си.
Преди да преминем към разглеждане на характеристиките на изчислението на такива системи, въвеждаме следното определение.
Статично определимиТова са проблеми и системи от статика, за които броят на неизвестните реакции на ограниченията не надвишава максимално допустимия брой уравнения.
Ако броят на неизвестните е по-голям от броя на уравненията,релевантни се наричат задачи и системи статически неопределени. В този случай се извиква разликата между броя на неизвестните и броя на уравненията степен на статична неопределеностсистеми.
За всяка плоска система от сили, действащи върху твърдо тяло, има три независими условия на равновесие. Следователно за всяка равнинна система от сили от равновесни условия могат да се намерят не повече от три неизвестни реакции на свързване.
В случай на пространствена система от сили, действащи върху твърдо тяло, има шест независими условия на равновесие. Следователно за всяка пространствена система от сили от равновесни условия могат да се намерят не повече от шест неизвестни реакции на свързване.
Нека обясним това със следните примери.
1. Нека центърът на безтегловен идеален блок (пример 4) се държи не от два, а от три пръта: AB, слънцеИ BDи е необходимо да се определят реакциите на прътите, като се пренебрегват размерите на блока.
Като вземем предвид условията на проблема, получаваме система от сближаващи се сили, където да определим три неизвестни: S A, S CИ S Dвсе още е възможно да се състави система само от две уравнения: Σ х = 0, Σ Y=0. Очевидно поставеният проблем и съответната система ще бъдат статически неопределени.
2. Греда, здраво закрепена в левия край и имаща шарнирно фиксирана опора в десния край, се натоварва с произволна равнинна система от сили (фиг. 27).
За да определите опорните реакции, можете да създадете само три равновесни уравнения, които ще включват 5 неизвестни опорни реакции: X A, Y A,М А,X БИ Y B. Посочената задача ще бъде два пъти статично неопределена.
Подобен проблем не може да бъде решен в рамките на теоретичната механика, приемайки въпросното тяло за абсолютно твърдо.

Фиг.27
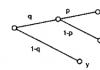
Нека се върнем към изучаването на композитни системи, типичен представител на които е рамка с три панти (фиг. 28, А). Състои се от две тела: A.C.И пр.н.е., свързан ключпанта ° С. Използвайки тази рамка като пример, помислете два начина за определяне на опорните реакции на композитните системи.
1 начин.Помислете за тялото A.C., натоварени с дадена сила Р, отхвърляйки всички връзки в съответствие с аксиома 7 и заменяйки ги съответно с външни реакции ( X А, У А) и вътрешни ( X C, YC) връзки (фиг. 28, b).
По същия начин можем да разгледаме баланса на тялото пр.н.е.под влияние на опорни реакции IN - (X Б, Y B) и реакции в съединителната става ° С - (X C', YC“), където в съответствие с аксиома 5: X C= X C', YC= YC’.
По този начин за всяко от тези тела могат да бъдат съставени три уравнения на равновесие общ бройнеизвестен: X А, У А , X C=X C', YC =YC’, X Б, Y Bе равен на общия брой уравнения и проблемът е статично определим.
Нека припомним, че според условията на задачата беше необходимо да се определят само 4 опорни реакции, но трябваше да свършим допълнителна работа, като определим реакциите в свързващата панта. Това е недостатъкът на този метод за определяне на опорните реакции.
Метод 2.Помислете за баланса на цялата рамка ABC, отхвърляйки само външни връзки и заменяйки ги с неизвестни реакции на поддръжка X А, У А,X Б, Y B .
Получената система се състои от две тела и не е абсолютно твърдо тяло, тъй като разстоянието между точките АИ INможе да се промени поради взаимно завъртане на двете части спрямо пантата СЪС. Въпреки това можем да приемем, че съвкупността от сили, приложени към рамката ABCобразува система, ако използваме аксиомата за втвърдяване (фиг. 28, V).

Фиг.28
Така че за тялото ABCмогат да се съставят три равновесни уравнения. Например:
Σ М А = 0;
Σ х = 0;
Тези три уравнения ще включват 4 неизвестни опорни реакции X А, У А,X БИ Y B. Имайте предвид, че опит да се използва, например, това като липсващо уравнение: Σ М В= 0 няма да доведе до успех, тъй като това уравнение ще бъде линейно зависимо от предишните. За да се получи линейно независимо четвърто уравнение, е необходимо да се вземе предвид равновесието на друго тяло. Като него можете да вземете една от частите на рамката, например - слънце. В този случай трябва да създадете уравнение, което да съдържа „старите“ неизвестни X А, У А,X Б, Y Bи не съдържа нови. Например уравнението: Σ х (слънце) = 0 или повече подробности: - X C ' + X Б= 0 не е подходящ за тези цели, тъй като съдържа „ново“ неизвестно X C“, но тук е уравнението Σ М С (слънце) = 0 отговаря на всички необходими условия. По този начин необходимите опорни реакции могат да бъдат намерени в следната последователност:
Σ М А = 0; → Y B= Р/4;
Σ М В = 0; → У А= -Р/4;
Σ М С (слънце) = 0; → X Б= -Р/4;
Σ х = 0; →X А= -3Р/4.
За да проверите, можете да използвате уравнението: Σ М С (AC) = 0 или по-подробно: - У А∙2 + X А∙2 + Р∙1 = Р/4∙2 -3Р/4∙2 +Р∙1 = Р/2 - 3Р/2 +Р = 0.
Имайте предвид, че това уравнение включва всички 4 открити опорни реакции: X АИ У А- в изрична форма и X БИ Y B- имплицитни, тъй като те са използвани за определяне на първите две реакции.
Графично определяне на опорните реакции.
В много случаи решаването на проблеми може да бъде опростено, ако вместо уравнения на равновесие или в допълнение към тях директно се използват условия на равновесие, аксиоми и теореми на статиката. Съответният подход се нарича графично определяне на опорните реакции.
Преди да преминем към разглеждане на графичния метод, отбелязваме, че що се отнася до система от сближаващи се сили, само онези проблеми, които могат да бъдат решени аналитично, могат да бъдат решени графично. В същото време графичният метод за определяне на опорните реакции е удобен за малък брой товари.
И така, графичният метод за определяне на опорните реакции се основава главно на използването на:
Аксиоми за равновесието на система от две сили;
Аксиоми за действие и реакция;
Три силови теореми;
Условия на равновесие за плоска система от сили.
При графично определяне на реакциите на композитни системи се препоръчва следното: последователност на разглеждане:
Изберете тяло с минимален брой алгебрични неизвестни реакции на свързване;
Ако има две или повече такива тела, тогава започнете решението, като разгледате тялото, към което са приложени по-малко сили;
Ако има две или повече такива тела, тогава изберете тялото, за което по-голям бройсилите се познават по посока.
Разрешаване на проблем.
Когато решавате проблемите от този раздел, трябва да имате предвид всички общи инструкции, направени по-рано.
При започване на решаването е необходимо преди всичко да се установи равновесието на кое конкретно тяло трябва да се вземе предвид в този проблем. След това, изолирайки това тяло и го считайки за свободно, трябва да изобразите всички дадени сили и реакции на изхвърлени връзки, действащи върху тялото.
След това трябва да създадете условия за равновесие, като приложите формата на тези условия, която води до по-проста система от уравнения (най-простата система ще бъде система от уравнения, всяко от които включва едно неизвестно).
За да получите по-прости уравнения, трябва (освен ако това не усложнява изчислението):
1) когато съставяте проекционни уравнения, начертайте координатната ос, перпендикулярна на някаква неизвестна сила;
2) когато съставяте моментно уравнение, препоръчително е да изберете като моментна точка точката, в която се пресичат линиите на действие на две от трите неизвестни опорни реакции - в този случай те няма да бъдат включени в уравнението и то ще съдържа само едно неизвестно;
3) ако две от трите неизвестни опорни реакции са успоредни, тогава при изготвяне на уравнение в проекции върху оста, последната трябва да бъде насочена така, че да е перпендикулярна на първите две реакции - в този случай уравнението ще съдържа само последното неизвестно;
4) при решаване на задача координатната система трябва да бъде избрана така, че нейните оси да са ориентирани по същия начин като по-голямата част от силите на системата, приложени към тялото.
Когато се изчисляват моментите, понякога е удобно да се разложи дадена сила на два компонента и, като се използва теоремата на Varignon, да се намери моментът на силата като сума от моментите на тези компоненти.
Решаването на много задачи по статиката се свежда до определяне на реакциите на опорите, с които се закрепват греди, мостови ферми и др.
Пример 7.Към скобата, показана на фиг. 29, а,на възела INе окачен товар с тегло 36 kN. Връзките на елементите на скобата са шарнирни. Определете силите, възникващи в прътите ABИ слънце, считайки ги за безтегловни.
Решение.Помислете за равновесието на възела IN, където се срещат пръчките ABИ слънце. Възел INпредставлява точка на чертежа. Тъй като товарът е спрян от възела IN, след това в точката INприложете сила F, равна на теглото на окачения товар. пръти ВирджинияИ слънце, шарнирно свързани във възел IN,ограничават възможността за всяко линейно движение във вертикалната равнина, т.е. са връзки по отношение на възела IN.

Ориз. 29.Изчислителна схема на скобата за пример 7:
А -схема за проектиране; б –система от сили във възел б
Мислено отхвърлете връзките и заменете техните действия със сили - реакции на връзките Р АИ R C. Тъй като прътите са безтегловни, реакциите на тези пръти (силите в прътите) са насочени по оста на прътите. Да приемем, че и двата пръта са опънати, т.е. техните реакции са насочени от шарнира към прътите. Тогава, ако след изчисление реакцията се окаже със знак минус, това ще означава, че всъщност реакцията е насочена в посока, обратна на тази, посочена на чертежа, т.е. прътът ще бъде компресиран.
На фиг. 29, bе показано, че в точката INприложена активна сила Еи реакциите на връзките Р АИ Р С.Вижда се, че изобразената система от сили представлява плоска система от сили, събиращи се в една точка. Избираме произволни координатни оси ОХИ ойи съставете уравнения на равновесие от вида:
Σ F x = 0;-R a - R c cos𝛼 = 0;
Σ F y = 0; -F - R c cos(90 - α) = 0.
Като се има предвид това защото (90 -α ) = гряхα, от второто уравнение намираме
Rc = -F/sinα = - 36/0,5 = -72 kN.
Заместване на стойността Rcв първото уравнение, получаваме
Ra = -R c cosα= - (-72) ∙0,866 = 62,35 kN.
По този начин прътът AB- опъната, и пръчката слънце- компресиран.
За да проверим правилността на намерените сили в прътите, проектираме всички сили върху всяка ос, която не съвпада с осите хИ Y, например, ос U:
Σ F u = 0; -R c - R a cosα -Fcos(90- α) = 0.
След като заместим стойностите на намерените сили в прътите (размер в килонютони), получаваме
- (-72) – 62,35∙0,866 - 36∙0,5 = 0; 0 = 0.
Условието за равновесие е изпълнено, следователно намерените сили в прътите са правилни.
Пример 8.Гредата на строително скеле, чието тегло може да се пренебрегне, се държи в хоризонтално положение от гъвкав прът CDи шарнирно лежи на стената в точка А. Намерете силата на тягата CD, ако работник с тегло 80 kg стои на ръба на скелето ≈0,8 kN (фиг. 30, А).

Ориз. тридесет.Проектна схема на скеле за пример 8:
А– проектна схема; b– система от сили, действащи върху скелето
Решение.Избираме обекта на равновесие. В този пример обектът на равновесие е гредата на скелето. В точката INвърху гредата действа активна сила Е, равно на теглото на човек. Връзките в този случай са фиксирана опорна панта Аи сцепление CD. Нека изхвърлим мислено връзките, като заменим тяхното действие върху лъча с реакциите на връзките (фиг. 30, b). Не е необходимо да се определя реакцията на фиксирана шарнирна опора според условията на проблема. Реакция в тягата CDнасочен по протежение на тягата. Да приемем, че прътът CDопъната, т.е. реакция Р Днасочена встрани от пантата СЪСвътре в пръта. Нека разбием реакцията Р Д, съгласно правилото на успоредника, на хоризонтални и вертикални компоненти:
R Dx планини =R D cosα ;
R Dy vert = R D cos(90-α) = R D гряхα .
В резултат на това получихме произволна плоска система от сили, необходимо условиеравновесието на което е равенство на нула на три независими условия на равновесие.
В нашия случай е удобно първо да запишете условието за равновесие под формата на сума от моменти спрямо моментната точка А, от момента на реакцията на поддръжката Р Аспрямо тази точка е нула:
Σ м А = 0; Е∙3а - Р dy∙ а = 0
Е∙3а - R D гряхα = 0.
Значение тригонометрични функцииопредели от триъгълника ACD:
cosα = AC/CD = 0,89,
sinα = AD/CD = 0,446.
Решавайки уравнението на равновесието, получаваме Р D = 5,38 kN. (Пътуване CD- разтегнат).
За да проверите правилността на изчисляване на силата в шнура CDнеобходимо е да се изчисли поне един от компонентите на опорната реакция Р А. Нека използваме уравнението на равновесието във формата
Σ Fy = 0; V A + R Dy- Е= 0
V A = Е- Rdy.
Оттук V A= -1,6 kN.
Знакът минус означава, че вертикалният компонент на реакцията Р Авърху опората е насочена надолу.
Нека проверим правилността на изчисляването на силата в шнура. Използваме друго условие за равновесие под формата на уравнения на моменти около точката IN.
Σ m В = 0; V A∙3a + R Dy ∙ 2а = 0;
1,6∙3А + 5,38∙0,446∙2А = 0; 0 = 0.
Условията за равновесие са изпълнени, така че силата в нишката се намира правилно.
Пример 9.Вертикалният бетонен стълб се бетонира с долния си край в хоризонтална основа. Натоварване от стената на сградата с тегло 143 kN се предава на стълба отгоре. Стълбът е от бетон с плътност γ = 25 kN/m3. Размерите на стълба са показани на фиг. 31, А. Определяне на реакциите при твърдо вграждане.

Ориз. 31.Изчислителна схема на стълба за пример 9:
А– схема на натоварване и размери на стълба; b– проектна схема
Решение.В този пример обектът на равновесие е стълб. Колоната е натоварена със следните видове активни натоварвания: в точката Аконцентрирана сила F, равна на теглото на стената на сградата и собственото тегло на колоната под формата на интензитет на натоварване, равномерно разпределен по дължината на гредата рза всеки метър дължина на стълба: q = 𝛾A, Където А- площ на напречното сечение на колоната.
р= 25∙0,51∙0,51 = 6,5 kN/m.
Връзките в този пример са твърдото вграждане в основата на стълба. Нека мислено да изхвърлим уплътнението и да заменим действието му с реакции на връзки (фиг. 31, b).
В нашия пример разглеждаме специален случай на действие на система от сили, перпендикулярни на вграждането и преминаващи по една ос през точката на прилагане на опорните реакции. Тогава две опорни реакции: хоризонталната компонента и реактивният момент ще бъдат равни на нула. За да определим вертикалния компонент на опорната реакция, проектираме всички сили върху оста на елемента. Нека подравним тази ос с оста Z,тогава условието за равновесие ще бъде записано като следната форма:
Σ Ф З = 0; V B - F - ql = 0,
Където ql- резултатна от разпределения товар.
V Б = F+ql= 143 + 6,5∙4 = 169 kN.
Знакът плюс показва, че реакцията V Бнасочени нагоре.
За да се провери правилността на изчислението на опорната реакция, остава още едно условие за равновесие - под формата на алгебрична сума на моментите на всички сили спрямо всяка точка, която не минава през оста на елемента. Предлагаме ви да извършите тази проверка сами.
Пример 10.За гредата, показана на фиг. 32, А, е необходимо да се определят опорните реакции. дадени: Е= 60 kN, р= 24 kN/m, М= 28 kN∙m.

Ориз. 32.Проектна схема и размери на гредата за пример 10:
Решение.Помислете за равновесието на лъч. Гредата е натоварена с активно натоварване под формата на плоска система от успоредни вертикални сили, състояща се от концентрирана сила Е, равномерно разпределен интензитет на натоварване рс резултат Q, приложен в центъра на тежестта на товарното пространство (фиг. 32, b), и концентриран момент М, което може да се представи като двойка сили.
Връзките в тази греда са шарнирно фиксирана опора Аи съчленена подвижна опора IN. Нека подчертаем обекта на равновесие; за да направим това, ще изхвърлим поддържащите връзки и ще заменим техните действия с реакции в тези връзки (фиг. 32, b). Реакция на движещата се опора Р Бе насочена вертикално, а реакцията на шарнирно-неподвижната опора Р Аще бъде успоредна на активната система от действащи сили и също насочена вертикално. Да приемем, че сочат нагоре. Резултат от разпределения товар Q= 4,8∙q се прилага в центъра на симетрия на товарното пространство.
При определяне на опорните реакции в гредите е необходимо да се стремим да конструираме уравнения на равновесие по такъв начин, че всяко от тях да включва само едно неизвестно. Това може да се постигне чрез конструиране на две моментни уравнения относно референтните точки. Опорните реакции обикновено се проверяват чрез съставяне на уравнение под формата на сумата от проекциите на всички сили върху ос, перпендикулярна на оста на елемента.
Нека условно приемем посоката на въртене на момента на опорните реакции около моментните точки за положителна, тогава обратната посока на въртене на силите ще се счита за отрицателна.
Необходимо и достатъчно условие за равновесие в този случай е равенството на нула на независимите условия на равновесие във вида:
Σ м А = 0; V Б ∙6 - р∙4,8∙4,8 + М+Ж∙2,4 = 0;
Σ м Б = 0; V A∙6 - р∙4,8∙1,2 - М - Е∙8,4 = 0.
Замествайки числените стойности на количествата, намираме
V Б= 14,4 kN, V A= 15,6 kN.
За да проверим правилността на откритите реакции, използваме условието за равновесие във формата:
Σ Fy = 0; V A + V B - F -q∙4,8 =0.
След като заместим числените стойности в това уравнение, получаваме идентичност от типа 0=0. От тук заключаваме, че изчислението е извършено правилно и реакциите и на двете опори са насочени нагоре.
Пример 11.Определете опорните реакции за гредата, показана на фиг. 33, А. дадени: Е= 2,4 kN, М= 12 kN∙m, р= 0,6 kN/m, a = 60°.

Ориз. 33.Проектна схема и размери на гредата за пример 11:
а – проектна диаграма; b – обект на равновесие
Решение.Помислете за равновесието на лъч. Мислено освободете гредата от връзките на опорите и изберете обекта на баланс (фиг. 33, b). Гредата е натоварена с активен товар под формата на произволна равнинна система от сили. Резултат от разпределения товар Q = р∙3 е прикрепен към центъра на симетрия на товарното пространство. Сила ЕНека разложим успоредника на компоненти - хоризонтална и вертикална - по правилото на успоредника.
F z = F cosα= 2,4 cos 60°= 1,2 kN;
F y = F cos(90-α) = Егрях 60°= 2,08 kN.
Ние прилагаме реакции към равновесния обект вместо изхвърлени връзки. Да предположим вертикална реакция V Aсъчленена опора Анагоре, вертикална реакция V Бсъчленена фиксирана опора бсъщо е насочена нагоре и хоризонталната реакция H B- надясно.
Така на фиг. 33, bизобразява произволна равнинна система от сили, необходимото условие за равновесие на която е равенството на нула на три независими условия на равновесие за равнинна система от сили. Спомнете си, че според теоремата на Вариньон моментът на силата Еспрямо всяка точка е равна на сумата от моментите на компонентите F z и F yспрямо същата точка. Нека условно приемем посоката на въртене на момента на опорните реакции около моментните точки за положителна, тогава обратната посока на въртене на силите ще се счита за отрицателна.
Тогава е удобно условията на равновесие да се формулират в следната форма:
Σ Fz = 0; - F z + H B= 0; оттук H B= 1,2 kN;
Σ м А = 0; V Б∙6 + М - Fy∙2 + 3р∙0,5 = 0; оттук V Б= - 1,456 kN;
Σ м Б = 0; V A ∙6 - 3р∙6,5 - Fy ∙4 - М= 0; оттук V A= 5,336 kN.
За да проверим правилността на изчислените реакции, използваме още едно условие за равновесие, което не е използвано, например:
Σ Fy = 0; V A + V B - 3р - Fy = 0.
Вертикална опорна реакция V Бобърнат със знак минус, това показва, че в този лъч той е насочен не нагоре, а надолу.
Пример 12.Определете опорните реакции за греда, неподвижно закрепена от едната страна и показана на фиг. 34, А. дадени: р=20 kN/m.

Ориз. 34.Проектна схема и размери на гредата за пример 12:
а – проектна диаграма; b – обект на равновесие
Решение.Нека изберем обекта на равновесие. Гредата е натоварена с активен товар под формата на плоска система от успоредни сили, разположени вертикално. Мислено освободете гредата от връзките във вграждането и ги заменете с реакции под формата на концентрирана сила V Би двойки сили с желания реактивен момент М Б(виж Фиг. 34, b). Тъй като активните сили действат само във вертикална посока, хоризонталната реакция H Bравно на нула. Нека условно приемем посоката на въртене на момента на опорните реакции около моментните точки по посока на часовниковата стрелка за положителна, тогава обратната посока на въртене на силите ще се счита за отрицателна.
Съставяме условията на равновесие във формата
Σ Fy = 0; V Б- р∙1,6 = 0;
Σ м Б = 0; М Б - р∙1,6∙1,2 = 0.
Тук р∙1.6 – равностойна на разпределения товар.
Заместване на числените стойности на разпределения товар р, намираме
V V= 32 kN, М Б= 38,4 kN∙m.
За да проверим правилността на намерените реакции, нека създадем друго условие за равновесие. Сега нека вземем друга точка като моментна точка, например десния край на гредата, след което:
Σ м А = 0; М Б – V Б∙2 + р∙1,6∙0,8 = 0 .
След заместване на числовите стойности получаваме тъждеството 0=0.
Най-накрая заключаваме, че реакциите на поддръжката са намерени правилно. Вертикална реакция V Бе насочен нагоре, а реактивният момент М В- по часовниковата стрелка.
Пример 13.Определете опорните реакции на гредата (фиг. 35, А).
Решение.Активният товар е резултат от разпределения товар Q=(1/2)∙aq=(1/2)∙3∙2=3kN, чиято линия на действие минава на разстояние 1 m от лявата опора, силата на опън на нишката T = Р= 2 kN, приложено в десния край на гредата и концентриран момент.
Тъй като последното може да бъде заменено от двойка вертикални сили, натоварването, действащо върху гредата, заедно с реакцията на подвижната опора INобразува система от успоредни сили, така че реакцията Р Асъщо ще бъдат насочени вертикално (фиг. 35, b).
За да определим тези реакции, използваме уравнения за равновесие.
Σ М А = 0; -Q∙1 + Р Б∙3 - М + T∙5 = 0,
Р Б = (1/3) (Q + М-Р∙5) = (1/3) (3 + 4 - 2∙5) = -1 kN.
Σ М Б = 0; - Р А∙3 +Q∙2 - М+ T∙2 = 0,
Р А= (1/3) (Q∙2 - М+Р∙2) = (1/3) (3∙2 - 4 + 2∙2) = 2 kN.

Фиг.35
За да проверим правилността на полученото решение, използваме допълнително уравнение за равновесие:
Σ Y i = Р А - Q + Р Б+T = 2 - 3 - 1 + 2 = 0,
това означава, че проблемът е решен правилно.
Пример 14.Намерете опорните реакции на конзолната греда, натоварена с разпределен товар (фиг. 36, А).
Решение.Резултатът от разпределеното натоварване се прилага в центъра на тежестта на диаграмата на натоварването. За да не търсим позицията на центъра на тежестта на трапеца, нека си го представим като сбор от два триъгълника. Тогава даденото натоварване ще бъде еквивалентно на две сили: Q 1 = (1/2)∙3∙2 = 3 kN и Q 2 = (1/2)∙3∙4 = 6 kN, които се прилагат в центъра на тежестта на всеки от триъгълниците (фиг. 36, b).

Фиг.36
Опорните реакции на твърдото прищипване са представени чрез силата Р Аи момента М А, за да определите кое е по-удобно да използвате уравненията на равновесието на система от успоредни сили, тоест:
Σ М А = 0; М А= 15 kN∙m;
Σ Y= 0, Р А= 9 kN.
За проверка използваме допълнителното уравнение Σ М В= 0, където точка INразположен в десния край на гредата:
Σ М В = М А - Р А∙3 + Q 1 ∙2 + Q 2 ∙1 = 15 - 27 + 6 +6 = 0.
Пример 15.Претегляне на хомогенен лъч Q= 600 N и дължина л= 4 m лежи в единия край на гладък под, а в междинна точка INна височина на стълба ч= 3 m, сключваща с вертикалата ъгъл 30°. В това положение гредата се държи от опънато през пода въже. Определете напрежението на въжето Tи колонни реакции - Р Би пол - Р А(Фиг. 37, А).
Решение.Под греда или прът в теоретична механикаразбирайте тяло, чиито напречни размери в сравнение с дължината му могат да бъдат пренебрегнати. Така че теглото Qхомогенен лъч се прилага в точка СЪС, Където AC= 2 м.

Фиг.37
1) Тъй като две от трите неизвестни реакции се прилагат в точката А, първата стъпка е да се създаде уравнението Σ М А= 0, тъй като само реакцията ще отиде там Р Б:
- Р Б∙AB+Q∙(л/2)∙sin30° = 0,
Където AB = ч/cos30°= 2 m.
Замествайки в уравнението, получаваме:
Р Б∙2 = 600∙2∙(1/2) = 600,
Р Б= 600/ (2) = 100 ≅ 173 N.
По същия начин, от моментното уравнение може да се намери реакцията Р А, избирайки като моментна точка точката, в която се пресичат линиите на действие Р БИ T. Това обаче ще изисква допълнителни конструкции, така че е по-лесно да се използват други уравнения на равновесие:
2) Σ х = 0; Р Б∙cos30° - T = 0; → T = Р Б∙cos30°= 100 ∙( /2) = 150 N;
3) Σ Y= 0, Р Б∙sin30°- Q +Р А= 0; → Р А = Q- Р Б∙sin30°= 600 - 50 ≅ 513 N.
Така открихме TИ Р Апрез Р Б, следователно можете да проверите правилността на полученото решение, като използвате уравнението: Σ М Б= 0, което ще включва всички открити реакции, изрично или имплицитно:
Р А∙AB sin30°- T∙AB cos30° - Q∙(AB - л/2)∙sin30°= 513∙2 ∙(1/2) - 150∙2 ∙( /2) - 600∙ (2 - 2)∙(1/2) = 513∙ - 150∙3 - 600∙( -1) ≅ 513∙1,73 - 450 - 600∙0,73 = 887,5 - 888 = -0,5.
Получава се в резултат на закръгляване остатъчен∆= -0,5 се нарича абсолютна грешкаизчисления.
За да отговорите на въпроса колко точен е полученият резултат, изчислете относителна грешка, което се определя по формулата:
ε=[|∆| / min(|Σ + |, |Σ - |)]∙100% =[|-0,5| / мин(|887,5|, |-888|)]∙100% = (0,5/887,5)∙100% = 0,06%.
Пример 16.Определете опорните реакции на рамката (фиг. 38). Тук и по-нататък, освен ако не е посочено друго, всички размери на фигурите ще се разглеждат в метри, а силите - в килонютони.

Фиг.38
Решение.Нека разгледаме равновесието на рамка, към която се прилага силата на опън на нишката като активна сила T, равно на теглото на товара Q.
1) Реакция на подвижната опора Р Бнамираме от уравнението Σ М А= 0. За да не се изчислява лостът на силата T, ще използваме теоремата на Varignon, разлагайки тази сила на хоризонтални и вертикални компоненти:
Р Б∙2 + T sin30°∙3 - T cos30°∙4 = 0; → Р Б = (1/2)∙ Q(cos30°∙4 - sin30°∙3) = (5/4) ∙ (4 - 3) kN.
2) Да се изчисли У Анека създадем уравнение Σ М С= 0, където точка СЪСсе намира в пресечната точка на линиите на действие на реакцията Р БИ X А:
- У А∙2 + T sin30°∙3 - T cos30°∙2 = 0; → У А= (1/2)∙ Q(sin30°∙3 -cos30°∙2) = (5/4) ∙ (3 -2) kN.
3) Накрая намираме реакцията X А:
Σ х = 0; X А - T sin30° = 0; → X А =Q sin30° = 5/2 kN.
Тъй като и трите реакции са открити независимо една от друга, за да проверите, трябва да вземете уравнението, което включва всяка от тях:
Σ М Д = X А∙3 - У А∙4 - Р Б∙2 = 15/2 - 5∙(3 -2 ) - (5/2)∙ (4 - 3) = 15/2 - 15 + 10 -10 +15/2 = 0.
Пример 17.Определете опорните реакции на прът с начупен контур (фиг. 39, А).
Решение.Заменяме разпределеното натоварване върху всяка секция на пръта с концентрирани сили Q 1 = 5 kN и Q 2 = 3 kN, а действието на отхвърленото твърдо прищипване е реакция X А,У АИ М А(фиг. 39, b).

Фиг.39
1) Σ М А = 0; М А -Q 1 ∙2,5 - Q 2 ∙5,5 = 0; → М А= 5∙2,5 + 3∙5,5 = 12,5 + 16,5 = 29 kNm.
2) Σ х = 0; X А + Q 1 ∙sina = 0; → X А= -5∙(3/5) = -3 kN.
3) Σ Y= 0; У А - Q 1 коза - Q 2 = 0; →У А= 5∙(4/5) + 3 = 4 + 3 = 7 kN, тъй като sinα = 3/5, cosα = 4/5.
Проверка: Σ М В = 0; М А + X А∙3 - У А∙7 +Q 1 cosα∙4,5 + Q 1 sinα∙1,5 + Q 2 ∙1,5 = 29 -3∙3 - 7∙7 + 5∙(4/5)∙5 + 5∙(3/5)∙1,5 + 3∙1,5 = 29 - 9 - 49 + 20 + 4,5 + 4,5 = 58 - 58 = 0.
Пример 18.За рамката, показана на фиг. 40, а,необходимо е да се определят опорните реакции. дадени: Е= 50 kN, М= 60 kN∙m, р= 20 kN/m.
Решение. Нека разгледаме равновесието на рамката. Мислено освободете рамката от връзките на опорите (фиг. 40, b) и изберете обекта на равновесие. Рамката е натоварена с активен товар под формата на произволна равнинна система от сили. Вместо изхвърлени връзки, ние прилагаме реакции към равновесния обект: върху шарнирно фиксирана опора А- вертикален V Aи хоризонтално H A, и върху шарнирно подвижна опора IN- вертикална реакция V БОчакваната посока на реакциите е показана на фиг. 40, b.

Фиг.40.Проектна схема на рамката и равновесния обект за пример 18:
А– проектна схема; b– обект на равновесие
Създаваме следните условия на равновесие:
Σ Fx = 0; -H A + Е = 0; H A= 50 kN.
Σ м А = 0; V Б∙6 + М - р∙6∙3 - Е∙6 = 0; V Б= 100 kN.
Σ Fy = 0; V A + V Б - р∙6 = 0; V A= 20 kN.
Тук посоката на въртене около момента, който сочи обратно на часовниковата стрелка, обикновено се приема за положителна.
За да проверим правилността на изчислението на реакциите, използваме условието за равновесие, което ще включва всички опорни реакции, например:
Σ m C = 0; V Б∙3 + М – H A∙6 – V A∙3 = 0.
След заместване на числовите стойности получаваме тъждеството 0=0.
Така посоките и величините на опорните реакции се определят правилно.
Пример 19.Определете опорните реакции на рамката (фиг. 41, А).

Фиг.41
Решение.Както в предишния пример, рамката се състои от две части, свързани с ключова панта СЪС.Заменяме разпределеното натоварване, приложено към лявата страна на рамката, с полученото Q 1, а вдясно - резултатната Q 2 където Q 1 = Q 2 = 2kN.
1) Намерете реакцията Р Бот уравнението Σ М С (слънце) = 0; → Р Б= 1kN;