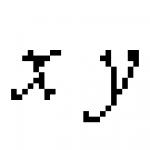За всяка логическа формула, използвайки трансформации на идентичност, могат да се конструират безкрайно много еквивалентни на нея формули. В алгебрата на логиката една от основните задачи е търсенето на канонични форми (т.е. формули, конструирани според едно правило, канонът).
Ако една логическа функция се изразява чрез дизюнкция, конюнкция и отрицание на променливи, тогава тази форма на представяне се нарича нормална.
Сред нормалните форми се разграничават перфектни нормални форми (тези форми, в които функциите са записани по уникален начин).
Перфектна дизюнктивна нормална форма (PDNF)
Определение. Формулата се нарича елементарна връзка, ако е образувана от връзката на определен брой променливи или техните отрицания.
Примери: y, ¬ y, x 1 ∧ ¬ x 2 ∧ x 3 ∧ x 4
Определение. Една формула се нарича дизюнктивна нормална форма (DNF), ако е дизюнкция на неповтарящи се елементарни връзки.
DNF се записва в следната форма: F 1 ∨ F 2 ∨ ... ∨ F n , където F i е елементарната конюнкция
Примери: ¬ x 1 ∧ x 2 ∨ x 1 ∧ ¬ x 2 ∨ x 1 ∧ ¬ x 2 ∧ x 3 , ¬ y 1 ∨ y 1 ∧ y 2 ∨ ¬ y 2
Определение. Логическа формула в k променливи се нарича перфектна дизюнктивна нормална форма (PDNF), ако:
1) формулата е DNF, в която всяка елементарна връзка е връзка от k променливи x 1, x 2, ..., x k, а на i-то място на тази връзка има или променлива x i, или нейното отрицание ;
2) всички елементарни конюнкции в такава ДНФ са по двойки различни.
Пример: (¬ x 1 ∧ x 2 ∧ x 3) ∨ (x 1 ∧ ¬ x 2 ∧ x 3) ∨ (x 1 ∧ x 2 ∧ ¬ x 3)
Перфектна конюнктивна нормална форма (PCNF)
Определение. Формула се нарича елементарна дизюнкция, ако е образувана от дизюнкция на определен брой променливи или техните отрицания.
Примери: ¬ x 3, x 1 ∨ x 2, x 1 ∨ x 2 ∨ ¬ x 3
Определение. Една формула се нарича конюнктивна нормална форма (CNF), ако е конюнкция на неповтарящи се елементарни дизюнкции.
CNF се записва в следната форма: F 1 ∧ F 2 ∧ ... ∧ F n , където F i е елементарна дизюнкция
Примери: (x 1 ∨ ¬ x 2) ∧ x 3, (x 1 ∨ x 2) ∧ (¬ x 1 ∨ x 2 ∨ x 3) ∧ (x 1 ∨ ¬ x 2 ∨ ¬ x 3)
Определение. Логическа формула в k променливи се нарича перфектна конюнктивна нормална форма (CPNF), ако:
1) формулата е CNF, в която всяка елементарна дизюнкция е дизюнкция на k променливи x 1, x 2, ..., x k, а на i-то място на тази дизюнкция има или променлива x i, или нейното отрицание;
2) всички елементарни дизюнкции в такава КНФ са по двойки различни.
Пример: (x 1 ∨ x 2 ∨ x 3) ∧ (¬ x 1 ∨ ¬ x 2 ∨ x 3)
забележи това всяка логическа функция, която не е идентично равна на 0 или 1, може да бъде представена като SDNF или SKNF.
Алгоритъм за конструиране на SDNF с помощта на таблица на истината
- Изберете всички редове на таблицата, в които стойността на функцията е равна на единица.
- За всеки такъв ред напишете връзката на всички променливи, както следва: ако стойността на някаква променлива в този набор е равна на 1, тогава включваме самата променлива в връзката, в противен случай нейното отрицание.
- Свързваме всички получени конюнкции с операции на дизюнкция.
Алгоритъм за конструиране на SCNF с помощта на таблица на истината
- Изберете всички редове на таблицата, в които стойността на функцията е нула.
- За всеки такъв ред напишете дизюнкцията на всички променливи, както следва: ако стойността на някаква променлива в този набор е равна на 0, тогава включваме самата променлива в конюнкцията, в противен случай нейното отрицание.
- Свързваме всички получени дизюнкции с конюнкционни операции.
Анализът на алгоритмите показва, че ако в повечето от редовете на таблицата на истината стойността на функцията е 0, тогава за получаване на нейната логическа формула е по-добре да се конструира SDNF, в противен случай - SCNF.
Пример: Дадена е таблица на истинност на логическа функция от три променливи. Изградете логическа формула, която изпълнява тази функция.
| х | г | z | F(x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
защото на повечето редове от таблицата на истината стойността на функцията е 1, тогава ще конструираме SCNF. В резултат на това получаваме следната логическа формула:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)
Нека проверим получената формула. За да направим това, ще изградим таблица на истинност за функцията.
| х | г | z | ¬ x | ¬ x ∨ y ∨ z | ¬ z | ¬ x ∨ y ∨ ¬ z | F(x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Сравнявайки оригиналната таблица на истината и тази, конструирана за логическата формула, отбелязваме, че колоните с функционални стойности съвпадат. Това означава, че логическата функция е конструирана правилно.
просто съчетание Наречен съчетание един или няколко променливи, при това всеки променлива отговаря Не Повече ▼ един пъти (или себе си, или нея отрицание).
Например, е проста връзка,
Дизюнктивна нормално форма(DNF) Наречен дизюнкция просто съюзи.
Например изразът е DNF.
перфектен дизюнктивен нормално форма(SDNF) Наречен като този дизюнктивен нормално форма, при който V всеки съчетание включени всичко променливи дадено списък (или себе си, или техен отказ), и V един И сила на звука един и същДобре.
Например изразът е DNF, но не и SDNF. Изразяване ![]() е SDNF.
е SDNF.
Подобни определения (със замяна на конюнкция с дизюнкция и обратно) са верни за CNF и SKNF. Нека дадем точната формулировка.
просто дизюнкция Наречен дизюнкция един или няколко променливи, при това всеки променлива включени Не Повече ▼ един пъти (или себе си, или нея отрицание).Например, изразът е проста дизюнкция,
Съединителен нормално форма(KNF) Наречен съчетание просто дизюнкции(например изразът е CNF).
Перфектната конюнктивна нормална форма (PCNF) е CNF, в която всяка проста дизюнкция включва всички променливи от даден списък (или самите тях, или техните отрицания) и в същия ред.
Например изразът ![]() е SKNF.
е SKNF.
Нека представим алгоритми за преход от една форма към друга. Естествено, в конкретни случаи (с определен творчески подход) използването на алгоритми може да бъде по-трудоемко от простите трансформации, използващи конкретен тип на дадена форма:
а) преход от DNF към CNF
Алгоритъмът за този преход е следният: поставяме две отрицания над DNF и, използвайки правилата на De Morgan (без да докосваме горното отрицание), намаляваме отрицанието на DNF обратно до DNF. В този случай трябва да отворите скобите, като използвате правилото за абсорбция (или правилото на Блейк). Отрицанието (горно) на получената DNF (отново според правилото на de Morgan) веднага ни дава CNF:
Обърнете внимание, че CNF може да се получи и от оригиналния израз, ако извадим приизвън скоби;
б) преход от CNF към DNF
Този преход се извършва чрез просто отваряне на скобите (отново се използва правилото за поглъщане)
Така получихме DNF.
Обратният преход (от SDNF към DNF) е свързан с проблема за минимизиране на DNF. Това ще бъде обсъдено по-подробно в раздела. 5, тук ще покажем как да опростим DNF (или SDNF) според правилото на Blake. Този тип DNF се нарича съкратено DNF;
в) съкращение DNF (или SDNF) от правило Блейк
Прилагането на това правило се състои от две части:
Ако сред дизюнктните членове в ДНФ има термини ![]() , тогава към цялата дизюнкция добавяме члена ДА СЕ 1 ДА СЕ 2. Извършваме тази операция няколко пъти (евентуално последователно или едновременно) за всички възможни двойки термини и след това прилагаме нормална абсорбция;
, тогава към цялата дизюнкция добавяме члена ДА СЕ 1 ДА СЕ 2. Извършваме тази операция няколко пъти (евентуално последователно или едновременно) за всички възможни двойки термини и след това прилагаме нормална абсорбция;
Ако добавеният термин вече се съдържа в DNF, тогава той може да бъде напълно отхвърлен, например,
или
Разбира се, съкратеното DNF не е еднозначно дефинирано, но всички съдържат еднакъв брой букви (например има DNF ![]() , след прилагане на правилото на Блейк към него, може да се стигне до DNF, еквивалентен на това):
, след прилагане на правилото на Блейк към него, може да се стигне до DNF, еквивалентен на това):
в) преход от DNF към SDNF
Ако в някаква проста връзка липсва променлива, например, z, вмъкнете израза в него и след това отворете скобите (ние не пишем повтарящи се несвързани термини). Например:
г) преход от КНФ към СКНФ
Този преход се извършва по начин, подобен на предишния: ако в проста дизюнкция липсва някаква променлива (например, z, след което добавяме израз към него (това не променя самата дизюнкция), след което отваряме скобите, използвайки закона за разпределение:
Така SKNF се получава от CNF.
Имайте предвид, че минималната или намалена CNF обикновено се получава от съответната DNF.
Нормални форми на логически функции Представянето на булева функция под формата на дизюнкция на конюнктивни членове на съставните части на единицата Ki 2.7 се нарича дизюнктивна нормална форма на DNF на тази функция. съдържа точно една от всички логически променливи, взети с или без отрицания, тогава тази форма на представяне на функция се нарича перфектна дизюнктивна нормална форма SDNF на тази функция. Както можете да видите, когато съставяте SDNF функция, трябва да създадете дизюнкция на всички минтерми, за които функцията приема стойност 1.
Споделете работата си в социалните мрежи
Ако тази работа не ви подхожда, в долната част на страницата има списък с подобни произведения. Можете също да използвате бутона за търсене
Лекция 1.xx
Нормални форми на логически функции
Представяне на булева функция под формата на дизюнкция на конюнктивни членове (единична съставна част) K i
, (2.7)
Наречен дизюнктивна нормална форма(DNF) на тази функция.
Ако всички съединителни членове в DNF саминтерс , т.е. съдържа точно една от всички логически променливи, взети със или без отрицания, тогава тази форма на представяне на функция се наричаперфектна дизюнктивна нормална форма(SDNF ) тази функция. Нарича се SDNFперфектен , защото всеки член в дизюнкцията включва всички променливи;дизюнктивен , защото основната операция във формулата е дизюнкция. Концепция “нормална форма” означава недвусмислен начин за записване на формула, която изпълнява дадена функция.
Като се има предвид горното, от Теорема 2.1 следва следната теорема.
Теорема 2. Всяка булева функция(не идентично 0) могат да бъдат представени в SDNF, .
Пример 3. Нека имаме таблица с дадена функция f (x 1 , x 2 , x 3 ) (Таблица 10).
Таблица 10
|
f (x 1, x 2, x 3) |
|||
Въз основа на формула (2.6) получаваме:
Както можете да видите, когато съставяте SDNF функция, трябва да създадете дизюнкция на всички минтерми, за които функцията приема стойност 1.
Представяне на булева функция под формата на конюнкция на дизюнктивни членове (нулева съставна част) D i
, (2.8)
Наречен конюнктивна нормална форма(CNF) на тази функция.
Ако всички дизюнктивни термини на CNF са maxterms , т.е. съдържа точно една от всички логически променливи на функцията, взети със или без отрицания, тогава такава CNF се наричасъвършен конюнктив нормална форма(SKNF) на тази функция.
Теорема 3. Всяка булева функция(не е идентичен на 1) могат да бъдат изпратени до SKNF, и такова представяне е единственото.
Доказателството на теоремата може да бъде извършено подобно на доказателството на теорема 2.1 въз основа на следната лема на Шанън за конюнктивно разлагане.
Лема на Шанън . Всяка булева функция f (x 1, x 2, …, x m) от m променливите могат да бъдат представени по този начин:
. (2.9)
Трябва да се отбележи, че и двете форми на представяне на логическа функция (DNF и CNF) са теоретично равни по своите възможности: всяка логическа формула може да бъде представена както в DNF (с изключение на идентичната нула), така и в CNF (с изключение на идентичната ). В зависимост от ситуацията, представянето на функция в една или друга форма може да бъде по-кратко.
В практиката най-често се използва DNF, тъй като тази форма е по-позната на човек: от детството той е по-свикнал да добавя продукти, отколкото да умножава суми (в последния случай той интуитивно има желание да отвори скобите и по този начин да премине към DNF).
Пример 4. За функцията f (x 1 , x 2 , x 3 ), дадено от таблицата. 10, напишете го на SKNF.
За разлика от SDNF, когато компилирате SCNF в таблицата на истината на логическа функция, трябва да разгледате комбинациите от променливи, при които функцията приема стойност 0, и да създадете връзка на съответните maxterms,но променливите трябва да се вземат с обратна инверсия:
Трябва да се отбележи, че е невъзможно директно преминаване от SDNF на функция към нейния SCNF или обратно. При опити за такива трансформации резултатите са функции, противоположни на желаните. Изразите за функциите SDNF и SCNF могат да бъдат директно получени само от неговата таблица на истината.
Пример 5. За функцията f (x 1 , x 2 , x 3 ), дадено от таблицата. 10, опитайте да превключите от SDNF към SKNF.
Използвайки резултата от пример 2.3, получаваме:
Както можете да видите, при общата инверсия получихме SCNF на логическа функция, която е обратна на функцията, получена в пример 2.4:
защото съдържа всички maxterms, които не са в израза за SCNF на разглежданата функция.
1. Използвайки свойствата на операциите (вижте таблица 9) идентичност (), сума по модул 2 (), импликация (), преминаваме към операциите И, ИЛИ, НЕ (в булевата база).
2. Използвайки свойствата на отрицанието и законите на Де Морган (вижте таблица 9), ние гарантираме, че операциите на отрицание се прилагат само към отделни променливи, а не към цели изрази.
3. Използвайки свойствата на логическите операции И и ИЛИ (виж Таблица 9), получаваме нормалната форма (DNF или CNF).
4. Ако е необходимо, преминете към перфектни форми (SDNF или SKNF). Например, за да получите SCNF, често трябва да използвате свойството: .
Пример 6. Преобразувайте логическа функция в SKNF
Извършвайки стъпките на горния алгоритъм в ред, получаваме:
Използвайки свойството на абсорбция, получаваме:
Така получихме функцията CNF f (x 1, x 2, x 3 ). За да получите неговия SCNF, трябва да повторите всяка дизюнкция, в която липсва някоя променлива, два пъти с тази променлива и с нейното отрицание:
2.2.6. Минимизиране на логическите функции
Тъй като същата логическа функция може да бъде представена каточ лични формули, след това намиране на най-простата формаР mule, дефинираща булева функция, опростява логическата схема, която имплементира булевата функцияда ция. Минимална форма lО логическа функцияв някаква основа можем да разгледаме такава, която съдържа минималния брой суперпозиции на забавлениеДа се ции на основата, позволяващи скоби. Въпреки това е трудно да се изгради ефективенл алгоритъм за такова минимизиране за получаване на минималната скоба r ние.
Нека разгледаме по-опростен проблем за минимизиране при синтеза на комбинационни схеми, в който търсим не минималната скобена форма на функция, а нейната минимална DNF. Има прости, ефективни алгоритми за тази задача.
Метод на Куайн
Функцията, която трябва да бъде минимизирана, е представена в SDNF и към нея се прилагат всички възможни непълни операции на залепване
, (2.10)
и след това абсорбция
, (2.11)
и тази двойка стъпки се прилага многократно. По този начин е възможно да се намали ранга на термините. Тази процедура се повтаря, докато не остане нито един термин, който може да бъде свързан с друг термин.
Имайте предвид, че лявата страна на уравнение (2.10) може незабавно да бъде минимизирана по по-прост и по-очевиден начин:
Този метод е лош, защото при такова директно минимизиране съединителните термини или изчезват, въпреки че все още има възможни случаи на тяхното използване за залепване и абсорбиране с останалите термини.
Трябва да се отбележи, че методът на Quine е доста трудоемък, така че вероятността от грешки по време на трансформациите е доста висока. Но предимството му е, че теоретично може да се използва за произволен брой аргументи и с увеличаването на броя на променливите трансформациите стават по-малко сложни.
Метод на картата на Карно
Методът на картите на Карно (таблици) е по-нагледен, по-малко трудоемък и надежден начин за минимизиране на логическите функции, но използването му е практически ограничено до функции на 3-4 променливи, максимум 5-6 променливи.
Карта на Карно това е двуизмерна таблична форма за представяне на таблицата на истината на булева функция, която ви позволява лесно да намерите минималните DNF на логически функции в графична визуална форма. Всяка клетка от таблицата е свързана с SDNF minterm на функцията, която се минимизира, и по такъв начин, че всички оси на симетрия на таблицата съответстват на зони, които са взаимно обратни по отношение на някаква променлива. Това подреждане на клетките в таблицата улеснява определянето на залепващите условия на SDNF (различаващи се в знака на инверсия само на една променлива): те са разположени симетрично в таблицата.
Таблици на истината и карти на Карно за функциите И и ИЛИ на две лентид Променливите са представени на фиг. 8. Във всяка клетка на картата се записва стойностА Стойността на функция в набора от стойности на аргументи, съответстващи на тази клеткаН другарю
А) И б) ИЛИ
Ориз. 8. Пример за карти на Карно за функции на две променливи
В картата на Karnaugh има само едно 1 за функцията And, така че не може да бъде залепено към нищо. Изразът за минималната функция ще съдържа само термина, съответстващ на това 1:
f = x y .
В картата на Карно за функцията ИЛИ вече има три 1 и можете да направите две залепващи двойки, като 1 съответства на термина xy , се използва два пъти. В израза за минималната функция трябва да запишете условията за двойките, които се слепват, като оставите в тях всички променливи, които не се променят за тази двойка, и премахнете променливите, които променят стойността си. За хоризонтално залепване получавамех , и за вертикалниг , като резултат получаваме израза
f = x + y.
На фиг. 9 показва таблиците на истината на две функции на три променливи (А ) и техните карти на Карно ( b и c). Функция f 2 се различава от първия по това, че не е дефиниран върху три набора от променливи (в таблицата това е обозначено с тире).
При определяне на минималната DNF функция се използват следните правила. Всички клетки, съдържащи 1, се комбинират в затворени правоъгълни области, наречени k-кубове, където k = log 2 K, K количество 1 в правоъгълна площ. В този случай всяка област трябва да бъде правоъгълник с брой клетки 2 k, където k = 0, 1, 2, 3, …. За k = Извиква се 1 правоъгълникединият е куб и съдържа 2 1 = 2 единици; за k = 2 правоъгълник съдържа 2 2 = 4 единици и се наричадвукуб; за k = 3 област от 2 3 = 8 единици се наричаттрикуб ; и т.н. Могат да се извикат единици, които не могат да бъдат комбинирани в правоъгълницинулеви кубчета , които съдържат само една единица (2 0 = 1). Както се вижда, за дорик зоните могат да имат квадратна форма (но не е задължително), а ако са нечетник само правоъгълници.
|
b c |
||||||
Ориз. 9. Пример за карти на Карно за функции на три променливи
Тези региони могат да се припокриват, тоест едни и същи клетки могат да влизат в различни региони. Тогава минималната DNF функция се записва като дизюнкция на всички конюнктивни членове, съответстващи на k - кубчета.
Всяка от посочените области на картата на Карно е представена в минимална DNF чрез конюнкция, броят на аргументите в която ек по-малко от общия брой аргументи на функциятам , т.е. това число е равномк . Всяка връзка на минимален DNF се състои само от онези аргументи, които за съответната област на картата имат стойности или без инверсии, или само с инверсии, т.е. не променят значението си.
По този начин, когато покривате клетки на картата със затворени области, трябва да се стремите да гарантирате, че броят на областите е минимален и всяка област съдържа възможно най-много клетки, тъй като в този случай броят на термините в минималната DNF ще бъде минимален и броят на аргументите в съответната връзка ще бъде минимален.
За функцията според картата на Карно на фиг. 9, b намираме
тъй като за горната затворена област променливите x 1 и x 2 имат стойности без инверсии, за по-нискитех 1 въпроси с инверсия их 3 без обръщане.
Недефинирани стойности в картата на фиг. 9, V може да се дефинира допълнително чрез замяната му с нула или единица. За тази функция е ясно, че е по-изгодно да замените и двете недефинирани стойности с 1. В този случай се формират две области, които са различни видове 2-кубчета. Тогава изразът за минималната DNF функция ще бъде както следва:
При изграждането на затворени зони е разрешено картата на Карно да се сгъва в цилиндър както хоризонтално, така и вертикално.Р тикални оси с обединение на противоположни лицаР единици, разположени по ръбовете на картата на симетрия на Карноч но могат и да се комбинират.
Картите на Карно могат да бъдат съставени по различни начини (фиг. 10).
|
х 2 х 3 |
||||||||||
а б
Ориз. 10. Различни начини за изобразяване на карти на Карно
за функция на 3 променливи
Но най-удобните опции за карти на Karnaugh за функции от 2-4 променливи са тези, показани на фиг. 11 таблици, защото показват за всяка клеткаА Имаме всички променливи в пряка или обратна форма.
а б
Ориз. единадесет. Най-удобното изображение на картите на Carnaugh
за функции 3 (а) и 4 (б) променливи
За функции от 5 и 6 променливи, методът, показан на фиг. 10, V .
Ориз. 12. Изображение на карта на Карно за функция от 5 променливи
Ориз. 13. Изображение на карта на Карно за функция от 6 променливи
Други подобни произведения, които може да ви заинтересуват.vshm> |
|||
| 9020. | ПРИНЦИПЪТ НА ДВОЙСТВЕНОСТТА. РАЗШИРЯВАНЕ НА БУЛЕВИ ФУНКЦИИ В ПРОМЕНЛИВИ. ПЕРФЕКТНИ РАЗДЕЛИТЕЛНИ И СЪЕДИНИТЕЛНИ НОРМАЛНИ ФОРМИ | 96,34 KB | |
| Тази теорема е конструктивна по своята същност, тъй като позволява на всяка функция да конструира формула, която я прилага под формата на перфектен d.n. f. За целта в таблицата на истината за всяка функция маркираме всички редове, в които | |||
| 6490. | Описание и минимизиране на логически функции | 187,21 KB | |
| Връзката между аргументите на функцията и нейните стойности се изразява в словесна форма. Пример: Функция с три аргумента приема стойност, когато всеки два или повече аргумента на функцията са равни. Състои се от конструиране на таблица на истината, съдържаща функционални стойности за всички набори от стойности на аргументи. В този пример, използвайки таблицата на истината, получаваме следния запис под формата на DNF... | |||
| 6707. | Проектиране на релационни бази данни. Проблеми на дизайна в класическия подход. Принципи на нормализация, нормални форми | 70,48 KB | |
| Какво е проект за релационна база данни Това е набор от взаимосвързани релации, в които са дефинирани всички атрибути, уточнени са първичните ключове на релациите и са посочени някои допълнителни свойства на релациите, които се отнасят до принципите за поддържане на целостта. Следователно дизайнът на базата данни трябва да бъде много точен и проверен. Всъщност проектът за база данни е основата на бъдещ софтуерен пакет, който ще се използва доста дълго време и от много потребители. | |||
| 4849. | Форми и методи за осъществяване на държавни функции | 197,3 KB | |
| Терминът „функция“ далеч не е същият смисъл в местната и чуждестранната научна литература. Във философски и общосоциологически план той се разглежда като „външно проявление на свойствата на даден обект в дадена система от отношения”; като набор от обикновени или специфични действия на лица или органи | |||
| 17873. | Формиране на логически UUD за ученици от 3 клас | 846,71 KB | |
| Психологически и педагогически аспекти на проблема с формирането на логически универсални действия при учениците от началното училище. Методи за оценка на формирането на логически UUD. Разработването на концепция за развитие на универсалната образователна дейност в системата на общото образование отговаря на нови обществени потребности. Най-важната задача на съвременната образователна система е формирането на универсални образователни дейности на UUD. Формирането на универсални образователни дейности е ключът към предотвратяването на училищните трудности. | |||
| 2638. | Техническа реализация на логически връзки в системи за автоматично блокиране | 1,04 MB | |
| Техническа реализация на логически връзки в системи за автоматично блокиране Техническа реализация на алгоритми за управление на триразрядни и четириразрядни батерии може да се постигне чрез релейни контактни и безконтактни дискретни и интегрални логически елементи... | |||
| 10203. | ПРИЛОЖЕНИЕ НА КОНЦЕПЦИЯТА ЗА РИСКОРИЕНТИРАН ПОДХОД ЗА ИЗГРАЖДАНЕ НА СТРУКТУРНИ И ЛОГИЧЕСКИ МОДЕЛИ НА ВЪЗНИКВАНЕ И РАЗВИТИЕ НА АВАРИЙНИ СИТУАЦИИ | 70,8 KB | |
| Общ анализ на риска Производствената среда се насища с мощни технологични системи и технологии, които правят човешкия труд продуктивен и по-малко физически труден, но по-опасен. Рискът се характеризира с неочакваност и внезапност на възникването на опасна ситуация. Всеки ден сме изправени пред многобройни рискове, но повечето от тях остават потенциални.Теорията на риска предвижда количествена оценка на отрицателното въздействие върху човек, както и щетите върху неговото здраве и живот. | |||
| 11576. | Понятие, видове и форми на сделките. Последици от неспазване на необходимата форма на сделките | 49,82 KB | |
| Признаване на сделката за недействителна Видове недействителни сделки. Приложната стойност на курсовата работа е в опростяването на концепцията за транзакция, тоест нейното публично представяне в по-достъпна форма. | |||
| 6213. | Функционална апроксимация | 3,08 MB | |
| Първият се състои в замяна на определена функция, определена аналитично или таблично, с друга функция, близка до оригиналната, но по-проста и удобна за изчисления. Например, заместването на функция с полином ви позволява да получите прости формули за числено интегриране и диференциране; Замяната на таблицата с апроксимираща функция ви позволява да получите стойности в нейните междинни точки. Възниква и вторият проблем: възстановяване на функция на определен сегмент от стойностите на функцията, дадени на този сегмент в дискретен набор от точки. Отговорът на този въпрос... | |||
| 14058. | Еволюция на държавните функции | 29,99 KB | |
| Руската държава като правен феномен трябва преди всичко да осигури изпълнението на предназначението на държавата, както и на нейните основни конституционни характеристики като демократична федерална правна социална светска държава с републиканска форма на управление. Основната цел на държавата се определя от чл. | |||
Определение 1.Съединителен моном (елементарна връзка)на променливи е връзката на тези променливи или техните отрицания.
Например, е елементарен съюз.
Определение 2.Дизюнктивен моном (елементарна дизюнкция)от променливи е дизюнкция на тези променливи или техните отрицания.
Например, е елементарна дизюнкция.
Определение 3.Формула, която е еквивалентна на дадена формула на пропозиционалната алгебра и е дизюнкция на елементарни конюнктивни мономи, се нарича дизюнктивна нормална форма(DNF) на тази формула.
Например,– ДНФ.
Определение 4.Формула, която е еквивалентна на дадена формула на пропозиционалната алгебра и е конюнкция на елементарни дизюнктивни мономи, се нарича конюнктивна нормална форма(CNF) на тази формула.
Например, – KNF.
За всяка формула на пропозиционалната алгебра може да се намери набор от дизюнктивни и конюнктивни нормални форми.
Алгоритъм за построяване на нормални форми
Използвайки еквивалентите на логическата алгебра, заменете всички основни операции във формулата: конюнкция, дизюнкция, отрицание:
Отървете се от двойните негативи.
Приложете, ако е необходимо, свойствата на формулите за разпределение и абсорбция към операциите на конюнкция и дизюнкция.
2.6. Перфектни дизюнктивни и перфектни конюнктивни нормални форми
Всяка булева функция може да има много представяния под формата на DNF и CNF. Специално място сред тези представяния заемат перфектната DNF (SDNF) и перфектната CNF (SCNF).
Определение 1. Перфектна дизюнктивна нормална форма(SDNF) е DNF, в която всеки конюнктивен моном съдържа всяка променлива от набора точно веднъж, или себе си, или своето отрицание.
Структурно, SDNF за всяка формула на пропозиционална алгебра, намалена до DNF, може да се дефинира, както следва:
Определение 2. Перфектна дизюнктивна нормална форма(SDNF) на формула на пропозиционална алгебра се нарича нейната DNF, която има следните свойства:
Определение 3. Перфектен конюнктив нормална форма(SCNF) е CNF, в която всеки дизюнктивен моном съдържа всяка променлива от набора точно веднъж и се появява или самият той, или неговото отрицание.
Структурно, SCNF за всяка формула на пропозиционалната алгебра, редуцирана до CNF, може да се дефинира както следва.
Определение 4. Перфектен конюнктив нормална форма(SCNF) на дадена формула на пропозиционална алгебра се нарича CNF, която отговаря на следните свойства.
Теорема 1.Всяка булева функция на променливи, която не е идентично невярна, може да бъде представена в SDNF и то по уникален начин.
Методи за намиране на SDNF
1-ви метод
2-ри метод
изберете редовете, където формулата приема стойност 1;
ние съставяме дизюнкция от конюнкции при условие, че ако променлива е включена в конюнкцията със стойност 1, тогава записваме тази променлива; ако със стойност 0, тогава нейното отрицание. Получаваме SDNF.
Теорема 2.Всяка булева функция на променливи, която не е идентично вярна, може да бъде представена в SCNF и то по уникален начин.
Методи за намиране на SCNF
1-ви метод– използване на еквивалентни трансформации:
2-ри метод– използване на таблици на истината:
изберете редовете, където формулата приема стойност 0;
ние съставяме конюнкция от дизюнкции при условие, че ако променлива е включена в дизюнкцията със стойност 0, тогава записваме тази променлива; ако със стойност 1, тогава нейното отрицание. Получаваме SKNF.
Пример 1.Конструирайте CNF функции.
Решение
Нека елиминираме свързващото "" като използваме законите за трансформация на променливи:
= /законите на де Морган и двойното отрицание/ =
/разпределителни закони/ =
Пример 2.Дайте формулата на DNF.
Решение
Нека изразим логически операции с помощта на и:
= /нека класифицираме отрицанието като променливи и намалим двойните отрицания/ =
= /закон за дистрибутивност/ .
Пример 3.Напишете формулата в DNF и SDNF.
Решение
Използвайки законите на логиката, свеждаме тази формула до форма, съдържаща само дизюнкции на елементарни връзки. Получената формула ще бъде желаната DNF:
За да конструираме SDNF, нека създадем таблица на истината за тази формула:
Маркираме онези редове от таблицата, в които формулата (последната колона) приема стойност 1. За всеки такъв ред записваме формула, която е вярна на набора от променливи на този ред:
ред 1: ;
ред 3: ;
ред 5: .
Дизюнкцията на тези три формули ще приеме стойност 1 само за наборите от променливи в редове 1, 3, 5 и следователно ще бъде желаната идеална дизюнктивна нормална форма (PDNF):
Пример 4.Донесете формулата на SKNF по два начина:
а) използване на еквивалентни трансформации;
б) използване на таблица на истината.
Решение:
Нека трансформираме втората елементарна дизюнкция:
Формулата изглежда така:
б) съставете таблица на истината за тази формула:
Маркираме онези редове от таблицата, в които формулата (последната колона) приема стойност 0. За всеки такъв ред записваме формула, която е вярна на набора от променливи на този ред:
ред 2: ;
ред 6: .
Конюнкцията на тези две формули ще приеме стойност 0 само за наборите от променливи в редове 2 и 6 и следователно ще бъде желаната перфектна конюнктивна нормална форма (PCNF):
Въпроси и задачи за самостоятелно решаване
1. Използвайки еквивалентни трансформации, намалете формулите до DNF:
2. Използвайки еквивалентни трансформации, пренесете формулите в CNF:
3. Използвайки втория закон за разпределение, преобразувайте DNF в CNF:
а) ![]() ;
;
4. Преобразувайте дадените DNF в SDNF:
5. Преобразувайте дадения CNF в SCNF:
6. За дадени логически формули конструирайте SDNF и SCNF по два начина: с помощта на еквивалентни трансформации и с помощта на таблица на истинност.
б) ![]() ;
;
Дизюнктивни и конюнктивни нормални форми на пропозиционалната алгебра.За всяка пропозиционална логическа функция може да се изгради таблица на истината. Обратната задача също винаги е разрешима. Нека въведем няколко определения.
Елементарни съюзи (съюзни)се наричат конюнкции на променливи или техните отрицания, в които всяка променлива се среща най-много
веднъж.
Дизюнктивна нормална форма(DNF) е формула, която има формата на дизюнкция на елементарни връзки.
Елементарни дизюнкции (дизюнкции)се наричат дизюнкции на променливи със или без отрицания.
Съединителна нормална форма(CNF) е формула, която има формата на конюнкция на елементарни дизюнкции.
За всяка функция на пропозиционалната алгебра може да се намери набор от дизюнктивни и конюнктивни нормални форми.
Алгоритъм за конструиране на DNF:
1. Отидете на булеви операции, като използвате еквивалентни формули за трансформация.
2. Отидете на формули с близки отрицания, т.е. на формула, в която отрицанията са разположени не по-високо от над променливите - приложете законите на Де Морган.
3. Отворете скобите - приложете законите на дистрибутивността.
4. Вземете повтарящи се термини един по един - законът за идемпотентността.
5. Приложете законите на поглъщането и полупоглъщането.
Пример 6.Намерете DNF формули: .
В булевата алгебра е вярно принцип на дуалността. Тя е следната.
Функцията се извиква двойственкъм функцията if . Тези. За да се намери функция, двойна на дадена, е необходимо да се конструира отрицанието на функцията от отрицанията на аргументите.
Пример 7.Намерете функцията, двойна на .
Сред елементарните функции на алгебрата на логиката 1 е двойствена на 0 и обратно, x е двойствена на x, двойствена на , двойствена и обратно.
Ако във формулата F 1, представяща функцията, заместваме всички съюзи
върху дизюнкция, дизюнкция върху конюнкция, 1 върху 0, 0 върху 1, тогава получаваме формулата F *, представляваща функцията *, двойствена на .
Конюнктивната нормална форма (CNF) е двойна концепция за DNF, така че може лесно да бъде конструирана съгласно следната схема:
Пример 8.Намерете формулата CNF: .
Използвайки резултата от Пример 6, имаме
Перфектни дизюнктивни и перфектни конюнктивни нормални форми.Във всеки тип нормални форми (дизюнктивни и конюнктивни) може да се разграничи клас перфектни форми SDNF и SCNF.
Перфектната елементарна връзка е логическият продукт на всички променливи със или без отрицание и всяка променлива се появява в продукта само веднъж.
Всеки DNF може да бъде намален до SDNF чрез разделяне на конюнкции, които не съдържат всички променливи, т.е. чрез добавяне за липсващата променлива x i се умножава с помощта на закона за разпределение
Пример 9.Намерете SDNF за DNF от Пример 6
Перфектна елементарна дизюнкцияе логическата сума на всички променливи с или без отрицания и всяка променлива е включена в сумата само веднъж.
Всеки CNF може да бъде редуциран до SCNF чрез добавяне на член на връзката, който не съдържа никаква променлива X i чрез връзката и прилагане на закона за разпределение
Пример 10.Доведете KNF до SKNF:
За да конструирате SCNF, можете да използвате диаграмата
Пример 11.Намерете SCNF за формулата от пример 6.
Всяка функция има SDNF и освен това е уникален. Всяка функция има SCNF и освен това е уникален.
защото SDNF и SKNF са уникално дефинирани чрез формули; те могат да бъдат конструирани с помощта на таблицата на истинността на формулата.
За да се конструира SDNF, е необходимо да се изберат редовете, в които F приема стойност 1 и да се запишат перфектни елементарни конюнкции за тях. Ако стойността на променлива в желания ред на таблицата на истината е равна на единица, тогава в перфектна връзка тя се приема без отрицание, ако е нула, тогава с отрицание. След това перфектните конюнкции (броят им е равен на броя на единиците в таблицата) се свързват със знаци за дизюнкция.
За да се изгради SCNF с помощта на таблица на истината, е необходимо да се изберат редовете в нея, където F = 0, и да се запишат идеални елементарни дизюнкции, след което да се свържат със знаци за връзка. Ако в необходимия ред на таблицата на истината (F=0) стойността на променливата съответства на нула, тогава в перфектната клауза тя се взема без отрицание, ако е единица, тогава с отрицание.
Пример 12.Намерете SDNF и SCNF, като използвате таблицата на истината за формулата от пример 6.
Таблица 14 показва само крайната стойност F=10101101. Трябва сами да проверите валидността на това твърдение, като съставите подробна таблица на истината.
Таблица 14
| х | г | z | ||