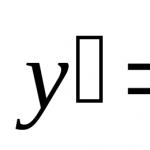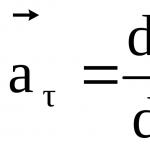Нека функциите имат производни на границата (n-1).
Помислете за детерминанта:  (1)
(1)
W(x) се нарича детерминанта на Wronski за функции.
Теорема 1.Ако функциите са линейно зависими в интервала (a, b), тогава техният Wronskian W(x) е идентично равен на нула в този интервал.
Доказателство.Съгласно условията на теоремата връзката е изпълнена
, (2) където не всички са равни на нула. Позволявам . Тогава
![]() (3). Разграничаваме тази идентичност n-1 пъти и,
(3). Разграничаваме тази идентичност n-1 пъти и,
Замествайки вместо това получените им стойности в детерминанта на Wronsky,
получаваме:
 (4).
(4).
В детерминантата на Wronski последната колона е линейна комбинация от предходните n-1 колони и следователно е равна на нула във всички точки от интервала (a, b).
Теорема 2.Ако функциите y1,…, yn са линейно независими решения на уравнението L[y] = 0, чиито всички коефициенти са непрекъснати в интервала (a, b), тогава Wronskian на тези решения е различен от нула във всяка точка от интервал (a, b).
Доказателство.Да приемем обратното. Има X0, където W(X0)=0. Нека създадем система от n уравнения
 (5).
(5).
Очевидно системата (5) има ненулево решение. Нека (6).
Нека направим линейна комбинация от решения y1,…, yn.
Y(x) е решение на уравнението L[y] = 0. В допълнение, . По силата на теоремата за уникалността решението на уравнението L[y] = 0 с нулеви начални условия може да бъде само нула, т.е.
Получаваме идентичността, при която не всички са равни на нула, което означава, че y1,..., yn са линейно зависими, което противоречи на условията на теоремата. Следователно, няма такава точка, където W(X0)=0.
Въз основа на теорема 1 и теорема 2 може да се формулира следното твърдение. За да бъдат n решения на уравнението L[y] = 0 линейно независими в интервала (a, b), е необходимо и достатъчно техният Wronskian да не изчезва в нито една точка от този интервал.
Следните очевидни свойства на Wronskian също следват от доказаните теореми.
- Ако Вронскианът на n решения на уравнението L[y] = 0 е равен на нула в една точка x = x0 от интервала (a, b), в който всички коефициенти pi(x) са непрекъснати, тогава той е равен на нула във всички точки от този интервал.
- Ако Вронскианът на n решения на уравнението L[y] = 0 е различен от нула в една точка x = x0 от интервала (a, b), тогава той е различен от нула във всички точки от този интервал.
Така за линейността на n независими решения на уравнението L[y] = 0 в интервала (a, b), в който коефициентите на уравнението рi(x) са непрекъснати, е необходимо и достатъчно техният Wronskian да бъде ненулева поне в една точка от този интервал.
Деф.Система от елементи x 1,…,x m линейна. пр-ва V се нарича линейно зависима, ако ∃ λ 1 ,…, λ m ∈ ℝ (|λ 1 |+…+| λ m | ≠ 0), така че λ 1 x 1 +…+ λ m x m = θ .
Деф.Система от елементи x 1 ,…,x m ∈ V се нарича линейно независима, ако равенството λ 1 x 1 +…+ λ m x m = θ ⟹λ 1 =…= λ m =0.
Деф.Елемент x ∈ V се нарича линейна комбинация от елементи x 1 ,…,x m ∈ V, ако ∃ λ 1 ,…, λ m ∈ ℝ, така че x= λ 1 x 1 +…+ λ m x m.
Теорема (критерий за линейна зависимост):Система от вектори x 1 ,…,x m ∈ V е линейно зависима тогава и само ако поне един вектор от системата е линейно изразен през останалите.
Док. Необходимост:Нека x 1 ,…,x m е линейно зависим ⟹ ∃ λ 1 ,…, λ m ∈ ℝ (|λ 1 |+…+| λ m | ≠ 0), така че λ 1 x 1 +…+ λ m -1 x m -1 + λ m x m = θ. Тогава да кажем, че λ m ≠ 0
x m = (- ) x 1 +…+ (- ) x m -1.
Адекватност: Нека поне един от векторите е линейно изразен чрез останалите вектори: x m = λ 1 x 1 +…+ λ m -1 x m -1 (λ 1 ,…, λ m -1 ∈ ℝ) λ 1 x 1 + …+ λ m -1 x m -1 +(-1) x m =0 λ m =(-1) ≠ 0 ⟹ x 1 ,…,x m - линейно независими.
Преп. условие на линейна зависимост:
Ако една система съдържа нулев елемент или линейно зависима подсистема, тогава тя е линейно зависима.
λ 1 x 1 +…+ λ m x m = 0 – линейно зависима система
1) Нека x 1 = θ, тогава това равенство е валидно за λ 1 =1 и λ 1 =…= λ m =0.
2) Нека λ 1 x 1 +…+ λ m x m =0 – линейно зависима подсистема ⟹|λ 1 |+…+| λm | ≠ 0 . Тогава за λ 1 =0 също получаваме |λ 1 |+…+| λm | ≠ 0 ⟹ λ 1 x 1 +…+ λ m x m =0 – линейно зависима система.
Основа на линейното пространство. Координати на вектора в даден базис. Координати на сумите от вектори и произведението на вектор и число. Необходимо и достатъчно условие за линейна зависимост на система от вектори.
определение: Подредена система от елементи e 1, ..., e n на линейно пространство V се нарича база на това пространство, ако:
A) e 1 ... e n са линейно независими
B) ∀ x ∈ α 1 … α n, така че x= α 1 e 1 +…+ α n e n
x= α 1 e 1 +…+ α n e n – разгъване на елемента x в базиса e 1, …, e n
α 1 … α n ∈ ℝ – координати на елемент x в базиса e 1, …, e n
Теорема: Ако в линейно пространство V е даден базис e 1, …, e n, тогава ∀ x ∈ V колоната с координати x в базиса e 1, …, e n е еднозначно определен (координатите са еднозначно определени)
Доказателство:Нека x=α 1 e 1 +…+ α n e n и x=β 1 e 1 +…+β n e n
x= ⇔ = Θ, т.е. e 1, …, e n са линейно независими, тогава - =0 ∀ i=1, …, n ⇔ = ∀ i=1, …, n и т.н.
Теорема: нека e 1, …, e n е основата на линейното пространство V; x, y са произволни елементи от пространството V, λ ∈ ℝ е произволно число. Когато x и y се добавят, техните координати се добавят; когато x се умножава по λ, координатите x също се умножават по λ.
Доказателство: x= (e 1, …, e n) и y= (e 1, …, e n)
x+y= + = (e 1, …, e n)
λx= λ ) = (e 1, …, e n)
Лема 1: (необходимо и достатъчно условие за линейна зависимост на система от вектори)
Нека e 1 … е n е основата на пространството V. Система от елементи f 1 , …, f k ∈ V е линейно зависима тогава и само ако координатните колони на тези елементи в основата e 1, …, e n са линейно зависими
Доказателство:нека разширим f 1, …, f k според основата e 1, …, e n
f m = (e 1, …, e n) m = 1, …, k
λ 1 f 1 +…+λ k f k =(e 1, …, e n)[ λ 1 +…+ λ n ] т.е. λ 1 f 1 +…+λ k f k = Θ ⇔
⇔ λ 1 +…+ λ n = което трябваше да бъде доказано.
13. Размерност на линейното пространство. Теорема за връзката между размерност и базис.
определение:
Линейно пространство V се нарича n-мерно пространство, ако има n линейно независими елемента във V и система от всякакви n+1 елемента на пространството V е линейно зависима. В този случай n се нарича размерност на линейното пространство V и се означава с dimV=n.
Линейно пространство се нарича безкрайномерно, ако ∀N ∈ ℕ в пространството V съществува линейно независима система, съдържаща N елемента.
Теорема: 1) Ако V е n-мерно линейно пространство, тогава всяка подредена система от n линейно независими елемента от това пространство образува основа. 2) Ако в линейно пространство V има база, състояща се от n елемента, тогава размерността на V е равна на n (dimV=n).
Доказателство: 1) Нека dimV=n ⇒ в V ∃ n линейно независими елементи e 1, …, e n. Ще докажем, че тези елементи образуват основа, тоест ще докажем, че ∀ x ∈ V може да се разложи в e 1, …, e n . Нека добавим x към тях: e 1, ..., e n, x - тази система съдържа n+1 вектора, което означава, че е линейно зависима. Тъй като e 1, …, e n е линейно независим, тогава по Теорема 2 хлинейно изразено чрез e 1, …, e n, т.е. ∃ ,…, така че x= α 1 e 1 +…+ α n e n . Така че e 1, …, e n е основата на пространството V. 2) Нека e 1, …, e n е основата на V, така че има ∃ n линейно независими елемента във V. Нека вземем произволни f 1 ,…,f n ,f n +1 ∈ V – n+1 елемента. Нека покажем тяхната линейна зависимост. Нека ги разделим според основата им:
f m =(e 1, …,e n) = където m = 1,…,n Нека създадем матрица от координатни колони: A= Матрицата съдържа n реда ⇒ RgA≤n. Брой колони n+1 > n ≥ RgA ⇒ Колоните на матрица A (т.е. колони с координати f 1 ,…,f n ,f n +1) са линейно зависими. От лема 1 ⇒ ,…,f n ,f n +1 са линейно зависими ⇒ dimV=n.
Последица:Ако някоя база съдържа n елемента, тогава всяка друга база в това пространство съдържа n елемента.
Теорема 2: Ако системата от вектори x 1 ,… ,x m -1 , x m е линейно зависима и нейната подсистема x 1 ,… ,x m -1 е линейно независима, тогава x m се изразява линейно чрез x 1 ,… ,x m -1
Доказателство: защото x 1 ,… ,x m -1 , x m е линейно зависим, тогава ∃ , …, , ,
, …, | , | такова, че . Ако , , …, | => x 1 ,… ,x m -1 – са линейно независими, което не може да бъде. Това означава m = (-) x 1 +…+ (-) x m -1.
Линейни (векторни) пространства.
определение:Няколко ЛНаречен линейно (векторно) пространство , ако върху него са въведени две операции:
1) допълнение: за произволен x, y Є Lсума ( x + y) Є L,
2) умножение с число: за всяко x Є Lи произволно число λ произведението
λх Є L,
които отговарят на 8 аксиоми:
1) x + y = y + x, Където x,y Є L;
2) (x + y)+z = x+(y + z), Където x,y,z Є L;
3) има нулев елемент Ө такъв, че Ө + x = x, Където х Є L;
4) за всеки x Є Lима само един противоположен елемент
(-Х)такова, че x + (-x)= Ө;
5) 1 x = x, Където х Є L;
6) α(βх) = (αβ)х, Където x Є L, α и β-числа;
7) α(x + y) = αx + αy, Където x,y Є L, α-число;
8) (α + β) x = αx + βx, Където x Є L, α и β-числа.
Коментирайте: Елементите на линейното (векторно) пространство се наричат вектори .
Примери:
Множеството от реални числа е линейно пространство.
Наборите от всички вектори в равнината и в пространството са линейно пространство.
Наборът от всички матрици с еднакъв размер е линейно пространство.
Дадена е система от вектори в линейно пространство a 1, a 2, a 3, ... a n Є L.
определение:вектор α 1 a 1 + α 2 a 2 +…+ α n a n Є L, Където αi(i = 1,…,n) - числа, извикани линейна комбинация (LC) вектори a 1, a 2, a 3, ... a n.
определение:Линейна пространствена векторна система a 1, a 2, a 3, ... a n Є LНаречен линейно независим (LNI) , ако е линейна комбинация
α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n a n =0ако и само ако коефициентите
α 1 =α 2 =α 3 =…=α n =0.
определение:Векторна система a 1, a 2, a 3, ... a n Є LНаречен линейно зависими (LD) , ако има набор от числа α 1, α 2 , α 3 … α n, не всички от които са равни на 0, така че линейната комбинация α 1 a 1 + α 2 a 2 +…+ α n a n = 0.
Примери:
Двата вектора се наричат колинеарен, ако са успоредни на една права или лежат на една права.
1) Да разгледаме два ненулеви, неколинеарни вектора в равнината. Диагонал =0.
| а 2 |
Линейна комбинация е равна на нула, има ненулев коефициент, следователно два колинеарни вектора в равнината са линейно зависими.
Теорема 1. Необходимо и достатъчно условие за линейна зависимост.
За да бъде една система от вектори в линейно пространство линейно зависима, е необходимо и достатъчно някой вектор от тази система да бъде линейна комбинация от всички останали.
документ: Необходимост ().
Като се има предвид системата LZ. Необходимо е да се докаже, че един вектор е LC на всички останали.
a 1, a 2, a 3, ... a n– LZ система от вектори, т.е. сред α 1, α 2, α 3 … α n има ненулево число, такова че LC α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n a n = 0.
За да определим това, нека приемем, че коефициентът α 1 ≠ 0. Нека разделим двете страни на последното равенство на α 1 ≠ 0:
Следва, че а 1- LC на останалите вектори.
Необходимостта е доказана.
Адекватност ().
Нека един вектор е линейна комбинация от останалите. Необходимо е да се докаже, че системата от вектори е LZ.
Позволявам α n = α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n -1 a n -1.
α 1 a 1 + α 2 a 2 + α 3 a 3 +…+ α n -1 a n -1 - 1α n = 0.
Тъй като има ненулев коефициент, системата от вектори a 1, a 2, a 3, ... a n- линейно зависими.
Теорема 2.Система, съдържаща нулев вектор, е линейно зависима.
документ:Да разгледаме система от вектори, съдържаща нулев вектор. a 1, a 2, a 3, … a n ,Ө, Където Ө - нулев вектор. Очевидно е в сила следното равенство 0 a 1 + 0 a 2 +0 a 3 +…+ 5 Ө = 0.
Има ненулев коефициент равен на 5, а линейна комбинация е равна на 0, от което следва, че системата от вектори е LZ.
Теорема 3.Система, съдържаща линейно зависима подсистема, също ще бъде линейно зависима.
документ:Разгледайте системата от вектори a 1, a 2, ..., a k, a k+1 ... a n, Където a 1, a 2,..., a k- линейно зависимо парче. α 1 a 1 + α 2 a 2 + … +α k a k = 0. Има коефициент, различен от нула.
Очевидно при същите тези коефициенти равенството ще бъде спазено
α 1 a 1 + α 2 a 2 +…+α k a k +…+0· a k+1 +…+ 0·α n = 0.
От това следва, че системата от вектори е LZ.
Векторно пространство. Примери и най-прости свойства на векторни пространства.Линейна зависимост и независимост на система от вектори.Базис и ранг на крайна система от вектори.
Линейно или векторно пространство L(P) над поле P е непразно множество L, върху което се въвеждат следните операции:
1. добавяне, т.е. всяка двойка елементи от набор е свързана с елемент от същото множество, означено с x + yϵL
2. умножение по скалар (т.е. елемент от полето P), тоест всеки елемент λ ϵ P и всеки елемент x ϵ L е свързан с един елемент от L(P), означен като λx ϵ L(P ).
В този случай на операциите се налагат следните условия:
1. х+ г= y+ x, за всяко x,y ϵ L. (комутативност на свиването)
2.х+ (y+ z) = (x+ y) + z, x,y,z ϵ L. (асоциативност на свиването)
3.има такова нещо θ ϵ L, което х+ θ =x За anyx ϵ L (съществуване на неутрален елемент по отношение на добавянето), по-специално, не е празно;
4.за всяко x ϵ L има елемент -x ϵ L такъв, че х+(-x)= θ (наличие на противоположен елемент спрямо събирането).
5.(αβ)х=α(βх), (асоциативност на умножението със скалар)
6.1*x=x (унитарност: умножение с неутрален (чрез умножение) елемент на полето P запазва вектора).
7.(α+ β)* x= α* x+ β*x, (разпределимост на умножението с вектор спрямо събирането на скалари);
8. α * (x+y) = α *x+ α *y, (разпределимост на умножението по скалар спрямо събиране на вектори).
Елементите на множеството L се наричат вектори, а елементите на полето P - скалари. Свойства 1-4 съвпадат с аксиомите на абелевата група.
Най-простите светци:
1. Векторното пространство е абелева група при добавяне.
2. За всеки x ϵ L противоположният елемент -x ϵ L е уникален
3. 0*х=θ, за всеки x ϵ L
4. 1*(-x)=-x за всеки x ϵ L
5.α * θ = θ ,за всяко αϵ L
Пример за VPса m\in матрици с реални компоненти от същия ред с естествена дефиниция на операциите събиране и умножение. Матрици за броя на веществата
Линейна зависимост\(не) система от вектори (дефиниция, свойства)
Теорема. (Необходимо и достатъчно условие за линейна зависимост на система от вектори.)
Система от вектори във векторно пространство е линейно зависима тогава и само ако един от векторите на системата е линейно изразен чрез други вектори на тази система.
Доказателство. Необходимост. Нека системата e 1 ..e n е линейно зависима. Тогава, по дефиниция, той представя нулевия вектор нетривиално, т.е. има нетривиална линейна комбинация от тази система от вектори, равна на нулевия вектор:
α 1 e 1 +..+ α n e n =0, където поне един от коефициентите на тази линейна комбинация не е равен на нула. Нека α k ≠0 ,kϵ 1.2…n Разделете двете страни на предишното равенство на този ненулев коефициент (т.е. умножете по α k -1 *(α 1 e 1 +..+ αa n e n) =0
Нека означим: α k -1 α m =β m където mϵ 1,2…,k-1,k+1,..,n Тогава β 1 e 1+ … +β 1 e n =0, т.е. един от векторите на системата се изразява линейно чрез други вектори на тази система и т.н.
Адекватност. Нека един от векторите на системата бъде линейно изразен чрез други вектори на тази система: e k =γ 1 e 1+..+ γ n e n , Нека преместим вектора e k в дясната страна на това равенство: 0=γ 1 e 1+..+ γ n e n
Тъй като коефициентът на вектора e k е равен на -1≠0, тогава имаме нетривиално представяне на нула чрез система от вектори e 1 ..e n, което означава, че тази система от вектори е линейно зависима и т.н.
Теоремата е доказана.
Последица.
1. Система от вектори във векторно пространство е линейно независима тогава и само ако нито един от векторите на системата не е линейно изразен чрез други вектори на тази система.
2. Система от вектори, съдържаща нулев вектор или два равни вектора, е линейно зависима.
Последица.
Система, състояща се от един вектор, е линейно независима тогава и само ако този вектор е различен от нула.
Базисът е набор от вектори във векторно пространство, така че всеки вектор в това пространство може да бъде уникално представен като линейна комбинация от вектори от този набор - базисни вектори.
Броят на векторите, включени във всяка максимална линейно независима подсистема на дадена система от вектори, се нарича рангсистеми.
Теорема.Нека са дадени две системи П-размерни вектори:
а 1 ,а 2 ¼, а r (9)
b 1 ,b 2 ¼, bс, (10)
не непременно линейно независими и рангът на системата (9) е равен на числото к, системен ранг (10) – брой л. Ако първата система е линейно изразена през втората, тогава k £ l. Ако тези системите са еквивалентни, Че k = l.
Броят на елементите (кардиналност) на максимално линейно независимо подмножество на пространство не зависи от избора на това подмножество и се нарича ранг или измерение на пространството, а самото това подмножество се нарича основа
По-долу са дадени няколко критерия за линейна зависимост и, съответно, линейна независимост на векторните системи.
Теорема. (Необходимо и достатъчно условие за линейна зависимост на векторите.)
Една система от вектори е зависима тогава и само тогава, когато един от векторите на системата е линейно изразен чрез останалите на тази система.
Доказателство. Необходимост. Нека системата е линейно зависима. Тогава, по дефиниция, той представя нулевия вектор нетривиално, т.е. има нетривиална комбинация от тази система от вектори, равна на нулевия вектор:
където поне един от коефициентите на тази линейна комбинация не е равен на нула. Позволявам , .
Нека разделим двете страни на предишното равенство на този ненулев коефициент (т.е. умножете по:
Нека означим: , където .
тези. един от векторите на системата се изразява линейно през останалите на тази система и т.н.
Адекватност. Нека един от векторите на системата е линейно изразен чрез други вектори на тази система:
Нека преместим вектора вдясно от това равенство:
Тъй като коефициентът на вектора е равен на , тогава имаме нетривиално представяне на нула чрез система от вектори, което означава, че тази система от вектори е линейно зависима и т.н.
Теоремата е доказана.
Последица.
1. Система от вектори във векторно пространство е линейно независима тогава и само ако нито един от векторите на системата не е линейно изразен чрез други вектори на тази система.
2. Система от вектори, съдържаща нулев вектор или два равни вектора, е линейно зависима.
Доказателство.
1) Необходимост. Нека системата е линейно независима. Нека приемем обратното и има вектор на системата, който е линейно изразен чрез други вектори на тази система. Тогава според теоремата системата е линейно зависима и стигаме до противоречие.
Адекватност. Нека никой от векторите на системата не е изразен чрез останалите. Да приемем обратното. Нека системата е линейно зависима, но тогава от теоремата следва, че има вектор на системата, който се изразява линейно чрез други вектори на тази система и отново стигаме до противоречие.
2a) Нека системата съдържа нулев вектор. Да приемем със сигурност, че векторът :. Тогава равенството е очевидно
тези. един от векторите на системата се изразява линейно чрез другите вектори на тази система. От теоремата следва, че такава система от вектори е линейно зависима и т.н.
Имайте предвид, че този факт може да бъде доказан директно от линейно зависима система от вектори.
Тъй като , следното равенство е очевидно
Това е нетривиално представяне на нулевия вектор, което означава, че системата е линейно зависима.
2b) Нека системата има два равни вектора. Нека за. Тогава равенството е очевидно
Тези. първият вектор се изразява линейно чрез останалите вектори на същата система. От теоремата следва, че тази система е линейно зависима и т.н.
Подобно на предишното, това твърдение може да се докаже директно чрез дефиницията на линейно зависима система.Тогава тази система представя нулевия вектор нетривиално
откъдето следва линейната зависимост на системата.
Теоремата е доказана.
Последица. Система, състояща се от един вектор, е линейно независима тогава и само ако този вектор е различен от нула.