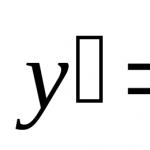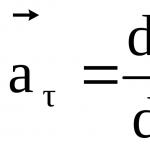Билет №1
противопроизводна функцияТеоремаДоказателство неопределен интеграл
Точката (X 0 ; Y 0) се нарича максимална точка
Доказателство:
Билет №2
ДоказателствоГеометрично значение
частно увеличение частична производна Геометрично значение
Билет №3
19. Определяне на точките на максимум и минимум на функцията z=f(x,y).Точката (X 0 ; Y 0) се нарича максимална точкафункция z=f(x;y), ако има δ-околност на точката (X 0 ;Y 0), така че неравенството f(x;y) е в сила
Билет №4 Чрез определен интеграл Имоти Доказателство.
Билет № 5
1. Антипроизводна функция. Теорема за разликата между две първоизводни (с доказателство). Неопределен интеграл: определение Функцията F(x) се извиква противопроизводна функция f(x) на интервала (a;b), ако за всяко x∈(a;b) е изпълнено равенството F"(x)=f(x). Теорема. Ако функцията F(x) е антипроизводна на функцията f(x) върху (a;b), тогава множеството от всички първоизводни за f(x) е дадено от формулата F(x)+C, където C= конст. Доказателство. Функцията F(x)+C е първоизводна на f(x). Наистина, (F(x)+C)"=F"(x)=f(x). Нека Ф(x) е друга първообразна функция f(x), различна от F(x), т.е. Ф"(x)=f(x). Тогава за всяко x∈(a;b) имаме (Ф(х)-F(x))"=Ф"(x)-F"(x)=f( x)-f(x)=0. А това означава, че Ф(х)-F(х)=C, C=const. Следователно Ф(x)=F(x)+C.Множеството от всички първообразни функции F(x)+C за f(x) се нарича неопределен интегрална функцията f(x) и се означава със символа ∫f(x)dx.
19. Определяне на точките на максимум и минимум на функцията z=f(x,y).Точката (X 0 ; Y 0) се нарича максимална точкафункция z=f(x;y), ако има δ-околност на точката (X 0 ;Y 0), така че неравенството f(x;y) е в сила
Билет №6
3. Изчисляване на определен интеграл по отсечка. Формула на Нютон-Лайбниц (извеждане).Ако функцията y=f(x) е непрекъсната на интервал и F(x) е някоя от нейните първоизводни върху (F"(x)=f(x)), тогава формулата ∫(от a до b) f( x) има )dx=F(b)-F(a). Тази формула е формулата на Нютон-Лайбниц. Помислете за идентичността: F(b)-F(a)=F(x n)-F(x 0)= (F(x n) -F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1) )-F(x 0)). Нека трансформираме всяка разлика в скоби, използвайки формулата на Лагранж: f(b)-f(a)=f'(c)*(b-a). Получаваме F(b)-F(a )=F'(c n)( x n -x n -1)+F'(c n -1)(x n -1 -x n -2)+F'(c 2)(x 2 -x 1)+F'(c 1)(x 1 -x 0 )= ΣF'(Ci)ΔXi=Σf(Ci)ΔXi, тоест F(b)-F(a)= Σf(Ci)ΔXi, където Ci е някаква точка от интервала (X i -1 ,X i). Тъй като функцията y=f(x) е непрекъсната върху , тогава тя е интегрируема върху . Следователно има граница на интегралната сума, равна на определения интеграл на f(x) Преминавайки към границата при λ=maxΔXi→0, получаваме F(b)-F( a)=lim Σf(Ci)ΔXi, тоест ∫(от a до b) f(x)dx=F( b)-F(a).
Извиква се функцията z=f(x;y). диференцируеми
11. Свойство на диференцируема функция: връзка между диференцируемостта на функцията z=f(x;y) и непрекъснатостта на функцията z=f(x;y) в точка (формулировка, доказателство). Ако функцията z=f(x;y) е диференцируема в точка M(x;y), тогава тя е непрекъсната в тази точка и има частни производни в нея. Доказателство. Нека функцията y=f(x) е диференцируема в точката x 0 . В този момент даваме на аргумента увеличение Δх. Функцията ще получи увеличение Δу. Нека намерим limΔx→0(Δy). limΔx→0(Δy)= limΔx→0((Δy*Δx)/Δx))= limΔx→0(Δy/Δx)* limΔx→0(Δx)=f"(x0)*0=0. Следователно, y =f(x) е непрекъсната в точката x 0.
Билет №7
19. Определяне на точките на максимум и минимум на функцията z=f(x,y).Точката (X 0 ; Y 0) се нарича максимална точкафункция z=f(x;y), ако има δ-околност на точката (X 0 ;Y 0), така че неравенството f(x;y) е в сила
Необходим знак за екстремум.
Ако непрекъсната функция z=z(x,y) има екстремум в точката P0(x0,y0), тогава всички нейни частични производни от първи ред в тази точка са или равни на нула, или не съществуват
Доказателство:Частната производна на функцията z=f(x,y) по отношение на x в точката P0(x0,y0) е производната на функцията на една променлива φ(x)=f(x,y0) в точката х-х0. Но в този момент функцията φ(x) очевидно има екстремум. Следователно, φ'(x0)=0. Тъй като φ'(x0)=f'x(x0,y0), тогава f'x(x0,y0)=0 По подобен начин може да се покаже, че f'y(x0, y0 )=0 . Теоремата е доказана.
Билет №8
6. Теорема за средната стойност (формулировка, доказателство, геометричен смисъл).Ако функцията f(x) е непрекъсната на отсечката , тогава има точка C∈ такава, че ∫(от a до b) f(x)dx=f(c)*(b-a). Доказателство. Съгласно формулата на Нютон-Лайбниц имаме ∫(от a до b) f(x)dx=F(x)|(от a до b)=F(b)-F(a), където F"(x )=f( x). Прилагайки теоремата на Лагранж (теоремата за крайното нарастване на функция) към разликата F(b)-F(a), получаваме F(b)-F(a)=F"(c )*(b-a)=f(c) *(b-a). Геометрично значение. Теоремата за f(x)≥0 има просто геометрично значение: стойността на определения интеграл е равна за някои C∈ (a;b) на площта на правоъгълник с височина f(c) и основа б-а. Числото f(c)=1/(b-a)∫(от a до b) f(x)dx се нарича средна стойност на функцията f(x) върху сегмента.
8. Частични нараствания на функцията z=f(x;y). Частични производни: определение и тяхното геометрично значение.Нека е дадена функцията z=f(x;y). Тъй като x и y са независими променливи, едната от тях може да се променя, докато другата остава постоянна. Нека дадем на променливата x увеличение ∆x, като запазим стойността на променливата y непроменена. Тогава функцията z ще получи увеличение, което ще извикаме частно увеличение z в x и означете ∆ x z. И така, ∆ x z=f(x+∆x;y)–f(x;y). По подобен начин получаваме частичното увеличение на z по отношение на y: ∆ y z=f(x;у+∆y)–f(x;y). Ако има ограничение lim∆x→0(∆ x z/∆x )=lim∆x→0( (f(x+∆x;y)-f(x;y))/∆x), тогава се нарича частична производнафункция z=f(x;y) в точката M(x;y) в променливата x и се означава с един от символите: z" x, δz/δx; f" x, δf/δx. Геометрично значение. Графиката на функцията z=f(x;y) е определена повърхност. Графиката на функцията z=f(x 0 ;y 0) е пресечната линия на тази повърхност с равнината y=y 0. Въз основа на геометричния смисъл на производната за функция на една променлива, заключаваме, че f" x (x 0 ;y 0)=tgα, където α е ъгълът между оста Ox и допирателната, начертана към кривата z=f (x 0 ;y 0) в точка M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Подобно на f" y (x 0 ;y 0)=tgβ.
Билет №9
Тангентна равнина Нормално към повърхността
Билет №10
3. Изчисляване на определен интеграл по отсечка. Формула на Нютон-Лайбниц (извеждане).Ако функцията y=f(x) е непрекъсната на интервал и F(x) е някоя от нейните първоизводни върху (F"(x)=f(x)), тогава формулата ∫(от a до b) f( x) има )dx=F(b)-F(a). Тази формула е формулата на Нютон-Лайбниц. Помислете за идентичността: F(b)-F(a)=F(x n)-F(x 0)= (F(x n) -F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1) )-F(x 0)). Нека трансформираме всяка разлика в скоби, използвайки формулата на Лагранж: f(b)-f(a)=f'(c)*(b-a). Получаваме F(b)-F(a )=F'(c n)( x n -x n -1)+F'(c n -1)(x n -1 -x n -2)+F'(c 2)(x 2 -x 1)+F'(c 1)(x 1 -x 0 )= ΣF'(Ci)ΔXi=Σf(Ci)ΔXi, тоест F(b)-F(a)= Σf(Ci)ΔXi, където Ci е някаква точка от интервала (X i -1 ,X i). Тъй като функцията y=f(x) е непрекъсната върху , тогава тя е интегрируема върху . Следователно има граница на интегралната сума, равна на определения интеграл на f(x) Преминавайки към границата при λ=maxΔXi→0, получаваме F(b)-F( a)=lim Σf(Ci)ΔXi, тоест ∫(от a до b) f(x)dx=F( b)-F(a).
10. Дефиниция на диференцируема функция z=f(x;y) в точка. Дефиниция на пълен диференциал dz и неговата форма.Извиква се функцията z=f(x;y). диференцируемив точка M(x;y), ако общото му увеличение в тази точка може да бъде представено като: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, където α=α(∆ x;∆y)→0 и β=β(∆x;∆y)→0 за ∆x→0 и ∆y→0. Основната част от нарастването на функцията z=f(x;y), линейна спрямо ∆x и ∆y, се нарича пълен диференциалтази функция и се обозначава със символа dz: dz=A*∆x+B*∆y. dz=(δz/δx)dx+(δz/δy)dy.
Билет №11
4. Дефиниция на определен интеграл върху отсечка. Основни свойства на определен интеграл върху отсечка (с доказателство на едно от тях). Чрез определен интегралвърху сегмент от функция f(x), границата на интегралната сума Σf(c i)Δx i се извиква, ако тази граница съществува и не зависи нито от разделянето на сегмента на части, нито от избора на точки t във всяка от частите, при условие че дължината на най-големите частични сегменти (∆xi) клони към нула, т.е. ∫(от a до b) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Имоти: 1) Ако c е постоянно число и функцията f(x) е интегрируема върху , тогава ∫(от a до b) c*f(x)dx=c*∫(от a до b) f(x)dx .2) Ако функциите f 1 (x) b f 2 (x) са интегрируеми върху , тогава тяхната сума също е интегрируема ∫(от a до b) (f 1 (x)+f 2 (x))dx=∫( от a до b) f 1 (x)dx+∫(от a до b) f 2 (x)dx. 3)∫(от a до b) f(x)dx= -∫(от b до a) f(x)dx. 4)Ако функцията f(x) е интегрируема върху и a 10. Дефиниция на диференцируема функция z=f(x;y) в точка.Извиква се функцията z=f(x;y). диференцируемив точка M(x;y), ако общото му увеличение в тази точка може да бъде представено като: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, където α=α(∆ x;∆y)→0 и β=β(∆x;∆y)→0 за ∆x→0 и ∆y→0. 12. Свойство на диференцируема функция: връзка между диференцируемостта на функцията z=f(x,y) и наличието на частни производни в точка (формулировка, доказателство). Теорема: Ако една функция е диференцируема в точка, тогава в тази точка има крайни частични производни, A и B са числено равни Дадено е: Δz=AΔx+BΔy+0(ρ) Докажете: Ǝ(δz/δx(x 0 ; y 0)=A Доказателство: Нека дадем x 0 →Δx, y=y 0 =>Δ x z=(A*Δx+0(│x│). ρ=√(Δx 2 +Δy 2)=│Δx│. Δ x z/Δx=A +0(│x│)/Δx. LimΔx→0 (Δ x z/Δx)=lim=A. δz/Δx(x 0 ;y 0)=A. Аналогично: Y 0 →Δy, x=x 0 => Δ y Z. δz/Δy(x 0 ; y 0)=B. Билет №12 Доказателство 8. Частични нараствания на функцията z=f(x;y). Частични производни: определение и тяхното геометрично значение.Нека е дадена функцията z=f(x;y). Тъй като x и y са независими променливи, едната от тях може да се променя, докато другата остава постоянна. Нека дадем на променливата x увеличение ∆x, като запазим стойността на променливата y непроменена. Тогава функцията z ще получи увеличение, което ще извикаме частно увеличение z в x и означете ∆ x z. И така, ∆ x z=f(x+∆x;y)–f(x;y). По подобен начин получаваме частичното увеличение на z по отношение на y: ∆ y z=f(x;у+∆y)–f(x;y). Ако има ограничение lim∆x→0(∆ x z/∆x )=lim∆x→0( (f(x+∆x;y)-f(x;y))/∆x), тогава се нарича частична производнафункция z=f(x;y) в точката M(x;y) в променливата x и се означава с един от символите: z" x, δz/δx; f" x, δf/δx. Геометрично значение. Графиката на функцията z=f(x;y) е определена повърхност. Графиката на функцията z=f(x 0 ;y 0) е пресечната линия на тази повърхност с равнината y=y 0. Въз основа на геометричния смисъл на производната за функция на една променлива, заключаваме, че f" x (x 0 ;y 0)=tgα, където α е ъгълът между оста Ox и допирателната, начертана към кривата z=f (x 0 ;y 0) в точка M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Подобно на f" y (x 0 ;y 0)=tgβ. Билет №13 2. Проблемът за площта на криволинейния трапец, водещ до концепцията за определен интеграл върху сегмент. Определение на определен интеграл върху отсечка. Нека функцията y=f(x)≥0 е дадена на отсечката. Фигура, ограничена отгоре от графиката на функцията y=f(x), отдолу от оста Ox, а отстрани от прави линии x=a и x=b, се нарича криволинеен трапец. Нека намерим площта на този трапец. f(c 1)Δx 1 +f(c 2)Δx 2 +..+f(c n)Δx n =Σf(c i)Δx i =Sn. С намаляване на всички стойности на Δx i, точността на приближаването на криволинейния трапец със стъпаловидна фигура и точността на получената формула се увеличават. Следователно, за точната стойност на площта S на криволинейния трапец, ние приемаме границата S, към която площта на стъпаловидна фигура Sn клони, когато n нараства без ограничение, така че λ=maxΔx i →0: S=lim n →∞ Sn=lim n→∞(λ→0 ) Σf(c i)Δx i , тоест S=∫(от a до b) f(x)dx. И така, определеният интеграл на неопределена функция е числено равен на площта на криволинейния трапец , Ако интегралната сума Sn има граница I, която не зависи нито от метода за разделяне на сегмента на цифрови сегменти, нито от избор на точки в тях, то числото I се нарича определен интеграл на функцията y=f(x) върху отсечката и се означава с ∫(от a до b) f(x)dx. Така ∫(от a до b) f(x)dx=lim n→∞(λ→0) Σf(c i)Δx i . 17. Допирателна равнина и нормала към повърхността (дефиниция).Тангентна равнинакъм повърхност в точка M, равнина, минаваща през тази точка от повърхността, се нарича, ако ъгълът между тази равнина и секущата, минаваща през точка M и всяка друга точка M 1 от повърхността, клони към нула, както M клони към M 1. Нормално към повърхносттав точка M е права линия, минаваща през тази точка, перпендикулярна на допирателната равнина. 18. Уравнения на допирателната равнина и нормалата към неявно зададена повърхност.имплицитно. F(x;y;z) в точка Mo(Xo;Yo;Zo). K: (δF/δx)|M 0 (X-X 0)+(δF/δy)|M 0 (Y-Y 0)+(δF/δz)|M 0 (Z-Z 0)N: (X-X 0)/(δF/ δx)|M 0 =(Y-Y 0)/(δF/δy)|M 0 =(Z-Z 0)/(δF/δz)|M 0 Билет №14 5. Теорема за оценка на определен интеграл върху отсечка (формулировка, доказателство, геометричен смисъл). Оценка на интеграла. Ако m и M са съответно най-малката и най-голямата стойност на функцията y=f(x) на сегмента , (a 8. Частични нараствания на функцията z=f(x;y). Частични производни: определение и тяхното геометрично значение.Нека е дадена функцията z=f(x;y). Тъй като x и y са независими променливи, едната от тях може да се променя, докато другата остава постоянна. Нека дадем на променливата x увеличение ∆x, като запазим стойността на променливата y непроменена. Тогава функцията z ще получи увеличение, което ще извикаме частно увеличение z в x и означете ∆ x z. И така, ∆ x z=f(x+∆x;y)–f(x;y). По подобен начин получаваме частичното увеличение на z по отношение на y: ∆ y z=f(x;у+∆y)–f(x;y). Ако има ограничение lim∆x→0(∆ x z/∆x )=lim∆x→0( (f(x+∆x;y)-f(x;y))/∆x), тогава се нарича частична производнафункция z=f(x;y) в точката M(x;y) в променливата x и се означава с един от символите: z" x, δz/δx; f" x, δf/δx. Геометрично значение. Графиката на функцията z=f(x;y) е определена повърхност. Графиката на функцията z=f(x 0 ;y 0) е пресечната линия на тази повърхност с равнината y=y 0. Въз основа на геометричния смисъл на производната за функция на една променлива, заключаваме, че f" x (x 0 ;y 0)=tgα, където α е ъгълът между оста Ox и допирателната, начертана към кривата z=f (x 0 ;y 0) в точка M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Подобно на f" y (x 0 ;y 0)=tgβ. Билет №15 3. Изчисляване на определен интеграл по отсечка. Формула на Нютон-Лайбниц (извеждане).Ако функцията y=f(x) е непрекъсната на интервал и F(x) е някоя от нейните първоизводни върху (F"(x)=f(x)), тогава формулата ∫(от a до b) f( x) има )dx=F(b)-F(a). Тази формула е формулата на Нютон-Лайбниц. Помислете за идентичността: F(b)-F(a)=F(x n)-F(x 0)= (F(x n) -F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1) )-F(x 0)). Нека трансформираме всяка разлика в скоби, използвайки формулата на Лагранж: f(b)-f(a)=f'(c)*(b-a). Получаваме F(b)-F(a )=F'(c n)( x n -x n -1)+F'(c n -1)(x n -1 -x n -2)+F'(c 2)(x 2 -x 1)+F'(c 1)(x 1 -x 0 )= ΣF'(Ci)ΔXi=Σf(Ci)ΔXi, тоест F(b)-F(a)= Σf(Ci)ΔXi, където Ci е някаква точка от интервала (X i -1 ,X i). Тъй като функцията y=f(x) е непрекъсната върху , тогава тя е интегрируема върху . Следователно има граница на интегралната сума, равна на определения интеграл на f(x) Преминавайки към границата при λ=maxΔXi→0, получаваме F(b)-F( a)=lim Σf(Ci)ΔXi, тоест ∫(от a до b) f(x)dx=F( b)-F(a). 8. Частични нараствания на функцията z=f(x;y). Частични производни: определение и тяхното геометрично значение.Нека е дадена функцията z=f(x;y). Тъй като x и y са независими променливи, едната от тях може да се променя, докато другата остава постоянна. Нека дадем на променливата x увеличение ∆x, като запазим стойността на променливата y непроменена. Тогава функцията z ще получи увеличение, което ще извикаме частно увеличение z в x и означете ∆ x z. И така, ∆ x z=f(x+∆x;y)–f(x;y). По подобен начин получаваме частичното увеличение на z по отношение на y: ∆ y z=f(x;у+∆y)–f(x;y). Ако има ограничение lim∆x→0(∆ x z/∆x )=lim∆x→0( (f(x+∆x;y)-f(x;y))/∆x), тогава се нарича частична производнафункция z=f(x;y) в точката M(x;y) в променливата x и се означава с един от символите: z" x, δz/δx; f" x, δf/δx. Геометрично значение. Графиката на функцията z=f(x;y) е определена повърхност. Графиката на функцията z=f(x 0 ;y 0) е пресечната линия на тази повърхност с равнината y=y 0. Въз основа на геометричния смисъл на производната за функция на една променлива, заключаваме, че f" x (x 0 ;y 0)=tgα, където α е ъгълът между оста Ox и допирателната, начертана към кривата z=f (x 0 ;y 0) в точка M 0 (x 0 ;y 0 ;f(x 0 ;y 0)). Подобно на f" y (x 0 ;y 0)=tgβ. Билет №16 6. Теорема за средната стойност (формулировка, доказателство, геометричен смисъл).Ако функцията f(x) е непрекъсната на отсечката , тогава има точка C∈ такава, че ∫(от a до b) f(x)dx=f(c)*(b-a). Доказателство. Съгласно формулата на Нютон-Лайбниц имаме ∫(от a до b) f(x)dx=F(x)|(от a до b)=F(b)-F(a), където F"(x )=f( x). Прилагайки теоремата на Лагранж (теоремата за крайното нарастване на функция) към разликата F(b)-F(a), получаваме F(b)-F(a)=F"(c )*(b-a)=f(c) *(b-a). Геометрично значение. Теоремата за f(x)≥0 има просто геометрично значение: стойността на определения интеграл е равна за някои C∈ (a;b) на площта на правоъгълник с височина f(c) и основа б-а. Числото f(c)=1/(b-a)∫(от a до b) f(x)dx се нарича средна стойност на функцията f(x) върху сегмента. 21. Производна на функцията u=u(x;y;z) по посока l (определение).Границата LimΔl→0(Δu/Δl) се нарича производна на функцията u(x;y;z) по посока на вектора lв точка с координати (x;y;z). 22. Градиент на функцията u=u(x;y;z) в точка (дефиниция).Вектор с координати (δu/δx; δu/δy; δu/δz) се нарича Билет №17 7. Интеграл с променлива горна граница. Теорема за производната на интеграл с променлива горна граница (формулировка, доказателство). Производната на определен интеграл по отношение на горната граница на променлива е равна на интегралната функция, в която променливата за интегриране е заменена с тази граница, тоест (∫(от a до x) f(t)dt)" x =f (х). Доказателство. Според формулата на Нютон-Лайбниц имаме: ∫(от a до x) f(t)dt=F(t)|(от a до x)=F(x)-F(a). Следователно (∫(от a до x) f(t)dt)" x =(F(x)-F(a))" x =F"(x)-0=f(x). Това означава, че a определен интеграл с променлива горна граница е една от първоизводните на интегранта. пълно увеличение непрекъснато непрекъснато Билет №18 1. Антипроизводна функция. Теорема за разликата между две първоизводни (с доказателство). Неопределен интеграл: определение, най-прости свойства на неопределения интеграл (с доказателство за едно от тях). Извиква се функцията F(x). противопроизводна функция f(x) на интервала (a;b), ако за всяко x∈(a;b) е изпълнено равенството F"(x)=f(x). Теорема. Ако функцията F(x) е антипроизводна на функцията f(x) върху (a;b), тогава множеството от всички първоизводни за f(x) е дадено от формулата F(x)+C, където C= конст. Доказателство. Функцията F(x)+C е първоизводна на f(x). Наистина, (F(x)+C)"=F"(x)=f(x). Нека Ф(x) е друга първообразна функция f(x), различна от F(x), т.е. Ф"(x)=f(x). Тогава за всяко x∈(a;b) имаме (Ф(х)-F(x))"=Ф"(x)-F"(x)=f( x)-f(x)=0. А това означава, че Ф(х)-F(х)=C, C=const. Следователно Ф(x)=F(x)+C.Множеството от всички първообразни функции F(x)+C за f(x) се нарича неопределен интегрална функцията f(x) и се означава със символа ∫f(x)dx. Имоти: 1) Диференциалът на неопределения интеграл е равен на интегранта, а производната на неопределения интеграл е равен на интегранта d(∫f(x)dx)=f(x)dx, (∫f(x)dx )"=f(x).d (∫f(x)dx)=d(F(x)+C)=dF(x)+dC=F"(x)dx=f(x)dx. и (∫f(x)dx)"=(F(x)+C)"=F"(x)+0=f(x).2) Неопределеният интеграл на диференциала на някаква функция е равен на сумата на тази функция и произволна константа: ∫dF(x)=F(x)+C.∫dF(x)=F"(x)dx=∫f(x)dx=F(x)+C.3) Постоянният фактор може да бъде изваден от знака за интеграл: ∫af(x)dx=a∫f(x)dx.4) Неопределеният интеграл на алгебричната сума на краен брой непрекъснати функции е равен на алгебричната сума на интегралите от събираемите на функциите: ∫(f(x)±g(x))dx=∫f (x)dx±∫g(x)dx.5) (Инвариантност на формулата за интегриране). Ако ∫f(x)dx=F(x)+C, тогава ∫f(u)du=F(u)+C, където u=φ(x) е произволна функция с непрекъсната производна. 22. Градиент на функцията u=u(x;y;z) в точка (дефиниция, свойства). Връзка между производна по посока и градиент на функция (обосновка). Вектор с координати (δu/δx; δu/δy; δu/δz) се нарича градиент на функцията u=f(x;y;z)и се означава с gradU=(δu/δx; δu/δy; δu/δz). gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Имоти: 1)gradC=0; 2)grad(c*u)=c*gradU; 3)grad(u+v)=gradU+gradV; 4)grad(u*v)=u*gradV+v*gradU, където u*v са скаларни произведения на вектори u и v. Връзка. Нека са дадени функцията u=u(x;y;z) и градиентното поле gradU=(δu/δx)*i+(δu/δy)*j+(δu/δz)*k. Тогава производната Δu/Δl по посока на някакъв вектор l е равна на проекцията на вектора GradU върху вектора l. Билет №19 4. Дефиниция на определен интеграл върху отсечка. Основни свойства на определен интеграл върху отсечка (с доказателство на едно от тях). Чрез определен интегралвърху сегмент от функция f(x), границата на интегралната сума Σf(c i)Δx i се извиква, ако тази граница съществува и не зависи нито от разделянето на сегмента на части, нито от избора на точки t във всяка от частите, при условие че дължината на най-големите частични сегменти (∆xi) клони към нула, т.е. ∫(от a до b) f(x)dx=lim Δx i →0 Σf(c i)Δx i . Имоти: 1) Ако c е постоянно число и функцията f(x) е интегрируема върху , тогава ∫(от a до b) c*f(x)dx=c*∫(от a до b) f(x)dx . Доказателство.Нека съставим интегралната сума за функцията c*f(x). Имаме Σс*f(c i)Δx i =с*Σf(c i)Δx i . Тогава lim n→∞ Σс*f(c i)Δx i =c*lim n→∞ f(c i)=с*∫(от a до b) f(x)dx. От това следва, че функцията с*f(x) е интегрируема върху и формулата ∫(от a до b) с*f(x)dx= с*∫(от a до b) f(x)dx.2) Ако функциите f 1 (x) b f 2 (x) са интегрируеми върху , тогава тяхната сума е интегрируема и ∫(от a до b) (f 1 (x)+f 2 (x))dx=∫(от a до b ) f 1 (x)dx+∫(от a до b) f 2 (x)dx. 3)∫(от a до b) f(x)dx= -∫(от b до a) f(x)dx. 4)Ако функцията f(x) е интегрируема върху и a 17. Допирателна равнина и нормала към повърхността (дефиниция). Теорема за съществуването на допирателна равнина (формулировка, доказателство). Тангентна равнинакъм повърхност в точка M, равнина, минаваща през тази точка от повърхността, се нарича, ако ъгълът между тази равнина и секущата, минаваща през точка M и всяка друга точка M 1 от повърхността, клони към нула, както M клони към M 1. Нормално към повърхносттав точка M е права линия, минаваща през тази точка, перпендикулярна на допирателната равнина. Теорема. Ако δF/δx; δF/δy; δF/δz са определени в околността на точката Mo и са непрекъснати в самата точка M 0 и в същото време не изчезват, тогава всички допирателни към линиите на повърхността лежат в една и съща равнина. Доказателство. L: система (x=x(t); y=y(t); z=z(t)). Допирателна (M 0 ;P) y=(x"(t 0); y"(t o); z"(t 0)). L∈Q (повърхност). F(x(t), y(t) , z(t))=0 е комплексна функция на променливата t. Използваме правилото за диференцируемост на комплексна функция: (δF/δx)*(dx/dt)+(δF/δy)*(dy/dt )+(δF/δz)*( dz/dt)=0; (δF(M 0)/δx)*x"(t 0)+(δF(M 0)/δy)*y"(t 0)+ (δF(M 0)/δz) *z"(t 0)=0; g=(x"(t 0),y"(t 0),z"(t 0)); означаваме n=(δF(M 0)/δx; δF(M 0)/δy; δF(M 0) /δz); n⊥g. Тъй като през дадена точка могат да бъдат начертани безкраен брой прави, лежащи на повърхността, и безкраен брой допирателни към тях, следователно всички допирателни линии лежат в една и съща равнина. Билет №20 6. Теорема за средната стойност (формулировка, доказателство, геометричен смисъл).Ако функцията f(x) е непрекъсната на отсечката , тогава има точка C∈ такава, че ∫(от a до b) f(x)dx=f(c)*(b-a). Доказателство. Съгласно формулата на Нютон-Лайбниц имаме ∫(от a до b) f(x)dx=F(x)|(от a до b)=F(b)-F(a), където F"(x )=f( x). Прилагайки теоремата на Лагранж (теоремата за крайното нарастване на функция) към разликата F(b)-F(a), получаваме F(b)-F(a)=F"(c )*(b-a)=f(c) *(b-a). Геометрично значение. Теоремата за f(x)≥0 има просто геометрично значение: стойността на определения интеграл е равна за някои C∈ (a;b) на площта на правоъгълник с височина f(c) и основа б-а. Числото f(c)=1/(b-a)∫(от a до b) f(x)dx се нарича средна стойност на функцията f(x) върху сегмента. 9. Пълно нарастване на функцията z=f(x;y). Непрекъснатост на функцията z=f(x;y) в точка (две определения).Нека е дадена функцията z=f(x;y). Нека дадем на независимата променлива x увеличение ∆x и на променливата y увеличение ∆y. Тогава пълно увеличение∆z на функцията се определя от равенството: ∆z=f(x+∆x;y+∆y)-f(x;y). 1) Извиква се функцията z=f(x;y). непрекъснатов точката M 0 (x 0 ;y 0)∈ D(z), ако нейната граница в тази точка съвпада със стойността на функцията в тази точка, т.е. limX→X 0 \Y→Y 0 (f(x;y))= f(x 0;y 0). 2) Функция z=f(x;y) непрекъснатовърху множество, ако е непрекъснато във всяка точка от това множество Билет №21 5. Теорема за оценка на определен интеграл върху отсечка (формулировка, доказателство, геометричен смисъл). Оценка на интеграла. Ако m и M са съответно най-малката и най-голямата стойност на функцията y=f(x) на сегмента , (a 21. Производна на функцията u=u(x;y;z) по посока l (дефиниция, формула за изчисление, извеждане на изчислителната формула). Границата LimΔl→0(Δu/Δl) се нарича производна на функцията u(x;y;z) по посока на вектора lв точка с координати (x;y;z).Δu/Δl=LimΔl→0(Δl u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ Да предположим, че функцията u(x;y;z) е непрекъсната и има непрекъснати производни по отношение на своите аргументи в областта D: Δu=(δu/δx)Δx+(δu/δy)Δy+(δu/δz)Δz+ E 1 Δx+E 2 Δy+E 3 Δz, където E 1, E 2, E 3 клонят към нула като Δl→0. Нека разделим цялото равенство на Δl. Δu/Δl=(δu/δx)(Δx/Δl)+(δu/δy)(Δy/Δl)+(δu/δz)(Δz/Δl)+E 1 (Δx/Δl)+E 2 (Δy/ Δl)+E 3 (Δz/Δl). Δx/Δl=cosα; Δy/Δl=cosβ; Δz/Δl=cosγ. Равенството може да бъде представено по следния начин: Δu/Δl=(δu/δx)cosα+(δu/δy)cosβ+(δu/δz)cosγ+E 1 cosα+E 2 cosβ+E 3 cosγ. Придвижвайки се до границата, получаваме Δu/Δl=LimΔl→0(Δl u/Δl)=(δu/δx)*cosα+(δu/δy)*cosβ+(δu/δz)*cosγ. Билет №22 3. Изчисляване на определен интеграл по отсечка. Формула на Нютон-Лайбниц (извеждане).Ако функцията y=f(x) е непрекъсната на интервал и F(x) е някоя от нейните първоизводни върху (F"(x)=f(x)), тогава формулата ∫(от a до b) f( x) има )dx=F(b)-F(a). Тази формула е формулата на Нютон-Лайбниц. Помислете за идентичността: F(b)-F(a)=F(x n)-F(x 0)= (F(x n) -F(x n -1))+(f(x n -1)-F(x n -2))+…(F(x 2)-F(x 1))+(F(x 1) )-F(x 0)). Нека трансформираме всяка разлика в скоби, използвайки формулата на Лагранж: f(b)-f(a)=f'(c)*(b-a). Получаваме F(b)-F(a )=F'(c n)( x n -x n -1)+F'(c n -1)(x n -1 -x n -2)+F'(c 2)(x 2 -x 1)+F'(c 1)(x 1 -x 0 )= ΣF'(Ci)ΔXi=Σf(Ci)ΔXi, тоест F(b)-F(a)= Σf(Ci)ΔXi, където Ci е някаква точка от интервала (X i -1 ,X i). Тъй като функцията y=f(x) е непрекъсната върху , тогава тя е интегрируема върху . Следователно има граница на интегралната сума, равна на определения интеграл на f(x) Преминавайки към границата при λ=maxΔXi→0, получаваме F(b)-F( a)=lim Σf(Ci)ΔXi, тоест ∫(от a до b) f(x)dx=F( b)-F(a). 19. Определяне на точките на максимум и минимум на функцията z=f(x,y).Точката (X 0 ; Y 0) се нарича максимална точкафункция z=f(x;y), ако има δ-околност на точката (X 0 ;Y 0), така че неравенството f(x;y) е в сила 20. Достатъчен признак за съществуването на екстремум на функцията z=f(x;y). (формулировка).Нека в стационарна точка (X 0 ;Y 0) и част от нейната околност функцията f(x;y) има непрекъснати частни производни до втори ред включително. Нека изчислим в точката (X 0 ;Y 0) стойностите A=f"" xx (X 0 ;Y 0), B=f"" xy (X 0 ;Y 0), C=f"" yy (X 0 ; Y 0). Нека означим Δ=|AB; BC|=AC-B^2. Тогава: 1) ако Δ>0, тогава функцията f(x;y) в точката (X 0 ;Y 0) има екстремум: максимум, ако A<0; минимум, если A>0; 2) ако Δ<0, то функция f(x;y) в точке (X 0 ;Y 0) экстремума не имеет. В случае Δ=0 экстремум в точке (X 0 ;Y 0) может быть, а может не быть. Необходимы дополнительные исследования. Билет №23 2. Проблемът за площта на криволинейния трапец, водещ до концепцията за определен интеграл върху сегмент. Определение на определен интеграл върху отсечка. Нека функцията y=f(x)≥0 е дадена на отсечката. Фигура, ограничена отгоре от графиката на функцията y=f(x), отдолу от оста Ox, а отстрани от прави линии x=a и x=b, се нарича криволинеен трапец. Нека намерим площта на този трапец. f(c 1)Δx 1 +f(c 2)Δx 2 +..+f(c n)Δx n =Σf(c i)Δx i =Sn. С намаляване на всички стойности на Δx i, точността на приближаването на криволинейния трапец със стъпаловидна фигура и точността на получената формула се увеличават. Следователно, за точната стойност на площта S на криволинейния трапец, ние приемаме границата S, към която площта на стъпаловидна фигура Sn клони, когато n нараства без ограничение, така че λ=maxΔx i →0: S=lim n →∞ Sn=lim n→∞(λ→0 ) Σf(c i)Δx i , тоест S=∫(от a до b) f(x)dx. И така, определеният интеграл на неопределена функция е числено равен на площта на криволинейния трапец , Ако интегралната сума Sn има граница I, която не зависи нито от метода за разделяне на сегмента на цифрови сегменти, нито от избор на точки в тях, то числото I се нарича определен интеграл на функцията y=f(x) върху отсечката и се означава с ∫(от a до b) f(x)dx. Така ∫(от a до b) f(x)dx=lim n→∞(λ→0) Σf(c i)Δx i . 17. Допирателна равнина към повърхнина (дефиниция).Тангентна равнинакъм повърхност в точка M, равнина, минаваща през тази точка от повърхността, се нарича, ако ъгълът между тази равнина и секущата, минаваща през точка M и всяка друга точка M 1 от повърхността, клони към нула, както M клони към M 1. 18. Уравнения на допирателна равнина към изрично зададена повърхносточевидно. z=f(x;y) в точка Mo(Xo;Yo;Zo). K: (δz/δx)|M 0 (X-X 0)+(δz/δy)|M 0 (Y-Y 0)-(Z-Z 0)=0 Билет №24 6. Теорема за средната стойност (формулировка, доказателство, геометричен смисъл).Ако функцията f(x) е непрекъсната на отсечката , тогава има точка C∈ такава, че ∫(от a до b) f(x)dx=f(c)*(b-a). Доказателство. Съгласно формулата на Нютон-Лайбниц имаме ∫(от a до b) f(x)dx=F(x)|(от a до b)=F(b)-F(a), където F"(x )=f( x). Прилагайки теоремата на Лагранж (теоремата за крайното нарастване на функция) към разликата F(b)-F(a), получаваме F(b)-F(a)=F"(c )*(b-a)=f(c) *(b-a). Геометрично значение. Теоремата за f(x)≥0 има просто геометрично значение: стойността на определения интеграл е равна за някои C∈ (a;b) на площта на правоъгълник с височина f(c) и основа б-а. Числото f(c)=1/(b-a)∫(от a до b) f(x)dx се нарича средна стойност на функцията f(x) върху сегмента. 10. Дефиниция на диференцируема функция z=f(x;y) в точка.Извиква се функцията z=f(x;y). диференцируемив точка M(x;y), ако общото му увеличение в тази точка може да бъде представено като: ∆z=A*∆x+B*∆y+α*∆x+β*∆y, където α=α(∆ x;∆y)→0 и β=β(∆x;∆y)→0 за ∆x→0 и ∆y→0. 12. Свойство на диференцируема функция: връзка между диференцируемостта на функцията z=f(x,y) и наличието на частни производни в точка (формулировка, доказателство). Теорема: Ако една функция е диференцируема в точка, тогава в тази точка има крайни частични производни, A и B са числено равни Дадено е: Δz=AΔx+BΔy+0(ρ) Докажете: Ǝ(δz/δx(x 0 ; y 0)=A Доказателство: Нека дадем x 0 →Δx, y=y 0 =>Δ x z=(A*Δx+0(│x│). ρ=√(Δx 2 +Δy 2)=│Δx│. Δ x z/Δx=A +0(│x│)/Δx. LimΔx→0 (Δ x z/Δx)=lim=A. δz/Δx(x 0 ;y 0)=A. Аналогично: Y 0 →Δy, x=x 0 => Δ y Z. δz/Δy(x 0 ;y 0)=B Първият достатъчен знак за екстремум се формулира на базата на промяна в знака на първата производна при преминаване през критичната точка. Вторият признак на екстремум ще бъде разгледан по-долу в § 6.4. Теорема (първи знак за екстремум)
:
Акох 0
– критична точка на функциятаy=f(х)
и в някакъв квартал на точкатах 0
, преминавайки през него отляво надясно, производната променя знака на противоположния, тогавах 0
е екстремната точка. Освен това, ако знакът на производната се промени от "+" на "-", тогавах 0
е максималната точка иf(х 0
)
– максимумът на функцията и ако производната смени знака от „-“ на „+“, тогавах 0
е минималната точка иf(х 0
)
– минимална функция. Разглежданият екстремум е местен(локален) характер и засяга някои малки околности на критичната точка. Точките на екстремум и точките на прекъсване разделят областта на дефиниране на функция на интервали на монотонност. Пример 6.3.В пример 6.1. открихме критични точки х 1
=0
И х 2
=2.
Нека разберем дали функцията е валидна в тези точки y=2x 3
-6x 2
+1
има екстремум. Нека заместим в неговата производна Да се намери най-голямата и най-малката стойност на непрекъсната функция върху отсечка Графиката на диференцируема функция се наричаизпъкнална интервал, ако се намира под някоя от неговите допирателни на този интервал;вдлъбнат (изпъкнал надолу), ако се намира над всяка допирателна на интервала. а) Необходими знаци Ако графиката на функцияy=f(х)
изпъкнал
на интервала(а,
b)
, след това втората производна П Ако графиката на функция вдлъбнатНа (а,
b)
, тогава, разсъждавайки по подобен начин, виждаме, че когато допирателната се плъзга по кривата (фиг. 6.3b), ъгълът на наклона на допирателната се увеличава ( b Ако за функциятаy=f(х)
във всички точки на някакъв интервал ще има "Правило на дъжда"
:
За да запомните кой знак на втората производна да свържете с изпъкнала и кой с вдлъбната дъга на графиката, препоръчваме да запомните: „плюс вода“
във вдлъбнат отвор, „минус вода“ - в изпъкнал отвор (фиг. 6.4). Точката в графиката на непрекъсната функция, в която изпъкналостта се променя на вдлъбнатост или обратно, се наричаинфлексна точка
. Теорема (достатъчен признак за съществуването на инфлексна точка). Ако
в точката Точките, в които втората производна изчезва или не съществува, се наричат критични точки от втори род. Пример 6.4.Намерете точките на инфлексия и определете интервалите на изпъкналост и вдлъбнатост на кривата Р За да намерите максимума и минимума на функция, можете да използвате всеки от трите достатъчни признака на екстремум. Въпреки че най-често срещаният и удобен е първият. Първото достатъчно условие за екстремум. Нека функцията y = f(x)е диференцируем в -околост на точката и е непрекъснат в самата точка. Тогава С други думи: Алгоритъм. Намираме производната на функцията в областта на дефиниция. Определяме нулите на числителя, нулите на знаменателя на производната и точките от областта на дефиниция, в които производната не съществува (тези точки се наричат точки на възможен екстремум, преминавайки през тези точки, производната може просто да промени знака си). Тези точки разделят областта на дефиниране на функцията на интервали, в които производната запазва своя знак. Определяме знаците на производната на всеки от интервалите (например, като изчисляваме стойността на производната на функция във всяка точка от определен интервал). Избираме точки, в които функцията е непрекъсната и при преминаване през които производната променя знака. Пример.Намерете екстремумите на функцията. Нулите на числителя са точки х = -1И х = 5, знаменателят отива на нула при х = 2. Маркирайте тези точки върху числовата ос Определяме знаците на производната на всеки интервал; за да направим това, изчисляваме стойността на производната във всяка от точките на всеки интервал, например в точките x = -2, x = 0, x = 3И х=6. Следователно на интервала производната е положителна (на фигурата поставяме знак плюс над този интервал). По същия начин Затова поставяме минус над втория интервал, минус над третия и плюс над четвъртия. Остава да изберем точки, в които функцията е непрекъсната и нейната производна променя знака. Това са точките на екстремума. Отговор: . Вторият достатъчен признак за екстремум на функция. ако , тогава е минималната точка; ако , тогава е максималната точка. Както можете да видите, този критерий изисква наличието на производна поне до втория ред в точката. Следователно, чрез второто достатъчно условие за екстремум, х = 1- максимална точка. След това - максимумът на функцията. Отговор: . Край на работата - Тази тема принадлежи към раздела: Концепцията за матрица е операции върху матрици и техните свойства.. матрицата е правоъгълна таблица, съставена от числа, които не могат да бъдат.. и събирането на матрици е елементна операция.. Ако имате нужда от допълнителен материал по тази тема или не сте намерили това, което търсите, препоръчваме да използвате търсенето в нашата база данни с произведения: Ако този материал е бил полезен за вас, можете да го запазите на страницата си в социалните мрежи: Определение за диференцируемост Правило за диференциране Геометрично значение на производната. Уравнение на тангенс Геометричен смисъл на производната на функция в точка Решение Необходими условия за екстремум и достатъчни условия за екстремум Условия за монотонност и постоянство на функция Определение за антипроизводно Преглед Първоизводната на произведението на константа и функция е равна на произведението на константа и първоизводната на функция Определение Геометрично значение Свойства на определен интеграл Формула на Нютон-Лайбниц (с доказателство) Екстремалната точка на функция е точката в областта на дефиниране на функцията, в която стойността на функцията приема минимална или максимална стойност. Стойностите на функцията в тези точки се наричат екстремуми (минимум и максимум) на функцията. Определение. Точка х1
функционална област f(х) е наречен максимална точка на функцията
, ако стойността на функцията в тази точка е по-голяма от стойностите на функцията в точки, достатъчно близки до нея, разположени отдясно и отляво на нея (т.е. неравенството е в сила f(х0
) > f(х 0
+ Δ х)
х1
максимум. Определение. Точка х2
функционална област f(х) е наречен минимална точка на функцията, ако стойността на функцията в тази точка е по-малка от стойностите на функцията в точки, достатъчно близки до нея, разположени отдясно и отляво на нея (т.е. неравенството е в сила f(х0
) < f(х 0
+ Δ х)
). В този случай казваме, че функцията има в точката х2
минимум. Да кажем точка х1
- максимална точка на функцията f(х) . След това в интервала до х1
функцията се увеличава, следователно производната на функцията е по-голяма от нула ( f "(х) > 0 ), и в интервала след х1
функцията намалява, следователно, производна на функцияпо-малко от нула ( f "(х) < 0
).
Тогда в точке х1
Нека приемем също, че точката х2
- минимална точка на функцията f(х) . След това в интервала до х2
функцията е намаляваща и производната на функцията е по-малка от нула ( f "(х) < 0
), а в интервале
после х2
функцията нараства и производната на функцията е по-голяма от нула ( f "(х) > 0 ). В този случай също в точката х2
производната на функцията е нула или не съществува. Теорема на Ферма (необходим знак за съществуването на екстремум на функция). Ако точката х0
- екстремна точка на функцията f(х), тогава в тази точка производната на функцията е равна на нула ( f "(х) = 0 ) или не съществува. Определение. Точките, в които производната на дадена функция е нула или не съществува, се наричат критични точки
. Пример 1.Нека разгледаме функцията. В точката х= 0 производната на функцията е нула, следователно точката х= 0 е критичната точка. Въпреки това, както може да се види на графиката на функцията, тя нараства в цялата област на дефиниция, така че точката х= 0 не е екстремната точка на тази функция. По този начин условията, че производната на функция в точка е равна на нула или не съществува, са необходими условия за екстремум, но не са достатъчни, тъй като могат да бъдат дадени други примери за функции, за които тези условия са изпълнени, но функцията няма екстремум в съответната точка. Ето защо трябва да има достатъчно доказателства, което позволява да се прецени дали има екстремум в дадена критична точка и какъв е екстремумът – максимален или минимален. Теорема (първият достатъчен признак за съществуването на екстремум на функция).Критична точка х0
f(х) ако при преминаване през тази точка производната на функцията промени знака и ако знакът се промени от "плюс" на "минус", тогава това е максимална точка, а ако от "минус" на "плюс", тогава това е минимална точка. Ако е близо до точката х0
, вляво и вдясно от нея, производната запазва знака си, това означава, че функцията или само намалява, или само нараства в определена околност на точката х0
. В този случай в точката х0
няма крайност. Така, за да определите екстремалните точки на функцията, трябва да направите следното
: Пример 2.Намерете екстремумите на функцията Решение. Нека намерим производната на функцията: Нека приравним производната на нула, за да намерим критичните точки: Тъй като за всякакви стойности на "x" знаменателят не е равен на нула, ние приравняваме числителя на нула: Имам една критична точка х= 3 . Нека определим знака на производната в интервалите, ограничени от тази точка: в диапазона от минус безкрайност до 3 - знак минус, тоест функцията намалява, в интервала от 3 до плюс безкрайност има знак плюс, тоест функцията нараства. Тоест точка х= 3 е минималната точка. Нека намерим стойността на функцията в минималната точка: Така се намира екстремната точка на функцията: (3; 0) и тя е минималната точка. Теорема (вторият достатъчен признак за съществуването на екстремум на функция).Критична точка х0
е екстремната точка на функцията f(х), ако втората производна на функцията в тази точка не е равна на нула ( f ""(х) ≠ 0 ), и ако втората производна е по-голяма от нула ( f ""(х) > 0 ), тогава максималната точка и ако втората производна е по-малка от нула ( f ""(х) < 0
),
то точкой минимума. Забележка 1. Ако в точката х0
Ако и първата, и втората производни са нулеви, тогава в този момент е невъзможно да се прецени наличието на екстремум въз основа на втория достатъчен критерий. В този случай трябва да използвате първия достатъчен критерий за екстремума на функция. Забележка 2. Вторият достатъчен критерий за екстремум на функция не е приложим дори когато първата производна не съществува в стационарна точка (тогава втората производна също не съществува). В този случай трябва да използвате и първия достатъчен знак за екстремум на функция. От горните дефиниции следва, че екстремумът на функцията е локален по природа - това е най-голямата и най-малката стойност на функцията в сравнение с близките стойности. Да приемем, че разглеждате приходите си за период от една година. Ако през май сте спечелили 45 000 рубли, а през април 42 000 рубли и през юни 39 000 рубли, тогава приходите от май са максимумът на функцията за печалба в сравнение с близките стойности. Но през октомври сте спечелили 71 000 рубли, през септември 75 000 рубли, а през ноември 74 000 рубли, така че приходите през октомври са минимумът на функцията за печалба в сравнение с близките стойности. И лесно можете да видите, че максимумът сред стойностите на април-май-юни е по-малък от минимума на септември-октомври-ноември. Най-общо казано, на интервал една функция може да има няколко екстремума и може да се окаже, че някакъв минимум на функцията е по-голям от всеки максимум. И така, за функцията, показана на фигурата по-горе, . Тоест, не трябва да се мисли, че максимумът и минимумът на функцията са съответно нейните най-големи и най-малки стойности в целия разглеждан сегмент. В максималната точка функцията има най-голяма стойност само в сравнение с онези стойности, които има във всички точки, достатъчно близки до максималната точка, а в минималната точка има най-малка стойност само в сравнение с тези стойности че има във всички точки достатъчно близо до минималната точка. Следователно можем да изясним горната концепция за екстремни точки на функция и да наречем минималните точки локални минимални точки, а максималните точки локални максимални точки. Пример 3. Решение: Функцията е дефинирана и непрекъсната на цялата числова ос. Негова производна За интервала контролната точка може да бъде: намери. Като вземем точка от интервала, получаваме, и вземем точка от интервала, имаме. И така, в интервалите и , и в интервала . Според първия достатъчен критерий за екстремум в точката няма екстремум (тъй като производната запазва знака си в интервала), а в точката функцията има минимум (тъй като производната променя знака от минус на плюс при преминаване през тази точка). Нека намерим съответните стойности на функцията: , a . В интервала функцията намалява, тъй като в този интервал , а в интервала нараства, тъй като в този интервал . За да изясним конструкцията на графиката, намираме нейните точки на пресичане с координатните оси. Когато получим уравнение, чиито корени са и , т.е. се намират две точки (0; 0) и (4; 0) от графиката на функцията. Използвайки цялата получена информация, изграждаме графика (вижте началото на примера). За самопроверка по време на изчисления можете да използвате онлайн деривативен калкулатор . Пример 4.Намерете екстремума на функцията и изградете нейната графика. Областта на дефиниране на функция е цялата числова ос, с изключение на точката, т.е. . За да съкратите изследването, можете да използвате факта, че тази функция е четна, тъй като Намиране на производната 1) 2) но функцията претърпява прекъсване в тази точка, така че не може да бъде точка на екстремум. Така дадената функция има две критични точки: и . Като вземем предвид четността на функцията, ще проверим само точката, използвайки втория достатъчен критерий за екстремум. За да направим това, намираме втората производна За да получите по-пълна картина на графиката на функция, нека разберем нейното поведение в границите на домейна на дефиниция: (тук символът показва желанието хдо нула от дясно, и хостава положителен; по подобен начин означава стремеж хдо нула отляво и хостава отрицателна). По този начин, ако , тогава . След това намираме тези. ако , тогава . Графиката на функцията няма пресечни точки с осите. Картината е в началото на примера. За самопроверка по време на изчисления можете да използвате онлайн деривативен калкулатор . Пример 8.Намерете екстремумите на функцията. Решение. Нека намерим областта на дефиниция на функцията. Тъй като неравенството трябва да бъде изпълнено, получаваме от . Нека намерим първата производна на функцията. Признаци на локално повишаване и намаляване на функцията. Една от основните задачи при изучаването на функция е да се намерят интервалите на нейното нарастване и намаляване. Такова изследване може лесно да се проведе с помощта на производното. Нека формулираме съответните твърдения. Необходими и достатъчни условия за съществуване на екстремум на функция в точка. Функцията g(x) в точка има екстремум (максимум или минимум), ако функцията е дефинирана в двустранна околност на точката и за всички точки x от някакъв регион: неравенството е изпълнено съответно (в случай на максимум) или (в случай на минимум). Екстремумът на функцията може да се намери от условието: ако производната съществува, т.е. приравняваме първата производна на функцията на нула. 1) Първо достатъчно условие: а) f(x) е непрекъсната функция и е дефинирана в някаква околност на точка, така че първата производна в тази точка е равна на нула или не съществува. b) f(x) има крайна производна в близост до спецификацията и непрекъснатост на функцията в) производната запазва определен знак отдясно на точка и отляво на същата точка, тогава точката може да се характеризира, както следва Това условие не е много удобно, тъй като трябва да проверите много условия и да запомните таблицата, но ако нищо не се казва за производни от по-висок ред, тогава това е единственият начин да намерите екстремума на функцията. 2) Второ достатъчно условие Ако функцията g(x) има втора производна и в даден момент първата производна е равна на нула, а втората производна е различна от нула. След това точка екстремум на функцията g(x), и ако , тогава точката е максимум; ако , тогава точката е минимум.
стойности х, взети отляво и отдясно на точката х 1
=0
в доста близка близост, напр. х=-1И х=1. ще получим. Тъй като производната променя знака от "+" на "-", тогава х 1
=0
е максималната точка и максимумът на функцията 
. Сега нека вземем две стойности x=1 и х=3от близост до друга критична точка х 2
=2
. Вече беше показано, че 
, А 
. Тъй като производната променя знака от „-“ на „+“, тогава х 2
=2
– минимална точка. И минималната функция 
.
трябва да изчислите стойността му във всички критични точки и в краищата на сегмента и след това да изберете най-големия и най-малкия от тях.6.3. Признаци за изпъкналост и вдлъбнатост на графика на функция. Инфлексни точки
6.3.1. Необходими и достатъчни признаци за изпъкналост и вдлъбнатост на графика
на този интервал; ако графикътвдлъбнат
На(а,
b)
, Че 
На(а,
b)
.
начертайте графика на функция y=f(х)
изпъкнал (а,
b)
(фиг. 6.3а). Ако допирателната се плъзга по изпъкнала крива отляво надясно, тогава нейният ъгъл на наклон намалява ( 
), в същото време ъгловият коефициент на тангенса също намалява, което означава, че първата производна намалява 
На (а,
b)
. Но тогава производната на първата производна като производна на намаляваща функция трябва да е отрицателна, т.е. 
На (а,
b)
.
), ъгловият коефициент нараства заедно с него, а оттам и производната. И тогава производната на производната като нарастваща функция трябва да е положителна, т.е 
На (а,
b)
.
) Достатъчни знаци
, след това графиката на функциятавдлъбнат
на този интервал и ако 
, Чеизпъкнал
.
функция 
е два пъти диференцируема и втората производна в тази точка е равна на нула или не съществува и ако при преминаване през точката 
втора производна 
променя знака, след това точка 
има инфлексна точка. Координати на инфлексна точка 
.
(крива на Гаус).
решение.Намираме първата и втората производни: 
,. Втората производна съществува за всеки 
. Приравняваме го на нула и решаваме полученото уравнение 
, Където 
, Тогава 
, където 
,
- критични точки от втори род. Нека проверим промяната в знака на втората производна при преминаване през критичната точка 
. Ако 
, Например, 
, Че 
, и ако 
, Например, 
, Че 
, тоест втората производна променя знака. следователно 
- абсцисата на инфлексната точка, нейните координати 
. Поради паритета на функцията 
, точка 
, симетричен на точката 
, също ще бъде инфлексна точка.
Решение.
Домейнът на функция е цялото множество от реални числа, с изключение на х = 2.
Намиране на производната:
В точката х = -1функцията е непрекъсната и производната променя знака от плюс на минус, следователно, според първия знак на екстремума, х = -1е максималната точка; на нея съответства максимумът на функцията.
В точката х = 5функцията е непрекъсната и производната променя знака от минус на плюс, следователно, х = -1е минималната точка; на нея съответства минимумът на функцията.
Графична илюстрация.
Позволявам ,
Пример.Намерете екстремумите на функцията.
Решение.
Нека започнем с домейна на дефиницията:
Нека разграничим оригиналната функция:
Производната отива на нула при х = 1, тоест това е точка на възможен екстремум.
Намираме втората производна на функцията и изчисляваме нейната стойност при х = 1:
Графична илюстрация.
Третият достатъчен признак за екстремум на функция.
Нека функцията y = f(x)има производни до н-ти ред в -околността на точката и производни до n+1-ти ред в самата точка. Нека бъде.
Тогава,Алгебра и аналитична геометрия. Понятие за матрица, операции върху матрици и техните свойства
Какво ще правим с получения материал:
Tweet
Всички теми в този раздел:
Операцията за намиране на производната се нарича диференциране на функция. За една функция се казва, че е диференцируема в дадена точка, ако има крайна производна в тази точка, и
Следствие 1. Постоянният множител може да бъде изваден от знака на производната:
Ъгълът на наклона на права линия y = kx+b е ъгълът, измерен от позицията
Нека разгледаме секанса AB на графиката на функцията y = f(x), така че точките A и B имат съответно координати
Функцията е дефинирана за всички реални числа. Тъй като (-1; -3) е точка на допиране, тогава
Дефиниция на нарастваща функция. Функцията y = f(x) нараства на интервала X, ако за всеки
Условие за (нестрога) монотонност на функция върху интервал. Нека функцията има производна във всяка
Първоизводна на функция f(x) на интервала (a; b) е функция F(x), такава че равенството
За да проверим резултата, диференцираме получения израз: В резултат на това получаваме
Достатъчно условие за съществуването на първоизводна на функция, дадена на интервал, е
Нека се дефинира на
Определеният интеграл е числено равен на площта на фигурата, ограничена от абсцисната ос и правите линии
Основни свойства на определен интеграл. Свойство 1. Производната на определен интеграл по отношение на горната граница е равна на подинтегралната функция, в която вместо променлива е интегрирана
Формула на Нютон-Лайбниц. Нека функцията y = f(x) е непрекъсната на интервал и F(x) е една от първопроизводните на функцията на този интервал, тогава уравнението
.
.Локален характер на екстремумите на функцията
Търсим заедно екстремума на функцията
също съществува на цялата числова ос. Следователно в случая критичните точки са само тези, при които, т.е. , от къде и . Критични точки и разделят цялата област на дефиниране на функцията на три интервала на монотонност: . Нека изберем по една контролна точка във всяка от тях и да намерим знака на производната в тази точка.
. Следователно неговата графика е симетрична спрямо оста Ойи изследването може да се извърши само за интервала.
и критични точки на функцията:
;
,
и определете неговия знак при: получаваме . Тъй като и , това е минималната точка на функцията и 
.
,Продължаваме заедно да търсим екстремуми на функцията
Достатъчен знак за нарастваща функция.
Ако f’(x) > 0 във всяка точка от интервала I, тогава функцията f нараства с I.
Достатъчен знак за намаляваща функция.
Ако f'(x)< 0 в каждой точке интервала I, то функция f убывает на I.
Доказателството за тези признаци се извършва въз основа на формулата на Лагранж (виж параграф 19). Вземете произволни две числа x 1 и х 2 от интервала. Нека x 1
(1)
Числото c принадлежи на интервала I, тъй като точките x 1 и х 2 принадлежат на I. Ако f"(x)>0 за x∈I тогава f’(c)>0 и следователно F(x 1 )
Визуалното значение на знаците е ясно от физическите разсъждения (за категоричност нека разгледаме знака за увеличение).
Нека точка, движеща се по ординатната ос в момент t, има ордината y = f(t). Тогава скоростта на тази точка в момента t е равна на f"(t) (виж.Мигновена скорост ). Ако f’ (t)>0 във всеки момент от интервала t, тогава точката се движи в положителната посока на ординатната ос, т.е. 1
Бележка 1.
Ако функцията f е непрекъсната в който и да е край на нарастващия (намаляващия) интервал, тогава тази точка е прикрепена към този интервал.
Бележка 2.
За решаване на неравенствата f" (x)>0 и f" (x)<0 удобно пользоваться обобщением метода интервалов (теоремой Дарбу) : точки, в которых производная равна 0 или не существует, разбивают область определения функции f на промежутки, в каждом из которых f" сохраняет постоянный знак. (Этот факт доказывается в курсах математического анализа.) Знак можно определить, вычислив значение f" в какой-нибудь точке промежутка.
Необходимо условие за екстремум
Достатъчно условие за екстремум
