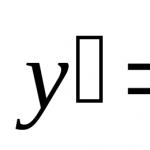Нека разгледам материална точка, чието движение е ограничено по такъв начин, че има само една степен на свобода.
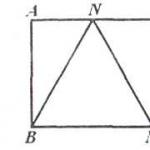
Това означава, че неговата позиция може да бъде определена с помощта на едно количество, като например координатата x. Пример за това е топка, плъзгаща се без триене по неподвижен проводник, огънат във вертикална равнина (фиг. 26.1а).
Друг пример е топка, прикрепена към края на пружина, плъзгаща се без триене към хоризонтален водач (фиг. 26.2, а).

Върху топката действа консервативна сила: в първия случай това е силата на гравитацията, във втория случай е еластичната сила на деформирана пружина. Графиките на потенциалната енергия са показани на фиг. 26.1, b и 26.2, b.
Тъй като топките се движат по телта без триене, силата, с която телта действа върху топката, и в двата случая е перпендикулярна на скоростта на топката и следователно не извършва работа върху топката. Следователно спестяването на енергия се осъществява:
От (26.1) следва, че кинетичната енергия може да се увеличи само поради намаляване на амплитудната енергия. Следователно, ако топката е в такова състояние, че нейната скорост е нула и потенциалната енергия има минимална стойност, тогава без външно въздействие тя няма да може да се движи, т.е. ще бъде в равновесие.
Минимумите на U съответстват на равни стойности в графиките (на фиг. 26.2 има дължина на недеформирания отряд) Условието за минималната потенциална енергия има формата
В съответствие с t (22.4), условие (26.2) е еквивалентно на факта, че
(в случай, когато U е функция само на една променлива, ). По този начин позицията, съответстваща на минималната потенциална енергия, има свойството, че силата, действаща върху тялото, е нула.
В случая, показан на фиг. 26.1, условията (26.2) и (26.3) също са изпълнени за x равно на (т.е. за максимума на U). Позицията на топката, определена от тази стойност, също ще бъде равновесна. Това равновесие обаче, за разлика от равновесието при , ще бъде нестабилно: достатъчно е леко да извадите топката от тази позиция и ще възникне сила, която ще отдалечи топката от позицията . Силите, които възникват, когато топката се измести от стабилно равновесно положение (за което ) са насочени по такъв начин, че се стремят да върнат топката в равновесно положение.
Познавайки вида на функцията t, която изразява потенциалната енергия, можем да направим редица заключения за естеството на движението на частицата. Нека обясним това с помощта на графиката, показана на фиг. 26.1, б. Ако общата енергия има стойността, посочена на фигурата, тогава частицата може да се движи или в диапазона от до, или в диапазона от до безкрайност. Частицата не може да проникне в областта, тъй като потенциалната енергия не може да стане по-голяма от общата енергия (ако това се случи, кинетичната енергия ще стане отрицателна). По този начин регионът представлява потенциална бариера, през която дадена частица не може да проникне при дадено количество обща енергия. Районът се нарича потенциален кладенец.
Ако една частица не може да се отдалечи до безкрайност по време на своето движение, движението се нарича крайно. Ако частицата може да достигне желаното разстояние, движението се нарича безкрайно. Една частица в потенциална яма претърпява ограничено движение. Движението на частица с отрицателна обща енергия в централното поле на привличащите сили също ще бъде ограничено (приема се, че потенциалната енергия изчезва в безкрайност).
Позволява ви да анализирате общите модели на движение, ако е известна зависимостта на потенциалната енергия от координатите. Да разгледаме например едномерното движение на материална точка (частица) по оста 0xв потенциалното поле, показано на фиг. 4.12.
Фиг.4.12. Движение на частица в близост до стабилни и нестабилни равновесни положения
Тъй като в еднообразно гравитационно поле потенциалната енергия е пропорционална на височината на издигане на тялото, може да си представим ледена пързалка (пренебрегвайки триенето) с профил, съответстващ на функцията P(x)върху изображението.
От закона за запазване на енергията E = K + Pи от факта, че кинетичната енергия K = E - Pвинаги е неотрицателна, от това следва, че частицата може да бъде само в области, където E > P. Фигурата показва частица с пълна енергия дможе да се движи само в области
В първата област движението му ще бъде ограничено (крайно): при даден запас от обща енергия частицата не може да преодолее „пързалките“ по пътя си (те се наричат потенциални бариери) и е обречен да остане завинаги в „долината“ между тях. Вечно - от гледна точка на класическата механика, която сега изучаваме. В края на курса ще видим как квантовата механика помага на частица да избяга от затвора в потенциален кладенец - регион
Във втората област движението на частицата не е ограничено (безкрайно), тя може да се движи безкрайно далеч от началото надясно, но вляво движението й все още е ограничено от потенциалната бариера:
Видео 4.6. Демонстрация на крайни и безкрайни движения.
В екстремни точки на потенциална енергия x МИНИ x МАКСсилата, действаща върху частицата, е нула, тъй като производната на потенциалната енергия е нула:
![]()
Ако поставите частица в покой в тези точки, тогава тя ще остане там... отново завинаги, ако не бяха колебанията в нейната позиция. В този свят няма нищо строго в покой; една частица може да преживее малко отклонения (флуктуации) от равновесното положение. В този случай естествено възникват сили. Ако те върнат частицата в равновесно положение, тогава се нарича такова равновесие устойчиви. Ако, когато частицата се отклони, произтичащите сили я отвеждат още по-далеч от нейното равновесно положение, тогава имаме работа с нестабиленравновесие и частицата обикновено не остава дълго в това положение. По аналогия с ледената пързалка може да се предположи, че стабилна позиция ще бъде при минимум потенциална енергия, а нестабилна при максимум.
Нека докажем, че това наистина е така. За частица в екстремна точка х М (x МИНили x МАКС) сила, действаща върху него F x (x M) = 0. Нека координатата на частицата се промени с малко поради флуктуация х. При такава промяна на координатите върху частицата ще започне да действа сила
(основното число показва производната по отношение на координатата х). Като се има предвид това F x =-P", получаваме израза за силата
В минималната точка втората производна на потенциалната енергия е положителна: U"(x MIN) > 0. След това, за положителни отклонения от равновесното положение х > 0 резултантната сила е отрицателна, а когато х<0 силата е положителна. И в двата случая силата пречи на частицата да промени своите координати и равновесното положение при минимална потенциална енергия е стабилно.
Напротив, в максималната точка втората производна е отрицателна: U"(x MAX)<0 . Тогава увеличаването на координатата на частицата Δx води до появата на положителна сила, която допълнително увеличава отклонението от равновесното положение. При х<0 силата е отрицателна, тоест в този случай допринася за по-нататъшно отклонение на частицата. Това равновесно положение е нестабилно.

По този начин позицията на стабилно равновесие може да бъде намерена чрез съвместно решаване на уравнението и неравенството
Видео 4.7. Потенциални дупки, потенциални бариери и равновесие: стабилно и нестабилно.
Пример. Потенциалната енергия на двуатомна молекула (напр. H 2или О 2) се описва чрез израз на формата
![]()
Където rе разстоянието между атомите и А, б- положителни константи. Определете равновесното разстояние r Ммежду атомите на една молекула. Стабилна ли е двуатомната молекула?
Решение. Първият термин описва отблъскването на атомите на къси разстояния (молекулата се съпротивлява на компресия), вторият описва привличането на големи разстояния (молекулата се съпротивлява на счупване). В съответствие с казаното равновесното разстояние се намира чрез решаване на уравнението
Диференцирайки потенциалната енергия, получаваме
![]()

Сега намираме втората производна на потенциалната енергия
![]()
и заместете стойността на равновесното разстояние там r М :

Равновесното положение е стабилно.
На фиг. 4.13 е представен експеримент за изследване на потенциални криви и условия на равновесие на топка. Ако върху модела на потенциалната крива топка е поставена на височина, по-голяма от височината на потенциалната бариера (енергията на топката е по-голяма от енергията на бариерата), тогава топката преодолява потенциалната бариера. Ако началната височина на топката е по-малка от височината на преградата, тогава топката остава в потенциалната яма.
Топка, поставена в най-високата точка на потенциалната бариера, е в нестабилно равновесие, тъй като всяко външно влияние води до преместване на топката в най-ниската точка на потенциалната яма. В долната точка на потенциалната яма топката е в стабилно равновесие, тъй като всяко външно влияние води до връщане на топката в долната точка на потенциалната яма.

Ориз. 4.13. Експериментално изследване на потенциални криви
Допълнителна информация
http://vivovoco.rsl.ru/quantum/2001.01/KALEID.PDF – Приложение към списание „Квант” – дискусии за стабилно и нестабилно равновесие (А. Леонович);
http://mehanika.3dn.ru/load/24-1-0-3278 – Тарг С.М. Кратък курс по теоретична механика, Издателство на ВУЗ, 1986 г. – стр. 11–15, §2 – начални положения на статиката.
Механичен баланс
Механичен баланс- състояние на механична система, при което сумата от всички сили, действащи върху всяка от нейните частици, е равна на нула и сумата от моментите на всички сили, приложени към тялото спрямо всяка произволна ос на въртене, също е нула.
В състояние на равновесие тялото е в покой (векторът на скоростта е нула) в избраната отправна система, или се движи равномерно по права линия, или се върти без тангенциално ускорение.
Определение чрез системна енергия
Тъй като енергията и силите са свързани с фундаментални взаимоотношения, това определение е еквивалентно на първото. Въпреки това, определението по отношение на енергията може да бъде разширено, за да предостави информация за стабилността на равновесното положение.
Видове баланс
Да дадем пример за система с една степен на свобода. В този случай достатъчно условие за равновесното положение ще бъде наличието на локален екстремум в изследваната точка. Както е известно, условието за локален екстремум на диференцируема функция е нейната първа производна да е равна на нула. За да определите кога тази точка е минимум или максимум, трябва да анализирате нейната втора производна. Стабилността на равновесното положение се характеризира със следните опции:
- нестабилно равновесие;
- стабилен баланс;
- безразлично равновесие.
Нестабилно равновесие
В случай, че втората производна е отрицателна, потенциалната енергия на системата е в състояние на локален максимум. Това означава, че равновесното положение нестабилен. Ако системата се измести на малко разстояние, тя ще продължи движението си поради силите, действащи върху системата.
Стабилен баланс
Втора производна > 0: потенциална енергия при локален минимум, равновесно положение устойчиви(вижте теоремата на Лагранж за стабилността на равновесието). Ако системата се измести на малко разстояние, тя ще се върне обратно в своето равновесно състояние. Равновесието е стабилно, ако центърът на тежестта на тялото заема най-ниската позиция в сравнение с всички възможни съседни позиции.
Безразлично равновесие
Втора производна = 0: в тази област енергията не се променя и равновесното положение е безразличен. Ако системата се премести на малко разстояние, тя ще остане в новата позиция.
Устойчивост в системи с голям брой степени на свобода
Ако една система има няколко степени на свобода, тогава може да се окаже, че при промени в едни посоки равновесието е стабилно, но в други е нестабилно. Най-простият пример за такава ситуация е „седло“ или „проход“ (би било добре да поставите снимка на това място).
Равновесието на система с няколко степени на свобода ще бъде стабилно само ако е стабилно във всички посоки.
Фондация Уикимедия. 2010 г.
Вижте какво е „механичен баланс“ в други речници:
механичен баланс- mechaninė pusiausvyra statusas T sritis fizika atitikmenys: англ. механично равновесие vok. mechanisches Gleichgewicht, n рус. механично равновесие, n pranc. équilibre mécanique, m … Fizikos terminų žodynas
- ... Уикипедия
Фазови преходи Член I ... Wikipedia
Състоянието на термодинамична система, до което тя идва спонтанно след достатъчно дълъг период от време при условия на изолация от околната среда, след което параметрите на състоянието на системата вече не се променят във времето. Изолация... ... Велика съветска енциклопедия
РАВНОВЕСИЕ- (1) механичното състояние на неподвижност на тялото, което е следствие от действащите върху него R. сили (когато сумата от всички сили, действащи върху тялото, е равна на нула, т.е. не придава ускорение) . Р. се отличават: а) стабилни, когато при отклонение от ... ... Голяма политехническа енциклопедия
Механично състояние система, в която всички нейни точки са неподвижни спрямо дадената отправна система. Ако тази отправна система е инерциална, тогава се нарича R.M. абсолютно, иначе относително. В зависимост от поведението на тялото след... Голям енциклопедичен политехнически речник
Термодинамичното равновесие е състояние на изолирана термодинамична система, при която във всяка точка за всички химични, дифузионни, ядрени и други процеси скоростта на правата реакция е равна на скоростта на обратната. Термодинамични... ... Уикипедия
Равновесие- най-вероятното макросъстояние на веществото, когато променливите, независимо от избора, остават постоянни с пълно описание на системата. Равновесието се различава: механично, термодинамично, химично, фазово и др.: Вижте... ... Енциклопедичен речник по металургия
Съдържание 1 Класическа дефиниция 2 Дефиниция чрез енергията на системата 3 Видове равновесие ... Wikipedia
Фазови преходи Статията е част от поредицата Термодинамика. Концепция за фаза Фазово равновесие Квантов фазов преход Раздели на термодинамиката Принципи на термодинамиката Уравнение на състоянието ... Wikipedia
Известно е, че за равновесието на система с идеални връзки е необходимо и достатъчно или. (7)
Тъй като вариациите на обобщените координати са независими една от друга и като цяло не са равни на нула, е необходимо  ,
, ,…,
,…, .
.
За равновесието на система с холономни задържащи, стационарни, идеални ограничения е необходимо и достатъчно всички обобщени сили, съответстващи на избраните обобщени координати, да бъдат равни на нула.
Случай на потенциални сили:
Ако системата е в потенциално силово поле, тогава
 ,
,
 ,…,
,…,
 ,
,
 ,…,
,…,
Тоест, равновесните позиции на системата могат да бъдат само за тези стойности на обобщени координати, за които функцията на силата Uи потенциална енергия Пимат екстремни стойности ( максили мин).
Концепцията за устойчивост на равновесие.
След като се определят позициите, в които системата може да бъде в равновесие, е възможно да се определи кои от тези позиции са реализируеми и кои са нереализируеми, тоест да се определи коя позиция е стабилна и коя е нестабилна.

Като цяло, необходимо знак за устойчивост на равновесие според Ляпунов може да се формулира по следния начин:
Нека премахнем системата от равновесно положение, като предоставим малки стойности на модула на обобщените координати и техните скорости. Ако при по-нататъшно разглеждане на системата обобщените координати и техните скорости остават малки по величина, т.е. системата не се отклонява далеч от равновесното положение, тогава такова равновесно положение е стабилно.
Достатъчно условие за устойчивост на равновесие система е определена Теорема на Лагранж-Дирихле :
Ако в равновесно положение на механична система с идеални връзки потенциалната енергия има минимална стойност, то такова равновесно положение е стабилно.


 ,
,
 - устойчиви.
- устойчиви.
Равновесието на механична система е състояние, при което всички точки на разглежданата система са в покой спрямо избраната отправна система.
Най-лесният начин да разберете условията на равновесие е чрез примера на най-простата механична система - материална точка. Според първия закон на динамиката (виж Механика) условието за покой (или равномерно линейно движение) на материална точка в инерционна координатна система е векторната сума на всички приложени към нея сили да е равна на нула.
При преминаване към по-сложни механични системи само това условие не е достатъчно за тяхното равновесие. В допълнение към транслационното движение, което се причинява от некомпенсирани външни сили, сложна механична система може да претърпи въртеливо движение или деформация. Нека да открием условията на равновесие за абсолютно твърдо тяло - механична система, състояща се от съвкупност от частици, взаимните разстояния между които не се променят.
Възможността за постъпателно движение (с ускорение) на механична система може да бъде елиминирана по същия начин, както в случая на материална точка, като се изисква сумата от силите, приложени към всички точки на системата, да бъде равна на нула. Това е първото условие за равновесие на една механична система.
В нашия случай твърдото тяло не може да се деформира, тъй като сме се съгласили, че взаимните разстояния между точките му не се променят. Но за разлика от материалната точка, двойка равни и противоположно насочени сили могат да бъдат приложени към абсолютно твърдо тяло в различни точки. Освен това, тъй като сумата на тези две сили е нула, разглежданата механична система няма да извършва постъпателно движение. Очевидно е обаче, че под въздействието на такава двойка сили тялото ще започне да се върти спрямо определена ос с все по-голяма ъглова скорост.
Появата на въртеливо движение в разглежданата система се дължи на наличието на некомпенсирани моменти на сили. Моментът на сила около която и да е ос е произведението на големината на тази сила F от рамото d, т.е. от дължината на перпендикуляра, спуснат от точка O (виж фигурата), през която минава оста, и от посоката на силата. Имайте предвид, че моментът на сила с тази дефиниция е алгебрична величина: счита се за положителен, ако силата води до въртене обратно на часовниковата стрелка, и за отрицателен в противен случай. По този начин второто условие за равновесие на твърдо тяло е изискването сумата от моментите на всички сили спрямо всяка ос на въртене да бъде равна на нула.
В случай, че са изпълнени и двете намерени условия за равновесие, твърдото тяло ще бъде в покой, ако в момента, в който силите са започнали да действат, скоростите на всички негови точки са били равни на нула.
В противен случай той ще извършва равномерно движение по инерция.
Разгледаната дефиниция на равновесие на механична система не казва нищо за това какво ще се случи, ако системата леко се измести от равновесното си положение. В този случай има три възможности: системата ще се върне към предишното си състояние на равновесие; системата, въпреки отклонението, няма да промени равновесното си състояние; системата ще излезе от равновесие. Първият случай се нарича стабилно състояние на равновесие, вторият - безразлично, третият - нестабилно. Характерът на равновесното положение се определя от зависимостта на потенциалната енергия на системата от координатите. Фигурата показва всичките три вида равновесие, използвайки примера на тежка топка, разположена в депресия (стабилно равновесие), върху гладка хоризонтална маса (безразлично), на върха на туберкул (нестабилно) (вижте фигурата на стр. 220) .
Горният подход към проблема за равновесието на механична система е бил разглеждан от учените още в древния свят. Така законът за равновесието на лоста (т.е. твърдо тяло с фиксирана ос на въртене) е открит от Архимед през 3 век. пр.н.е д.
През 1717 г. Йохан Бернули разработва напълно различен подход за намиране на условията на равновесие на механична система - методът на виртуалните премествания. Тя се основава на свойството на силите на реакция на връзката, произтичащи от закона за запазване на енергията: при малко отклонение на системата от равновесното положение общата работа на силите на реакция на връзката е нула.
При решаване на проблеми на статиката (виж Механика) въз основа на условията на равновесие, описани по-горе, връзките, съществуващи в системата (опори, резби, пръти), се характеризират с възникващите в тях сили на реакция. Необходимостта да се вземат предвид тези сили при определяне на условията на равновесие в случай на системи, състоящи се от няколко тела, води до тромави изчисления. Въпреки това, поради факта, че работата на силите на реакция на връзката е равна на нула при малки отклонения от равновесното положение, е възможно да се избегне изобщо отчитането на тези сили.
В допълнение към силите на реакция, външни сили също действат върху точки на механична система. Каква е тяхната работа при малко отклонение от равновесното положение? Тъй като системата първоначално е в покой, за всяко движение е необходимо да се извърши някаква положителна работа. По принцип тази работа може да се извърши както от външни сили, така и от сили на реакция на връзка. Но, както вече знаем, общата работа, извършена от силите за реакция, е нула. Следователно, за да може системата да излезе от състоянието на равновесие, общата работа на външните сили за всяко възможно изместване трябва да бъде положителна. Следователно условието за невъзможност за движение, т.е. условието за равновесие, може да се формулира като изискването общата работа на външните сили да бъде неположителна за всяко възможно движение: .
Да приемем, че когато точките на системата се движат, сумата от работата, извършена от външни сили, се оказва равна на . И какво се случва, ако системата прави движения - Тези движения са възможни по същия начин като първите; но работата на външните сили сега ще промени знака: . Разсъждавайки подобно на предишния случай, ще стигнем до извода, че сега състоянието на равновесие на системата има формата: , т.е. работата на външните сили трябва да е неотрицателна. Единственият начин да се „помирят” тези две почти противоречиви условия е да се изисква точно равенство на нула на общата работа на външните сили за всяко възможно (виртуално) изместване на системата от равновесно положение: . Под възможно (виртуално) движение тук разбираме безкрайно малко мисловно движение на системата, което не противоречи на наложените й връзки.
И така, условието за равновесие на механична система под формата на принципа на виртуалните премествания се формулира, както следва:
„За равновесието на всяка механична система с идеални връзки е необходимо и достатъчно сумата от елементарните работи на силите, действащи върху системата за всяко възможно изместване, да е равна на нула.“
Използвайки принципа на виртуалните премествания, се решават проблеми не само на статиката, но и на хидростатиката и електростатиката.