Другата страна на равенството е неравенство. В тази статия ще въведем понятието неравенства и ще дадем основна информация за тях в контекста на математиката.
Първо, нека да разгледаме какво е неравенство и да въведем понятията не е равно, по-голямо от, по-малко. След това ще говорим за записване на неравенства с помощта на знаците не е равно, по-малко от, по-голямо от, по-малко от или равно на, по-голямо от или равно на. След това ще се докоснем до основните видове неравенства, ще дадем дефиниции на строги и нестроги, верни и грешни неравенства. След това нека накратко изброим основните свойства на неравенствата. И накрая, нека да разгледаме двойките, тройките и т.н. неравенства и нека да разгледаме значението, което носят.
Навигация в страницата.
Какво е неравенство?
Понятие за неравенство, подобно на , се свързва със сравнението на два обекта. И ако равенството се характеризира с думата „идентичен“, тогава неравенството, напротив, говори за разликата между сравняваните обекти. Например обектите и са еднакви, за тях можем да кажем, че са равни. Но двата обекта са различни, т.е не е равноили неравен.
Неравенството на сравняваните обекти се разпознава заедно със значението на думи като по-висок, по-нисък (неравенство във височина), по-дебел, по-тънък (неравенство в дебелина), по-нататък, по-близо (неравенство в разстоянието от нещо), по-дълъг, по-къс (неравенство в дължина), по-тежък, по-лек (неравенство на теглото), по-ярък, по-слаб (неравенство на яркостта), по-топъл, по-студен и т.н.
Както вече отбелязахме при запознаването с равенствата, можем да говорим както за равенство на два обекта като цяло, така и за равенство на някои техни характеристики. Същото важи и за неравенствата. Като пример даваме два обекта и . Очевидно те не са еднакви, тоест като цяло са неравностойни. Нито са равни по размер, нито са равни по цвят, но можем да говорим за еднаквост на формите им - и двете са кръгове.
В математиката общото значение на неравенството остава същото. Но в своя контекст ние говорим заза неравенството на математически обекти: числа, стойности на изрази, стойности на всякакви величини (дължини, тегла, площи, температури и т.н.), фигури, вектори и др.
Не равно, по-голямо, по-малко
Понякога ценността е самият факт, че два обекта са неравни. И когато се сравняват стойностите на каквито и да е количества, след като открият неравенството им, те обикновено отиват по-далеч и откриват какво количество Повече ▼, а коя – по-малко.
Научаваме значението на думите „повече” и „по-малко” почти от първите дни на живота си. На интуитивно ниво възприемаме концепцията за повече и по-малко по отношение на размер, количество и т.н. И тогава постепенно започваме да осъзнаваме за какво всъщност говорим сравнение на числата, съответстващи на броя на определени обекти или стойностите на определени количества. Тоест в тези случаи откриваме кое число е по-голямо и кое по-малко.
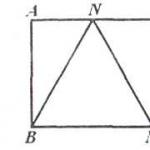
Да дадем пример. Да разгледаме две отсечки AB и CD и да сравним дължините им  . Очевидно те не са равни и също така е очевидно, че отсечката AB е по-дълга от отсечката CD. Така, според значението на думата „по-дълъг“, дължината на сегмента AB е по-голяма от дължината на сегмента CD и в същото време дължината на сегмента CD е по-малка от дължината на сегмента AB.
. Очевидно те не са равни и също така е очевидно, че отсечката AB е по-дълга от отсечката CD. Така, според значението на думата „по-дълъг“, дължината на сегмента AB е по-голяма от дължината на сегмента CD и в същото време дължината на сегмента CD е по-малка от дължината на сегмента AB.
Друг пример. Сутринта температурата на въздуха беше 11 градуса по Целзий, а следобед – 24 градуса. Според 11 е по-малко от 24, следователно стойността на температурата сутрин е била по-малка от стойността й на обяд (температурата на обяд стана по-висока от температурата сутрин).
Записване на неравенства със знаци
Буквата има няколко символа за запис на неравенства. Първият е не знак за равенство, представлява зачеркнат знак за равенство: ≠. Знакът за неравенство се поставя между неравни обекти. Например записът |AB|≠|CD| означава, че дължината на отсечката AB не е равна на дължината на отсечката CD. По същия начин 3≠5 – три не е равно на пет.
Знакът за по-голямо от > и знакът за по-малко от ≤ се използват по подобен начин. Между по-големи и по-малки обекти се записва знакът за по-голямо, а между по-малки и по-големи обекти - знакът за по-малко. Нека дадем примери за използването на тези знаци. Записът 7>1 се чете като седем върху едно и можете да напишете, че площта на триъгълник ABC е по-малка от площта на триъгълник DEF, като използвате знака ≤ като SABC≤SDEF.
Също така широко се използва знакът по-голямо или равно на формата ≥, както и знакът по-малко или равно на ≤. Ще говорим повече за тяхното значение и цел в следващия параграф.
Нека също да отбележим, че алгебричните обозначения със знаци неравно, по-малко, по-голямо, по-малко или равно, по-голямо или равно, подобни на тези, разгледани по-горе, се наричат неравенства. Освен това има дефиниция на неравенствата в смисъла на начина, по който са написани:
Определение.
Неравенства- това са смислени алгебрични изрази, съставен с помощта на знаци ≠,<, >, ≤, ≥.
Строги и нестроги неравенства
Определение.
Знаците се наричат по-малко знаци строги неравенства , а записаните с тяхна помощ неравенства са строги неравенства.
На свой ред
Определение.
Наричат се знаците по-малко или равно на ≤ и по-голямо или равно на ≥ признаци на слаби неравенства, а неравенствата, компилирани с тях, са нестроги неравенства.
Обхватът на приложение на строгите неравенства е ясен от информацията по-горе. Защо са необходими слаби неравенства? На практика с тяхна помощ е удобно да се моделират ситуации, които могат да бъдат описани с фразите „не повече“ и „не по-малко“. Фразата „не повече“ по същество означава по-малко или същото; отговаря се със знак за по-малко от или равен на формата ≤. По същия начин „не по-малко“ означава същото или повече и е свързано със знака за по-голямо или равно ≥.
От тук става ясно защо знаците< и >се наричат признаци на строги неравенства, а ≤ и ≥ – нестроги. Първите изключват възможността за равенство на обектите, а вторите я допускат.
За да завършим този раздел, ще покажем няколко примера за използване на нестроги неравенства. Например, като използвате знака за по-голямо или равно, можете да запишете факта, че a е неотрицателно число като |a|≥0. Друг пример: известно е, че средното геометрично на две положителни числа a и b са по-малки или равни на тяхната средна аритметична стойност, т.е. ![]() .
.
Верни и грешни неравенства
Неравенствата могат да бъдат верни или неверни.
Определение.
Неравенството е верен, ако отговаря на смисъла на въведеното по-горе неравенство, в противен случай е така неверен.
Нека дадем примери за верни и грешни неравенства. Например 3≠3 е неправилно неравенство, тъй като числата 3 и 3 са равни. Друг пример: нека S е площта на някаква фигура, тогава S<−7 – неверное неравенство, так как известно, что площадь фигуры по определению выражается неотрицательным числом. И еще пример неверного неравенства: |AB|>|AB| . Но неравенствата са −3<12 , |AB|≤|AC|+|BC| и |−4|≥0 – верные. Первое из них отвечает , второе – выражает неравенство на триъгълник, а третият е в съответствие с дефиницията на модула на число.
Обърнете внимание, че заедно с фразата „истинско неравенство“ се използват следните фрази: „справедливо неравенство“, „има неравенство“ и т.н., което означава едно и също нещо.
Свойства на неравенствата
Според начина, по който въведохме понятието неравенство, можем да опишем основното свойства на неравенствата. Ясно е, че обектът не може да бъде равен на себе си. Това е първото свойство на неравенствата. Второто свойство е не по-малко очевидно: ако първият обект не е равен на втория, то вторият не е равен на първия.
Понятията „по-малко“ и „повече“, въведени на определено множество, определят така наречените отношения „по-малко“ и „повече“ на оригиналното множество. Същото важи и за отношенията „по-малко или равно на“ и „по-голямо или равно на“. Те също имат характерни свойства.
Да започнем със свойствата на отношенията, на които съответстват знаците< и >. Нека ги изброим, след което ще дадем необходимите коментари за пояснение:
- антирефлексивност;
- антисиметрия;
- преходност.
Свойството антирефлексивност може да бъде написано с помощта на букви, както следва: за всеки обект a неравенствата a>a и a b , след това b а. И накрая, свойството на транзитивност е това от a b и b>c следва, че a>c . Това свойство също се възприема съвсем естествено: ако първият обект е по-малък (по-голям) от втория, а вторият е по-малък (по-голям) от третия, тогава е ясно, че първият обект е дори по-малък (по-голям) от третия .
От своя страна отношенията „по-малко или равно на“ и „по-голямо или равно на“ имат следните свойства:
- рефлексивност: важат неравенствата a≤a и a≥a (тъй като включват случая a=a);
- антисиметрия: ако a≤b, тогава b≥a, и ако a≥b, тогава b≤a;
- транзитивност: от a≤b и b≤c следва, че a≤c, а от a≥b и b≥c следва, че a≥c.
Двойни, тройни неравенства и др.
Свойството на транзитивност, което засегнахме в предишния параграф, ни позволява да съставим така наречените двойни, тройни и т.н. неравенства, които са вериги от неравенства. Като пример нека дадем двойното неравенство a Сега нека да разгледаме как да разбираме такива записи. Те трябва да се тълкуват в съответствие със значението на знаците, които съдържат. Например двойно неравенство a В заключение отбелязваме, че понякога е удобно да се използват обозначения под формата на вериги, съдържащи както равни, така и неравни знаци, както и строги и нестроги неравенства. Например x=2 Библиография. „Равенството“ е тема, която учениците се изучават още в началното училище. Това също върви ръка за ръка с „Неравенствата“. Тези две понятия са тясно свързани помежду си. Освен това те са свързани с термини като уравнения и идентичности. И така, какво е равенството? Този термин се отнася до твърдения, които съдържат знака „=“. Равенствата се делят на верни и неверни. Ако в записа вместо = има<, >, тогава говорим за неравенства. Между другото, първият знак за равенство показва, че и двете части на израза са идентични по своя резултат или запис. В допълнение към концепцията за равенство, училището изучава и темата „Числено равенство“. Това твърдение се отнася до два числови израза, които стоят от двете страни на знака =. Например 2*5+7=17. И двете части на записа са равни една на друга. Числовите изрази от този тип могат да използват скоби, които влияят на реда на операциите. И така, има 4 правила, които трябва да се вземат предвид при изчисляване на резултатите от числови изрази. И така, сега е ясно какво е равенство. В бъдеще ще бъдат разгледани концепциите за уравнения, идентичности и методи за тяхното изчисляване. Какво е равенство? Изучаването на тази концепция изисква познаване на свойствата на числовите идентичности. Текстовите формули по-долу ви позволяват да проучите по-добре тази тема. Разбира се, тези свойства са по-подходящи за изучаване на математика в гимназията. 1. Числовото равенство няма да бъде нарушено, ако към двете части на съществуващия израз се добави едно и също число. А = Б↔ A + 5 = B + 5 2. Уравнението няма да бъде нарушено, ако двете му части се умножат или разделят на едно и също число или израз, който е различен от нула. P = O↔ P ∙ 5 = O ∙ 5 P = O↔ P: 5 = O: 5 3. Като добавим към двете страни на идентичността една и съща функция, която има смисъл за всякакви допустими стойности на променливата, получаваме ново равенство, което е еквивалентно на първоначалното. F(X) = Ψ(Х) ↔ F(X) + R(X) =Ψ
(X) + R(X) 4. Всеки термин или израз може да бъде преместен от другата страна на знака за равенство, но знаците трябва да бъдат обърнати. X + 5 = Y - 20 ↔ X = Y - 20 - 5 ↔ X = Y - 25 5. Като умножим или разделим двете страни на уравнението с една и съща функция, която е различна от нула и има значение за всяка стойност на X от ODZ, получаваме ново уравнение, което е еквивалентно на първоначалното. F(X) = Ψ(Х)↔
F(X)∙R(X) = Ψ(X)∙R(Х) F(X) = Ψ(Х)↔
F(X) : G(X) = Ψ(X) : G(X) Горните правила ясно показват принципа на равенство, който съществува при определени условия. В математиката има такова нещо като равенство на отношенията. В този случай се подразбира определението за пропорция. Ако разделите A на B, резултатът ще бъде отношението на числото A към числото B. Пропорцията е равенство на две съотношения: Понякога пропорцията се записва, както следва: A:B=° С:Д.Това предполага основното свойство на пропорцията: А*D=Д*° С, където A и D са екстремните членове на пропорцията, а B и C са средните. Идентичността е равенство, което ще бъде вярно за всички допустими стойности на променливите, включени в задачата. Идентичностите могат да бъдат представени като буквални или числови равенства. Изрази, които съдържат неизвестна променлива от двете страни на равенството, което може да приравни две части от едно цяло, се наричат идентично равни. Ако замените един израз с друг, който ще бъде равен на него, тогава говорим за идентична трансформация. В този случай можете да използвате формули за съкратено умножение, законите на аритметиката и други идентичности. За да намалите дроб, трябва да извършите идентични трансформации. Например дадена дроб. За да получите резултата, трябва да използвате формули за съкратено умножение, факторизиране, опростяване на изрази и намаляване на дроби. Струва си да се има предвид, че този израз ще бъде идентичен, когато знаменателят не е равен на 3. За да докажете равенството на идентичността, трябва да трансформирате изразите. Метод I Необходимо е да се извършат еквивалентни трансформации от лявата страна. Резултатът е дясната страна и можем да кажем, че идентичността е доказана. II метод Всички действия за трансформиране на изрази се извършват от дясната страна. Резултатът от извършените манипулации е лявата страна. Ако и двете части са идентични, тогава идентичността е доказана. III метод „Трансформации“ се случват и в двете части на израза. Ако резултатът е две еднакви части, идентичността се доказва. IV метод Дясната страна се изважда от лявата страна. В резултат на еквивалентни трансформации резултатът трябва да бъде нула. Тогава можем да говорим за идентичност на израза. V метод Лявата страна се изважда от дясната страна. Всички еквивалентни трансформации се свеждат до гарантиране, че отговорът съдържа нула. Само в този случай можем да говорим за идентичност на равенството. В математиката свойствата на равенствата често се използват за ускоряване на процеса на изчисление. Благодарение на основните алгебрични идентичности, процесът на изчисляване на някои изрази ще отнеме броени минути вместо дълги часове. По своята същност формулите за съкратено умножение са равенства. Те помагат за решаването на много задачи по математика поради тяхната простота и лекота на използване. Съкратените формули за умножение често се използват, ако е необходимо да се доведе полином до обичайната му форма, опростявайки го по всички възможни начини. Представените формули са лесни за доказване: просто отворете скобите и добавете подобни членове. След като проучите въпроса какво е равенството, можете да преминете към следващата точка: Уравнението се разбира като равенство, в което присъстват неизвестни количества. Решаването на уравнение е намирането на всички стойности на променлива, така че двете страни на целия израз да са равни. Има и задачи, в които намирането на решения на уравнение е невъзможно. В този случай казват, че няма корени. По правило равенствата с неизвестни произвеждат цели числа като решения. Възможно е обаче да има случаи, когато коренът е вектор, функция или други обекти. Уравнението е едно от най-важните понятия в математиката. Повечето научни и практически проблеми не позволяват да се измери или изчисли каквото и да е количество. Следователно е необходимо да се създаде съотношение, което да отговаря на всички условия на задачата. В процеса на съставяне на такава връзка се появява уравнение или система от уравнения. Обикновено решаването на равенство с неизвестно се свежда до трансформиране на сложно уравнение и редуцирането му до прости форми. Трябва да се помни, че трансформациите трябва да се извършват от двете страни, в противен случай изходът ще бъде неправилен. Под решаване на уравнение разбираме замяна на дадено равенство с друго, което е еквивалентно на първото. Такова заместване е известно като трансформация на идентичността. За да решите уравнението, трябва да използвате един от методите. 1. Един израз се заменя с друг, който задължително ще бъде идентичен с първия. Пример: (3∙x+3) 2 =15∙x+10. Този израз може да се преобразува в 9∙x 2 +18∙x+9=15∙x+10. 2. Прехвърляне на условия за равенство с неизвестното от едната страна към другата. В този случай е необходимо да смените знаците правилно. Най-малката грешка ще развали цялата свършена работа. Нека вземем предишната „проба“ като пример. 9∙x 2 + 12∙x + 4 = 15∙x + 10 9∙x 2 + 12∙x + 4 - 15∙x - 10 = 0 3. Умножаване на двете страни на равенство с еднакво число или израз, който не е равен на 0. Въпреки това си струва да запомните, че ако новото уравнение не е еквивалентно на равенството преди трансформациите, тогава броят на корените може да се промени значително. 4. Повдигане на квадрат на двете страни на уравнението. Този метод е просто прекрасен, особено когато има ирационални изрази в равенството, тоест изразът под него. Тук има един нюанс: ако повишите уравнението до равномерна степен, тогава могат да се появят външни корени, които ще изкривят същността на задачата. И ако извлечете корена неправилно, тогава смисълът на въпроса в проблема ще бъде неясен. Пример: │7∙х│=35 → 1) 7∙х = 35 и 2) - 7∙х = 35 → уравнението ще бъде решено правилно. И така, в тази статия се споменават термини като уравнения и идентичности. Всички те идват от концепцията за „равенство“. Благодарение на различни видове еквивалентни изрази, решаването на някои задачи е значително улеснено. В този урок вие и жабата ще се запознаете с математическите понятия: „равенство“ и „неравенство“, както и със знаци за сравнение. Със забавни и интересни примери се научете да сравнявате групи от фигури с помощта на сдвояване и сравнявайте числа с помощта на числовата ос. Предмет:Въведение в основните понятия в математиката Урок: Равенство и неравенство В този урок ще представим математически понятия: "равенство"И "неравенство". Опитайте да отговорите на въпроса: Има вани до стената, Всяка съдържа точно една жаба. Ако имаше пет вани, Колко жаби ще има в тях? (Фиг. 1) Ориз. 1 В стихотворението се казва, че имало 5 вани, всяка вана съдържала по 1 жаба, нито една не останала без двойка, което означава, че броят на жабите е равен на броя на ваните. Да означим ваните с буквата К, а жабите с буквата Л. Да напишем равенството: K = L. (фиг. 2) Ориз. 2 Сравнете броя на две групи фигури. Има много фигури, те са с различни размери, подредени без ред. (фиг. 3) Ориз. 3 Нека направим двойки от тези фигури. Нека свържем всеки квадрат с триъгълник. (фиг. 4) Ориз. 4 Два квадрата останаха без чифт. Това означава, че броят на квадратите не е равен на броя на триъгълниците. Нека означим квадратите с буквата К, а триъгълниците с буквата Т. Нека запишем неравенството: K ≠ T. (фиг. 5) Ориз. 5 Заключение: Можете да сравните броя на елементите в две групи, като направите двойки. Ако всички елементи имат достатъчно двойки, тогава съответните числа равен, в този случай го поставяме между цифри или букви =. Този запис се нарича равенство. (фиг. 6) Ориз. 6 Ако няма достатъчно двойки, т.е. има останали допълнителни елементи, тогава тези числа не е равно. Поставете между цифри или букви знак за неравенство. Този запис се нарича неравенство.(фиг. 7) Ориз. 7 Елементите, останали без двойка, показват кое от двете числа е по-голямо и с колко. (фиг. 8) Ориз. 8 Методът за сравняване на групи от фигури чрез сдвояване не винаги е удобен и отнема много време. Можете да сравнявате числа с помощта на цифров лъч. (фиг. 9) Ориз. 9 Сравнете тези числа с помощта на числова линия и поставете знак за сравнение. Трябва да сравним числата 2 и 5. Нека погледнем числовия лъч. Числото 2 е по-близо до 0 от числото 5 или казват, че числото 2 на числовата ос е по-вляво от числото 5. Това означава, че 2 не е равно на 5. Това е неравенство. Знакът “≠” (не е равен) само фиксира неравенството на числата, но не показва кое от тях е по-голямо и кое е по-малко. От двете числа на числовата ос по-малкото се намира отляво, а по-голямото отдясно. (фиг. 10) Ориз. 10 Това неравенство може да се напише по различен начин, като се използва по-малко знак "< »
или по-голям от знака ">" : На числовата ос числото 7 е по-вдясно от числото 4, следователно: 7 ≠ 4 и 7 > 4 Числата 9 и 9 са равни, затова поставяме знака =, това е равенство: Сравнете броя на точките и числото и поставете съответния знак. (фиг. 11) Ориз. единадесет На първата снимка трябва да поставим знака = или ≠. Сравнете две точки и числото 2, поставете знак = между тях. Това е равенството. Сравняваме една точка и числото 3, на числовата ос числото 1 е вляво от числото 3, поставяме знака ≠. Сравняваме четири точки и 4. Поставяме знак = между тях. Това е равенството. Сравняваме трите точки и числото 4. Трите точки са числото 3. На числовата права е вляво, поставяме знака ≠. Това е неравенство. (фиг. 12) Ориз. 12 Във втората фигура трябва да поставите знаци = между точките и числата,<, >. Нека сравним пет точки и числото 5. Поставяме знак = между тях. Това е равенството. Нека сравним трите точки и числото 3. Тук можете да поставите и знака =. Нека сравним пет точки и числото 6. На числовата ос числото 5 е вляво от числото 6. Поставяме знак<. Это неравенство. Нека сравним две точки и една, числото 2 е по-надясно на числовата ос от числото 1. Поставяме знака >. Това е неравенство. (фиг. 13) Ориз. 13 Въведете число в полето, за да направите полученото равенство и неравенство вярно. Това е неравенство. Нека погледнем числовата ос. Тъй като търсим число, по-малко от числото 7, то трябва да е отляво на числото 7 на числовата ос. (фиг. 14) Ориз. 14 Можете да вмъкнете няколко числа в прозореца. Тук са подходящи числата 0, 1, 2, 3, 4, 5, 6. Всяко от тях може да бъде заменено в прозореца и ще получите няколко верни неравенства. Например 5< 7 или 2 < 7 На числовата ос ще намерим числа, които ще бъдат по-малки от 5. (фиг. 15) Ориз. 15 Тези числа са 4, 3, 2, 1, 0. Следователно всяко от тези числа може да бъде заменено в прозореца, ще получим няколко верни неравенства. Например 5 >4, 5 >3 Може да се замени само едно число 8. В този урок се запознахме с математическите понятия: „равенство“ и „неравенство“, научихме се как правилно да поставяме знаци за сравнение, практикувахме сравняване на групи от фигури с помощта на сдвояване и сравняване на числа с помощта на числова линия, което ще помогне в по-нататъшното изучаване на математиката. Библиография Домашна работа 1. Какви знаци за сравнение знаете, в какви случаи се използват? Запишете знаците за сравнение на числата. 2. Сравнете броя на обектите на снимката и поставете знак „<», «>" или "=". 3. Сравнете числата, като поставите знака „<», «>" или "=". 1. Концепцията за равенство и неравенство 2. Свойства на равенства и неравенства. Примери за решаване на равенства и неравенства Числени равенства и неравенства Позволявам fИ ж- два числови израза. Нека ги свържем със знак за равенство. Ще получим оферта f= жкоето се нарича числово равенство. Вземете например числовите изрази 3 + 2 и 6 - 1 и ги свържете със знака за равенство 3 + 2 = 6-1. Вярно е. Ако свържем знака за равенство 3 + 2 и 7 - 3, получаваме фалшивото числово равенство 3 + 2 = 7-3. По този начин, от логическа гледна точка, численото равенство е твърдение, вярно или невярно. Численото равенство е вярно, ако стойностите на числовите изрази от лявата и дясната страна на равенството съвпадат. Свойства на равенства и неравенства Нека си припомним някои свойства на истинските числени равенства. 1.
Ако добавим един и същ числов израз, който има смисъл към двете страни на истинско числово равенство, ние също получаваме истинско числово равенство. 2.
Ако и двете страни на едно истинско числово равенство се умножат по един и същи числов израз, който има смисъл, тогава също получаваме истинско числово равенство. Позволявам fИ ж- два числови израза. Нека ги свържем със знака ">" (или "<»). Получим предложение f > ж(или f < g),което се нарича числено неравенство. Например, ако свържем израза 6 + 2 и 13-7 със знака “>”, получаваме истинското числово неравенство 6 + 2 > 13-7. Ако свържем същите изрази със знака „<», получим ложное числовое неравенство 6 + 2 < 13-7. Таким образом, с логической точки зрения числовое неравенство - это высказывание, истинное или ложное. Числените неравенства имат редица свойства. Нека разгледаме някои. 1.
Ако добавим един и същ числов израз, който има смисъл към двете страни на истинско числово неравенство, ние също получаваме истинско числово неравенство. 2.
Ако двете страни на едно истинско числово неравенство се умножат по един и същи числов израз, който има смисъл и положителна стойност, тогава също получаваме истинско числено неравенство. 3.
Ако умножим двете части на едно истинско числено неравенство по един и същи числов израз, който има значима и отрицателна стойност, и също така променим знака на неравенството на противоположния, тогава също получаваме истинско числено неравенство. Упражнения 1.
Определете кои от следните числени равенства и неравенства са верни: а) (5,05: 1/40 - 2,8 ·5/6) ·3 +16·0,1875 = 602; б) (1/14 – 2/7) : (-3) – 6 1/13: (-6 1/13)> (7- 8 4/5) 2 7/9 – 15: (1/8 – 3/4); в) 1,0905:0,025 - 6,84·3,07 + 2,38:100< 4,8:(0,04·0,006). 2.
Проверете дали са верни числовите равенства: 13 93 = 31 39, 14 82 = 41 28, 23 64 = 32 46. Може ли да се каже, че произведението на произволни две естествени числа няма да се промени, ако цифрите във всеки множител се пренаредят ? 3.
Известно е, че x > y -истинско неравенство. Верни ли са следните неравенства: а )2x > 2y; V ) 2x-7< 2у-7;
б)- х/3<-г/3; Ж )-2x-7<-2у-7?
4.
Известно е, че А< б-истинско неравенство. Заменете * с ">" или "<» так, чтобы получилось истинное неравенство: а) -3,7 а * -3,7b; G) - а/3 * -b/3 ; б) 0,12 А * 0,12b; д) -2(a + 5) * -2(b + 5); V) а/7 * b/7; д) 2/7 ( а-1) * 2/7 (b-1). 5.
Дадено е неравенството 5 > 3. Умножете двете страни по 7; 0,1; 2.6; 3/4. Въз основа на получените резултати може ли да се каже, че за всяко положително число Анеравенство 5а> 3Авярно? 6.
Изпълнете задачи, предназначени за ученици от началното училище, и направете заключение как се тълкуват понятията числено равенство и числово неравенство в началния курс по математика. Два числови математически израза, свързани със знака „=“, се наричат равенство. Например: 3 + 7 = 10 - равенство. Равенството може да бъде вярно или невярно. Смисълът на решаването на всеки пример е да се намери стойност на израза, която го превръща в истинско равенство. За формиране на представи за верни и неверни равенства се използват примери с прозорец в учебника за 1. клас. Например: Чрез метода на подбор детето намира подходящи числа и проверява точността на равенството чрез изчисление. Процесът на сравняване на числа и посочване на връзките между тях с помощта на знаци за сравнение води до неравенства. Например: 5< 7; б
>4 - числени неравенства Неравенствата също могат да бъдат верни или неверни. Например: Използвайки метода за подбор, детето намира подходящи числа и проверява точността на неравенството. Числените неравенства се получават чрез сравняване на числови изрази и числа. Например: При избора на знак за сравнение детето изчислява стойността на израза и го сравнява с дадено число, което се отразява в избора на съответния знак: 10-2>7 5+K7 7 + 3>9 6-3 = 3 Възможен е и друг начин за избор на знак за сравнение - без препратка към изчисляване на стойността на израза. Напимеп: Сумата от числата 7 и 2 очевидно ще бъде по-голяма от числото 7, което означава 7 + 2 > 7. Разликата между числата 10 и 3 очевидно ще бъде по-малка от числото 10, което означава 10 - 3< 10. Числените неравенства се получават чрез сравняване на два числови израза. Да сравниш два израза означава да сравниш техните значения. Например: При избора на знак за сравнение детето изчислява значенията на изразите и ги сравнява, което се отразява в избора на съответния знак: Възможен е и друг начин за избор на знак за сравнение - без препратка към изчисляване на стойността на израза. Например: За да зададете знаци за сравнение, можете да извършите следното разсъждение: Сборът на числата 6 и 4 е по-голям от сбора на числата 6 и 3, тъй като 4 > 3, което означава 6 + 4 > 6 + 3. Разликата между числата 7 и 5 е по-малка от разликата между числата 7 и 3, тъй като 5 > 3, което означава 7 - 5< 7 - 3. Частното на 90 и 5 е по-голямо от частното на 90 и 10, защото при разделянето на същото число на по-голямо число, частното е по-малко, което означава 90: 5 > 90:10. За формиране на представи за верни и неверни равенства и неравенства в новото издание на учебника (2001) се използват задачи от вида: За проверка се използва методът за изчисляване на значението на изразите и сравняване на получените числа. Неравенствата с променлива практически не се използват в последните издания на стабилния учебник по математика, въпреки че присъстваха в по-ранните издания. Неравенствата с променливи се използват активно в алтернативните учебници по математика. Това са неравенства от вида: + 7 < 10; 5 - >2; > 0; > О След въвеждането на буква за означаване на неизвестно число, такива неравенства приемат познатата форма на неравенства с променлива: а + 7>10; 12-г<7. Стойностите на неизвестните числа в такива неравенства се намират чрез селекция и след това всяко избрано число се проверява чрез заместване. Особеността на тези неравенства е, че могат да бъдат избрани няколко числа, които им пасват (давайки правилното неравенство). Например: a + 7 > 10; a = 4, a = 5, a = 6 и т.н. - броят на стойностите за буквата a е безкраен, всяко число a> 3 е подходящо за това неравенство; 12 - d< 7; d
= 6, d
= 7, d
= 8, d
= 9, d
= 10, d
= 11, d
= 12 - количество значений для буквы d
конечно, все значения могут быть
перечислены. Ребенок подставляет каждое
найденное значение переменной в
выражение, вычисляет значение выражения
и сравнивает его с заданным числом.
Выбираются те значения переменной, при
которых неравенство является верным. В случай на безкраен брой решения или голям брой решения на неравенство, детето е ограничено до избор на няколко стойности на променливата, за която неравенството е вярно.Понятие за равенство

Свойства на числовите равенства

Понятие за пропорция

Идентичности



5 начина за доказване на самоличност

Основни свойства на идентичностите
Формули за съкратено умножение
Уравнения
4 начина за решаване на уравнение