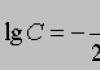Диференциални уравнения.

Основни понятия за обикновените диференциални уравнения.

Определение 1.Обикновено диференциално уравнение н– та поръчка за функцията г аргумент х се нарича отношение на формата

Където Е – дадена функция на неговите аргументи. В името на този клас математически уравнения терминът „диференциал“ подчертава, че те включват производни (функции, образувани в резултат на диференциация); терминът "обикновен" показва, че желаната функция зависи само от един реален аргумент.

Едно обикновено диференциално уравнение може да не съдържа явен аргумент х, желаната функция и всяка от нейните производни, но най-голямата производна трябва да бъде включена в уравнението н-та поръчка. Например

а) – уравнение от първи ред;

б) – уравнение от трети ред.

Когато се записват обикновени диференциални уравнения, често се използва обозначението за производни по отношение на диференциали:

V) – уравнение от втори ред;

г) – уравнение от първи ред,

генератор след деление на dxеквивалентна форма на уточняване на уравнението: .

Функция се нарича решение на обикновено диференциално уравнение, ако при заместване в него се превръща в идентичност.

Например уравнение от 3-ти ред

Има решение .

Намирането по един или друг метод, например селекция, на една функция, която удовлетворява уравнението, не означава решаването му. Да се ​​реши обикновено диференциално уравнение означава да се намери всичкофункции, които образуват идентичност, когато се заместват в уравнение. За уравнение (1.1) семейство от такива функции се формира с помощта на произволни константи и се нарича общо решение на обикновено диференциално уравнение н-ти ред и броят на константите съвпада с реда на уравнението: Общото решение може да бъде, но не е изрично разрешено по отношение на y(x): В този случай решението обикновено се нарича общ интеграл на уравнение (1.1).

Например общото решение на диференциално уравнение е следният израз: , а вторият член може да бъде записан като , тъй като произволна константа, разделена на 2, може да бъде заменена с нова произволна константа.

Присвоявайки някои допустими стойности на всички произволни константи в общото решение или в общия интеграл, получаваме определена функция, която вече не съдържа произволни константи. Тази функция се нарича частично решение или частичен интеграл на уравнение (1.1). За да се намерят стойностите на произволни константи и следователно конкретно решение, се използват различни допълнителни условия към уравнение (1.1). Например, така наречените начални условия могат да бъдат определени в (1.2)

От дясната страна на началните условия (1.2) са посочени числените стойности на функцията и производните, а общият брой на началните условия е равен на броя на дефинираните произволни константи.

Проблемът за намиране на определено решение на уравнение (1.1) въз основа на началните условия се нарича проблем на Коши.

§ 2. Обикновени диференциални уравнения от 1-ви ред - основни понятия.

Обикновено диференциално уравнение от 1-ви ред ( н=1) има формата: или, ако може да се разреши по отношение на производната: . Общо решение y=y(x,С) или общият интеграл на уравненията от 1-ви ред съдържат една произволна константа. Единственото начално условие за уравнение от 1-ви ред ви позволява да определите стойността на константата от общо решение или от общ интеграл. Така ще бъде намерено конкретно решение или, което е същото, проблемът на Коши ще бъде решен. Въпросът за съществуването и уникалността на решението на задачата на Коши е един от централните в общата теория на обикновените диференциални уравнения. По-специално за уравнение от 1-ви ред е валидна теоремата, която тук се приема без доказателство.

Теорема 2.1.Ако в уравнението функцията и нейната частна производна са непрекъснати в някаква област д самолет XOY и в тази област е дадена точка, тогава има уникално решение, което удовлетворява както уравнението, така и началното условие.

Геометрично, общото решение на уравнение от 1-ви ред е семейство от криви в равнината XOY, нямащи общи точки и различаващи се един от друг по един параметър - стойността на константата ° С. Тези криви се наричат ​​интегрални криви за дадено уравнение. Кривите на интегралното уравнение имат очевидно геометрично свойство: във всяка точка допирателната на допирателната към кривата е равна на стойността на дясната страна на уравнението в тази точка: . С други думи, уравнението е дадено в равнината XOYполе от посоки на допирателни към интегрални криви. коментар:Трябва да се отбележи, че към ур. уравнението и т. нар. уравнение са дадени в симетрична форма .

Диференциални уравнения от първи ред с разделими променливи.

Определение.Диференциално уравнение с разделими променливи е уравнение на формата (3.1)

или уравнение от вида (3.2)

За да се разделят променливите в уравнение (3.1), т.е. редуцирайте това уравнение до така нареченото уравнение с отделена променлива, направете следното:

;

Сега трябва да решим уравнението g(y)= 0. Ако има реално решение y=a, Че y=aсъщо ще бъде решение на уравнение (3.1).

Уравнение (3.2) се свежда до отделно уравнение чрез разделяне на произведението:

, което ни позволява да получим общия интеграл на уравнение (3.2): . (3.3)

Интегралните криви (3.3) ще бъдат допълнени с решения, ако такива съществуват.

Решете уравнението: .

Разделяме променливите:

.

Интегрирайки, получаваме

Нека разгледаме примери за решаване на диференциални уравнения с разделими променливи.

1) Интегрирайте диференциалното уравнение: (1+x²)dy-2xydx=0.

Това уравнение е разделимо уравнение, написано като

Оставяме члена с dy от лявата страна на уравнението и преместваме члена с dx в дясната страна:

(1+x²)dy = 2xydx

Разделяме променливите, тоест оставяме само dy от лявата страна и всичко, което съдържа y от дясната страна, dx и x. За да направите това, разделете двете страни на уравнението на (1+x²) и на y. Получаваме

Нека интегрираме двете страни на уравнението:

От лявата страна е интегрална маса. Интегралът от дясната страна може да бъде намерен, например, като направите замяната t=1+x², тогава

dt=(1+x²)’dx=2xdx.

В примери, където е възможно да се извърши потенциране, тоест да се премахнат логаритми, е удобно да се вземе не C, а lnC. Точно това ще направим: ln│y│=ln│t│+ln│C│. Тъй като сумата от логаритми е равна на логаритъма от произведението, тогава ln│y│=ln│Сt│, откъдето y=Ct. Правим обратната промяна и получаваме общото решение: y=C(1+x²).

Разделихме на 1+x² и на y, при условие че не са равни на нула. Но 1+x² не е равно на нула за нито едно x. И y=0 при C=0, следователно не е настъпила загуба на корени.

Отговор: y=C(1+x²).

2) Намерете общия интеграл на уравнението

Променливите могат да бъдат разделени.

Умножете двете страни на уравнението по dx и разделете на

Получаваме:

Сега нека се интегрираме

От лявата страна е интегрална маса. Вдясно - правим замяната 4-x²=t, след това dt=(4-x²)’dx=-2xdx. Получаваме

Ако вместо C вземем 1/2 ln│C│, можем да напишем отговора по-компактно:

Нека умножим двете страни по 2 и приложим свойството на логаритъма:

Разделихме на

Те не са равни на нула: y²+1 - тъй като сумата на неотрицателните числа не е равна на нула, а радикалният израз не е равен на нула по смисъла на условието. Това означава, че не е имало загуба на корени.

3) а) Намерете общия интеграл на уравнението (xy²+y²)dx+(x²-x²y)dy=0.

b) Намерете частичния интеграл на това уравнение, което удовлетворява началното условие y(e)=1.

a) Трансформирайте лявата страна на уравнението: y²(x+1)dx+x²(1-y)dy=0, след това

y²(x+1)dx=-x²(1-y)dy. Разделяме двете страни на x²y², при условие че нито x, нито y са равни на нула. Получаваме:

Нека интегрираме уравнението:

Тъй като разликата на логаритмите е равна на логаритъма на частното, имаме:

Това е общият интеграл на уравнението. В процеса на решаване поставяме условието произведението x²y² да не е равно на нула, което означава, че x и y не трябва да са равни на нула. Като заместим x=0 и y=0 в условието: (0,0²+0²)dx+(0²-0²0)dy=0, получаваме правилното равенство 0=0. Това означава, че x=0 и y=0 също са решения на това уравнение. Но те не са включени в общия интеграл за всяко C (нули не могат да се появяват под знака на логаритъма и в знаменателя на дробта), така че тези решения трябва да бъдат записани в допълнение към общия интеграл.

б) Тъй като y(e)=1, заместваме x=e, y=1 в полученото решение и намираме C:

Примери за самотест:

В цяла поредица от обикновени диференциални уравнения от първи ред има такива, в които променливите x и y могат да бъдат разделени на дясната и лявата страна на уравнението. Променливите може вече да са разделени, както може да се види в уравнението f(y)d y = g(x)dx. Можете да разделите променливите в ODE f 1 (y) · g 1 (x) d y = f 2 (y) · g 2 (x) d x чрез извършване на трансформации. Най-често за получаване на уравнения с разделими променливи се използва методът за въвеждане на нови променливи.

В тази тема ще разгледаме подробно метода за решаване на уравнения с разделени променливи. Нека разгледаме уравнения с разделими променливи и диференциални уравнения, които могат да бъдат сведени до уравнения с разделими променливи. В този раздел сме анализирали голям брой проблеми по темата с подробен анализ на решението.

За да улесните усвояването на темата, ви препоръчваме да се запознаете с информацията, публикувана на страницата „Основни дефиниции и понятия от теорията на диференциалните уравнения“.

Разделени диференциални уравнения f (y) d y = g (x) d x

Уравнения с разделени променливи се наричат ​​диференциални уравнения от формата f (y) d y = g (x) d x. Както подсказва името, променливите, които съставят израз, са от двете страни на знака за равенство.

Нека се съгласим, че функциите f (y) и g(x)ще приемем непрекъснато.

За уравнения с разделени променливи общият интеграл ще бъде ∫ f (y) d y = ∫ g (x) d x. Можем да получим общо решение на диференциалното уравнение под формата на неявно зададена функция Ф (x, y) = 0, при условие че интегралите от горното равенство са изразени в елементарни функции. В някои случаи е възможно да се изрази функцията y в ясна форма.

Пример 1

Намерете общото решение на отделеното диференциално уравнение y 2 3 d y = sin x d x .

Решение

Нека интегрираме двете страни на равенството:

∫ y 2 3 d y = ∫ sin x d x

Това всъщност е общото решение на тази система за управление. Всъщност сведохме проблема за намиране на общо решение на диференциалното уравнение до проблема за намиране на неопределени интеграли.

Сега можем да използваме таблицата на първоизводните, за да вземем интеграли, които са изразени в елементарни функции:

∫ y 2 3 d y = 3 5 y 5 3 + C 1 ∫ sin x d x = - cos x + C 2 ⇒ ∫ y 2 3 d y = ∫ sin x d x ⇔ 3 5 y 3 5 + C 1 = - cos x + C 2
където C1 и C2 са произволни константи.

Функцията 3 5 y 3 5 + C 1 = - cos x + C 2 е указана имплицитно. Това е общо решение на оригиналното диференциално уравнение с разделени променливи. Получихме отговор и може да не продължим с решението. Въпреки това, в разглеждания пример желаната функция може да бъде изразена изрично чрез аргумента x.

Получаваме:

3 5 y 5 3 + C 1 ⇒ y = - 5 3 cos x + C 3 5, където C = 5 3 (C 2 - C 1)

Общото решение на това DE е функцията y = - 5 3 cos x + C 3 5

Отговор:

Можем да запишем отговора по няколко начина: ∫ y 2 3 d y = ∫ sin x d x или 3 5 y 5 3 + C 1 = - cos x + C 2, или y = - 5 3 cos x + C 3 5

Винаги си струва да изясните на учителя, че наред с уменията за решаване на диференциални уравнения вие също имате способността да трансформирате изрази и да взимате интеграли. Лесно е да се направи. Достатъчно е да дадете крайния отговор под формата на явна функция или неявно зададена функция Ф (x, y) = 0.

Диференциални уравнения с разделими променливи f 1 (y) g 1 (x) d y = f 2 (y) g 2 (x) d x

y " = d y d x в случаите, когато y е функция на аргумента x.

В DE f 1 (y) g 1 (x) d y = f 2 (y) g 2 (x) d x или f 1 (y) g 1 (x) y " = f 2 (y) g 2 (x) d x можем да извършим трансформации по такъв начин, че да разделим променливите. Този тип DE се нарича DE с разделими променливи. Съответният DE с разделени променливи ще бъде написан като f 1 (y) f 2 (y) d y = g 2 ( x) g 1 (x) d x .

При разделяне на променливи е необходимо всички трансформации да се извършват внимателно, за да се избегнат грешки. Полученото и първоначалното уравнения трябва да са еквивалентни едно на друго. Като проверка можете да използвате условието, според което f 2 (y) и g 1 (x)не трябва да изчезва на интервала на интегриране. Ако това условие не е изпълнено, тогава има вероятност да загубите някои от решенията.

Пример 2

Намерете всички решения на диференциалното уравнение y " = y · (x 2 + e x) .

Решение

Можем да разделим x и y, следователно имаме работа с диференциално уравнение с разделими променливи.

y " = y · (x 2 + e x) ⇔ d y d x = y · (x 2 + e x) ⇔ d y y = (x 2 + e x) d x pr и y ≠ 0

Когато y = 0, оригиналното уравнение се превръща в идентичност: 0 " = 0 · (x 2 + e x) ⇔ 0 ≡ 0. Това ще ни позволи да заявим, че y = 0 е решение на DE. Не можахме да приемем това решение при извършване на трансформациите.

Нека извършим интегрирането на диференциалното уравнение с разделени променливи d y y = (x 2 + e x) d x:
∫ d y y = ∫ (x 2 + e x) d x ∫ d y y = ln y + C 1 ∫ (x 2 + e x) d x = x 3 3 + e x + C 2 ⇒ ln y + C 1 = x 3 3 + e x + C 2 ⇒ ln y = x 3 3 + e x + C

При извършване на трансформацията извършихме подмяна C 2 - C 1На СЪС. Решението на DE има формата на имплицитно определена функция ln y = x 3 3 + e x + C . Ние можем да изразим тази функция изрично. За да направим това, нека потенцираме полученото равенство:

ln y = x 3 3 + e x + C ⇔ e ln y = e x 3 3 + e x + C ⇔ y = e x 3 3 + e x + C

Отговор: y = e x 3 3 + e x + C, y = 0

Диференциални уравнения, свеждащи се до уравнения с разделими променливи y " = f (a x + b y), a ≠ 0, b ≠ 0

За да се намали обикновеният DE от първи ред y " = f (a x + b y), a ≠ 0, b ≠ 0, към уравнение с разделими променливи, е необходимо да се въведе нова променлива z = a x + b y, където z е функция на аргумента х.

Получаваме:

z = a x + b y ⇔ y = 1 b (z - a x) ⇒ y " = 1 b (z " - a) f (a x + b y) = f (z)

Извършваме замяната и необходимите трансформации:

y " = f (a x + b y) ⇔ 1 b (z " - a) = f (z) ⇔ z " = b f (z) + a ⇔ d z b f (z) + a = d x , b f (z) + a ≠ 0

Пример 3

Намерете общото решение на диференциалното уравнение y " = 1 ln (2 x + y) - 2 и частно решение, което удовлетворява началното условие y (0) = e.

Решение

Нека въведем променлива z = 2 x + y, получаваме:

y = z - 2 x ⇒ y " = z " - 2 ln (2 x + y) = ln z

Заместваме резултата, който получихме в оригиналния израз и го трансформираме в диференциално уравнение с разделими променливи:

y " = 1 ln (2 x + y) - 2 ⇔ z " - 2 = 1 ln z - 2 ⇔ d z d x = 1 ln z

Нека интегрираме двете страни на уравнението след разделяне на променливите:

d z d z = 1 ln z ⇔ ln z d z = d x ⇔ ∫ ln z d z = ∫ d x

Нека използваме метода на интегриране по части, за да намерим интеграла, разположен от лявата страна на уравнението. Нека разгледаме интеграла от дясната страна в таблицата.

∫ ln z d z = u = ln z , d v = d z d u = d z z , v = z = z ln z - ∫ z d z z = = z ln z - z + C 1 = z (ln z - 1) + C 1 ∫ d x = x + C 2

Можем да заявим, че z · (ln z - 1) + C 1 = x + C 2 . Сега, ако приемем това C = C 2 - C 1и ние ще извършим обратна подмяна z = 2 x + y, тогава получаваме общо решение на диференциалното уравнение под формата на имплицитно зададена функция:

(2 x + y) · (ln (2 x + y) - 1) = x + C

Сега нека започнем да намираме конкретно решение, което трябва да отговаря на първоначалното условие y(0)=e. Да направим замяна х = 0и y (0) = e в общото решение на DE и намерете стойността на константата C.

(2 0 + e) ​​​​(ln (2 0 + e) ​​​​- 1) = 0 + C e (ln e - 1) = C C = 0

Получаваме конкретно решение:

(2 x + y) · (ln (2 x + y) - 1) = x

Тъй като формулировката на проблема не уточнява интервала, през който е необходимо да се намери общо решение на DE, ние търсим решение, което е подходящо за всички стойности на аргумента x, за които оригиналният DE има смисъл.

В нашия случай DE има смисъл за ln (2 x + y) ≠ 0, 2 x + y > 0

Диференциални уравнения, свеждащи се до уравнения с разделими променливи y " = f x y или y " = f y x

Можем да намалим диференциалните уравнения под формата y " = f x y или y " = f y x до разделими диференциални уравнения, като направим заместването z = x y или z = y x , където z– функция на аргумента x.

Ако z = x y, тогава y = x z и според правилото за диференциране на дроби:

y " = x y " = x " z - x z " z 2 = z - x z " z 2

В този случай уравненията ще приемат формата z - x · z " z 2 = f (z) или z - x · z " z 2 = f 1 z

Ако вземем z = y x, тогава y = x ⋅ z и по правилото за производна на продукта y " = (x z) " = x " z + x z " = z + x z ". В този случай уравненията се свеждат до z + x z " = f 1 z или z + x z " = f (z) .

Пример 4

Решете диференциалното уравнение y " = 1 e y x - y x + y x

Решение

Да вземем z = y x, тогава y = x z ⇒ y " = z + x z ". Нека заместим в оригиналното уравнение:

y " = 1 e y x - y x + y x ⇔ z + x z " = 1 e z - z + z ⇔ x d z d x = 1 e z - z ⇔ (e z - z) d z = d x x

Нека интегрираме уравнението с разделени променливи, които получихме при извършване на трансформациите:

∫ (e z - z) d z = ∫ d x x e z - z 2 2 + C 1 = ln x + C 2 e z - z 2 2 = ln x + C , C = C 2 - C 1

Нека извършим обратното заместване, за да получим общото решение на оригиналния DE под формата на имплицитно зададена функция:

e y x - 1 2 y 2 x 2 = ln x + C

Сега нека разгледаме дистанционните управления, които имат формата:

y " = a 0 y n + a 1 y n - 1 x + a 2 y n - 2 x 2 + ... + a n x n b 0 y n + b 1 y n - 1 x + b 2 y n - 2 x 2 + ... + b n x n

Разделяне на числителя и знаменателя на дробта, разположена от дясната страна на записа, на y nили x n, можем да имаме предвид оригиналния DE y " = f x y или y " = f y x

Пример 5

Намерете общото решение на диференциалното уравнение y " = y 2 - x 2 2 x y

Решение

В това уравнение x и y са различни от 0. Това ни позволява да разделим числителя и знаменателя на дробта, разположена от дясната страна на нотацията, на х 2:

y " = y 2 - x 2 2 x y ⇒ y " = y 2 x 2 - 1 2 y x

Ако въведем нова променлива z = y x, получаваме y = x z ⇒ y " = z + x z ".

Сега трябва да заместим в оригиналното уравнение:

y " = y 2 x 2 - 1 2 y x ⇔ z " x + z = z 2 - 1 2 z ⇔ z " x = z 2 - 1 2 z - z ⇔ z " x = z 2 - 1 - 2 z 2 2 z ⇔ d z d x x = - z 2 + 1 2 z ⇔ 2 z d z z 2 + 1 = - d x x

Ето как стигнахме до DE с разделени променливи. Нека намерим решението му:

∫ 2 z d z z 2 + 1 = - ∫ d x x ∫ 2 z d z z 2 + 1 = ∫ d (z 2 + 1) z 2 + 1 = ln z 2 + 1 + C 1 - ∫ d x x = - ln x + C 2 ⇒ ln z 2 + 1 + C 1 = - ln x + C 2

За това уравнение можем да получим явно решение. За да направим това, нека вземем - ln C = C 2 - C 1 и приложим свойствата на логаритъма:

ln z 2 + 1 = - ln x + C 2 - C 1 ⇔ ln z 2 + 1 = - ln x - ln C ⇔ ln z 2 + 1 = - ln C x ⇔ ln z 2 + 1 = ln C x - 1 ⇔ e ln z 2 + 1 = e ln 1 C x ⇔ z 2 + 1 = 1 C x ⇔ z ± 1 C x - 1

Сега извършваме обратното заместване y = x ⋅ z и записваме общото решение на оригиналното диференциално уравнение:

y = ± x 1 C x - 1

В този случай второто решение също би било правилно. Можем да използваме замяната z = x y.Нека разгледаме тази опция по-подробно.

Нека разделим числителя и знаменателя на дробта от дясната страна на уравнението на y 2:

y " = y 2 - x 2 2 x y ⇔ y " = 1 - x 2 y 2 2 x y

Нека z = x y

Тогава y " = 1 - x 2 y 2 2 x y ⇔ z - z " x z 2 = 1 - z 2 2 z

Нека заместим в оригиналното уравнение, за да получим диференциално уравнение с разделими променливи:

y " = 1 - x 2 y 2 2 x y ⇔ z - z " x z 2 = 1 - z 2 2 z

Разделяйки променливите, получаваме равенството d z z (z 2 + 1) = d x 2 x, което можем да интегрираме:

∫ d z z (z 2 + 1) = ∫ d x 2 x

Ако разширим интегранта на интегралната функция ∫ d z z (z 2 + 1) в прости дроби, получаваме:

∫ 1 z - z z 2 + 1 d z

Нека извършим интегрирането на прости дроби:

∫ 1 z - z z 2 + 1 d z = ∫ z d z z 2 + 1 = ∫ d t z - 1 2 ∫ d (z 2 + 1) z 2 + 1 = = ln z - 1 2 ln z 2 + 1 + C 1 = ln z z 2 + 1 + C 1

Сега нека намерим интеграла ∫ d x 2 x:

∫ d x 2 x = 1 2 ln x + C 2 = ln x + C 2

В резултат на това получаваме ln z z 2 + 1 + C 1 = ln x + C 2 или ln z z 2 + 1 = ln C x, където ln C = C 2 - C 1.

Нека извършим обратното заместване z = x y и необходимите трансформации, получаваме:

y = ± x 1 C x - 1

Вариантът на решение, в който заменихме z = x y, се оказа по-трудоемък, отколкото в случай на замяна z = y x. Това заключение ще бъде валидно за голям брой уравнения от вида y " = f x y или y " = f y x . Ако избраният вариант за решаване на такива уравнения се окаже трудоемък, можете да въведете променливата z = y x вместо да замените z = x y. Това по никакъв начин няма да повлияе на резултата.

Диференциални уравнения, свеждащи се до уравнения с разделими променливи y " = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2, a 1, b 1, c 1, a 2, b 2, c 2 ∈ Р

Диференциалните уравнения y " = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 могат да бъдат сведени до уравненията y " = f x y или y " = f y x , следователно до уравнения с разделими променливи. За да направите това, намерете (x 0 , y 0) - решение на система от две линейни хомогенни уравнения a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0 и новите променливи са въведени u = x - x 0 v = y - y 0. След тази замяна уравнението ще приеме формата d v d u = a 1 u + b 1 v a 2 u + b 2 v.

Пример 6

Намерете общото решение на диференциалното уравнение y " = x + 2 y - 3 x - 1 .

Решение

Съставяме и решаваме система от линейни уравнения:

x + 2 y - 3 = 0 x - 1 = 0 ⇔ x = 1 y = 1

Нека променим променливите:

u = x - 1 v = y - 1 ⇔ x = u + 1 y = v + 1 ⇒ d x = d u d y = d v

След заместване в първоначалното уравнение получаваме d y d x = x + 2 y - 3 x - 1 ⇔ d v d u = u + 2 v u . След разделяне на uчислителя и знаменателя на дясната страна имаме d v d u = 1 + 2 v u .

Въвеждаме нова променлива z = v u ⇒ v = z · y ⇒ d v d u = d z d u · u + z, тогава

d v d u = 1 + 2 v u ⇔ d z d u · u + z = 1 + 2 z ⇔ d z 1 + z = d u u ⇒ ∫ d z 1 + z = ∫ d u u ⇔ ln 1 + z + C 1 = ln u + C 2 ⇒ ln 1 + z = ln u + ln C, ln C = C 2 - C 1 ln 1 + z = ln C u 1 + z = C u ⇔ z = C u - 1 ⇔ v u = C u - 1 ⇔ v = u ( C u - 1)

Връщаме се към първоначалните променливи, като правим обратното заместване u = x - 1 v = y - 1:
v = u (C u - 1) ⇔ y - 1 = (x - 1) (C (x - 1) - 1) ⇔ y = C x 2 - (2 C + 1) x + C + 2

Това е общото решение на диференциалното уравнение.

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

Диференциални уравнения от първи ред. Примери за решения.
Диференциални уравнения с разделими променливи

Диференциални уравнения (DE). Тези две думи обикновено ужасяват обикновения човек. Диференциалните уравнения изглеждат нещо непосилно и трудно за овладяване за много ученици. Уууууу... диференциални уравнения, как да преживея всичко това?!

Това мнение и това отношение е коренно погрешно, защото в действителност ДИФЕРЕНЦИАЛНИ УРАВНЕНИЯ – ПРОСТО Е И ДОРИ ЗАБАВНО. Какво трябва да знаете и да можете, за да се научите да решавате диференциални уравнения? За да изучавате успешно дифузи, трябва да сте добри в интегрирането и диференцирането. Колкото по-добре се изучават темите Производна на функция на една променливаИ Неопределен интеграл, толкова по-лесно ще бъде разбирането на диференциалните уравнения. Ще кажа повече, ако имате повече или по-малко прилични умения за интеграция, тогава темата е почти овладяна! Колкото повече интеграли от различни видове можете да решите, толкова по-добре. Защо? Ще трябва да интегрирате много. И разграничете. Също горещо препоръчвамнаучете се да намирате.

В 95% от случаите тестовите работи съдържат 3 вида диференциални уравнения от първи ред: разделими уравнениякоито ще разгледаме в този урок; хомогенни уравненияИ линейни нееднородни уравнения. За тези, които започват да изучават дифузори, ви съветвам да прочетете уроците точно в този ред и след като изучите първите две статии, няма да навреди да консолидирате уменията си в допълнителен семинар - уравнения, свеждащи се до хомогенни.

Има още по-редки видове диференциални уравнения: общи диференциални уравнения, уравнения на Бернули и някои други. Най-важният от последните два типа са уравнения в общи диференциали, тъй като в допълнение към това диференциално уравнение обмислям нов материал - частична интеграция.

Ако ви остават само ден-два, Че за ултра бързо приготвянеИма блиц курсв pdf формат.

И така, ориентирите са поставени - да тръгваме:

Първо, нека си припомним обичайните алгебрични уравнения. Те съдържат променливи и числа. Най-простият пример:. Какво означава да решиш обикновено уравнение? Това означава намиране набор от числа, които удовлетворяват това уравнение. Лесно се забелязва, че уравнението на децата има един корен: . Просто за забавление, нека проверим и заместим намерения корен в нашето уравнение:

– получено е правилното равенство, което означава, че решението е намерено правилно.

Дифузорите са проектирани почти по същия начин!

Диференциално уравнение първа поръчкаобщо взето съдържа:
1) независима променлива;
2) зависима променлива (функция);
3) първата производна на функцията: .

В някои уравнения от първи ред може да няма „x“ и/или „y“, но това не е важно - важнода отидете в контролната зала бешепърва производна и не са ималипроизводни от по-високи разряди – и др.

Какво означава ?Решаването на диференциално уравнение означава намиране набор от всички функции, които удовлетворяват това уравнение. Такъв набор от функции често има формата (– произволна константа), която се нарича общо решение на диференциалното уравнение.

Пример 1

Решете диференциално уравнение

Пълни боеприпаси. Откъде да започна решение?

Първо, трябва да пренапишете производната в малко по-различна форма. Припомняме тромавото обозначение, което на мнозина от вас вероятно се е сторило нелепо и ненужно. Това е правилото в дифузьорите!

Във втората стъпка нека да видим дали е възможно отделни променливи?Какво означава да се разделят променливите? Грубо казано, отлявотрябва да си тръгваме само "гърци", А от дясната странаорганизирам само "Х". Разделянето на променливите се извършва с помощта на „училищни“ манипулации: поставянето им извън скоби, прехвърляне на термини от част към част с промяна на знака, прехвърляне на фактори от част към част според правилото за пропорцията и др.

Диференциали и са пълни умножители и активни участници във военните действия. В разглеждания пример променливите лесно се разделят чрез подхвърляне на факторите според правилото за пропорцията:

Променливите са разделени. От лявата страна има само "Y", от дясната страна - само "X".

Следващ етап - интегриране на диференциално уравнение. Просто е, поставяме интеграли от двете страни:

Разбира се, трябва да вземем интеграли. В този случай те са таблични:

Както си спомняме, константа се присвоява на всяка антипроизводна. Тук има два интеграла, но е достатъчно да напишете константата веднъж (тъй като константа + константа все още е равна на друга константа). В повечето случаи се поставя от дясната страна.

Строго погледнато, след като се вземат интегралите, диференциалното уравнение се счита за решено. Единственото нещо е, че нашето "y" не се изразява чрез "x", тоест решението е представено в имплицитноформа. Решението на диференциално уравнение в неявна форма се нарича общ интеграл на диференциалното уравнение. Тоест това е общ интеграл.

Отговорът в тази форма е доста приемлив, но има ли по-добър вариант? Нека се опитаме да получим общо решение.

Моля те, запомнете първата техника, той е много разпространен и често се използва в практически задачи: ако след интегрирането от дясната страна се появи логаритъм, тогава в много случаи (но не винаги!) е препоръчително да напишете константата също под логаритъма. И СИГУРНО е да запишете, ако резултатът е само логаритъм (както в разглеждания пример).

Това е, ВМЕСТОзаписите обикновено са писмени .

Защо е необходимо това? И за да се улесни изразяването на „играта“. Използване на свойството на логаритмите . В такъв случай:

Сега логаритмите и модулите могат да бъдат премахнати:

Функцията е представена изрично. Това е общото решение.

Отговор: общо решение: .

Отговорите на много диференциални уравнения са доста лесни за проверка. В нашия случай това се прави съвсем просто, ние вземаме намереното решение и го диференцираме:

След това заместваме производната в оригиналното уравнение:

– получено е правилното равенство, което означава, че общото решение удовлетворява уравнението, което е необходимо да се провери.

Като зададете константа различни стойности, можете да получите безкраен брой частни решениядиференциално уравнение. Ясно е, че всяка от функциите , и т.н. удовлетворява диференциалното уравнение.

Понякога се извиква общото решение семейство от функции. В този пример общото решение е семейство от линейни функции или по-точно семейство от права пропорционалност.

След задълбочен преглед на първия пример е подходящо да отговорите на няколко наивни въпроса относно диференциалните уравнения:

1)В този пример успяхме да разделим променливите. Може ли това винаги да се прави?Не винаги. И още по-често променливите не могат да бъдат разделени. Например в хомогенни уравнения от първи ред, първо трябва да го смените. В други видове уравнения, например в линейно нехомогенно уравнение от първи ред, трябва да използвате различни техники и методи, за да намерите общо решение. Уравненията с разделими променливи, които разглеждаме в първия урок, са най-простият тип диференциални уравнения.

2) Винаги ли е възможно да се интегрира диференциално уравнение?Не винаги. Много е лесно да се измисли „фантастично“ уравнение, което не може да бъде интегрирано; освен това има интеграли, които не могат да бъдат взети. Но такива DE могат да бъдат решени приблизително с помощта на специални методи. Д’Аламбер и Коши гарантират... ...уф, луркмор.за да прочета много току-що, почти добавих „от онзи свят“.

3) В този пример получихме решение под формата на общ интеграл . Винаги ли е възможно да се намери общо решение от общ интеграл, тоест да се изрази изрично „y“?Не винаги. Например: . Е, как ще изразиш тук "гръцки"?! В такива случаи отговорът трябва да се запише като общ интеграл. Освен това понякога е възможно да се намери общо решение, но то е написано толкова тромаво и тромаво, че е по-добре да оставим отговора под формата на общ интеграл

4) ...може би това е достатъчно за сега. В първия пример, който срещнахме друг важен момент, но за да не покривам „манекените“ с лавина от нова информация, ще го оставя за следващия урок.

Няма да бързаме. Друго просто дистанционно управление и друго типично решение:

Пример 2

Намерете конкретно решение на диференциалното уравнение, което удовлетворява началното условие

Решение: според състоянието, трябва да намерите частно решение DE, който отговаря на дадено начално условие. Тази постановка на въпроса се нарича още Проблем с Коши.

Първо намираме общо решение. В уравнението няма променлива „x“, но това не трябва да обърква, основното е, че има първата производна.

Пренаписваме производната в необходимата форма:

Очевидно променливите могат да бъдат разделени, момчета отляво, момичета отдясно:

Нека интегрираме уравнението:

Получава се общият интеграл. Тук съм нарисувал константа със звездичка, факт е, че много скоро тя ще се превърне в друга константа.

Сега се опитваме да трансформираме общия интеграл в общо решение (изразете изрично „y“). Да си припомним добрите стари неща от училище: . В такъв случай:

Константата в индикатора изглежда някак некошерна, така че обикновено се сваля на земята. В детайли така става. Използвайки свойството на степените, пренаписваме функцията, както следва:

Ако е константа, тогава е и някаква константа, нека я преозначим с буквата:
– в този случай премахваме модула, след което константата “ce” може да приема както положителни, така и отрицателни стойности

Не забравяйте, че „разрушаването“ е константа втора техника, който често се използва при решаване на диференциални уравнения. На чистата версия можете веднага да преминете от към, но винаги бъдете готови да обясните този преход.

И така, общото решение е: . Това е хубаво семейство от експоненциални функции.

На последния етап трябва да намерите конкретно решение, което да отговаря на даденото начално условие. Това също е просто.

Каква е задачата? Трябва да вземете такивастойността на константата, така че условието да е изпълнено.

Може да се форматира по различни начини, но това вероятно ще бъде най-ясният начин. В общото решение вместо „X“ заместваме нула, а вместо „Y“ заместваме две:



Това е,

Стандартна версия на дизайна:

Сега заместваме намерената стойност на константата в общото решение:
– това е конкретното решение, от което се нуждаем.

Отговор: лично решение:

Да проверим. Проверката на частно решение включва два етапа:

Първо трябва да проверите дали конкретното намерено решение наистина удовлетворява първоначалното условие? Вместо „X“ заместваме нула и вижте какво се случва:
- да, наистина е получена двойка, което означава, че първоначалното условие е изпълнено.

Вторият етап вече е познат. Взимаме полученото конкретно решение и намираме производната:

Заместваме в оригиналното уравнение:

– получава се правилното равенство.

Заключение: конкретното решение е намерено правилно.

Да преминем към по-смислени примери.

Пример 3

Решете диференциално уравнение

Решение:Пренаписваме производната във формата, от която се нуждаем:

Оценяваме дали е възможно да разделим променливите? Мога. Преместваме втория член от дясната страна с промяна на знака:

И прехвърляме множителите според правилото на пропорцията:

Променливите са разделени, нека интегрираме двете части:

Трябва да ви предупредя, че денят на страшния съд наближава. Ако не сте учили добре неопределени интеграли, са решили няколко примера, тогава няма къде да отидете - ще трябва да ги усвоите сега.

Интегралът на лявата страна е лесен за намиране; ние се занимаваме с интеграла на котангенса, използвайки стандартната техника, която разгледахме в урока Интегриране на тригонометрични функцииминалата година:

В резултат на това получихме само логаритми и, според първата ми техническа препоръка, ние също определяме константата като логаритъм.

Сега се опитваме да опростим общия интеграл. Тъй като имаме само логаритми, е напълно възможно (и необходимо) да се отървем от тях. Като се използва известни свойства„Паковаме“ логаритмите колкото е възможно повече. Ще го напиша много подробно:

Опаковката е варварски оръфана:
, и веднага представяме общ интегралМежду другото, стига това да е възможно:

Най-общо казано, не е необходимо да се прави това, но винаги е полезно да се угоди на професора ;-)

По принцип този шедьовър може да се напише като отговор, но тук все пак е уместно да поставим на квадрат и двете части и да обозначим отново константата:

Отговор:общ интеграл:

! Забележка: Общият интеграл често може да бъде написан по повече от един начин. Следователно, ако вашият резултат не съвпада с предварително известния отговор, това не означава, че сте решили уравнението неправилно.

Може ли да се изрази „игра“? Мога. Нека изразим общото решение:

Разбира се, полученият резултат е подходящ за отговор, но имайте предвид, че общият интеграл изглежда по-компактен, а решението е по-кратко.

Трети технически съвет:ако за да получите общо решение, трябва да извършите значителен брой действия, тогава в повечето случаи е по-добре да се въздържате от тези действия и да оставите отговора под формата на общ интеграл. Същото важи и за „лошите“ действия, когато трябва да изразите обратната функция, да повдигнете на степен, да извлечете корена и т.н.Факт е, че общото решение ще изглежда претенциозно и тромаво - с големи корени, знаци и други математически боклуци.

Как да проверя? Проверката може да се извърши по два начина. Първи метод: вземете общото решение , намираме производната и ги заместете в първоначалното уравнение. Опитайте сами!

Вторият начин е да се диференцира общият интеграл. Това е доста лесно, най-важното е да можете да намерите производна на функция, зададена имплицитно:

разделете всеки член на:

и на:

Оригиналното диференциално уравнение е получено точно, което означава, че общият интеграл е намерен правилно.

Пример 4

Намерете конкретно решение на диференциалното уравнение, което удовлетворява началното условие. Извършете проверка.

Това е пример, който можете да решите сами.

Нека ви напомня, че алгоритъмът се състои от два етапа:
1) намиране на общо решение;
2) намиране на необходимото конкретно решение.

Проверката също се извършва на две стъпки (вижте примера в Пример № 2), трябва да:
1) уверете се, че конкретното намерено решение отговаря на първоначалното условие;
2) проверете дали определено решение като цяло удовлетворява диференциалното уравнение.

Пълно решение и отговор в края на урока.

Пример 5

Намерете конкретно решение на диференциалното уравнение , отговарящи на началното условие. Извършете проверка.

Решение:Първо, нека намерим общо решение.Това уравнение вече съдържа готови диференциали и следователно решението е опростено. Разделяме променливите:

Нека интегрираме уравнението:

Интегралът отляво е табличен, интегралът отдясно е взет метод за поставяне на функция под диференциалния знак:

Общият интеграл е получен; възможно ли е успешно да се изрази общото решение? Мога. Закачаме логаритми от двете страни. Тъй като те са положителни, модулните знаци са ненужни:

(Надявам се всички да разберат трансформацията, такива неща вече трябва да се знаят)

И така, общото решение е:

Нека намерим конкретно решение, отговарящо на даденото начално условие.
В общото решение вместо „X“ заместваме нула, а вместо „Y“ заместваме логаритъма от две:

По-познат дизайн:

Заместваме намерената стойност на константата в общото решение.

Отговор:лично решение:

Проверка: Първо, нека проверим дали е изпълнено първоначалното условие:
- всичко е наред.

Сега нека проверим дали намереното конкретно решение изобщо удовлетворява диференциалното уравнение. Намиране на производната:

Нека да разгледаме оригиналното уравнение: – представя се в диференциали. Има два начина за проверка. Възможно е да се изрази диференциала от намерената производна:

Нека заместим намереното конкретно решение и получения диференциал в първоначалното уравнение :

Използваме основната логаритмична идентичност:

Получава се правилното равенство, което означава, че конкретното решение е намерено правилно.

Вторият метод за проверка е огледален и по-познат: от уравнението Нека изразим производната, за да направим това, разделяме всички части на:

И в преобразуваното DE заместваме полученото частично решение и намерената производна. В резултат на опростявания трябва да се получи и правилното равенство.

Пример 6

Намерете общия интеграл на уравнението, представете отговора във формуляра.

Това е пример, който можете да решите сами, пълно решение и отговор в края на урока.

Какви трудности чакат при решаването на диференциални уравнения с разделими променливи?

1) Не винаги е очевидно (особено за „чайник“), че променливите могат да бъдат разделени. Нека разгледаме един условен пример: . Тук трябва да извадите факторите от скоби: и да разделите корените: . Ясно е какво да правим по-нататък.

2) Трудности със самата интеграция. Интегралите често не са най-простите и ако има недостатъци в уменията за намиране неопределен интеграл, тогава ще е трудно с много дифузори. В допълнение, логиката „тъй като диференциалното уравнение е просто, тогава поне нека интегралите да бъдат по-сложни“ е популярна сред съставителите на колекции и ръководства за обучение.

3) Трансформации с константа. Както всички са забелязали, константата в диференциалните уравнения може да се борави доста свободно и някои трансформации не винаги са ясни за начинаещ. Нека да разгледаме друг условен пример: . Препоръчително е да умножите всички термини по 2: . Получената константа също е някакъв вид константа, която може да бъде означена с: . Да, и тъй като имаме само логарими, препоръчително е да пренапишем константата под формата на друга константа: .

Проблемът е, че те често не се занимават с индекси и използват една и съща буква. В резултат на това записът на решението приема следната форма:

Какво за Бога?! Точно там има грешки! Строго погледнато, да. Но от гледна точка на съдържанието грешки няма, тъй като в резултат на трансформиране на променлива константа се получава еквивалентна променлива константа.

Или друг пример, да предположим, че в хода на решаването на уравнението се получава общ интеграл. Този отговор изглежда грозен, така че е препоръчително да промените знака на всеки термин: . Формално тук има друга грешка - трябва да се пише отдясно. Но неофициално се разбира, че „минус ce“ все още е константа, която също така приема същия набор от стойности и следователно няма смисъл да се поставя „минус“.

Ще се опитам да избегна небрежен подход и все пак ще присвоя различни индекси на константите, когато ги преобразувам. Което ви съветвам да направите.

Пример 7

Решете диференциално уравнение. Извършете проверка.

Решение:Това уравнение позволява разделяне на променливи. Разделяме променливите:

Нека интегрираме:

Не е необходимо да дефинирате константата тук като логаритъм, тъй като нищо полезно няма да излезе от това.

Отговор:общ интеграл:

И, разбира се, няма нужда да изразявате изрично „y“, защото ще се окаже боклук (помнете третия технически съвет).

Преглед: Диференцирайте отговора (имплицитна функция):

Отърваваме се от дроби, като умножим двата члена по:

Получено е оригиналното диференциално уравнение, което означава, че общият интеграл е намерен правилно.

Пример 8

Намерете конкретно решение на DE.
,

Разглежда се метод за решаване на диференциални уравнения с разделими променливи. Даден е пример за подробно решение на диференциално уравнение с разделими променливи.

Определение

Нека да (х), q (х)- функции на променливата x;
стр (y), r (y)- функции на променливата y.

Диференциално уравнение с разделими променливи е уравнение на формата

Метод за решаване на диференциално уравнение с разделими променливи

Разгледайте уравнението:
(i) .
Нека изразим производната y′ чрез диференциали.
;
.
Нека умножим по dx.
(ii)
Разделете уравнението на s (x)r(y). Това може да стане, ако s (x) r(y) ≠ 0. Когато s (x) r(y) ≠ 0ние имаме
.
Интегрирайки, получаваме общия интеграл в квадратури
(iii) .

Тъй като разделихме на s (x)r(y), тогава получихме интеграла на уравнението за s (x) ≠ 0и r (y) ≠ 0. След това трябва да решите уравнението
r (y) = 0.
Ако това уравнение има корени, тогава те също са решения на уравнение (i). Нека уравнението r (y) = 0. има n корена a i, r (a i ) = 0, i = 1, 2, ... , н. Тогава константите y = a i са решения на уравнение (i). Някои от тези решения може вече да се съдържат в общия интеграл (iii).

Обърнете внимание, че ако първоначалното уравнение е дадено във форма (ii), тогава трябва да решим и уравнението
с (x) = 0.
Корените му b j, s (b j ) = 0, j = 1, 2, ... , м. дават решения x = b j .

Пример за решаване на диференциално уравнение с разделими променливи

Решете уравнението

Нека изразим производната чрез диференциали:


Умножете по dx и разделете на . За y ≠ 0 имаме:

Да се ​​интегрираме.

Изчисляваме интегралите по формулата.



Замествайки, получаваме общия интеграл на уравнението
.

Сега разгледайте случая, y = 0 .
Очевидно y = 0 е решение на първоначалното уравнение. Не се включва в общия интеграл.
Затова ще го добавим към крайния резултат.

; y = 0 .

Препратки:
Н.М. Гюнтер, Р.О. Кузмин, Сборник задачи по висша математика, “Лан”, 2003 г.