Това е последният и най-важен урок, необходим за решаване на задачи B11. Вече знаем как да преобразуваме ъгли от радианова мярка в градусна мярка (вижте урока „Радиан и градусна мярка на ъгъл“), а също така знаем как да определим знака на тригонометрична функция, като се фокусираме върху координатните четвърти ( вижте урока „Знаци на тригонометрични функции“).
Остава само да изчислим стойността на самата функция - точното число, което е записано в отговора. Тук идва на помощ основната тригонометрична идентичност.
Основно тригонометрично тъждество. За всеки ъгъл α е вярно следното твърдение:
sin 2 α + cos 2 α = 1.
Тази формула свързва синуса и косинуса на един ъгъл. Сега, знаейки синуса, можем лесно да намерим косинуса - и обратно. Достатъчно е да вземете корен квадратен:
Обърнете внимание на знака "±" пред корените. Факт е, че от основната тригонометрична идентичност не е ясно какви са били първоначалните синус и косинус: положителни или отрицателни. В крайна сметка квадратурата е равномерна функция, която „изгаря“ всички минуси (ако има такива).
Ето защо във всички задачи B11, които се намират в Единния държавен изпит по математика, задължително има допълнителни условия, които помагат да се отървете от несигурността със знаци. Обикновено това е индикация за координатната четвърт, по която може да се определи знакът.
Внимателен читател вероятно ще попита: „Ами тангенс и котангенс?“ Невъзможно е директно да се изчислят тези функции от горните формули. Има обаче важни следствия от основното тригонометрично тъждество, което вече съдържа тангенси и котангенси. а именно:
Важно следствие: за всеки ъгъл α основната тригонометрична идентичност може да бъде пренаписана както следва:
Тези уравнения се извеждат лесно от основното тъждество - достатъчно е да разделите двете страни на cos 2 α (за да получите тангенса) или на sin 2 α (за да получите котангенса).
Нека разгледаме всичко това с конкретни примери. По-долу са реалните задачи B11, които са взети от пробните версии на Единния държавен изпит по математика 2012 г.
Знаем косинуса, но не знаем синуса. Основното тригонометрично тъждество (в неговата „чиста“ форма) свързва точно тези функции, така че ще работим с него. Ние имаме:
sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 99/100 = 1 ⇒ sin 2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
За да решим задачата, остава да намерим знака на синуса. Тъй като ъгълът α ∈ (π /2; π ), тогава в градусна мярка се записва както следва: α ∈ (90°; 180°).
Следователно ъгълът α лежи във II координатна четвърт - всички синуси там са положителни. Следователно sin α = 0,1.
И така, знаем синуса, но трябва да намерим косинуса. И двете функции са в основната тригонометрична идентичност. Нека заместим:
sin 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Остава да се справим със знака пред дробта. Какво да избера: плюс или минус? По условие ъгъл α принадлежи на интервала (π 3π /2). Нека преобразуваме ъглите от радиани в градуси - получаваме: α ∈ (180°; 270°).
Очевидно това е третата координатна четвърт, където всички косинуси са отрицателни. Следователно cos α = −0,5.
Задача. Намерете tan α, ако е известно следното:
Тангенсът и косинусът са свързани с уравнението, следващо от основната тригонометрична идентичност:
Получаваме: tan α = ±3. Знакът на тангентата се определя от ъгъла α. Известно е, че α ∈ (3π /2; 2π ). Нека преобразуваме ъглите от радиани в градуси - получаваме α ∈ (270°; 360°).
Очевидно това е IV координатна четвърт, където всички тангенси са отрицателни. Следователно tan α = −3.
Задача. Намерете cos α, ако е известно следното:
Отново синусът е известен, а косинусът е неизвестен. Нека запишем основната тригонометрична идентичност:
sin 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
Знакът се определя от ъгъла. Имаме: α ∈ (3π /2; 2π ). Нека преобразуваме ъглите от градуси в радиани: α ∈ (270°; 360°) е IV координатна четвърт, косинусите там са положителни. Следователно cos α = 0,6.
Задача. Намерете sin α, ако е известно следното:
Нека запишем формула, която следва от основната тригонометрична идентичност и директно свързва синус и котангенс:
От тук получаваме, че sin 2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно е, че ъгъл α ∈ (0; π /2). В градусна мярка това се записва по следния начин: α ∈ (0°; 90°) - I координатна четвърт.
И така, ъгълът е в I координатния квадрант - всички тригонометрични функции там са положителни, така че sin α = 0,2.
Статията описва подробно основните тригонометрични тъждества, които установяват връзката между sin, cos, t g, c t g на даден ъгъл. Ако една функция е известна, чрез нея може да се намери друга.
Тригонометрични идентичности, които трябва да бъдат разгледани в тази статия. По-долу показваме пример за тяхното извеждане с обяснение.
sin 2 α + cos 2 α = 1 t g α = sin α cos α, c t g α = cos α sin α t g α c t g α = 1 t g 2 α + 1 = 1 cos 2 α, 1 + c t g 2 α = 1 sin 2 α
Нека поговорим за важна тригонометрична идентичност, която се счита за основа на тригонометрията.
sin 2 α + cos 2 α = 1
Дадените равенства t g 2 α + 1 = 1 cos 2 α, 1 + c t g 2 α = 1 sin 2 α се получават от основното, като двете части се разделят на sin 2 α и cos 2 α. След което получаваме t g α = sin α cos α, c t g α = cos α sin α и t g α · c t g α = 1 - това е следствие от дефинициите на синус, косинус, тангенс и котангенс.
Равенството sin 2 α + cos 2 α = 1 е основното тригонометрично тъждество. За да го докажете, трябва да се обърнете към темата за единичния кръг.
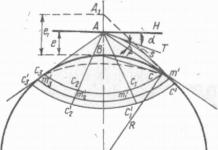
Нека са дадени координатите на точка A (1, 0), която след завъртане на ъгъл α става точка A 1. По дефиниция на sin и cos, точка A 1 ще получи координати (cos α, sin α). Тъй като A 1 се намира в единичната окръжност, това означава, че координатите трябва да отговарят на условието x 2 + y 2 = 1 на тази окръжност. Изразът cos 2 α + sin 2 α = 1 трябва да е валиден. За да направите това, е необходимо да се докаже основната тригонометрична идентичност за всички ъгли на завъртане α.
В тригонометрията изразът sin 2 α + cos 2 α = 1 се използва като Питагоровата теорема в тригонометрията. За да направите това, помислете за подробно доказателство.
Използвайки единична окръжност, завъртаме точка A с координати (1, 0) около централната точка O на ъгъл α. След завъртане точката променя координатите си и става равна на A 1 (x, y). Спускаме перпендикулярната линия A 1 H до O x от точка A 1.
Фигурата ясно показва, че е образуван правоъгълен триъгълник O A 1 N. Модулите на катетите O A 1 N и O N са равни, записът ще приеме следната форма: | A 1 H | = | y | , | О Н | = | x | . Хипотенузата O A 1 има стойност, равна на радиуса на единичната окръжност | O A 1 | = 1. Използвайки този израз, можем да напишем равенството, като използваме Питагоровата теорема: | A 1 N | 2 + | О Н | 2 = | O A 1 | 2. Нека запишем това равенство като | y | 2 + | x | 2 = 1 2, което означава y 2 + x 2 = 1.
Използвайки дефиницията на sin α = y и cos α = x, заместваме данните за ъгъла вместо координатите на точките и преминаваме към неравенството sin 2 α + cos 2 α = 1.
Основната връзка между sin и cos на ъгъл е възможна чрез тази тригонометрична идентичност. Така можем да изчислим греха на ъгъл с известен cos и обратно. За да направите това, е необходимо да разрешите sin 2 α + cos 2 = 1 по отношение на sin и cos, тогава получаваме изрази под формата sin α = ± 1 - cos 2 α и cos α = ± 1 - sin 2 α , съответно. Големината на ъгъла α определя знака пред корена на израза. За подробно обяснение трябва да прочетете раздела за изчисляване на синус, косинус, тангенс и котангенс с помощта на тригонометрични формули.
Най-често основната формула се използва за трансформиране или опростяване на тригонометрични изрази. Възможно е сумата от квадратите на синус и косинус да се замени с 1. Замяната на идентичност може да бъде както в пряк, така и в обратен ред: единицата се заменя с израза на сумата от квадратите на синуса и косинуса.
Тангенс и котангенс през синус и косинус
От дефиницията на косинус и синус, тангенс и котангенс става ясно, че те са взаимосвързани помежду си, което ви позволява отделно да конвертирате необходимите количества.
t g α = sin α cos α c t g α = cos α sin α
От дефиницията синусът е ординатата на y, а косинусът е абсцисата на x. Тангенса е връзката между ординатата и абсцисата. Така имаме:
t g α = y x = sin α cos α , а котангенсният израз има противоположно значение, т.е.
c t g α = x y = cos α sin α .
От това следва, че получените идентичности t g α = sin α cos α и c t g α = cos α sin α са определени с помощта на ъгли sin и cos. Тангенсът се счита за отношението на синуса към косинуса на ъгъла между тях, а котангенсът е обратното.
Имайте предвид, че t g α = sin α cos α и c t g α = cos α sin α са верни за всяка стойност на ъгъл α, чиито стойности са включени в диапазона. От формулата t g α = sin α cos α стойността на ъгъла α е различна от π 2 + π · z, а c t g α = cos α sin α приема стойността на ъгъла α, различна от π · z, z взема стойност на всяко цяло число.
Връзка между тангенс и котангенс
Има формула, която показва връзката между ъглите през тангенс и котангенс. Тази тригонометрична идентичност е важна в тригонометрията и се означава като t g α · c t g α = 1. Има смисъл за α с всякаква стойност, различна от π 2 · z, в противен случай функциите няма да бъдат дефинирани.
Формулата t g α · c t g α = 1 има своите особености в доказателството. От определението имаме, че t g α = y x и c t g α = x y, следователно получаваме t g α · c t g α = y x · x y = 1. Преобразувайки израза и замествайки t g α = sin α cos α и c t g α = cos α sin α, получаваме t g α · c t g α = sin α cos α · cos α sin α = 1.
Тогава изразът на тангенс и котангенс има значението, когато в крайна сметка получаваме взаимно обратни числа.
Тангенс и косинус, котангенс и синус
Преобразувайки основните тъждества, стигаме до извода, че тангенсът е свързан чрез косинус, а котангенсът - чрез синус. Това може да се види от формулите t g 2 α + 1 = 1 cos 2 α, 1 + c t g 2 α = 1 sin 2 α.
Дефиницията е следната: сумата от квадрата на тангенса на ъгъл и 1 се приравнява на дроб, където в числителя имаме 1, а в знаменателя квадрата на косинуса на даден ъгъл и сумата на квадрата на котангенса на ъгъла е обратното. Благодарение на тригонометричната идентичност sin 2 α + cos 2 α = 1, можем да разделим съответните страни на cos 2 α и да получим t g 2 α + 1 = 1 cos 2 α, където стойността на cos 2 α не трябва да е равна на нула. При деление на sin 2 α получаваме идентичността 1 + c t g 2 α = 1 sin 2 α, където стойността на sin 2 α не трябва да е равна на нула.
От горните изрази установихме, че идентичността t g 2 α + 1 = 1 cos 2 α е вярна за всички стойности на ъгъла α, които не принадлежат на π 2 + π · z, и 1 + c t g 2 α = 1 sin 2 α за стойности на α, които не принадлежат на интервал π · z.
Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter
Тригонометрични тъждества- това са равенства, които установяват връзка между синус, косинус, тангенс и котангенс на един ъгъл, което ви позволява да намерите всяка от тези функции, при условие че всяка друга е известна.
\[ \sin^(2)\alpha + \cos^(2) \alpha = 1 \]
\[ tg \alpha = \dfrac(\sin \alpha)(\cos \alpha), \enspace ctg \alpha = \dfrac(\cos \alpha)(\sin \alpha) \]
\[ tg \alpha \cdot ctg \alpha = 1 \]
Връзка между синус и косинус
\[ \sin^(2) \alpha+\cos^(2) \alpha=1 \]
Това тъждество казва, че сборът от квадрата на синуса на един ъгъл и квадрата на косинуса на един ъгъл е равен на едно, което на практика прави възможно изчисляването на синуса на един ъгъл, когато неговият косинус е известен и обратно .
При преобразуване на тригонометрични изрази много често се използва тази идентичност, която ви позволява да замените сумата от квадратите на косинуса и синуса на един ъгъл с единица и също така да извършите операцията за заместване в обратен ред.
Намиране на тангенс и котангенс с помощта на синус и косинус
\[ tg \alpha = \dfrac(\sin \alpha)(\cos \alpha),\enspace ctg \alpha=\dfrac(\cos \alpha)(\sin \alpha) \]
Тези идентичности се формират от дефинициите на синус, косинус, тангенс и котангенс. В крайна сметка, ако го погледнете, тогава по дефиниция ординатата \(\dfrac(y)(x)=\dfrac(\sin \alpha)(\cos \alpha) \), и съотношението \(\dfrac(x)(y)=\dfrac(\cos \alpha)(\sin \alpha) \)- ще бъде котангенс.
Нека добавим, че само за такива ъгли \(\alpha \), при които тригонометричните функции, включени в тях, имат смисъл, идентичностите , .
Например: \(tg \alpha = \dfrac(\sin \alpha)(\cos \alpha) \)е валиден за ъгли \(\alpha \), които са различни от \(\dfrac(\pi)(2)+\pi z \) и \(ctg \alpha=\dfrac(\cos \alpha)(\sin \alpha) \)- за ъгъл \(\alpha \), различен от \(\pi z \) , \(z \) е цяло число.
Връзка между тангенс и котангенс
\[ tg \alpha \cdot ctg \alpha=1 \]
Тази идентичност е валидна само за ъгли \(\alpha \), които са различни от \(\dfrac(\pi)(2) z \) . В противен случай нито котангенсът, нито тангенсът няма да бъдат определени.
Въз основа на горните точки получаваме, че \(tg \alpha = \dfrac(y)(x) \) и \(ctg \alpha=\dfrac(x)(y) \) . Следва, че \(tg \alpha \cdot ctg \alpha = \dfrac(y)(x) \cdot \dfrac(x)(y)=1 \). По този начин тангенсът и котангенсът на същия ъгъл, при който имат смисъл, са взаимно обратни числа.
Връзки между тангенс и косинус, котангенс и синус
\(tg^(2) \alpha + 1=\dfrac(1)(\cos^(2) \alpha) \)- сумата от квадрата на тангенса на ъгъла \(\alpha \) и \(\alpha \), различен от \(\dfrac(\pi)(2)+ \pi z \) .
\(1+ctg^(2) \alpha=\dfrac(1)(\sin^(2)\alpha) \)- сборът \(\alpha \) е равен на обратния квадрат на синуса на даден ъгъл. Тази идентичност е валидна за всяка \(\alpha \), различна от \(\pi z \) .
Javascript е деактивиран във вашия браузър.За да извършвате изчисления, трябва да активирате ActiveX контролите!За решаване на някои проблеми ще бъде полезна таблица с тригонометрични идентичности, което ще направи много по-лесно трансформирането на функции:
Най-простите тригонометрични тъждества
Частното от деленето на синуса на ъгъл алфа на косинуса на същия ъгъл е равно на тангенса на този ъгъл (Формула 1). Вижте също доказателството за коректността на преобразуването на най-простите тригонометрични тъждества.
Частното от деленето на косинуса на ъгъл алфа на синуса на същия ъгъл е равно на котангенса на същия ъгъл (Формула 2)
Секансът на ъгъл е равен на единица, разделена на косинуса на същия ъгъл (Формула 3)
Сборът от квадратите на синуса и косинуса на един и същ ъгъл е равен на едно (Формула 4). вижте също доказателството за сумата от квадратите на косинус и синус.
Сборът от едно и тангенса на ъгъл е равен на съотношението едно към квадрата на косинуса на този ъгъл (Формула 5)
Едно плюс котангенсът на ъгъл е равно на частното от едно, делено на синус квадрат на този ъгъл (Формула 6)
Произведението на тангенса и котангенса на един и същи ъгъл е равно на единица (Формула 7).
Преобразуване на отрицателни ъгли на тригонометрични функции (четни и нечетни)
За да се отървете от отрицателната стойност на градусната мярка на ъгъл при изчисляване на синус, косинус или тангенс, можете да използвате следните тригонометрични трансформации (тъждества), базирани на принципите на четни или нечетни тригонометрични функции.

Както се вижда, косинуси секансът е дори функция, синус, тангенс и котангенс са нечетни функции.
Синусът на отрицателен ъгъл е равен на отрицателната стойност на синуса на същия положителен ъгъл (минус синус алфа).
Косинусът минус алфа ще даде същата стойност като косинуса на ъгъла алфа.
Тангенс минус алфа е равен на минус тангенс алфа.
Формули за намаляване на двойни ъгли (синус, косинус, тангенс и котангенс на двойни ъгли)
Ако трябва да разделите ъгъл наполовина или обратното, да преминете от двоен ъгъл към единичен ъгъл, можете да използвате следните тригонометрични идентичности:

Преобразуване на двоен ъгъл (синус на двоен ъгъл, косинус на двоен ъгъл и тангенс на двоен ъгъл) в единичен се случва съгласно следните правила:
Синус на двоен ъгълравно на удвоеното произведение на синуса и косинуса на един ъгъл
Косинус на двоен ъгълравна на разликата между квадрата на косинуса на отделен ъгъл и квадрата на синуса на този ъгъл
Косинус на двоен ъгълравно на удвоения квадрат на косинуса на отделен ъгъл минус едно
Косинус на двоен ъгълравно на едно минус двоен синус на квадрат на единичен ъгъл
Тангенс на двоен ъгъле равно на дроб, чийто числител е два пъти тангенса на единичен ъгъл, а знаменателят е равен на едно минус тангенса на квадрат на единичен ъгъл.
Котангенс на двоен ъгъле равно на дроб, чийто числител е квадрат на котангенса на отделен ъгъл минус едно, а знаменателят е равен на удвоения котангенс на единичен ъгъл
Формули за универсално тригонометрично заместване
Формулите за преобразуване по-долу могат да бъдат полезни, когато трябва да разделите аргумента на тригонометрична функция (sin α, cos α, tan α) на две и да намалите израза до стойността на половин ъгъл. От стойността на α получаваме α/2.Тези формули се наричат формули за универсално тригонометрично заместване. Тяхната стойност се състои в това, че с тяхна помощ един тригонометричен израз се свежда до изразяване на тангенса на половин ъгъл, независимо какви тригонометрични функции (sin cos tan ctg) са били първоначално в израза. След това уравнението с тангенса на половин ъгъл е много по-лесно за решаване.
Тригонометрични тъждества за полуъглови трансформации
Следват формулите за тригонометрично преобразуване на половин ъгъл в цялата му стойност.Стойността на аргумента на тригонометричната функция α/2 се редуцира до стойността на аргумента на тригонометричната функция α.
Тригонометрични формули за събиране на ъгли

cos (α - β) = cos α cos β + sin α sin β
sin (α + β) = sin α cos β + sin β cos α
sin (α - β) = sin α cos β - sin β cos α
cos (α + β) = cos α cos β - sin α sin β
Тангенс и котангенс на сбора от ъглиалфа и бета могат да бъдат преобразувани, като се използват следните правила за преобразуване на тригонометрични функции:
Тангенс на сбора от ъглие равно на дроб, чийто числител е сумата от тангенса на първия и тангенса на втория ъгъл, а знаменателят е едно минус произведението на тангенса на първия ъгъл и тангенса на втория ъгъл.
Тангенс на ъглова разликае равно на дроб, чийто числител е равен на разликата между тангенса на ъгъла, който се намалява, и тангенса на ъгъла, който се изважда, а знаменателят е едно плюс произведението на тангенсите на тези ъгли.
Котангенс на сбора от ъглие равно на дроб, чийто числител е равен на произведението на котангенсите на тези ъгли плюс едно, а знаменателят е равен на разликата между котангенса на втория ъгъл и котангенса на първия ъгъл.
Котангенс на ъглова разликае равно на дроб, чийто числител е произведението на котангенсите на тези ъгли минус едно, а знаменателят е равен на сбора от котангенсите на тези ъгли.
Тези тригонометрични идентичности са удобни за използване, когато трябва да изчислите, например, тангенса на 105 градуса (tg 105). Ако си го представите като tg (45 + 60), тогава можете да използвате дадените идентични трансформации на тангенса на сумата от ъгли и след това просто да замените табличните стойности на тангентата 45 и тангентата 60 градуса.
Формули за преобразуване на сумата или разликата на тригонометрични функции
Изрази, представляващи сбор от формата sin α + sin β, могат да бъдат трансформирани с помощта на следните формули:
Формули за троен ъгъл - преобразуване sin3α cos3α tan3α в sinα cosα tanα
Понякога е необходимо да се трансформира тройната стойност на ъгъл, така че аргументът на тригонометричната функция да стане ъгъл α вместо 3α.В този случай можете да използвате формулите за трансформация на троен ъгъл (идентичности):

Формули за преобразуване на произведения на тригонометрични функции
Ако има нужда да се преобразува произведението на синуси от различни ъгли, косинуси от различни ъгли или дори произведение от синус и косинус, тогава можете да използвате следните тригонометрични идентичности:
В този случай произведението на функциите синус, косинус или тангенс на различни ъгли ще бъде преобразувано в сбор или разлика.
Формули за редуциране на тригонометрични функции
Трябва да използвате таблицата за намаляване, както следва. В реда избираме функцията, която ни интересува. В колоната има ъгъл. Например синусът на ъгъла (α+90) в пресечната точка на първия ред и първата колона, откриваме, че sin (α+90) = cos α.
Основни тригонометрични тъждества.
secα се чете: „секант алфа“. Това е реципрочната стойност на косинус алфа.
cosecα се чете: „косеканс алфа“. Това е реципрочната стойност на синус алфа.
Примери.Опростете израза:
а) 1 – sin 2 α; б) cos 2 α – 1; V)(1 – cosα)(1+cosα); G) sin 2 αcosα – cosα; д) sin 2 α+1+cos 2 α;
д) sin 4 α+2sin 2 αcos 2 α+cos 4 α; и) tg 2 α – sin 2 αtg 2 α; з) ctg 2 αcos 2 α – ctg 2 α; И) cos 2 α+tg 2 αcos 2 α.
а) 1 – sin 2 α = cos 2 α по формулата 1) ;
б) cos 2 α – 1 =- (1 – cos 2 α) = -sin 2 α също приложи формулата 1) ;
V)(1 – cosα)(1+cosα) = 1 – cos 2 α = sin 2 α. Първо приложихме формулата за разликата на квадратите на два израза: (a – b)(a+b) = a 2 – b 2, а след това формулата 1) ;
G) sin 2 αcosα – cosα. Нека извадим общия множител извън скобите.
sin 2 αcosα – cosα = cosα(sin 2 α – 1) = -cosα(1 – sin 2 α) = -cosα ∙ cos 2 α = -cos 3 α. Вие, разбира се, вече сте забелязали, че тъй като 1 – sin 2 α = cos 2 α, тогава sin 2 α – 1 = -cos 2 α. По същия начин, ако 1 – cos 2 α = sin 2 α, тогава cos 2 α – 1 = -sin 2 α.
д) sin 2 α+1+cos 2 α = (sin 2 α+cos 2 α)+1 = 1+1 = 2;
д) sin 4 α+2sin 2 αcos 2 α+cos 4 α. Имаме: квадрат на израза sin 2 α плюс двойното произведение на sin 2 α по cos 2 α и плюс квадрата на втория израз cos 2 α. Нека приложим формулата за квадрат на сумата от два израза: a 2 +2ab+b 2 =(a+b) 2. След това прилагаме формулата 1) . Получаваме: sin 4 α+2sin 2 αcos 2 α+cos 4 α = (sin 2 α+cos 2 α) 2 = 1 2 = 1;
и) tg 2 α – sin 2 αtg 2 α = tg 2 α(1 – sin 2 α) = tg 2 α ∙ cos 2 α = sin 2 α. Приложете формулата 1) и след това формулата 2) .
Помня: tgα ∙ cosα = гряхα.
По същия начин, използвайки формулата 3) на разположение: ctgα ∙ гряхα = cosα. Помня!
з) ctg 2 αcos 2 α – ctg 2 α = ctg 2 α(cos 2 α – 1) = ctg 2 α ∙ (-sin 2 α) = -cos 2 α.
И) cos 2 α+tg 2 αcos 2 α = cos 2 α(1+tg 2 α) = 1. Първо извадихме общия множител от скобите и опростихме съдържанието на скобите, използвайки формулата 7).
Преобразуване на израз:

Приложихме формулата 7) и получи произведението на сумата от два израза от непълния квадрат на разликата на тези изрази - формулата за сбора на кубовете на два израза:
a 3 + b 3 = (a + b)(a 2 – ab + b 2). Ние имаме А = 1, b= tan 2 α.
Опростете:

Страница 1 от 1 1