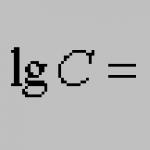Статистическа и класическа дефиниция на вероятностното свойство на вероятността. Статистическа дефиниция на вероятността

Основни понятия. Теореми за събиране и умножение.

Формули на пълната вероятност, Бейс, Бернули. Теореми на Лаплас.

Въпроси

1. Предмет на теорията на вероятностите.
2. Видове събития.
3. Класическа дефиниция на вероятността.
4. Статистическа дефиниция на вероятността.
5. Геометрично определение на вероятността.
6. Теорема за събиране на вероятностите за несъвместими събития.
7. Теорема за умножаване на вероятностите за независими събития.
8. Условна вероятност.
9. Умножаване на зависими събития.
10. Добавяне на съвместни събития.
11. Формула за пълна вероятност.
12. Формула на Бейс.

13. Бином, полиномен закон на разпределение.

1. Предмет на теорията на вероятностите. Основни понятия.

Събитие в теорията на вероятностите е всеки факт, който може да възникне в резултат на някакъв опит (тест).

Например:Стрелецът стреля в целта. Изстрелът е изпитание, попадението в целта е събитие. Събитията обикновено се обозначават

Едно-единствено случайно събитие е следствие от множество случайни причини, които много често не могат да бъдат отчетени. Ако обаче разгледаме масови хомогенни събития (наблюдавани много пъти по време на експеримента при едни и същи условия), тогава те се оказват обект на определени модели: ако хвърлите монета при едни и същи условия голям брой пъти, можете да предвидите с малка грешка, че броят на срещанията на герба ще бъде равен на половината от броя на хвърлянията.

Предмет на теорията на вероятностите е изследването на вероятностните модели на масови хомогенни случайни събития. Методите на теорията на вероятностите се използват широко в теориите за надеждност, стрелба, автоматично управление и др. Теорията на вероятностите служи за основа на математическата и приложна статистика, която от своя страна се използва при планирането и организирането на производството, при анализа на технологичните процеси и др.

Дефиниции.

1. Ако в резултат на преживяното събитието

а) винаги ще се случи, тогава това е надеждно събитие,

б) никога няма да се случи, тогава - невъзможно събитие,

в) може да се случи, може и да не се случи, тогава е случайно (възможно) събитие.

2. Събитията се наричат ​​еднакво вероятни, ако има причина да се смята, че никое от тези събития няма по-голям шанс да се случи в резултат на опит от други.

3. Събитията и са съвместни (несъвместими), ако настъпването на едно от тях не изключва (изключва) настъпването на другото.

4. Група от събития е съвместима, ако поне две събития от тази група са съвместими, в противен случай тя е несъвместима.

5. Група от събития се нарича пълна, ако едно от тях определено ще се случи в резултат на преживяването.

Пример 1.Произвеждат се три изстрела по мишената: Let - уцелване (пропускане) на първия изстрел - на втория изстрел - на третия изстрел. Тогава

а) - обща група от еднакво възможни събития.

б) - пълна група от несъвместими събития. - събитие, което е обратното.

в) - пълна група от събития.

Класическа и статистическа вероятност

Класическият метод за определяне на вероятността се използва за пълна група от еднакво възможни несъвместими събития.

Всяко събитие в тази група ще се нарича случай или елементарен резултат. Във връзка с всяко събитие случаите се разделят на благоприятни и неблагоприятни.

Определение 2.Вероятността за събитие е количеството

където е броят на случаите, благоприятни за настъпване на събитието, е общият брой еднакво възможни случаи в даден експеримент.

Пример 2.Хвърлят се два зара. Нека събитието - сумата от изпуснатите точки е равно на . Намирам .

а) Грешно решение. Има само 2 възможни случая: и - пълна група от несъвместими събития. Само един случай е благоприятен, т.е.

Това е грешка, тъй като те не са еднакво възможни.

б) Общо еднакво възможни случаи. Благоприятни случаи: пролапс

Слабостите на класическата дефиниция са:

1. - броят на случаите е краен.

2. Резултатът от експеримент много често не може да бъде представен под формата на набор от елементарни събития (случаи).

3. Трудно е да се посочат причините случаите да се считат за еднакво възможни.

Нека се проведат поредица от тестове.

Определение 3.Относителната честота на събитието е количеството

където е броят опити, в които са се появили събития и е общият брой опити.

Дългосрочните наблюдения показват, че в различни експерименти при достатъчно големи

Тя се променя малко, варирайки около някакво постоянно число, което наричаме статистическа вероятност.

Вероятността има следните свойства:

Алгебра на събитията

7.3.1 Дефиниции.

8. Сборът или обединението на няколко събития е събитие, състоящо се от поне едно от тях.

9. Продуктът от няколко събития е събитие, състоящо се от съвместното възникване на всички тези събития.

От пример 1. - поне едно попадение с три изстрела, - попадение с първи и втори изстрел и пропуск с трето.

Точно едно попадение.

Поне две попадения.

10. Две събития се наричат ​​независими (зависими), ако вероятността за едно от тях не зависи (зависи) от настъпването или ненастъпването на другото.

11. Няколко събития се наричат ​​колективно независими, ако всяко от тях и всяка линейна комбинация от останалите събития са независими събития.

12. Условна вероятност е вероятността за събитие, изчислена при предположението, че събитието се е случило.

7.3.2 Теорема за умножение на вероятностите.

Вероятността за съвместно възникване (производство) на няколко събития е равна на произведението на вероятността за едно от тях от условните вероятности на останалите събития, изчислени при допускането, че всички предишни събития са се случили

Следствие 1.Ако - са съвместно независими, тогава

Наистина: от .

Пример 3.В урната има 5 бели, 4 черни и 3 сини топки. Всеки тест се състои от теглене на една топка на случаен принцип от урна. Каква е вероятността при първия опит да се появи бяла топка, при втория – черна топка, при третия – синя топка, ако

а) всеки път, когато топката се върне в урната.

- в урната след първия тест на топките 4 от тях са бели. . Оттук

б) топката не се връща в урната. След това - независими в съвкупност и

7.3.3 Теорема за добавяне на вероятности.

Вероятността поне едно от събитията да се случи е равна на

Следствие 2.Ако събитията са по двойки несъвместими, тогава

Наистина в този случай

Пример 4.Произвеждат се три изстрела по една мишена. Вероятността за попадение при първия изстрел е , при втория - , при третия - . Намерете вероятността за поне едно попадение.

Решение.Нека има попадение на първия изстрел, на втория, на третия и поне едно попадение на три изстрела. Тогава къде са съвместно независимите в съвкупността. Тогава

Следствие 3.Ако по двойки несъвместими събития образуват пълна група, тогава

Следствие 4.За противоположни събития

Понякога при решаване на проблеми е по-лесно да се намери вероятността за обратното събитие. Например в пример 4 - пропуск с три изстрела. Тъй като независими в съвкупност, а след това

Случайността на възникване на събития е свързана с невъзможността да се предвиди предварително резултатът от конкретен тест. Ако обаче разгледаме, например, тест: многократно хвърляне на монета, ω 1, ω 2, ..., ω n, тогава се оказва, че в приблизително половината от резултатите ( н / 2) открит е определен модел, който съответства на концепцията за вероятност.

Под вероятностсъбития Асе разбира като определена числена характеристика на възможността за настъпване на събитие А. Нека обозначим тази цифрова характеристика Р(А). Има няколко подхода за определяне на вероятността. Основните са статистически, класически и геометрични.

Нека се произвежда нтестове и в същото време някакво събитие Апристигна н A пъти. Номер нА се нарича абсолютна честота(или просто честотата) на събитието А, а релацията се нарича относителна честота на възникване на събитие А.Относителна честота на всяко събитие характеризиращ се със следните свойства:

Основата за прилагане на методите на теорията на вероятностите за изследване на реални процеси е обективното съществуване на случайни събития, които имат свойството на честотна стабилност. Множество изпитания на изследваното събитие Апокажете това на свобода нотносителна честота ( А) остава приблизително постоянен.

Статистическата дефиниция на вероятността е, че вероятността за събитие А се приема за постоянна стойност p(A), около която стойностите на относителните честоти варират (А) с неограничено увеличаване на броя на тестоветен.

Бележка 1. Обърнете внимание, че границите на промяна на вероятността за случайно събитие от нула до единица са избрани от Б. Паскал за удобство на неговото изчисляване и приложение. В кореспонденция с П. Ферма Паскал посочи, че всеки интервал може да бъде избран като посочен интервал, например от нула до сто и други интервали. В проблемите по-долу в това ръководство вероятностите понякога се изразяват като проценти, т.е. от нула до сто. В този случай процентите, дадени в задачите, трябва да се превърнат в дялове, т.е. дели на 100.

Пример 1.Проведени са 10 серии хвърляния на монети, всяка с 1000 хвърляния. величина ( А) във всяка от сериите е равно на 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500; 0,497; 0,494; 0,484. Тези честоти са групирани около Р(А) = 0,5.

Този пример потвърждава, че относителната честота ( А) е приблизително равен Р(А), т.е.

Понятието вероятност за събитие се отнася до основните понятия на теорията на вероятностите. Вероятността е количествена мярка за възможността за възникване на случайно събитие A. Означава се с P(A) и има следните свойства.

Вероятността е положително число, вариращо от нула до едно:

Вероятността за невъзможно събитие е нула

Вероятността за надеждно събитие е равна на единица

Класическа дефиниция на вероятността. Нека = (1, 2,…, n) е пространството от елементарни събития, които описват всички възможни елементарни резултати и образуват пълна група от несъвместими и еднакво възможни събития. Нека събитие A съответства на подмножество от m елементарни резултата

тези резултати се наричат ​​благоприятни за събитие А. В класическата дефиниция на вероятността се смята, че вероятността от всеки елементарен резултат

и вероятността за събитие А, благоприятствано от m резултата, е равна на

Оттук и определението:

Вероятността за събитие А е отношението на броя на резултатите, благоприятни за това събитие, към общия брой на всички еднакво възможни несъвместими елементарни резултати, които образуват пълната група. Вероятността се дава от формулата

където m е броят на елементарните резултати, благоприятни за събитие А, и е броят на всички възможни елементарни резултати на теста.

Класическата дефиниция на вероятността дава възможност в някои задачи да се изчисли аналитично вероятността за събитие.

Нека се проведе експеримент, в резултат на който могат да се случат определени събития. Ако тези събития образуват пълна група от по двойки несъвместими и еднакво възможни събития, тогава се казва, че опитът има симетрия на възможните резултати и се свежда до „схема от случаи“. За експерименти, които са сведени до схема на случай, е приложима класическата вероятностна формула.

Пример 1.13. Лотарията тегли 1000 билета, включително 5 печеливши. Определете вероятността при закупуване на един билет за лотария да получите печалба

Елементарното събитие от това преживяване е закупуването на билет. Всеки лотариен билет е уникален, тъй като има собствен номер, а закупеният билет не се връща. Събитие А е, че печелившият билет е закупен. При закупуване на един от 1000 билета, всички възможни резултати от това преживяване ще бъдат = 1000, резултатите образуват пълна група от несъвместими събития. Броят на резултатите, благоприятни за събитие А, ще бъде равен на =5. Тогава вероятността да спечелите чрез закупуване на един билет е равна на

P(A) = = 0,005

За директно изчисляване на вероятностите е удобно да се използват комбинаторни формули. Нека демонстрираме това, като използваме примера на проблем с контрола на пробите.

Пример 1.14 Нека има партида продукти, някои от които са дефектни. Част от продуктите се избират за контрол. Каква е вероятността сред избраните продукти да има точно дефектни?

Елементарното събитие в този експеримент е изборът на елементарно подмножество от оригиналното елементарно множество. Изборът на всяка част от продукти от партида продукти може да се счита за еднакво възможни събития, така че този опит се свежда до схема от случаи. За да изчислите вероятността на събитието A = (сред дефектни продукти, ако са избрани от партида дефектни продукти), можете да приложите класическата вероятностна формула. Броят на всички възможни резултати от експеримента е броят на начините, по които продуктите могат да бъдат избрани от партида, той е равен на броя на комбинациите от елементи по: . Събитие, благоприятно за събитие А, се състои от произведението на две елементарни събития: (от дефектни продукти _ са избрани (от _ стандартни продукти _ са избрани). Броят на такива събития, в съответствие с правилото за умножение на комбинаториката, ще бъде

Тогава желаната вероятност

Например нека =100, =10, =10, =1. Тогава вероятността сред избраните 10 продукта да има точно един дефектен продукт е равна на

Статистическа дефиниция на вероятността. За да се приложи класическата дефиниция на вероятността в условията на даден експеримент, е необходимо експериментът да съответства на модела от случаи, а за повечето реални проблеми тези изисквания е практически невъзможно да бъдат изпълнени. Вероятността от събитие обаче е обективна реалност, която съществува независимо от това дали класическата дефиниция е приложима или не. Има нужда от друго определение на вероятността, приложимо, когато опитът не съответства на модела на случаите.

Нека експериментът се състои от провеждане на серия от тестове, повтарящи един и същ експеримент, и нека събитие А се случи веднъж в серия от експерименти. Относителната честота на събитието W(A) е съотношението на броя на експериментите, в които е настъпило събитие А, към броя на всички проведени експерименти

Експериментално е доказано, че честотата има свойството на стабилност: ако броят на експериментите в серия е достатъчно голям, тогава относителните честоти на събитие А в различни серии от един и същ експеримент се различават малко една от друга.

Статистическата вероятност за събитие е числото, към което клонят относителните честоти, ако броят на експериментите нараства неограничено.

За разлика от класическата априорна (изчислена преди експеримента) вероятност, статистическата вероятност е апостериорна (получена след експеримента).

Пример 1.15 Метеорологичните наблюдения в продължение на 10 години в определен район показват, че броят на дъждовните дни през юли през различните години е: 2; 4; 3; 2; 4; 3; 2; 3; 5; 3. Определете вероятността всеки конкретен ден през юли да бъде дъждовен

Събитие А е, че ще вали в определен ден от юли, например 10 юли. Предоставената статистика не съдържа информация кои конкретни дни през юли е валяло, така че можем да приемем, че всички дни са еднакво възможни за това събитие. Нека една година е една поредица от тестове от 31 еднодневни. Сериите са общо 10. Относителната честота на серията е:

Честотите са различни, но се наблюдава групиране около числото 0,1. Това число може да се приеме като вероятност за събитие А. Ако вземем всички дни от юли за десет години като една серия от тестове, тогава статистическата вероятност за събитие А ще бъде равна на

Геометрично определение на вероятността. Тази дефиниция на вероятността обобщава класическата дефиниция за случая, когато пространството от елементарни резултати включва неизброимо множество от елементарни събития и възникването на всяко от събитията е еднакво възможно. Геометричната вероятност за събитие А е съотношението на мярката (А) на региона, благоприятен за настъпване на събитието, към мярката () на целия регион

Ако площите представляват а) дължини на сегменти, б) площи на фигури, в) обеми на пространствени фигури, тогава геометричните вероятности са съответно равни

Пример 1.16. Рекламите са разлепени на интервали от 10 метра по протежение на търговския ред. Някои клиенти имат ширина на видимост от 3 метра. Каква е вероятността той да не забележи рекламата, ако се движи перпендикулярно на търговския ред и може да пресече реда във всяка точка?

Участъкът от търговския ред, разположен между две реклами, може да бъде представен като прав сегмент AB (фиг. 1.6). След това, за да забележи купувачът рекламите, той трябва да премине през прави отсечки AC или DV, равни на 3 m. Ако пресече търговския ред в една от точките на сегмента SD, чиято дължина е 4 m, тогава той няма да забележи рекламата. Вероятността за това събитие ще бъде

Теория на вероятностите – математическа наука, която изучава закономерностите на случайните явления. Случайните явления се разбират като явления с несигурен резултат, които възникват, когато определен набор от условия се възпроизвежда многократно.

Например, когато хвърляте монета, не можете да предвидите на коя страна ще падне. Резултатът от хвърлянето на монета е случаен. Но при достатъчно голям брой хвърляния на монети има определен модел (гербът и знакът за решетка ще изпаднат приблизително еднакъв брой пъти).

Основни понятия на теорията на вероятностите

Тест (опит, експеримент) - прилагането на определен набор от условия, при които се наблюдава това или онова явление и се записва този или онзи резултат.

Например: хвърляне на зар и получаване на брой точки; температурна разлика на въздуха; метод за лечение на заболяването; някакъв период от живота на човек.

Случайно събитие (или просто събитие) – резултат от теста.

Примери за случайни събития:

получаване на една точка при хвърляне на зар;

обостряне на коронарна болест на сърцето с рязко повишаване на температурата на въздуха през лятото;

развитие на усложнения на заболяването поради неправилен избор на метод на лечение;

прием в университет след успешно обучение в училище.

Събитията се обозначават с главни букви на латинската азбука: А , б , ° С , …

Събитието се нарича надежден , ако в резултат на теста непременно трябва да възникне.

Събитието се нарича невъзможен , ако в резултат на теста изобщо не може да възникне.

Например, ако всички продукти в една партида са стандартни, тогава извличането на стандартен продукт от нея е надеждно събитие, но извличането на дефектен продукт при същите условия е невъзможно събитие.

КЛАСИЧЕСКА ДЕФИНИЦИЯ НА ВЕРОЯТНОСТТА

Вероятността е едно от основните понятия на теорията на вероятностите.

Класическа вероятност за събитие се нарича съотношение на броя на благоприятните за събитието случаи , към общия брой дела, т.е.

, (5.1)

Където
- вероятност за събитие ,

- брой случаи, благоприятни за събитието ,

- общ брой случаи.

Свойства на вероятността за събитие

Вероятността за всяко събитие е между нула и едно, т.е.

Вероятността за надеждно събитие е равна на единица, т.е.

.

Вероятността за невъзможно събитие е нула, т.е.

.

(Предложете устно решаване на няколко прости задачи).

СТАТИСТИЧЕСКО ОПРЕДЕЛЯНЕ НА ВЕРОЯТНОСТТА

На практика оценяването на вероятностите за събития често се основава на това колко често ще се случи дадено събитие в извършените тестове. В този случай се използва статистическата дефиниция на вероятността.

Статистическа вероятност за събитие наречена граница на относителната честота (отношението на броя на случаите м, благоприятни за настъпване на събитие , към общия брой проведени тестове), когато броят на тестовете клони към безкрайност, т.е.

Където
- статистическа вероятност за събитие ,
- брой опити, в които се появи събитието , - общ брой тестове.

За разлика от класическата вероятност, статистическата вероятност е характеристика на експерименталната вероятност. Класическата вероятност служи за теоретично изчисляване на вероятността от дадено събитие при дадени условия и не изисква извършването на тестове в действителност. Статистическата вероятностна формула се използва за експериментално определяне на вероятността от събитие, т.е. предполага се, че тестовете действително са извършени.

Статистическата вероятност е приблизително равна на относителната честота на случайно събитие, следователно на практика относителната честота се приема като статистическа вероятност, т.к. статистическата вероятност е практически невъзможно да се намери.

Статистическата дефиниция на вероятността е приложима за случайни събития, които имат следните свойства:

Теореми за събиране и умножение на вероятностите

Основни понятия

а) Единствените възможни събития

събития
Те се наричат ​​единствените възможни, ако в резултат на всеки тест поне един от тях със сигурност ще се случи.

Тези събития образуват пълна група от събития.

Например, когато хвърляте зар, единствените възможни събития са страните с една, две, три, четири, пет и шест точки. Те образуват пълна група от събития.

б) Събитията се наричат ​​несъвместими, ако настъпването на едно от тях изключва настъпването на други събития в същото изпитване. В противен случай те се наричат ​​съвместни.

в) Обратноназовете две уникално възможни събития, които образуват пълна група. Определете И .

Ж) Събитията се наричат ​​независими, ако вероятността за възникване на един от тях не зависи от извършването или неизпълнението на други.

Действия върху събития

Сумата от няколко събития е събитие, състоящо се от настъпването на поне едно от тези събития.

Ако И – съвместни събития, след това тяхната сума
или
обозначава настъпването или на събитие А, или на събитие Б, или на двете събития заедно.

Ако И – несъвместими събития, след това тяхната сума
означава събитие или събития , или събития .

Количество събития означават:

Продуктът (пресечната точка) на няколко събития е събитие, състоящо се от съвместното възникване на всички тези събития.

Произведението на две събития се означава с
или
.

работа събития представляват

Теорема за събиране на вероятности за несъвместими събития

Вероятността за сумата от две или повече несъвместими събития е равна на сумата от вероятностите за тези събития:

За две събития;

- За събития.

Последствия:

а) Сума от вероятностите за противоположни събития И равно на едно:

Вероятността за обратното събитие се означава с :
.

б) Сума от вероятности от събития, образуващи пълна група от събития, е равно на едно: или
.

Теорема за добавяне на вероятности за съвместни събития

Вероятността за сумата от две съвместни събития е равна на сумата от вероятностите за тези събития без вероятностите за тяхното пресичане, т.е.

Теорема за умножение на вероятностите

а) За две независими събития:

б) За две зависими събития

Където
– условна вероятност за събитие , т.е. вероятност за събитие , изчислено при условие, че събитието се случи.

в) За независими събития:

.

г) Вероятност за настъпване на поне едно от събитията , образувайки пълна група от независими събития:

Условна вероятност

Вероятност за събитие , изчислено при допускане, че събитието се е случило , се нарича условна вероятност на събитието и е обозначен
или
.

При изчисляване на условната вероятност с помощта на класическата вероятностна формула, броят на резултатите И
изчислено, като се вземе предвид фактът, че преди да настъпи събитието настъпи събитие .

За да се сравнят количествено събитията едно с друго според степента на тяхната възможност, очевидно е необходимо да се свърже определено число с всяко събитие, което е толкова по-голямо, колкото по-вероятно е събитието. Ще наречем това число вероятност за събитие. По този начин, вероятност за събитиее числена мярка за степента на обективна възможност за това събитие.

Първото определение на вероятността трябва да се счита за класическото, което произлиза от анализа на хазарта и първоначално се прилага интуитивно.

Класическият метод за определяне на вероятността се основава на концепцията за еднакво възможни и несъвместими събития, които са резултат от дадено преживяване и образуват пълна група от несъвместими събития.

Най-простият пример за еднакво възможни и несъвместими събития, образуващи пълна група, е появата на една или друга топка от урна, съдържаща няколко топки с еднакъв размер, тегло и други осезаеми характеристики, различаващи се само по цвят, старателно смесени преди да бъдат извадени.

Следователно, тест, чиито резултати формират пълна група от несъвместими и еднакво възможни събития, се казва, че може да бъде сведен до модел от урни или модел от случаи, или се вписва в класическия модел.

Еднакво възможни и несъвместими събития, които съставляват пълна група, ще се наричат ​​просто случаи или шансове. Освен това във всеки експеримент, наред със случаите, могат да възникнат и по-сложни събития.

Пример: При хвърляне на зарове, заедно със случаите A i - загуба на i-точки от горната страна, можем да разгледаме такива събития като B - загуба на четен брой точки, C - загуба на няколко точки, кратни на три...

Във връзка с всяко събитие, което може да се случи по време на експеримента, случаите се разделят на благоприятен, при които това събитие настъпва, и неблагоприятни, при които събитието не настъпва. В предишния пример събитие B е предпочитано от случаи A 2, A 4, A 6; събитие C - случаи A 3, A 6.

Класическа вероятностнастъпването на определено събитие се нарича съотношението на броя на случаите, благоприятни за настъпването на това събитие, към общия брой еднакво възможни, несъвместими случаи, които съставляват пълната група в даден експеримент:

Където P(A)- вероятност за настъпване на събитие А; м- броят на случаите, благоприятни за събитие А; н- общ брой случаи.

Примери:

1) (вижте примера по-горе) P(B)= , P(C) =.

2) Урната съдържа 9 червени и 6 сини топки. Намерете вероятността една или две произволно изтеглени топки да се окажат червени.

А- червена топка, изтеглена на случаен принцип:

м= 9, н= 9 + 6 = 15, P(A)=

б- две произволно изтеглени червени топки:

Следните свойства следват от класическата дефиниция на вероятността (покажете себе си):

1) Вероятността за невъзможно събитие е 0;

2) Вероятността за надеждно събитие е 1;

3) Вероятността за всяко събитие е между 0 и 1;

4) Вероятността за събитие, противоположно на събитие А,

Класическата дефиниция на вероятността предполага, че броят на резултатите от едно изпитание е краен. В практиката много често има тестове, чийто брой възможни случаи е безкраен. В допълнение, слабостта на класическата дефиниция е, че много често е невъзможно да се представи резултатът от теста под формата на набор от елементарни събития. Още по-трудно е да се посочат причините елементарните резултати от теста да се считат за еднакво възможни. Обикновено равнопоставеността на резултатите от елементарния тест се заключава от съображения за симетрия. Такива задачи обаче са много редки на практика. Поради тези причини, наред с класическата дефиниция за вероятност се използват и други дефиниции за вероятност.

Статистическа вероятностсъбитие A е относителната честота на възникване на това събитие в извършените тестове:

където е вероятността за възникване на събитие А;

Относителна честота на поява на събитие А;

Броят опити, в които се появи събитие А;

Общ брой опити.

За разлика от класическата вероятност, статистическата вероятност е експериментална характеристика.

Пример: За контрол на качеството на продуктите от партида са избрани на случаен принцип 100 продукта, сред които 3 продукта са се оказали дефектни. Определете вероятността от брак.

Статистическият метод за определяне на вероятността е приложим само за онези събития, които имат следните свойства:

Разглежданите събития трябва да бъдат резултатите само от тези тестове, които могат да бъдат възпроизведени неограничен брой пъти при един и същи набор от условия.

Събитията трябва да имат статистическа стабилност (или стабилност на относителните честоти). Това означава, че в различни серии от тестове относителната честота на събитието се променя малко.

Броят на опитите, водещи до събитие А, трябва да е доста голям.

Лесно е да се провери, че свойствата на вероятността, произтичащи от класическата дефиниция, се запазват и в статистическата дефиниция на вероятността.