В какво се състои интегрирането по части? Основни методи за интегриране

>>Методи на интегриране

Основни методи за интегриране

Дефиниция на интеграл, определен и неопределен интеграл, таблица на интегралите, формула на Нютон-Лайбниц, интегриране по части, примери за изчисляване на интеграли.

Неопределен интеграл

Извиква се функция F(x), диференцируема в даден интервал X първоизводна на функцията f(x) или интеграла на f(x), ако за всяко x ∈X е валидно следното равенство:

F " (x) = f(x). (8.1)

Намирането на всички първоизводни за дадена функция се нарича нейна интеграция. Неопределена интегрална функция f(x) на даден интервал X е множеството от всички първообразни функции за функцията f(x); обозначаване -

Ако F(x) е някакво първообразно на функцията f(x), тогава ∫ f(x)dx = F(x) + C, (8.2)

където C е произволна константа.

Таблица на интегралите

Директно от дефиницията получаваме основните свойства на неопределения интеграл и списък от таблични интеграли:

1) d∫f(x)dx=f(x)

2) ∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Списък на табличните интеграли

1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sin x + C

7. = арктан x + C

8. = arcsin x + C

10. = - ctg x + C

Замяна на променливи

За да интегрирате много функции, използвайте метода за заместване на променливи или замествания,което ви позволява да намалите интегралите до таблична форма.

Ако функцията f(z) е непрекъсната върху [α,β], функцията z =g(x) има непрекъсната производна и α ≤ g(x) ≤ β, тогава

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

Освен това, след интегриране от дясната страна, трябва да се направи заместването z=g(x).

За да го докажете, достатъчно е да напишете оригиналния интеграл във формата:

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Например:

2) .

Метод на интегриране по части

Нека u = f(x) и v = g(x) са функции, които имат непрекъснато . Тогава, според работата,

d(uv))= udv + vdu или udv = d(uv) - vdu.

За израза d(uv) антипроизводното очевидно ще бъде uv, така че формулата е валидна:

∫ udv = uv - ∫ vdu (8.4.)

Тази формула изразява правилото интеграция по части. Това води интегрирането на израза udv=uv"dx до интегрирането на израза vdu=vu"dx.

Нека, например, искате да намерите ∫xcosx dx. Нека поставим u = x, dv = cosxdx, така че du=dx, v=sinx. Тогава

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

Правилото за интегриране по части има по-ограничен обхват от заместването на променливи. Но има цели класове интеграли, напр.

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и други, които се изчисляват точно с помощта на интегриране по части.

Определен интеграл

Концепцията за определен интеграл се въвежда по следния начин. Нека функция f(x) е дефинирана на интервал. Нека разделим сегмента [a,b] на нчасти по точки a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i = x i - x i-1. Извиква се сума от формата f(ξ i)Δ x i интегрална сума, а неговата граница при λ = maxΔx i → 0, ако съществува и е крайна, се нарича определен интегралфункции f(x) на апреди bи се обозначава:

F(ξ i)Δx i (8.5).

Функцията f(x) в този случай се извиква интегрируеми на интервала, се наричат числата a и b долна и горна граница на интеграла.

Следните свойства са верни за определен интеграл:

4), (k = const, k∈R);

7) f(ξ)(b-a) (ξ∈).

Последното свойство се нарича теорема за средната стойност.

Нека f(x) е непрекъснато върху . Тогава на този сегмент има неопределен интеграл

∫f(x)dx = F(x) + C

и се провежда Формула на Нютон-Лайбниц, свързващ определения интеграл с неопределения интеграл:

F(b) - F(a). (8,6)

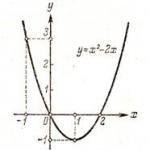
Геометрична интерпретация: определеният интеграл е площта на криволинеен трапец, ограничен отгоре от кривата y=f(x), прави x = a и x = b и сегмент от оста вол.

Неправилни интеграли

Интеграли с безкрайни граници и интеграли на прекъснати (неограничени) функции се наричат не твоя собствена. Неправилни интеграли от първи род -Това са интеграли върху безкраен интервал, дефиниран както следва:

(8.7)

Ако тази граница съществува и е крайна, тогава тя се нарича конвергентен неправилен интеграл на f(x)на интервала [a,+ ∞), и се извиква функцията f(x). интегрируеми в безкраен интервал[a,+ ∞). В противен случай се казва, че интегралът е не съществува или се разминава.

Неправилните интеграли на интервалите (-∞,b] и (-∞, + ∞) се дефинират по подобен начин:

Нека дефинираме понятието интеграл на неограничена функция. Ако f(x) е непрекъснато за всички стойности хсегмент , с изключение на точката c, в която f(x) има безкраен прекъсване, тогава неправилен интеграл от втория вид f(x) вариращи от a до bсумата се нарича:

ако тези граници съществуват и са крайни. Обозначаване:

Примери за интегрални изчисления

Пример 3.30.Изчислете ∫dx/(x+2).

Решение.Нека означим t = x+2, тогава dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.

Пример 3.31. Намерете ∫ tgxdx.

Решение.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Нека t=cosx, тогава ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Пример3.32 . Намерете ∫dx/sinx

Решение.

Пример3.33. Намирам .

Решение. =

Пример3.34 . Намерете ∫arctgxdx.

Решение. Нека интегрираме по части. Нека означим u=arctgx, dv=dx. Тогава du = dx/(x 2 +1), v=x, откъдето ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; защото
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Пример3.35 . Изчислете ∫lnxdx.

Решение.Прилагайки формулата за интегриране по части, получаваме:
u=lnx, dv=dx, du=1/x dx, v=x. Тогава ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Пример3.36 . Изчислете ∫e x sinxdx.

Решение.Нека означим u = e x, dv = sinxdx, тогава du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Също така интегрираме интеграла ∫e x cosxdx по части: u = e x, dv = cosxdx, du=e x dx, v=sinx. Ние имаме:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Получихме отношението ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, от което 2∫e x sinx dx = - e x cosx + e x sinx + C.

Пример 3.37. Изчислете J = ∫cos(lnx)dx/x.

Решение.Тъй като dx/x = dlnx, тогава J= ∫cos(lnx)d(lnx). Заменяйки lnx с t, стигаме до интеграла на таблицата J = ∫ costdt = sint + C = sin(lnx) + C.

Пример 3.38 . Изчислете J = .

Решение.Като се има предвид, че = d(lnx), заместваме lnx = t. Тогава J = .

Методът на интегриране по части се използва, когато е необходимо да се опрости съществуващият неопределен интеграл или да се намали до таблична стойност. Най-често се използва при наличието на експоненциални, логаритмични, директни и обратни тригонометрични формули и техните комбинации в интегранта.

Основната формула, необходима за използване на този метод, е:

∫ f (x) d x = ∫ u (x) d (v (x)) = u (x) v (x) - ∫ v (x) d (u (x))

Това означава, че първо трябва да представим израза под интеграла като произведение на функцията u (x) и диференциала на функцията v (x). След това изчисляваме стойността на функцията v (x) по някакъв метод (най-често се използва методът на директно интегриране) и заместваме получените изрази в посочената формула, намалявайки първоначалния интеграл до разликата u (x) v (x) - ∫ v (x) d(u(x)) . Полученият интеграл също може да бъде взет с помощта на всеки метод на интегриране.

Нека разгледаме задача, в която трябва да намерим множеството от първоизводни на функцията логаритъм.

Пример 1

Изчислете неопределения интеграл ∫ ln (x) d x.

Решение

Използваме метода на интегриране по части. За да направим това, вземаме ln (x) като функция на u (x) и остатъка от интегранта като d (v (x)). В резултат на това получаваме, че ln (x) d x = u (x) d (v (x)), където u (x) = ln (x), d (v (x)) = d x.

Диференциалът на функцията u(x) е d(u(x)) - u"(x)d x = d x x, а функцията v(x) може да бъде записана като v(x) = ∫ d(v(x) ) = ∫ d x = x

Важно:константата C ще се счита за равна на 0 при изчисляване на функцията v (x).

Нека заместим полученото във формулата за интегриране по части:

∫ ln (x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = ln (x) x - ∫ x d x x = ln (x) x - ∫ d x = ln ( x) x - x + C 1 = = x (ln (x) - 1) + C

където C = - C 1

Отговор:∫ ln (x) d x = x (ln (x) - 1) + C .

Най-трудното при прилагането на този метод е да изберете коя част от оригиналния израз под интеграла да приемете като u (x) и коя като d (v (x)).

Нека да разгледаме няколко стандартни случая.

Ако нашето условие съдържа интеграли от вида ∫ P n (x) · e a x d x , ∫ P n (x) · sin (a x) d x или ∫ P n (x) · cos (a x) d x , където a е коефициент и P n (x) е полином от степен n, тогава P n (x) трябва да се приеме като функция u (x).

Пример 2

Намерете множеството от първопроизводни на функцията f (x) = (x + 1) · sin (2 x) .

Решение

Можем да вземем неопределения интеграл ∫ (x + 1) · sin (2 x) d x на части. Взимаме x + 1 като u (x) и sin (2 x) d x като d (v (x)), тоест d (u (x)) = d (x + 1) = d x.

Използвайки директно интегриране, получаваме:

v (x) = ∫ sin (2 x) d x = - 1 2 cos (2 x)

Заместете във формулата за интегриране по части:

∫ (x + 1) sin (2 x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = (x + 1) - 1 2 cos (2 x ) - ∫ - 1 2 cos (2 x) d x = = - 1 2 (x + 1) cos (2 x) + 1 2 ∫ cos (2 x) d (x) = = - 1 2 (x + 1) cos ( 2 x) + 1 4 sin (2 x) + C

Отговор:∫ (x + 1) · sin (2 x) d x = - 1 2 (x + 1) · cos (2 x) + 1 4 sin (2 x) + C .

Пример 3

Изчислете неопределения интеграл ∫ (x 2 + 2 x) e x d x.

Решение

Взимаме полином от втори ред x 2 + 2 x като u (x) и d (v (x)) - e x d x .

∫ x 2 + 2 x e x d x = u (x) = x 2 + 2 x , d (v (x)) = e x d x d (u (x)) = (2 x + 2) d x , v (x) = ∫ e x d x = e x = = u (x) v (x) - ∫ v (x) d (u (x)) = (x 2 + 2 x) e x - ∫ (2 x + 2) e x d x

Към това, което получихме, трябва отново да приложим метода на интегриране по части:

∫ (2 x + 2) e x d x = (x 2 + 2 x) e x - ∫ 2 x + 2 e x d x = = u (x) = (2 x + 2) , d (v (x)) = e x d x d (u ( x)) = 2 d x , v (x) = ∫ e x d x = e x = = (x 2 + 2 x) e x - (2 x + 2) e x - ∫ v (x) d (u (x)) = = ( x 2 + 2 x) e x - (2 x + 2) e x - ∫ 2 e x d x = = (x 2 + 2 x - 2 x - 2) e x + 2 ∫ e x d x = (x 2 - 2) e x + 2 e x + C = x 2 e x + C

Отговор:∫ (x 2 + 2 x) e x d x = x 2 e x + C .

Пример 4

Изчислете интеграла ∫ x 3 cos 1 3 x d x .

Решение

Според метода на интегриране по части приемаме u (x) = x 3 и d (v (x)) = cos 1 3 x d x.

В този случай d (u (x)) = 3 x 2 d x и v (x) = ∫ cos 1 3 x d x = 3 sin 1 3 x .

Сега нека заместим получените изрази във формулата:

∫ x 3 cos 1 3 x d x = u (x) v (x) - ∫ v (x) d (u)) = = x 3 3 sin 1 3 x - ∫ 3 x 2 3 sin 1 3 x d x = = 3 x 3 sin 1 3 x - 9 ∫ x 2 sin 1 3 x d x

Имаме неопределен интеграл, който отново трябва да се вземе на части:

∫ x 3 cos 1 3 x d x = 3 x 3 sin 1 3 x - 9 ∫ x 2 sin 1 3 x d x = = u (x) = x 2 , d (v (x)) = sin 1 3 x d x d (u (x) )) = 2 x d x , v (x) = ∫ sin 1 3 x d x = - 3 cos 1 3 x = = 3 x 3 sin 1 3 x - 9 - 3 x 2 cos 1 3 x - ∫ - 3 cos 1 3 x · 2 x d x = = 3 x 3 sin 1 3 x + 27 x 2 · cos 1 3 x - 54 ∫ x cos 1 3 x d x

Отново извършваме частично интегриране:

∫ x 3 cos 1 3 x d x = 3 x 3 sin 1 3 x + 27 x 2 · cos 1 3 x - 54 ∫ x cos 1 3 x d x = = u (x) = x , d (v (x)) = cos 1 3 x d x d (u (x)) = d x , v (x) = ∫ cos 1 3 x d x = 3 sin 1 3 x = = 3 x 3 sin 1 3 x + 27 x 2 cos 1 3 x - 54 3 x sin 1 3 x - ∫ 3 sin 1 3 x d x = = 3 x 3 - 162 x sin 1 3 x + 27 x 2 cos 1 3 x + 162 ∫ sin 1 3 x d x = = (3 x 3 - 162 x) sin 1 3 x + 27 x 2 cos 1 3 x - 486 cos 1 3 x + C = = (3 x 3 - 162 x) sin 1 3 x + (27 x 2 - 486) cos 1 3 x + C

Отговор:∫ x 3 cos 1 3 x d x = (3 x 3 - 162 x) sin 1 3 x + (27 x 2 - 486) cos 1 3 x + C .

Ако нашето условие съдържа интеграли от вида ∫ P n (x) · ln (a x) d x , ∫ P n (x) · a r c sin (a x) d x , ∫ P n (x) · a r c cos (a x) d x , ∫ P n (x) · a r c t g (a x) d x , ∫ P n (x) · a r c c t g (a x) d x

тогава трябва да приемем като u (x) функциите a r c t g (a x) , a r c c t g (x) , ln (a x) , a r c sin (a x) , a r cos (a x) .

Пример 5

Изчислете множеството от първоизводни на функцията (x + 1) ln (2 x) .

Решение

Вземаме ln (2 x) като u (x) и (x + 1) d x като d (v (x)). Получаваме:

d (u (x)) = (ln (2 x)) " d x = 1 2 x (2 x) " d x = d x x v (x) = ∫ (x + 1) d x = x 2 2 + x

Нека заместим тези изрази във формулата:

∫ (x + 1) ln (2 x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = x 2 2 + x ln 2 x - ∫ x 2 2 + x d x x = = x 2 2 + x ln (2 x) - ∫ x 2 + 1 d x = x 2 2 + x ln 2 x - 1 2 ∫ x d x - ∫ d x = = x 2 2 + x ln (2 x) - x 2 4 - x + C

Отговор:∫ (x + 1) ln (2 x) d x = x 2 2 + x ln (2 x) - x 2 4 - x + C .

Пример 6

Изчислете неопределения интеграл ∫ x · a r c sin (2 x) d x .

Решение

Ние решаваме коя част да приемем като u (x) и коя част да приемем като d (v (x)). Съгласно правилото, дадено по-горе, трябва да вземете r c sin (2 x) като първа функция и d (v (x)) = x d x. Получаваме:

d (u (x)) = (a r c sin (2 x) " d x = 2 x " d x 1 - (2 x) 2 = 2 d x 1 - (2 x) 2, v (x) = ∫ x d x = x 2 2

Заместете стойностите във формулата:

∫ x · a r c sin (2 x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = x 2 2 a r c sin (2 x) - ∫ x 2 2 - 2 d x 1 - (2 x) 2 = x 2 2 a r c sin (2 x) - ∫ x 2 d x 1 - 4 x 2

В резултат на това стигнахме до следното равенство:

∫ x · a r c sin (2 x) d x = x 2 2 a r c sin (2 x) - ∫ x 2 d x 1 - 4 x 2

Сега нека изчислим получения интеграл ∫ x 2 d x 1 - 4 x 2:

∫ x 2 d x 1 - 4 x 2 = ∫ x 2 d x 4 1 4 - x 2 = 1 2 ∫ x 2 d x 1 4 - x 2 = - 1 2 ∫ - x 2 d x 1 4 - x 2 = = - 1 2 ∫ 1 4 - x 2 - 1 4 1 4 - x 2 d x = - 1 2 1 4 - x 2 d x + 1 8 ∫ d x 1 4 - x 2 = = - 1 2 ∫ 1 4 - x 2 d x + 1 8 a r c sin (2 x)

Тук можете да приложите метода на интеграция по части и да получите:

∫ x 2 d x 1 - 4 x 2 = - 1 2 ∫ 1 4 - x 2 d x + 1 8 a r c sin (2 x) = = u (x) = 1 4 - x 2 , d (v (x)) = d x d (u (x)) = 1 4 - x 2 " d x 2 1 4 - x 2 = - x d x 1 4 - x 2 , v (x) = ∫ d x = x = = - 1 2 u (x) v ( x) - ∫ v (x) d (u (x)) + 1 8 a r c sin (2 x) = = - 1 2 x 1 4 - x 2 - ∫ - x 2 d x 1 4 - x 2 + 1 8 a r c sin (2 x) = = - 1 2 x 1 4 - x 2 - 1 2 ∫ x 2 d x 1 4 - x 2 + 1 8 a r c sin (2 x) = = - 1 2 x 1 4 - x 2 - ∫ x 2 d x 1 - 4 x 2 + 1 8 a r c sin (2 x)

Сега нашето равенство изглежда така:

∫ x 2 d x 1 - 4 x 2 = - 1 2 x 1 4 - x 2 - ∫ x 2 d x 1 - 4 x 2 + 1 8 a r c sin (2 x)

Виждаме, че интегралът отдясно е подобен на този отляво. Преместваме го в друга част и получаваме:

2 ∫ x 2 d x 1 - 4 x 2 = - 1 2 x 1 4 - x 2 + 1 8 a r c sin (2 x) + C 1 ⇒ x 2 d x 1 - 4 x 2 = - 1 4 x 1 4 - x 2 + 1 16 a r c sin (2 x) + C 2 x 2 d x 1 - 4 x 2 = - 1 8 x 1 4 - x 2 + 1 16 a r c sin (2 x) + C 2

където C 2 = C 1 2

Да се върнем към оригиналните променливи:

∫ x · a r c sin (2 x) d x = x 2 2 a r c sin (2 x) - ∫ x 2 d x 1 - 4 x 2 = = x 2 2 a r c sin (2 x) - - 1 8 x 1 - 4 x 2 + 1 16 a r c sin (2 x) + C 2 = = 1 2 x 2 - 1 8 a r c sin (2 x) + 1 8 x 1 - 4 x 2 + C

където C = - C 2

Отговор:∫ x · a r c sin (2 x) d x = 1 2 x 2 - 1 8 a r c sin (2 x) + 1 8 x 1 - 4 x 2 + C .

Ако нашата задача съдържа интеграл от формата ∫ e a · x · sin (b x) d x или ∫ e a · x · cos (b x) d x , тогава всяка функция може да бъде избрана като u (x).

Пример 7

Изчислете неопределения интеграл ∫ e x · sin (2 x) d x .

Решение

∫ e x sin (2 x) d x = u (x) = sin (2 x) , d (v (x)) = e x d x d (u (x)) = 2 cos (2 x) d x , v (x) = ∫ e x d x = e x = = u (x) v (x) - ∫ v (x) d (u (x)) = sin (2 x) e x - ∫ e x 2 cos 2 x d x = = sin (2 x) e x - 2 ∫ e x cos (2 x) d x = u (x) = cos (2 x), d (v (x)) = e x d x d (u (x)) = - 2 sin (2 x) d x, v (x) = ∫ e x d x = e x = = sin (2 x) e x - 2 cos (2 x) e x - ∫ (e x (- 2 sin (2 x) d x)) = = sin (2 x) e x = 2 cos (2 x ) e x - 4 ∫ e x sin (2 x) d x

В резултат на това ще получим:

∫ e x sin (2 x) d x = sin (2 x) e x - 2 cos (2 x) e x - 4 ∫ e x sin (2 x) d x

Виждаме едни и същи интеграли отляво и отдясно, което означава, че можем да представим подобни термини:

5 ∫ e x sin (2 x) d x = sin (2 x) e x - 2 cos (2 x) e x ⇒ ∫ e x sin (2 x) d x = 1 5 sin (2 x) e x - 2 5 cos (2 x) e x + C

Отговор: ∫ e x sin (2 x) d x = 1 5 sin (2 x) e x - 2 5 cos (2 x) e x + C

Този метод на решение е стандартен, а отдясно често получавате интеграл, който е идентичен с оригиналния.

Разгледахме най-типичните задачи, в които можете точно да определите коя част от израза да приемете като d (v (x)) и коя част като u (x). В други случаи трябва да определите това сами.

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

Неопределен интеграл

1 Първопроизводен и неопределен интеграл 1

2 Най-простите свойства на неопределения интеграл. 3

Таблица на основните интеграли 3

2.1 Допълнителна таблица с интеграли 4

3 Замяна на променлива в неопределен интеграл 5

3.1 Метод за интегриране на функции от вида и (a≠ 0). 6

4 Интегриране по части в неопределен интеграл 7

4.1 Метод за интегриране на функции на формата. 7

4.2 Метод за интегриране на функции на формата: 8

5 Интегриране на рационални дроби 8

5.1 Метод за интегриране на прости дроби от тип 4. единадесет

6 Интегриране на ирационални изрази 12

6.1 Интегриране на тригонометрични изрази 14

Първопроизводен и неопределен интеграл

Решаване на диференциалното уравнение

на интервала, т.е. намираме функция, такава че . Тъй като , тогава уравнение (1) може да бъде пренаписано в диференциали:

Всяко решение на такова уравнение се нарича първоизводна на функция. Така функцията се извиква противопроизводна функцияна интервала, ако за всички. Не са изключени случаи и/или. Ясно е, че щом е антипроизводно, значи е и антипроизводно. Нашата задача е да намерим всички решения на уравнение (1). Функция на две променливи се нарича общо решение на уравнение (1) или, с други думи, неопределен интегралфункция, ако при заместване вместо което и да е число получим конкретно решение на уравнение (1) и всяко конкретно решение на уравнение (1) се получава по този начин.

Неопределеният интеграл се означава с . Функцията се нарича интегранд, диференциалът се нарича интегранд, а знакът на интеграла (разтегната латинска буква S, първата буква от думата Sum е sum). Възниква въпросът за съществуването на първоизводна и неопределен интеграл. В раздел „Определен интеграл“, § Формула на Нютон-Лайбниц, ще се докаже, че първопроизводната на непрекъсната функция винаги съществува.

Лема.Нека е еднакво за всички. Тогава е константа на този интервал.

Доказателство. Нека обозначим за всяка точка . Нека вземем произволна точка и приложим теоремата на Лагранж към разликата: за някаква точка . Това доказва лемата.□

Теорема за първоизводните. Две първоизводни на една и съща функция, дефинирани на интервал, се различават с константа.

Доказателство. Нека и са противопроизводни функции. Тогава откъде, според лемата -- постоянно. следователно . □

Последица. Ако е антипроизводна на функция, тогава .

Имайте предвид, че ако вземем не интервал като ODZ функция, а например такова несвързано множество като обединението на два интервала , Че всяка функция на формата

има нулева производна и по този начин лемата и теоремата за първоизводните престават да бъдат верни в този случай.

Най-простите свойства на неопределения интеграл.

1. Интегралът на сбора е равен на сбора на интегралите:

2. Константата може да бъде извадена от интегралния знак:

3. Производната на интеграла е равна на функцията интегранд.

4. Диференциалът на интеграла е равен на израза за интегранд.

5. (Линейна промяна на променливите) Ако , Че (Тук ).

Таблица на основните интеграли

В частност,

За изключителни случаи имаме:

Допълнителна таблица на интегралите

Промяна на променлива в неопределен интеграл

Нека разширим дефиницията на неопределения интеграл до по-общ случай: приемаме по дефиниция . Така напр

Теорема.Нека е диференцируема функция. Тогава

Доказателство. Позволявам . Тогава

което трябваше да се докаже.□

В специалния случай, когато получим линейна промяна на променливи (вижте свойство 5, §1). Прилагането на формула (1) „отляво надясно“ ще означава замяна на променлива. Прилагането на формула (1) в обратна посока, „отдясно наляво“, се нарича въвеждане под диференциалния знак.

Примери.А.

1. Изберете производната на квадратния трином в числителя:

3. За да изчислим първия интеграл в (2), използваме записа под диференциалния знак:

За да изчислим втория интеграл, ние избираме пълен квадрат в квадратния трином и го редуцираме до табличен, като използваме линейна промяна на променливи.

Същият метод се използва за изчисляване на интеграли на формата

Примери

Интегриране по части в неопределен интеграл

Теорема.За диференцируеми функции и връзката е валидна

Доказателство. Интегриране на лявата и дясната страна на формулата , получаваме:

Тъй като по дефиниция и , формула (1) следва.□

Пример.

За да интегрираме такива функции, въвеждаме полинома под диференциалния знак и прилагаме формулата за интегриране по части. Повтаряме процедурата k пъти.

Пример.

Интегриране на рационални дроби

Рационална дробсе нарича функция от формата , където са полиноми. Ако , тогава рационалната дроб се нарича правилно. Иначе се казва грешно.

Следните рационални дроби се наричат най-прости

(тип 2)

(тип 3)

(тип 4) ,

Теорема 1.Всяка дроб може да бъде разширена в сумата от полином и правилна рационална дроб.

Доказателство. Нека е неправилна рационална дроб. Нека разделим числителя на знаменателя с остатък: Тук има полиноми и тогава

Дробта е правилна поради неравенството. □

Теорема 2.Всяка правилна рационална дроб може да се разложи на проста сума.

Алгоритъм за разлагане.

а) Развиваме знаменателя на правилната дроб в произведението на нередуцируеми полиноми (линейни и квадратни с отрицателен дискриминант):

Тук и -- кратността на съответните корени.

б) Развиваме фракцията в сумата на най-простите с неопределени коефициенти съгласно следните принципи:

Правим това за всеки линеен фактор и за всеки квадратен фактор.

в) Умножаваме полученото разширение по общ знаменател и намираме неопределените коефициенти от условието, че лявата и дясната страна са идентични. Ние използваме комбинация от два метода

??? – обосновка на алгоритъма

Примери.А. Да разширим до сбора на най-простите

Следва, че . Замествайки в това съотношение веднага намираме . Така

Б. Нека разгънем рационалната дроб до сбора на най-простите. Развиването на тази дроб с неопределени коефициенти има формата

Умножавайки по общ знаменател, получаваме отношението

Замествайки тук, намираме откъде идва. Замествайки намираме . Приравнявайки коефициентите за получаваме системата

Следователно и. Събирайки равенствата на последната система, получаваме и . Тогава И

следователно

/**/ Задача.Обобщете резултата от пример А и докажете равенството

Метод за интегриране на прости дроби от тип 4.

а) Изолирайки производната на знаменателя в числителя, разширяваме интеграла в сумата от два интеграла.

б) Първият от получените интеграли, след като бъде въведен под знака на диференциала, ще стане табличен.

в) Във втория избираме пълен квадрат в знаменателя и редуцираме изчислението до интеграл от формата . Към този интеграл прилагаме следната рекурентна процедура

Към последния интеграл прилагаме формулата за интегриране по части:

Така че, ако дефинираме , Че

Това е рекурентна формула за изчисляване на интеграли, като се вземе предвид първоначалната стойност .

Пример

Интегриране на ирационални изрази

Интеграли на формата , където m/n,...,r/s са рационални числа с общ знаменател k, се редуцират до интеграла на рационална функция чрез заместване

Тогава те са рационални изрази, следователно след заместване се получава интегралът на рационалната дроб:

След като изчислим този интеграл (виж параграф 4) и направим обратното заместване, получаваме отговора.

По същия начин интегралите на формата

където ad-bc≠ 0 и k има същото значение като по-горе, се редуцират до интеграли на рационалната дроб чрез заместване

Примери. А. Нека изчислим интеграла

B. Изчислете интеграла

По-прост метод за интегриране (но изискващ догадки) на същата функция е:

Интегриране на тригонометрични изрази

Интеграли на формата се свеждат до интеграли на рационална функция чрез универсална замяна

следователно получаваме интеграла от рационалния израз

В специални случаи  R(sin x) cos x dx,  R(cos x) sin x dx и R(sin 2 x, cos 2 x, tan x, ctg x) dx е по-добре да се използват съответно замествания.

Този метод се основава на следната формула: (*)

Позволявам И - функции на x, имащи непрекъснати производни и .

Известно е, че или ; или .

Интеграли и , тъй като по условие функциите u и v са диференцируеми и следователно непрекъснати.

Формула (*) се нарича формула за интегриране по части.

Методът, основан на приложението му, се нарича метод на интегриране по части.

Той намалява изчислението до друг интеграл: .

Приложението на метода на интегриране по части е, че те се опитват да представят интегралния израз на даден интеграл под формата на продукт , където и са някои функции на x и тези функции са избрани така, че беше по-лесен за изчисляване от първоначалния интеграл. Кога за изчисление намери и .

(като „v“ вземаме една от оригиналните антипроизводни, открити от dv, така че в бъдеще, когато изчисляваме „v“, ще пропуснем константата C в нотацията).

Коментирайте.Когато разделяте интегрален израз на множители, трябва да разберете това и трябва да съдържате.

За съжаление е невъзможно да се дадат общи правила за разлагане на интегрален израз на фактори "u" и "dv". Много и обмислена практика може да научи това.

При всичко това трябва да се има предвид, че беше по-прост от оригиналния интеграл.

Пример 6.6.22.

Понякога, за да се получи крайният резултат, правилото за интегриране по части се прилага няколко пъти последователно.

Методът на интегриране по части, разбира се, не е удобен за използване всеки път и способността да се използва зависи от опита.

При изчисляване на интеграли е важно правилно да се установи кой метод на интегриране трябва да се използва (както в предишния пример, тригонометричното заместване води до целта по-бързо).

Нека разгледаме най-често срещаните интеграли, които се изчисляват чрез интегриране по части.

1.Интеграли на формата :

където е цяло число (спрямо x) полином; a е постоянно число.

Ако под интегралния знак има продукт на тригонометрична или експоненциална алгебрична функция, тогава алгебричната функция обикновено се приема като "u".

Пример 6.6.23.

Имайте предвид, че друга разбивка на фактори: не води до целта.

Доказано е
.

Нека получим по-сложен интеграл.

2.Интеграли на формата :

където е полином.

Ако под интегралния знак има произведение от логаритъм на функция или обратна тригонометрична функция и алгебрична, тогава функциите трябва да се приемат като "u".

Пример 6.6.23.

3.Интеграли от формата:

Тук можете да използвате всяка от 2 възможни разбивки на интегралния израз на фактори: за „u“ можете да вземете и двете, и .

Освен това изчисляването на такива интеграли, използвайки метода на интегриране по части, води до първоначалния интеграл, т.е. получава се уравнение по отношение на желания интеграл.

Пример 6.6.24. Пресметнете .

При интегриране често се налага последователно прилагане на метода на заместване и метода на интегриране по части.

Пример 6.6.25.

Интегриране на някои функции, съдържащи квадратен тричлен

и това са таблични интеграли.

2) коефициенти на реално число

в числителя избираме производната на знаменателя.

a,b,c – реални числа

А) ; тогава имаме:

б) . В този случай има смисъл да се разглежда само когато дискриминантът тричлен положителен:

Сега имаме:

Коментирайте. На практика те обикновено не използват готови резултати, а предпочитат да извършват подобни изчисления отново всеки път.

Пример.

Нека трансформираме числителя, така че да можем да извлечем производната на квадратния трином от него:

Поради факта, че на практика няма удобен общ метод за изчисляване на неопределени интеграли, е необходимо наред с частните методи за интегриране (виж предходната лекция) да се разгледат и методите за интегриране на някои отделни класове функции, интегралите на които често се срещат в практиката.

Най-важният клас сред тях е класът на рационалните функции.

"Интегриране на дробно-рационални функции"

Интегрирането на правилна рационална дроб се основава на разлагането на рационална дроб в сбор от елементарни дроби.

Елементарни (най-прости) дроби и тяхното интегриране.

Определение. Дроби от формата: ; (1)

(2), където

(т.е. корените на тричлена са сложни) се наричат елементарни.

Помислете за интегрирането на елементарни дроби

(където нека).

Нека изчислим интеграла

(*)

Последният интеграл се изчислява с помощта на рекурентна формула.

Понякога интегрирането по части ни позволява да получим връзка между неопределен интеграл, съдържащ степента на някаква функция и подобен интеграл, но с по-малка степен на същата функция. Такива отношения се наричат рекурентни формули.

Нека означим с .

Ние имаме:

В последния интеграл поставяме:

Ето защо

където

Така стигнахме до повтаряща се формула: многократното прилагане на която в крайна сметка води до „табуличен“ интеграл:

Тогава вместо “t” и “k” заместваме техните стойности.

Пример 6.6.26.

(по рекурентната формула).=

Рационалната дроб е функция, представима във формата ; където и са полиноми с реални коефициенти.

Рационалната дроб се нарича правилна, ако степента на числителя е по-малка от степента на знаменателя.

Всяка правилна рационална дроб може да бъде представена като сбор от краен брой елементарни дроби.

Разлагането на правилна дроб на елементарни се определя от следната теорема, която ще разгледаме без доказателство.

Теорема . Ако фракцията е правилно и , (където триномът няма реални корени), тогава идентичността е валидна:

(аз)

Обърнете внимание, че за всеки реален корен, например a, кратността " " на полинома в това разширение съответства на сбор от елементарни дроби от формата (1), а за всяка двойка комплексно спрегнати корени и (така че ) кратността " " - сбор от елементарни дроби от вида (2).

За да извършите разширение (I), трябва да се научите как да определяте коефициентите .

Има различни начини да ги намерите. Ще разгледаме метода на неопределените коефициенти и метода на частичните стойности.

Нека U(x) и V(x) са диференцируеми функции. Тогава d(U(x)V(x)) = U(x)dV(x) + V(x)dU(x) . Следователно U(x)dV(x) = d(U(x)V(x)) – V(x)dU(x) . Изчислявайки интеграла от двете страни на последното равенство, като вземем предвид факта, че ∫ d(U(x)V(x))=U(x)V(x)+C, получаваме отношението

Нарича се формула за интегриране по части. Разбира се в смисъл, че множеството от антипроизводни от лявата страна съвпада с множеството от антипроизводни, получени от дясната страна.

Приложение на метода на интегриране по части

Поради особеностите на намирането на определени количества, формулата за интегриране по части се използва много често в следните задачи:

Математическо очакване на непрекъсната случайна променлива. Формулата за намиране на математическото очакване и дисперсията на непрекъсната случайна променлива включва два фактора: полиномната функция на x и плътността на разпределението f(x).
Разширение в ред на Фурие. При разлагането е необходимо да се определят коефициентите, които се намират чрез интегриране на произведението на функцията f(x) и тригонометричната функция cos(x) или sin(x).

Типични разлагания по части

Когато използвате формулата за интегриране по части, трябва да изберете успешно U и dV, така че интегралът, получен от дясната страна на формулата, да бъде по-лесен за намиране. Нека поставим U=e x, dV=xdx в първия пример. Тогава dU=e x dx и Малко вероятно е интегралът ∫ x 2 e x dx да се счита за по-прост от оригиналния.
Понякога е необходимо да се приложи формулата за интегриране по части няколко пъти, например при изчисляване на интеграла ∫ x 2 sin(x)dx.