Лекция: Концепцията за производна функция, геометричен смисълпроизводна
Концепцията за производна функция
Нека разгледаме някаква функция f(x), която ще бъде непрекъсната през целия интервал на разглеждане. В разглеждания интервал избираме точката x 0, както и стойността на функцията в тази точка.

И така, нека да разгледаме графиката, на която отбелязваме нашата точка x 0, както и точката (x 0 + ∆x). Напомняме, че ∆х е разстоянието (разликата) между две избрани точки.
Също така си струва да се разбере, че всяко x съответства на собствената си стойност на функцията y.
Разликата между стойностите на функцията в точката x 0 и (x 0 + ∆x) се нарича нарастване на тази функция: ∆у = f(x 0 + ∆x) - f(x 0).
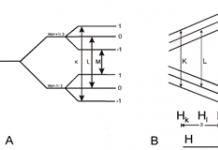
Нека обърнем внимание на допълнителната информация, която е налична на графиката - това е секансът, който се нарича KL, както и триъгълникът, който образува с интервали KN и LN.
Ъгълът, под който се намира секансът, се нарича неин ъгъл на наклон и се обозначава с α. Лесно може да се установи, че степенна мяркаъгъл LKN също е равен на α.
Сега нека си припомним връзките в правоъгълен триъгълник tgα = LN / KN = ∆у / ∆х.
Тоест тангенсът на секущия ъгъл е равен на отношението на нарастването на функцията към нарастването на аргумента.
В даден момент производната е границата на съотношението на нарастването на функция към нарастването на аргумента на безкрайно малки интервали.

Производната определя скоростта, с която функцията се променя в определена област.
Геометрично значение на производната
Ако намерите производната на която и да е функция в определена точка, можете да определите ъгъла, под който ще бъде разположена допирателната към графиката в даден ток спрямо оста OX. Обърнете внимание на графиката - тангенциалният ъгъл на наклона се обозначава с буквата φ и се определя от коефициента k в уравнението на правата линия: y = kx + b.
Тоест можем да заключим, че геометричното значение на производната е тангенсът на допирателния ъгъл в някаква точка на функцията.
Преди да прочетете информацията на текущата страница, препоръчваме да гледате видеоклип за производната и нейното геометрично значение
Вижте също пример за изчисляване на производната в точка
Допирателната към правата l в точка M0 е правата линия M0T - граничната позиция на секущата M0M, когато точката M клони към M0 по тази права (т.е. ъгълът клони към нула) по произволен начин.
Производна на функцията y = f(x)в точка х0 Нареченграницата на отношението на нарастването на тази функция към увеличението на аргумента, когато последният клони към нула. Производната на функцията y = f(x) в точката x0 и в учебниците се означава със символа f"(x0). Следователно по дефиниция
Терминът "дериват"(също "втора производна") въведен от Ж. Лагранж(1797), освен това той дава обозначенията y’, f’(x), f”(x) (1770,1779). Обозначението dy/dx се появява за първи път в Лайбниц (1675).
Производната на функцията y = f(x) при x = xо е равна на наклона на допирателната към графиката на тази функция в точката Mo(xo, f(xо)), т.е.
![]() къде - допирателен ъгъл
към оста Ox на правоъгълната декартова координатна система.
къде - допирателен ъгъл
към оста Ox на правоъгълната декартова координатна система.
 Уравнение на тангенс
към правата y = f(x) в точката Mo(xo, yo) приема формата
Уравнение на тангенс
към правата y = f(x) в точката Mo(xo, yo) приема формата
Нормалната към крива в дадена точка е перпендикулярът на допирателната в същата точка. Ако f(x0) не е равно на 0, тогава нормално уравнение на линията y = f(x) в точката Mo(ho, yo) ще бъде записано както следва:

Физическо значение на производната
Ако x = f(t) - закон праволинейно движениеточки, тогава x’ = f’(t) е скоростта на това движение в момент t. Дебитфизични, химични и други процесите се изразяват с помощта на производната.
Ако съотношението dy/dx за x->x0 има граница отдясно (или отляво), тогава то се нарича производна отдясно (съответно производна отляво). Такива граници се наричат едностранни производни.

 Очевидно функция f(x), дефинирана в определена околност на точката x0, има производна f’(x) тогава и само ако едностранните производни съществуват и са равни една на друга.
Очевидно функция f(x), дефинирана в определена околност на точката x0, има производна f’(x) тогава и само ако едностранните производни съществуват и са равни една на друга.
Геометрична интерпретация на производнататъй като наклонът на допирателната към графиката се отнася и за този случай: допирателната в в такъв случайуспоредна на оста Oy.
 За функция, която има производна в дадена точка, се казва, че е диференцируема в тази точка. Функция, която има производна във всяка точка от даден интервал, се нарича диференцируема в този интервал. Ако интервалът е затворен, то в краищата му има едностранни производни.
За функция, която има производна в дадена точка, се казва, че е диференцируема в тази точка. Функция, която има производна във всяка точка от даден интервал, се нарича диференцируема в този интервал. Ако интервалът е затворен, то в краищата му има едностранни производни.
Операцията за намиране на производната се нарича.
Нека започнем тази статия с общ преглед необходими определенияи концепции.
След това нека преминем към написването на уравнението на допирателната и даде подробни решениянай-типичните примери и задачи.
В заключение ще се съсредоточим върху намирането на уравнението на допирателната към криви от втори ред, тоест към окръжност, елипса, хипербола и парабола.
Навигация в страницата.
Дефиниции и понятия.
Определение.
Ъгъл на права линия y=kx+b е ъгълът, измерен от положителната посока на оста x до правата линия y=kx+b в положителната посока (т.е. обратно на часовниковата стрелка).

На фигурата положителната посока на оста x е показана с хоризонтална зелена стрелка, положителната посока на ъгъла е показана със зелена дъга, правата линия е показана със синя линия, а ъгълът на наклон на правата линията е показана с червена дъга.
Определение.
Наклон на права линия y=kx+b се нарича числов коефициент k.
Наклонът на права линия е равен на тангенса на ъгъла на наклона на правата линия, това е, .
Определение.
Директен AB, прекаран през две точки от графиката на функцията y=f(x), се нарича секуща. С други думи, секущае права линия, минаваща през две точки от графиката на функция.

На фигурата секущата AB е показана като синя линия, графиката на функцията y=f(x) е показана като черна крива, а ъгълът на наклона на секущата е показан като червена дъга.
Ако вземем предвид, че ъгловият коефициент на права линия е равен на тангенса на ъгъла на наклон (това беше обсъдено по-горе), а тангенсът на ъгъла в правоъгълен триъгълник ABC е съотношението на противоположния крак към съседен (това е дефиницията на тангенса на ъгъла), тогава поредица от равенства ще бъде вярна за нашия секанс ![]() , където са абсцисите на точки A и B,
, където са абсцисите на точки A и B, ![]() - съответните стойности на функцията.
- съответните стойности на функцията.
Това е, секущ ъгълсе определя от равенството  или
или  , А секущо уравнениенаписана във формуляра
, А секущо уравнениенаписана във формуляра  или
или  (ако е необходимо, вижте раздела).
(ако е необходимо, вижте раздела).
Секущата разделя графиката на функция на три части: вляво от точка A, от A до B и вдясно от точка B, въпреки че може да има повече от две общи точки с графиката на функцията.
Фигурата по-долу показва три действително различни секанса (точки A и B са различни), но те съвпадат и са дадени от едно уравнение.

Никога не сме срещали разговори за секуща за права линия. Но все пак, ако започнем от определението, тогава правата линия и нейната секуща съвпадат.
В някои случаи секансът може да има графика на функция безкраен бройпресечни точки. Например секансът, определен от уравнението y=0, има безкраен брой общи точки със синусоидата.
Определение.
Допирателна към графиката на функцията y=f(x) в точкатанаречена права линия, минаваща през точка, с сегмент от която графиката на функция практически се слива за стойности на x произволно близки до .
Нека обясним това определение с пример. Нека покажем, че правата y = x+1 е допирателна към графиката на функцията в точката (1; 2). За да направим това, ще покажем графики на тези функции, докато се приближаваме до точката на допиране (1; 2). Графиката на функцията е показана в черно, допирателната е показана като синя линия, а точката на допирателна е показана като червена точка.
Всеки следващ чертеж е уголемена област на предишния (тези области са подчертани с червени квадратчета).

Ясно се вижда, че близо до точката на допиране графиката на функцията практически се слива с допирателната y=x+1.
Сега нека преминем към по-смисленото определение на допирателната.
За да направим това, ще покажем какво ще се случи със секущата AB, ако точка B е безкрайно по-близо до точка A.
Фигурата по-долу илюстрира този процес.

Секансът AB (показан като синя пунктирана линия) ще се стреми да заеме позицията на допирателната към правата линия (показан като синя плътна линия), ъгълът на наклона на секанса (показан като червена пунктирана дъга) ще се стреми да ъгълът на наклона на тангентата (показан като плътна червена дъга).
Определение.
По този начин, допирателна към графиката на функцията y=f(x) в точка Aе граничната позиция на секанса AB при .
Сега можем да преминем към описание на геометричния смисъл на производната на функция в точка.
Геометричен смисъл на производната на функция в точка.
Нека разгледаме секанса AB на графиката на функцията y=f(x), така че точките A и B имат координати и съответно ![]() , където е нарастването на аргумента. Нека означим с нарастването на функцията. Нека маркираме всичко на чертежа:
, където е нарастването на аргумента. Нека означим с нарастването на функцията. Нека маркираме всичко на чертежа:

от правоъгълен триъгълникИмаме ABC. Тъй като по дефиниция допирателната е граничната позиция на секанса, тогава ![]() .
.
Нека си припомним дефиницията на производната на функция в точка: производната на функция y=f(x) в точка е границата на съотношението на нарастването на функцията към нарастването на аргумента в , означено ![]() .
.
следователно ![]() , където е наклонът на тангентата.
, където е наклонът на тангентата.
По този начин съществуването на производна на функцията y=f(x) в точка е еквивалентно на съществуването на допирателна към графиката на функцията y=f(x) в точката на допиране и наклонът на тангентата е равен на стойността на производната в точката, това е .
Заключаваме: геометричен смисъл на производната на функция в точкасе състои в съществуването на допирателна към графиката на функцията в тази точка.
Уравнение на допирателна.
За да напишете уравнението на която и да е права линия в равнина, е достатъчно да знаете нейния ъглов коефициент и точката, през която минава. Допирателната минава през точката на допиране и нейният ъглов коефициент за диференцируемата функция е равен на стойността на производната в точката. Тоест, от точката можем да вземем всички данни, за да напишем уравнението на допирателната.
Уравнение на допирателната към графиката на функцията y = f(x) в точкаизглежда като .
Предполагаме, че има крайна стойност на производната, в противен случай допирателната е права или вертикална (ако ![]() И
И ![]() ), или не съществува (ако
), или не съществува (ако ![]() ).
).
В зависимост от ъгловия коефициент, допирателната може да бъде успоредна на абсцисната ос (), успоредна на ординатната ос (в този случай уравнението на допирателната ще има формата), увеличаване () или намаляване ().
Време е да дадем няколко примера за пояснение.
Пример.
Напишете уравнение за допирателната към графиката на функцията  в точка (-1;-3) и определяне на ъгъла на наклон.
в точка (-1;-3) и определяне на ъгъла на наклон.
Решение.
Функцията е дефинирана за всички реални числа (вижте статията, ако е необходимо). Тъй като (-1;-3) е точка на допиране, тогава ![]() .
.
Намираме производната (за това материалът в статията, диференцираща функция, намирането на производната може да бъде полезен) и изчисляваме нейната стойност в точката: 
Тъй като стойността на производната в точката на допирателна е наклонът на допирателната и е равна на тангенса на ъгъла на наклон, тогава  .
.
Следователно ъгълът на наклона на допирателната е равен на  , а уравнението на допирателната има формата
, а уравнението на допирателната има формата 
Графична илюстрация.
Графиката на оригиналната функция е показана в черно, допирателната линия е показана като синя линия, а точката на допирателна е показана като червена точка. Картината вдясно е увеличен изглед на областта, обозначена с червения пунктиран квадрат на снимката вляво.

Пример.
Разберете дали има допирателна към графиката на функция ![]() в точка (1; 1), ако да, тогава съставете уравнението му и определете ъгъла му на наклон.
в точка (1; 1), ако да, тогава съставете уравнението му и определете ъгъла му на наклон.
Решение.
Домейнът на функция е цялото множество от реални числа.
Намиране на производната: 
Когато производната не е дефинирана, но  И
И  следователно в точка (1;1) има вертикална допирателна, нейното уравнение е x = 1, а ъгълът на наклон е равен на .
следователно в точка (1;1) има вертикална допирателна, нейното уравнение е x = 1, а ъгълът на наклон е равен на .
Графична илюстрация.

Пример.
Намерете всички точки на графиката на функцията, при които:
а) допирателната не съществува; б) допирателната е успоредна на оста х; в) допирателната е успоредна на правата.
Решение.
Както винаги, започваме с областта на дефиниране на функцията. В нашия пример функцията е дефинирана върху цялото множество от реални числа. Нека разширим знака за модул; за да направите това, разгледайте два интервала и: 
Нека разграничим функцията: 
При x=-2 производна не съществува, тъй като едностранните граници в тази точка не са равни: 
Така, след като сме изчислили стойността на функцията при x=-2, можем да дадем отговора на точка а): допирателната към графиката на функцията не съществува в точката (-2;-2).
б) Допирателната е успоредна на оста x, ако нейният наклон е нула (тангенсът на ъгъла на наклон е нула). защото ![]() , тогава трябва да намерим всички стойности на x, при които производната на функцията изчезва. Тези стойности ще бъдат абсцисата на допирателните точки, в които допирателната е успоредна на оста Ox.
, тогава трябва да намерим всички стойности на x, при които производната на функцията изчезва. Тези стойности ще бъдат абсцисата на допирателните точки, в които допирателната е успоредна на оста Ox.
Когато решим уравнението ![]() , и кога е уравнението
, и кога е уравнението ![]() :
:
Остава да се изчислят съответните стойности на функцията: 
Ето защо,  - необходимите точки от графиката на функцията.
- необходимите точки от графиката на функцията.
Графична илюстрация.
Графиката на оригиналната функция е изобразена с черна линия, с червени точки са отбелязани намерените точки, в които допирателните са успоредни на абсцисната ос.

в) Ако две прави в една равнина са успоредни, то ъгловите им коефициенти са равни (това е написано в статията). Въз основа на това твърдение трябва да намерим всички точки на графиката на функцията, при които наклонът на тангентата е равен на осем пети. Тоест трябва да решим уравнението. Така, когато решим уравнението ![]() , и кога е уравнението
, и кога е уравнението ![]() .
.
Дискриминантът на първото уравнение е отрицателен, следователно няма реални корени: 
Второто уравнение има две истински корени:
Намираме съответните стойности на функцията: 
По точки  допирателните към графиката на функция са успоредни на правата.
допирателните към графиката на функция са успоредни на правата.
Графична илюстрация.
Графиката на функцията е показана с черна линия, червената линия показва графиката на правата линия, сините линии показват допирателните към графиката на функцията в точки  .
.

За тригонометрични функциипоради тяхната периодичност може да има безкраен брой допирателни, които имат еднакъв наклон (еднакъв наклон).
Пример.
Напишете уравнения на всички допирателни към графиката на функцията  които са перпендикулярни на правата.
които са перпендикулярни на правата.
Решение.
За да създадем уравнение за допирателна към графиката на функция, трябва само да знаем нейния наклон и координатите на точката на допирателна.
Намираме ъгловия коефициент на допирателните от: произведението на ъгловите коефициенти на перпендикулярни прави линии е равно на минус едно, т.е. Тъй като по условие ъгловият коефициент на перпендикулярна права линия е равен на , тогава ![]() .
.
Нека започнем да намираме координатите на допирателните точки. Първо, нека намерим абсцисите, след което изчислим съответните стойности на функцията - това ще бъдат ординатите на допирателните точки.
Когато описваме геометричния смисъл на производната на функция в точка, отбелязахме това. От това равенство намираме абсцисата на допирателните точки. 
Стигнахме до тригонометрично уравнение. Моля, обърнете внимание на него, тъй като по-късно ще го използваме при изчисляване на ординатите на допирателните точки. Ние го решаваме (ако имате затруднения, моля, вижте раздела решение тригонометрични уравнения
):
Абсцисите на допирателните точки са намерени, нека изчислим съответните ординати (тук използваме равенството, на което ви помолихме да обърнете внимание точно по-горе): 
Така всички допирни точки. Следователно търсените допирателни уравнения имат формата: 
Графична илюстрация.
Фигурата на черната крива показва графиката на оригиналната функция върху сегмента [-10;10], сините линии изобразяват допирателните. Ясно се вижда, че са перпендикулярни на червената линия. Допирните точки са маркирани с червени точки.

Допирателна към окръжност, елипса, хипербола, парабола.
До този момент работихме върху намирането на уравнения за допирателни към графики на еднозначни функции от вида y = f(x) в различни точки. Каноничните уравнения на криви от втори ред не са еднозначни функции. Но ние можем да представим окръжност, елипса, хипербола и парабола чрез комбинация от две еднозначни функции и след това да съставим уравнения за допирателна според добре позната схема.
Допирателна към окръжност.
Окръжност с център в точка ![]() и радиус R е даден от .
и радиус R е даден от .
Нека запишем това равенство като обединение на две функции: 
Тук първата функция съответства на горния полукръг, втората - на долния.

Така, за да построим уравнението на допирателната към окръжността в точка, принадлежаща на горния (или долния) полукръг, намираме уравнението на допирателната към графиката на функцията (или) в посочената точка.
Лесно е да се покаже, че в точки от окръжност с координати ![]() И
И ![]() допирателните са успоредни на оста x и се дават от уравненията и съответно (на фигурата по-долу те са показани като сини точки и сини прави линии), а в точките
допирателните са успоредни на оста x и се дават от уравненията и съответно (на фигурата по-долу те са показани като сини точки и сини прави линии), а в точките ![]() И
И ![]() - са успоредни на ординатната ос и имат уравнения и съответно (на фигурата по-долу са отбелязани с червени точки и червени линии).
- са успоредни на ординатната ос и имат уравнения и съответно (на фигурата по-долу са отбелязани с червени точки и червени линии).

Допирателна към елипса.
Елипса с център в точка ![]() с полуоси a и b се дава от уравнението
с полуоси a и b се дава от уравнението  .
.
Елипса, също като кръг, може да се дефинира чрез комбиниране на две функции - горната и долната полуелипса: 

Допирателните при върховете на елипсата са успоредни или на абсцисната ос (показана като сини прави линии на фигурата по-долу), или на ординатната ос (показана като червени прави линии на фигурата по-долу).
Тоест горната полуелипса е дадена от функцията ![]() , а долната -
, а долната - ![]() .
.
Сега можем да използваме стандартния алгоритъм, за да съставим уравнение за допирателна към графиката на функция в точка.
Първа допирателна в точка: 
Втора допирателна в точка  :
:
Графична илюстрация.

Допирателна към хипербола.
Хипербола с център в точка ![]() и върхове
и върхове ![]() И
И ![]() се дава от равенството
се дава от равенството  (снимка долу вляво), и с върхове
(снимка долу вляво), и с върхове ![]() И
И ![]() - равенство
- равенство  (снимката долу вдясно).
(снимката долу вдясно).

Като комбинация от две функции хиперболата може да бъде представена като
 или
или  .
.

В върховете на хиперболата допирателните са успоредни на оста Oy за първия случай и успоредни на оста Ox за втория.
Така, за да намерим уравнението на допирателната към хиперболата, откриваме на коя функция принадлежи точката на допирателна и продължаваме по обичайния начин.
Възниква логичен въпрос: как да определим на коя функция принадлежи дадена точка. За да отговорим, заместваме координатите във всяко уравнение и виждаме кое от равенствата се превръща в идентичност. Нека да разгледаме това с пример.
Пример.
Напишете уравнение за допирателната към хиперболата ![]() в точка .
в точка .
Решение.
Нека напишем хиперболата под формата на две функции: 
Нека разберем на коя функция принадлежи точката на допир.
Следователно за първата функция точката не принадлежи на графиката на тази функция.
Следователно за втората функция точката принадлежи на графиката на тази функция.
Намерете ъгловия коефициент на тангентата: 
По този начин уравнението на допирателната има формата .
Графична илюстрация.

Тангента на парабола.
За да създадете уравнение за допирателна към парабола от формата ![]() в точка използваме стандартната схема и записваме уравнението на допирателната като . Допирателната към графиката на такава парабола при върха е успоредна на оста Ox.
в точка използваме стандартната схема и записваме уравнението на допирателната като . Допирателната към графиката на такава парабола при върха е успоредна на оста Ox.
Парабола ![]() Първо го дефинираме чрез комбиниране на две функции. За да направите това, нека решим това уравнение за y:
Първо го дефинираме чрез комбиниране на две функции. За да направите това, нека решим това уравнение за y: 

Сега откриваме на коя функция принадлежи допирателната точка и продължаваме по стандартната схема.
Допирателната към графиката на такава парабола във върха е успоредна на оста Oy.
За втората функция: 
Получаване на допирната точка  .
.
По този начин уравнението на желаната допирателна има формата  .
.
Цели на урока:
Студентите трябва да знаят:
- какво се нарича наклон на линия;
- ъгълът между правата и оста Ox;
- какъв е геометричният смисъл на производната;
- уравнение на допирателната към графиката на функция;
- метод за построяване на допирателна към парабола;
- да могат да прилагат теоретичните знания на практика.
Цели на урока:
Образователни: създаване на условия учениците да овладеят система от знания, умения и способности с понятията за механичен и геометричен смисъл на производната.
Образователни: формиране на научен мироглед у учениците.
Развитие: развиване на познавателния интерес, творчеството, волята, паметта, речта, вниманието, въображението, възприятието на учениците.
Методи за организиране на образователни и познавателни дейности:
- визуален;
- практичен;
- по умствена дейност: индуктивна;
- според усвояването на материала: частично търсене, репродуктивно;
- по степен на самостоятелност: лабораторни упражнения;
- стимулиращ: насърчаване;
- контрол: устно фронтално изследване.
План на урока
- Устни упражнения (намерете производната)
- Съобщение на ученик на тема „Причини за математически анализ”.
- Учене на нов материал
- Phys. Само минутка.
- Решаване на задачи.
- Лабораторна работа.
- Обобщаване на урока.
- Коментиране домашна работа.
Оборудване: мултимедиен проектор (презентация), карти ( лабораторна работа).
По време на часовете
„Човек постига нещо само там, където вярва в собствените си сили“
Л. Фойербах
I. Организационен момент.
Организация на класа през целия урок, готовност на учениците за урока, ред и дисциплина.
Поставяне на учебни цели на учениците, както за целия урок, така и за отделните му етапи.
Определете значението на изучавания материал както в тази тема, така и в целия курс.
Устно броене
1. Намерете производни:
", ()", (4sin x)", (cos2x)", (tg x)", "
2. Логически тест.
а) Въведете пропуснатия израз.
| 5x 3 -6x | 15x 2 -6 | 30x |
| 2sinx | 2cosx… | |
| cos2x | … … |
II. Съобщение на студента по темата „Причини за появата на математическия анализ“.
Общата посока на развитие на науката в крайна сметка се определя от изискванията на практиката на човешката дейност. Съществуването на древни държави със сложна йерархична система на управление би било невъзможно без достатъчното развитие на аритметиката и алгебрата, тъй като събирането на данъци, организирането на армейските доставки, изграждането на дворци и пирамиди и създаването на напоителни системи изискват сложни изчисления. През Ренесанса се разширяват връзките между различните части на средновековния свят, развиват се търговията и занаятите. Започва бързо нарастване на техническото ниво на производство и промишлено се използват нови източници на енергия, които не са свързани с мускулните усилия на хора или животни. През XI-XII век се появяват пълнежни и тъкачни машини, а в средата на XV - печатарска преса. Поради необходимостта от бързо развитиеобщественото производство през този период се променя същността на естествените науки, които от древността са имали описателен характер. Целта на естествознанието е задълбочено проучванеприродни процеси, а не предмети. Математиката, която оперира с постоянни величини, съответства на описателната естествена наука на древността. Беше необходимо да се създаде математически апарат, който да описва не резултата от процеса, а естеството на неговия поток и присъщите му модели. В резултат на това до края на 12 век Нютон в Англия и Лайбниц в Германия завършват първия етап от създаването на математическия анализ. Какво е "математически анализ"? Как могат да се характеризират и предвидят характеристиките на всеки процес? Използване на тези функции? За да проникнете по-дълбоко в същността на определено явление?
III. Учене на нов материал.
Нека да следваме пътя на Нютон и Лайбниц и да видим как можем да анализираме процеса, като го разглеждаме като функция на времето.
Нека представим няколко концепции, които ще ни помогнат допълнително.
Графиката на линейната функция y=kx+ b е права линия, числото k се нарича наклона на правата линия. k=tg, където е ъгълът на правата линия, тоест ъгълът между тази права линия и положителната посока на оста Ox.

Снимка 1

Разгледайте графиката на функцията y=f(x). Нека начертаем секанс през произволни две точки, например секанс AM. (фиг.2)
Ъглов коефициент на секущата k=tg. В правоъгълен триъгълник AMC<МАС = (объясните почему?). Тогда tg = = , что с точки зрения физики есть величина средней скорости протекания любого процесса на данном промежутке времени, например, скорости изменения расстояния в механике.

Фигура 2

Фигура 3
Самият термин "скорост" характеризира зависимостта на промяната на една величина от промяната на друга, като последната не е задължително да е време.
И така, тангенсът на ъгъла на наклона на секанса tg = .
Ние се интересуваме от зависимостта на промените в количествата за по-кратък период от време. Нека насочим нарастването на аргумента към нула. Тогава дясната страна на формулата е производната на функцията в точка А (обяснете защо). Ако x -> 0, тогава точка M се движи по графиката до точка A, което означава, че правата AM се доближава до някаква права линия AB, което е допирателна към графиката на функцията y = f(x) в точка A. (фиг.3)
Ъгълът на наклона на секанса клони към ъгъла на наклона на допирателната.
Геометричният смисъл на производната е, че стойността на производната в точка е равна на наклона на допирателната към графиката на функцията в точката.
Механично значение на производната.
Тангенсът на допирателния ъгъл е стойност, показваща моментната скорост на промяна на функцията в дадена точка, т.е. нова характеристика на процеса, който се изучава. Лайбниц нарече това количество производна, а Нютон каза, че самата производна се нарича моментна скорост.
IV. Физкултурна минута.
V. Решаване на проблеми.
№ 91 (1) страница 91 – покажете на дъската.
Ъгловият коефициент на допирателната към кривата f(x) = x 3 в точка x 0 – 1 е стойността на производната на тази функция при x = 1. f’(1) = 3x 2 ; f’(1) = 3.
No 91 (3.5) – диктовка.
No 92(1) – на дъската по желание.
№ 92 (3) – самостоятелно с устно изпитване.
№ 92 (5) – на дъската.
Отговори: 45 0, 135 0, 1,5 e 2.
VI. Лабораторна работа.
Цел: да се развие концепцията за „механично значение на производна“.
Приложения на производните в механиката.
Даден е законът за праволинейно движение на точката x = x(t), t.
- Средна скорост на движение за определен период от време;
- Скорост и ускорение в момент t 04
- Моменти на спиране; дали точката след момента на спиране продължава да се движи в същата посока или започва да се движи в обратна посока;
- Най-високата скорост на движение за определен период от време.
Работата се изпълнява по 12 варианта, като задачите са диференцирани по ниво на трудност (първият вариант е най-ниското ниво на трудност).
Преди започване на работа разговор по следните въпроси:
- Какъв е физическият смисъл на производната на изместването? (Скорост).
- Възможно ли е да се намери производната на скоростта? Тази величина използва ли се във физиката? Как се нарича? (Ускорение).
- Мигновена скоростравно на нула. Какво може да се каже за движението на тялото в този момент? (Това е моментът на спиране).
- Какъв е физическият смисъл на следните твърдения: производната на движението е равна на нула в точка t 0; променя ли производната знак при преминаване през точка t 0? (Тялото спира; посоката на движение се променя на противоположната).
Образец на студентска работа.
x(t)= t 3 -2 t 2 +1, t 0 = 2.

Фигура 4
В обратна посока.
Нека начертаем схематична диаграма на скоростта. В точката се постига най-висока скорост
t=10, v (10) =3· 10 2 -4· 10 =300-40=260

Фигура 5
VII. Обобщаване на урока
1) Какво е геометричното значение на производната?
2) Какво е механичното значение на производното?
3) Направете заключение за работата си.
VIII. Коментиране на домашни.
Страница 90. №91(2,4,6), №92(2,4,6,), стр.92 №112.
Използвани книги
- Учебник Алгебра и началото на анализа.
Автори: Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунина.
Под редакцията на А. Б. Жижченко. - Алгебра 11 клас. Урочни плановепо учебника на Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров. Част 1.
- Интернет ресурси: http://orags.narod.ru/manuals/html/gre/12.jpg
Резюме открит урокучител на GBPOU " Учителски колеж№ 4 Санкт Петербург"
Мартусевич Татяна Олеговна
Дата: 29.12.2014 г.
Тема: Геометричен смисъл на производните.
Тип урок: изучаване на нов материал.
Методи на обучение: визуално, частично търсене.
Целта на урока.
Въведете понятието допирателна към графиката на функция в точка, разберете какво е геометричното значение на производната, изведете уравнението на допирателната и научете как да го намерите.
Постигане на разбиране на геометричния смисъл на производната; извеждане на уравнението на допирателната; научете се да решавате основни проблеми;
осигурете повторение на материала по темата „Дефиниция на производна“;
създават условия за контрол (самоконтрол) на знанията и уменията.
Задачи за развитие:
насърчаване на формирането на умения за прилагане на техники за сравнение, обобщение и подчертаване на основното;
продължи развитието на математическите хоризонти, мисленето и речта, вниманието и паметта.
Образователни задачи:
насърчаване на интерес към математиката;
образование на активност, мобилност, комуникативни умения.
Тип урок – комбиниран урок с използване на ИКТ.
Оборудване – мултимедийна инсталация, презентацияMicrosoftМощностТочка.
Етап на урока
време
Дейности на учителя
Студентска дейност
1. Организационен момент.
Посочете темата и целта на урока.
Тема: Геометричен смисъл на производните.
Целта на урока.
Въведете понятието допирателна към графиката на функция в точка, разберете какво е геометричното значение на производната, изведете уравнението на допирателната и научете как да го намерите.
Подготовка на учениците за работа в клас.
Подготовка за работа в клас.
Разбиране на темата и целта на урока.
Водене на бележки.
2. Подготовка за усвояване на нов материал чрез повторение и актуализиране основни познания.
Организация на повторение и актуализиране на основни знания: дефиниране на производна и формулиране на нейния физически смисъл.
Формулиране на определението за производна и формулиране на физичния й смисъл. Повторение, актуализиране и затвърдяване на основни знания.

Организация на повторението и развитие на умението за намиране на производна степенна функцияи елементарни функции.
Намиране на производната на тези функции с помощта на формули.


Повторение на свойствата линейна функция.
Повторение, възприемане на рисунки и изявления на учителя
3. Работа с нов материал: обяснение.

Обяснение на значението на връзката между увеличението на функцията и увеличението на аргумента
Обяснение на геометричния смисъл на производната.
Въвеждане на нов материал чрез устни обяснения с помощта на изображения и визуални средства: мултимедийна презентация с анимация.
Възприемане на обяснение, разбиране, отговори на въпроси на учителя.
Формулиране на въпрос към учителя в случай на затруднение.

Възприемане на нова информация, нейното първично разбиране и разбиране.
Формулиране на въпроси към учителя в случай на затруднение.
Създаване на бележка.


Формулиране на геометричния смисъл на производната.
Разглеждане на три случая.
Водене на бележки, правене на чертежи.
4. Работа с нов материал.
Първично разбиране и прилагане на изучения материал, неговото затвърждаване.

В кои точки производната е положителна?
Отрицателна?
Равно на нула?
Обучение за намиране на алгоритъм за отговори на зададени въпроси по график.
Разбиране, осмисляне и прилагане на нова информация за решаване на проблем.
5. Първично разбиране и прилагане на изучения материал, неговото затвърдяване.

Съобщение на условията на задачата.
Записване на условията на задачата.
Формулиране на въпрос към учителя в случай на затруднение
6. Приложение на знанията: самостоятелна работа с учебен характер.
Решете проблема сами:

Приложение на придобитите знания.
Самостоятелна работавърху решаването на задачата за намиране на производната по чертеж. Обсъждане и проверка на отговорите по двойки, формулиране на въпрос към учителя при затруднение.
7. Работа с нов материал: обяснение.
Извеждане на уравнението на допирателна към графиката на функция в точка.


Подробно обяснение на извеждането на уравнението на допирателна към графиката на функция в точка, с помощта на мултимедийна презентация за нагледност и отговори на въпроси на учениците.
Извеждане на уравнението на допирателната съвместно с учителя. Отговори на въпросите на учителя.
Водене на бележки, създаване на рисунка.
8. Работа с нов материал: обяснение.

В диалог с учениците извеждане на алгоритъм за намиране на уравнението на допирателна към графиката на дадена функция в дадена точка.
В диалог с учителя изведете алгоритъм за намиране на уравнението на допирателната към графиката на дадена функция в дадена точка.
Водене на бележки.

Съобщение на условията на задачата.
Обучение в прилагане на придобитите знания.
Организиране на търсенето на начини за решаване на проблем и тяхното прилагане. подробен анализрешения с обяснение.
Записване на условията на задачата.
Правене на предположения за възможни начини за решаване на проблема при изпълнението на всеки елемент от плана за действие. Решаване на проблема заедно с учителя.
Записване на решението на задачата и отговора.
9. Приложение на знанията: самостоятелна работа с учебен характер.


Индивидуален контрол. Консултации и съдействие на учениците при необходимост.
Проверете и обяснете решението с помощта на презентация.
Приложение на придобитите знания.
Самостоятелна работа върху решаване на задача за намиране на производната по чертеж. Обсъждане и проверка на отговорите по двойки, формулиране на въпрос към учителя при затруднение
10. Домашна работа.
§48, задачи 1 и 3, разберете решението и го запишете в тетрадка, с рисунки.
№ 860 (2,4,6,8),
Съобщение за домашна работа с коментари.
Записване на домашни.
11. Обобщаване.
Повторихме дефиницията на производната; физическо значение на производната; свойства на линейна функция.
Научихме какво е геометричното значение на производната.
Научихме как да изведем уравнението на допирателна към графиката на дадена функция в дадена точка.
Корекция и изясняване на резултатите от урока.
Изброяване на резултатите от урока.
12. Рефлексия.
1. Намерихте урока: а) лесен; б) обикновено; в) трудно.
а) усвоил съм го напълно, мога да го прилагам;
б) научили са го, но трудно го прилагат;
в) не разбрах.
3. Мултимедийна презентация в клас:
а) помогна за овладяването на материала; б) не помогна за усвояването на материала;
в) пречи на усвояването на материала.
Провеждане на рефлексия.