Определение 13.1.Извиква се случайната променлива X отделен, ако приема краен или изброим брой стойности.
Определение 13.2. Закон за разпределение случайна величинахе колекция от двойки числа ( , ), където са възможните стойности на случайна променлива и са вероятностите, с които случайната променлива приема тези стойности, т.е. = P( х= ) и =1.
Най-простата формаДефиницията на дискретна случайна променлива е таблица, която изброява възможните стойности на случайната променлива и съответните вероятности. Тази таблица се нарича близко разпространениедискретна случайна променлива.
| х | … | … | |||
| Р | … | … |
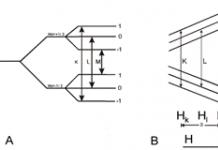
Разпределителните серии могат да бъдат изобразени графично. В този случай абсцисната ос е , а ординатната ос е вероятността . Точки с координати ( , ) се свързват с отсечки и се получава начупена линия, т.нар разпределителен полигон,което е една от формите за определяне на закона за разпределение на дискретна случайна променлива.
Пример 13.3.Конструирайте многоъгълник на разпределение на случайна променлива X със серия на разпределение
| х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
Определение 13.4.Те казват, че дискретна случайна променлива X има биномно разпределениес параметри ( n,p), ако може да приема неотрицателни цели числа к {1,2,…,н) с вероятности P( X=x)= .
Серията за разпространение изглежда така:
| х | … | к | … | н | ||
| Р | … | … |
Сума от вероятности = =1.
Определение 13.5.Дискретната форма на случайна променлива се нарича хТо има Поасоново разпределениес параметър (>0), ако приема цели числа к(0,1,2,...) с вероятности P( X=k)= .
Разпределителната серия има формата
| х | … | к | … | ||
| Р | … | … |
Тъй като разширението на серията Maclaurin има следващ изглед, тогава сумата от вероятностите = = =1.
Нека означим с хброй опити, които трябва да бъдат завършени преди събитието да се появи за първи път Ав независими опити, ако вероятността A да се появи във всеки от тях е еднаква стр (0<стр <1), а вероятность непоявления . Возможными значениями хса естествени числа.
Определение 13.6.Казват, че случайна променлива хТо има геометрично разпределениес параметър стр (0<стр <1), если она принимает натуральные значения к N с вероятности Р(Х=k)= , където . Диапазон на разпространение:
| х | … | н | … | |||
| Р | … | … |
Сума на вероятностите = = =1.
Пример 13.7.Монетата се хвърля 2 пъти. Съставете серия от разпределение на случайната променлива X брой срещания на „герба“.
P 2 (0)= = ; P 2 (1) = = =0,5; P 2 (2)= = .
| х | |||
| Р |
Серията на разпространение ще приеме формата:
Пример 13.8.Оръжието се стреля до първото попадение в целта. Вероятността за попадение с един изстрел е 0,6. Ще има попадение на 3-тия удар.
Тъй като стр=0,6, р=0,4, к=3, тогава P( А)= =0,4 2 *0,6=0,096.
14 Числени характеристики на дискретни случайни величини
Законът за разпределение напълно характеризира случайна променлива, но често е неизвестен, така че човек трябва да се ограничи до по-малко информация. Понякога дори е по-изгодно да се използват числа (параметри), които описват сумарно случайната променлива. Те се наричат числови характеристикислучайна величина. Те включват: математическо очакване, дисперсия и др.
Определение 14.1. Математическо очакванеДискретна случайна променлива е сумата от продуктите на всички възможни стойности и техните вероятности. Обозначава математическото очакване на случайна променлива хчрез М х=M( х)=E х.
Ако случайната променлива хприема краен брой стойности, тогава M х= .
Ако случайната променлива хприема изброим брой стойности, тогава M х= ,
Освен това математическото очакване съществува, ако редицата се сближава абсолютно.
Забележка 14.2.Математическото очакване е число, приблизително равно на определена стойност на случайна променлива.
Пример 14.3.Намерете математическото очакване на случайна променлива х, знаейки серията му за разпространение
| х | |||
| Р | 0,1 | 0,6 | 0,3 |
М х=3*0,1+5*0,6+2*0,3=3,9.
Пример 14.4.Намерете математическото очакване на броя на случванията на дадено събитие Ав един опит, ако вероятността от събитието Аравна на стр.
Случайна стойност х– номер на възникване на събитието Ав един тест. Може да приема стойности =1 ( Асе случи) с вероятност стри =0 с вероятност, т.е. серия за разпространение
Следователно MC=C*1=C.
Забележка 14.6.Произведение на постоянна променлива C и дискретна случайна променлива хДефинирана като дискретна случайна променлива C х, чиито възможни стойности са равни на произведенията на константата C и възможните стойности х, вероятностите на тези стойности C хравни на вероятностите на съответните възможни стойности х.
Имот 14.7.Постоянният фактор може да бъде изваден от знака за математическо очакване:
Г-ЦА х)=S∙M х.
Ако случайната променлива хима серия за разпространение
| х | … | … | |||
| Р | … | … |
Серия на разпределение на случайна променлива
| CX | … | … | |||
| Р | … | … |
Г-ЦА х)= = = С∙M( х).
Определение 14.8.Извикват се случайни променливи , ,… независима, ако за , аз=1,2,…,н
Р( , ,…, )= Р( ) Р( )… Р( ) (1)
Ако като =, аз=1,2,…,н, тогава получаваме от (1)
R(< , < ,…, < }= Р{ < }Р{ < }… Р{ < }, откуда получается другая формула:
( , ,…, ) = () ()... () (2)
за съвместната функция на разпределение на случайни променливи , ,…, , което може да се приеме и като дефиниция на независимостта на случайна променлива.
Имот 14.9.Математическо очакване на произведението от 2 независимаслучайни променливи е равно на произведението на техните математически очаквания:
М( XY)=М х∙М U.
Имот 14.10.Математическото очакване на сумата от 2 случайни променливи е равно на сумата от техните математически очаквания:
М( X+Y)=М х+М U.
Забележка 14.11.Свойства 14.9 и 14.10 могат да бъдат обобщени за случая на няколко случайни променливи.
Пример 14.12.Намерете математическото очакване на сумата от броя точки, които могат да се появят при хвърляне на 2 зара.
Позволявам хброя на точките, хвърлени на първия зар Uброя точки, хвърлени на втория зар. Те имат същата серия за разпространение:
| х | ||||||
| Р |
Тогава М х=М U= (1+2+3+4+5+6)= = . М( X+Y)=2* =7.
Теорема 14.13.Математическо очакване на броя на случванията на дадено събитие А V ннезависими опити е равно на произведението от броя опити и вероятността за възникване на събитие във всеки опит: M х=н.п..
Позволявам х– брой появявания на събитието А V ннезависими тестове. – брой повторения на събитието А V аз- този тест, аз=1,2,…,н.Тогава = + +…+ . Според свойствата на математическото очакване М х= . От пример 14.4 M X i=p,i=1,2,…,н,следователно М х= =н.п..
Определение 14.14.Дисперсияслучайна променлива се нарича числото D х=M( х-М х) 2 .
Определение 14.15.Стандартно отклонениеслучайна величина хизвикан номер =.
Забележка 14.16.Дисперсията е мярка за разпространението на стойностите на случайна променлива около нейното математическо очакване. Тя винаги е неотрицателна. За да изчислите дисперсията, е по-удобно да използвате друга формула:
д х= M( х-М х) 2 = M( х 2 - 2X∙М х+ (М х) 2) = M( х 2) - 2M( X∙М х) + M(M х) 2 = =M( х 2)-М X∙М X+(М х) 2 = М( х 2) - (М х) 2 .
Следователно Д х= M( х 2) - (М х) 2 .
Пример 14.17.Намерете дисперсията на случайна променлива х, дадени от серията за разпространение
| х | |||
| П | 0,1 | 0,6 | 0,3 |
М х=2*0,1+3*0,6+5*0,3=3,5; М( х 2)= 4*0,1+9*0,6+25*0,3=13,3;
д х=13.3-(3,5) 2 =1,05.
Дисперсионни свойства
Имот 14.18.Дисперсията на постоянна стойност е 0:
DC = M(C-MC) 2 = M(C-C) 2 =0.
Имот 14.19.Константният фактор може да бъде изваден от знака на дисперсията чрез повдигането му на квадрат
D(C х) =C 2 D х.
D(CX)=M(C-CM х) 2 =M(C(X- M х) 2) = C 2 M( х-М х) 2 = C 2 D х.
Имот 14.20.Дисперсия на сумата от 2 независимаслучайни променливи е равна на сбора от дисперсиите на тези променливи
Д( X+Y)=D х+D Y.
Д( X + Y)=M(( X+Y) 2) – (M( X+Y)) 2 = M( X2+ 2XY+Y2) - (М х+М Y) 2 = =M( х) 2 +2M хМ Y+M( Y 2)-(M( х) 2 +2M хМ Y+M( Y) 2)= M( х 2)-(М х) 2 +M( Y 2)-(М Y) 2 = = D х+D Y.
Следствие 14.21.Дисперсия на сумата от няколко независимаслучайни променливи е равна на сумата от техните дисперсии.
Теорема 14.22.Вариация на броя повторения на дадено събитие А V ннезависими тестове, във всеки от които вероятността p) 2 =). Следователно D +2,
СЛУЧАЙНИ ВЕЛИЧИНИ
Пример 2.1.Случайна стойност хдаден от функцията на разпределение
Намерете вероятността, че в резултат на теста хще приема стойности, съдържащи се в интервала (2.5; 3.6).
Решение: хв интервала (2.5; 3.6) може да се определи по два начина:
Пример 2.2.При какви стойности на параметрите АИ INфункция Е(х) = A + Be - xможе да бъде функция на разпределение за неотрицателни стойности на случайна променлива х.
Решение:Тъй като всички възможни стойности на случайната променлива хпринадлежат на интервала , тогава за да може функцията да бъде функция на разпределение за х, собствеността трябва да бъде удовлетворена:
![]() .
.
Отговор: ![]() .
.
Пример 2.3.Случайната променлива X се определя от функцията на разпределение

Намерете вероятността в резултат на четири независими теста стойността хточно 3 пъти ще приеме стойност, принадлежаща на интервала (0,25;0,75).
Решение:Вероятност за достигане на стойност хв интервала (0,25;0,75) намираме по формулата:
Пример 2.4.Вероятността топката да удари коша с един удар е 0,3. Съставете закон за разпределение на броя на попаденията с три хвърляния.
Решение:Случайна стойност х– броят на ударите в коша с три удара – може да приема следните стойности: 0, 1, 2, 3. Вероятностите, че х
х:
Пример 2.5.Двама стрелци стрелят по един изстрел в мишена. Вероятността първият стрелец да го уцели е 0,5, вторият - 0,4. Начертайте закон за разпределение на броя на попаденията в мишена.
Решение:Нека намерим закона за разпределение на дискретна случайна променлива х– брой попадения в целта. Нека събитието е първият стрелец, уцелил целта, и нека вторият стрелец уцели целта, и съответно техните пропуски.
Нека съставим закона за разпределение на вероятностите на SV х:
Пример 2.6.Тестват се три елемента, работещи независимо един от друг. Продължителността на времето (в часове) на безотказна работа на елементите има функция на плътност на разпределение: за първия: Е 1 (T) =1-д- 0,1 T, за второто: Е 2 (T) = 1-д- 0,2 T, за третото: Е 3 (T) =1-д- 0,3 T. Намерете вероятността, че в интервала от 0 до 5 часа: само един елемент ще се повреди; само два елемента ще се повредят; и трите елемента ще се провалят.
Решение:Нека използваме определението на функцията за генериране на вероятност:
Вероятността, че при независими опити, в първото от които вероятността за настъпване на събитие Аравно на , във второто и т.н. събитие Асе появява точно веднъж, равен на коефициента в разширението на генериращата функция по степени на . Нека намерим вероятностите за отказ и отказ съответно на първия, втория и третия елемент в интервала от 0 до 5 часа:
Нека създадем генерираща функция:
Коефициентът при е равен на вероятността събитието Аще се появи точно три пъти, тоест вероятността от повреда и на трите елемента; коефициентът при е равен на вероятността точно два елемента да се повредят; коефициентът при е равен на вероятността само един елемент да се повреди.
Пример 2.7.Като се има предвид плътността на вероятността f(х)случайна величина х:

Намерете функцията на разпределение F(x).
Решение:Използваме формулата:
![]() .
.
Така функцията на разпределение изглежда така:

Пример 2.8.Устройството се състои от три независимо работещи елемента. Вероятността за повреда на всеки елемент в един експеримент е 0,1. Начертайте закон за разпределение на броя на неуспешните елементи в един експеримент.
Решение:Случайна стойност х– броят на неуспешните елементи в един експеримент – може да приема следните стойности: 0, 1, 2, 3. Вероятности, че хприема тези стойности, намираме с помощта на формулата на Бернули:
Така получаваме следния закон за разпределение на вероятностите на случайна променлива х:
Пример 2.9.В партида от 6 части има 4 стандартни. 3 части бяха избрани на случаен принцип. Съставете закон за разпределение на броя на стандартните части между избраните.
Решение:Случайна стойност х– броя на стандартните части сред избраните – може да приема следните стойности: 1, 2, 3 и има хипергеометрично разпределение. Вероятности, че х

Където -- брой части в партидата;
-- брой стандартни части в партида;
– брой избрани части;
-- брой стандартни части сред избраните.
![]() .
.
![]() .
.
![]() .
.
Пример 2.10.Случайната променлива има плътност на разпределение

и не са известни, но , a и . Намерете и.
Решение:В този случай случайната променлива хима триъгълно разпределение (разпределение на Симпсън) на интервала [ а, б]. Числени характеристики х:
следователно ![]() . Решавайки тази система, получаваме две двойки стойности: . Тъй като според условията на проблема, накрая имаме:
. Решавайки тази система, получаваме две двойки стойности: . Тъй като според условията на проблема, накрая имаме: ![]() .
.
Отговор: ![]() .
.
Пример 2.11.Средно при 10% от договорите застрахователната компания изплаща застрахователни суми във връзка с настъпване на застрахователно събитие. Изчислете математическото очакване и дисперсията на броя на такива договори сред четири произволно избрани.
Решение:Математическото очакване и дисперсията могат да бъдат намерени с помощта на формулите:
![]() .
.
Възможни стойности на SV (брой договори (от четири) с настъпване на застрахователно събитие): 0, 1, 2, 3, 4.
Използваме формулата на Бернули, за да изчислим вероятностите за различен брой договори (от четири), за които са изплатени застрахователните суми:
![]() .
.
Серията за разпределение на IC (броят на договорите с настъпване на застрахователно събитие) има формата:
| 0,6561 | 0,2916 | 0,0486 | 0,0036 | 0,0001 |
Отговор: , .
Пример 2.12.От петте рози две са бели. Начертайте закон за разпределение на случайна променлива, изразяваща броя на белите рози между две едновременно взети.
Решение:В селекция от две рози може или да няма бяла роза, или да има една или две бели рози. Следователно, случайната променлива хможе да приема стойности: 0, 1, 2. Вероятности, че хприема тези стойности, намираме го по формулата:

Където -- брой рози;
-- брой бели рози;
– брой рози, взети по едно и също време;
-- броя на белите рози сред взетите.
![]() .
.
![]() .
.
![]() .
.
Тогава законът за разпределение на случайната променлива ще бъде както следва:
Пример 2.13.От 15-те сглобени единици 6 изискват допълнително смазване. Начертайте закон за разпределение на броя единици, които се нуждаят от допълнително смазване сред пет случайно избрани от общия брой.
Решение:Случайна стойност х– брой звена, които изискват допълнително смазване сред петте избрани – може да приема следните стойности: 0, 1, 2, 3, 4, 5 и има хипергеометрично разпределение. Вероятности, че хприема тези стойности, намираме го по формулата:

Където -- брой сглобени единици;
-- броя на единиците, които изискват допълнително смазване;
– брой избрани единици;
-- броя на единиците, които изискват допълнително смазване сред избраните.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Тогава законът за разпределение на случайната променлива ще бъде както следва:
Пример 2.14.От постъпилите за ремонт 10 часовника 7 изискват генерално почистване на механизма. Часовниците не са сортирани по вид ремонт. Майсторът, който иска да намери часовници, които се нуждаят от почистване, ги преглежда един по един и след като намери такива часовници, спира по-нататъшното гледане. Намерете математическото очакване и дисперсията на броя гледани часове.
Решение:Случайна стойност х– броя на единиците, които се нуждаят от допълнително смазване сред петте избрани – може да приеме следните стойности: 1, 2, 3, 4. Вероятности, че хприема тези стойности, намираме го по формулата:

![]() .
.
![]() .
.
![]() .
.
![]() .
.
Тогава законът за разпределение на случайната променлива ще бъде както следва:
Сега нека изчислим числените характеристики на количеството:
Отговор: , .
Пример 2.15.Абонатът е забравил последната цифра от телефонния номер, от който се нуждае, но помни, че е нечетен. Намерете математическото очакване и дисперсията на броя набирания на телефонен номер, преди да достигне до желания номер, ако набере последната цифра произволно и след това не набере набраната цифра.
Решение:Случайната променлива може да приема следните стойности: . Тъй като абонатът не набира набраната цифра в бъдеще, вероятностите за тези стойности са равни.
Нека съставим серия на разпределение на случайна променлива:
| 0,2 |
Нека изчислим математическото очакване и дисперсията на броя опити за набиране:
Отговор: , .
Пример 2.16.Вероятността от повреда по време на тестовете за надеждност за всяко устройство от серията е равна на стр. Определете математическото очакване на броя устройства, които са се провалили, ако са били тествани нустройства.
Решение:Дискретната случайна променлива X е броят на повредените устройства ннезависими тестове, при всеки от които вероятността за провал е еднаква п,разпределени по биномния закон. Математическото очакване на биномно разпределение е равно на броя опити, умножен по вероятността събитие да се случи в едно изпитване:
Пример 2.17.Дискретна случайна променлива хприема 3 възможни стойности: с вероятност ; с вероятност и с вероятност. Намерете и , знаейки, че M( х) = 8.
Решение:Ние използваме дефинициите на математическото очакване и закона за разпределение на дискретна случайна променлива:

Намираме: .
Пример 2.18.Отделът за технически контрол проверява продуктите за стандартност. Вероятността продуктът да е стандартен е 0,9. Всяка партида съдържа 5 продукта. Намерете математическото очакване на случайна променлива х– броя на партидите, всяка от които съдържа точно 4 стандартни продукта, ако на проверка подлежат 50 партиди.
Решение:В този случай всички проведени експерименти са независими и вероятностите всяка партида да съдържа точно 4 стандартни продукта са еднакви, следователно математическото очакване може да се определи по формулата:
![]() ,
,
къде е броят на партиите;
Вероятността една партида да съдържа точно 4 стандартни продукта.
Намираме вероятността с помощта на формулата на Бернули:
Отговор: ![]() .
.
Пример 2.19.Намерете дисперсията на случайна променлива х– брой появявания на събитието Ав две независими изпитвания, ако вероятностите за настъпване на събитие в тези изпитвания са еднакви и е известно, че М(х) = 0,9.
Решение:Проблемът може да се реши по два начина.
1) Възможни стойности на SV х: 0, 1, 2. Използвайки формулата на Бернули, ние определяме вероятностите за тези събития:
,
![]() ,
.
,
.
След това законът за разпределение хима формата:
От дефиницията на математическото очакване определяме вероятността:
Нека намерим дисперсията на SV х:
![]() .
.
2) Можете да използвате формулата:
![]() .
.
Отговор: ![]() .
.
Пример 2.20.Очакване и стандартно отклонение на нормално разпределена случайна променлива хсъответно равни на 20 и 5. Намерете вероятността в резултат на теста хще приеме стойността, съдържаща се в интервала (15; 25).
Решение:Вероятност за попадение на нормална случайна променлива хна участъка от до се изразява чрез функцията на Лаплас:
Пример 2.21.Дадена функция: 
При каква стойност на параметъра ° Стази функция е плътността на разпределение на някаква непрекъсната случайна променлива х? Намерете математическото очакване и дисперсията на случайна променлива х.
Решение:За да бъде функцията плътност на разпределение на някаква случайна променлива, тя трябва да е неотрицателна и трябва да отговаря на свойството:
![]() .
.
Следователно:
Нека изчислим математическото очакване по формулата:
![]() .
.
Нека изчислим дисперсията по формулата:
Т е равно стр. Необходимо е да се намери математическото очакване и дисперсията на тази случайна променлива.
Решение:Законът за разпределение на дискретна случайна променлива X - броят на случванията на събитие в независими опити, при всяко от които вероятността събитието да се случи е равна на , се нарича бином. Математическото очакване на биномното разпределение е равно на произведението от броя опити и вероятността за възникване на събитие А в едно изпитване:
![]() .
.
![]()
Пример 2.25.Произвеждат се три независими изстрела по целта. Вероятността за уцелване на всеки удар е 0,25. Определете стандартното отклонение на броя на попаденията с три изстрела.
Решение:Тъй като се извършват три независими опита и вероятността за възникване на събитие А (попадение) във всяко изпитание е една и съща, ще приемем, че дискретната случайна променлива X - броят на попаденията в целта - е разпределена според биномен закон.
Дисперсията на биномното разпределение е равна на произведението от броя на опитите и вероятността за настъпване и ненастъпване на събитие в един опит:
![]()
Пример 2.26.Средният брой клиенти, посещаващи застрахователна компания за 10 минути, е трима. Намерете вероятността поне един клиент да пристигне през следващите 5 минути.
Среден брой клиенти, пристигащи за 5 минути: ![]() . .
. .
Пример 2.29.Времето за изчакване на приложение в опашката на процесора се подчинява на експоненциален закон на разпределение със средна стойност 20 секунди. Намерете вероятността следващата (произволна) заявка да изчака на процесора повече от 35 секунди.
Решение:В този пример, математическото очакване ![]() , а степента на отказ е равна на .
, а степента на отказ е равна на .
Тогава желаната вероятност:
Пример 2.30.Група от 15 студенти провежда среща в зала с 20 реда по 10 места. Всеки ученик заема място в залата на случаен принцип. Каква е вероятността не повече от трима души да са на седмо място в редицата?
Решение:
Пример 2.31.
Тогава, според класическата дефиниция на вероятността:

Където -- брой части в партидата;
-- брой нестандартни части в партидата;
– брой избрани части;
-- брой нестандартни части сред избраните.
Тогава законът за разпределение на случайната променлива ще бъде както следва.
Нека проверим дали е изпълнено изискването за равномерна ограниченост на дисперсията. Нека напишем закона за разпределение  :
:
|
|
|
|
|
|
|
Нека намерим математическото очакване  :
:
Нека намерим дисперсията  :
:
Тази функция се увеличава, така че за да изчислите константата, която ограничава дисперсията, можете да изчислите границата:

По този начин вариациите на дадените случайни променливи са неограничени, което трябваше да се докаже.
Б) От формулировката на теоремата на Чебишев следва, че изискването за равномерна ограниченост на дисперсиите е достатъчно, но не е необходимо условие, следователно не може да се твърди, че тази теорема не може да се приложи към дадена последователност.
Последователността от независими случайни променливи X 1, X 2, ..., X n, ... е дадена от закона за разпределение
![]()
D(X n)=M(X n 2)- 2,
имайте предвид, че M(X n) = 0, ще намерим (изчисленията са оставени на читателя)
![]()
Нека временно приемем, че n се променя непрекъснато (за да подчертаем това предположение, обозначаваме n с x) и изследваме функцията φ(x) = x 2 /2 x-1 за екстремум.
Приравнявайки първата производна на тази функция на нула, намираме критичните точки x 1 = 0 и x 2 = ln 2.
Нека отхвърлим първата точка, тъй като не представлява интерес (n не приема стойност, равна на нула); лесно се вижда, че в точки x 2 =2/ln 2 функцията φ(x) има максимум. Като се има предвид, че 2/ln 2 ≈ 2,9 и че N е положително цяло число, ние изчисляваме дисперсията D(X n)= (n 2 /2 n -1)α 2 за целите числа, най-близки до числото 2,9 (отляво и дясно), т.е. за n=2 и n=3.
За n=2, дисперсия D(X 2)=2α 2, за n=3 дисперсия D(X 3)=9/4α 2. очевидно,
(9/4)α 2 > 2α 2 .
Така най-голямата възможна дисперсия е (9/4)α 2, т.е. дисперсиите на случайните променливи Xn са равномерно ограничени от числото (9/4)α 2 .
Последователността от независими случайни променливи X 1 , X 2 , …, X n , … е дадена от закона за разпределение
![]()
Приложима ли е теоремата на Чебишев за дадена последователност?
Коментирайте. Тъй като случайните променливи X са еднакво разпределени и независими, читателят, запознат с теоремата на Хинчин, може да се ограничи до изчисляване само на математическото очакване и да се увери, че то е пълно.
Тъй като случайните променливи X n са независими, те са дори по двойки независими, т.е. първото изискване на теоремата на Чебишев е изпълнено.
Лесно се установява, че M(X n)=0, т.е. първото изискване за крайност на математическите очаквания е изпълнено.
Остава да проверим дали е изпълнено изискването за равномерна ограниченост на дисперсиите. Според формулата
D(X n)=M(X n 2)- 2,
вземем предвид, че M(X n)=0, намираме
Така най-голямата възможна дисперсия е 2, т.е. дисперсиите на случайните променливи X n са равномерно ограничени от числото 2.
Така че всички изисквания на теоремата на Чебишев са изпълнени, следователно тази теорема е приложима към разглежданата последователност.

Намерете вероятността в резултат на теста стойността на X да приеме стойност, съдържаща се в интервала (0, 1/3).
Случайната променлива X е определена върху цялата ос Ox чрез функция, разпределена F(x)=1/2+(arctg x)/π. Намерете вероятността в резултат на теста стойността на X да приеме стойност, съдържаща се в интервала (0, 1). Вероятността X да приеме стойност, съдържаща се в интервала (a, b), е равна на нарастването на функцията на разпределение на този интервал: P(a P(0<
Х <1) = F(1)-F(0)
= x =1 -
x =0
= 1/4 Функция на разпределение X на случайна променлива Намерете вероятността в резултат на теста стойността на X да приеме стойност, съдържаща се в интервала (-1, 1). Вероятността X да приеме стойност, съдържаща се в интервала (a, b), е равна на нарастването на функцията на разпределение на този интервал: P(a P(-1<
Х <1) = F(1)-F(-1)
= x =-1
– x =1
= 1/3. Функцията на разпределение на непрекъсната случайна променлива X (време за безотказна работа на някое устройство) е равна на F(x)=1st -x/ T (x≥0). Намерете вероятността за безотказна работа на устройството за време x≥T. Вероятността X да приеме стойност, съдържаща се в интервала x≥T, е равна на нарастването на функцията на разпределение на този интервал: P(0 P(x≥T) = 1 - P(T Случайната променлива X се определя от функцията на разпределение Намерете вероятността в резултат на теста X да приеме стойност: а) по-малка от 0,2; б) по-малко от три; в) най-малко три; г) най-малко пет. а) Тъй като за x≤2 функцията F(x)=0, то F(0, 2)=0, т.е. P(x< 0, 2)=0; б) P(X< 3) = F(3) = x =3
= 1.5-1 = 0.5; в) събития X≥3 и X<3 противоположны,
поэтому Р(Х≥3)+Р(Х<3)=1. Отсюда, учитывая,
что Р(Х<3)=0.5 [см. п. б.], получим Р(Х≥3) =
1-0.5 = 0.5; г) сумата от вероятностите за противоположни събития е равна на единица, следователно P(X≥5)+P(X<5)=1. Отсюда, используя условие,
в силу которого при х>4 функция F(x)=1, получаваме P(X≥5) = 1-P(X<5) = 1-F(5)
= 1-1 = 0. Случайната променлива X се определя от функцията на разпределение Намерете вероятността в резултат на четири независими опита стойността на X да приеме стойност, принадлежаща на интервала (0,25, 0,75) точно три пъти. Вероятността X да приеме стойност, съдържаща се в интервала (a, b), е равна на нарастването на функцията на разпределение на този интервал: P(a P(0,25< X <0.75) =
F(0.75)-F(0.25) =
0.5 Следователно, , или Случайната променлива X е определена по цялата ос Ox чрез функцията на разпределение. Намерете възможна стойност, която удовлетворява условието: с вероятност случайният X в резултат на теста ще приеме по-голяма стойност Решение. Събитията и са противоположни, следователно . Следователно, . От тогава. По дефиниция на функцията на разпределение, . Следователно, , или Дискретната случайна променлива X е дадена от закона за разпределение И така, търсената функция на разпределение има формата Дискретната случайна променлива X е дадена от закона за разпределение Намерете функцията на разпределение и начертайте нейната графика. Дадена е функцията на разпределение на непрекъсната случайна променлива X Намерете плътността на разпределение f(x). Плътността на разпределение е равна на първата производна на функцията на разпределение: Непрекъсната случайна променлива X се определя от плътността на разпределение в интервала; извън този интервал. Намерете вероятността X да приеме стойност, принадлежаща на интервала. Нека използваме формулата. По условие и. Следователно, необходимата вероятност Непрекъсната случайна променлива X се дава от плътността на разпределението Нека използваме формулата. По условие и Плътността на разпределение на непрекъсната случайна променлива X в интервала (-π/2, π/2) е равна на f(x)=(2/π)*cos2x ; извън този интервал f(x)=0. Намерете вероятността в три независими опита X да приеме точно два пъти стойността, съдържаща се в интервала (0, π/4). Нека използваме формулата P(a P(0 Отговор: π+24π. fx=0, при x≤0cosx, при 0 Използваме формулата Ако x ≤0, тогава f(x)=0, следователно, F(x)=-∞00dx=0. Ако 0 F(x)=-∞00dx+0xcosxdx=sinx. Ако x≥ π2, тогава F(x)=-∞00dx+0π2cosxdx+π2x0dx=sinx|0π2=1. И така, необходимата функция на разпределение Fx=0, при x≤0sinx, при 0 Плътността на разпределение на непрекъсната случайна променлива X е дадена: Fx=0, при x≤0sinx, при 0 Намерете функцията на разпределение F(x). Използваме формулата Плътността на разпределение на непрекъсната случайна променлива X се определя по цялата ос Ox от равенството . Намерете постоянния параметър C. По този начин, Плътността на разпределение на непрекъсната случайна променлива се определя по цялата ос чрез равенството Намерете постоянния параметър C. Решение. Плътността на разпределение трябва да отговаря на условието. Изискваме това условие да бъде изпълнено за дадената функция: Нека първо намерим неопределения интеграл: След това изчисляваме неправилния интеграл: По този начин, Замествайки (**) в (*), накрая получаваме . Плътността на разпределение на непрекъсната случайна величина X в интервала е равна на ; извън този интервал f(x) = 0. Намерете постоянния параметър C. Нека първо намерим неопределения интеграл: След това изчисляваме неправилния интеграл: Замествайки (**) в (*), накрая получаваме . Плътността на разпределение на непрекъсната случайна величина X се задава в интервала с равенството ; извън този интервал f(x) = 0. Намерете постоянния параметър C. Решение. Плътността на разпределение трябва да отговаря на условието, но тъй като f(x) извън интервала е равно на 0, достатъчно е тя да удовлетворява: Нека първо намерим неопределения интеграл: След това изчисляваме неправилния интеграл: Замествайки (**) в (*), накрая получаваме . Случайната променлива X се определя от плътността на разпределение ƒ(x) = 2x в интервала (0,1); извън този интервал ƒ(x) = 0. Намерете математическото очакване на стойността X. Р Като заместим a = 0, b = 1, ƒ(x) = 2x, получаваме Отговор: 2/3. Случайната променлива X се определя от плътността на разпределение ƒ(x) = (1/2)x в интервала (0;2); извън този интервал ƒ(x) = 0. Намерете математическото очакване на стойността X. Р Замествайки a = 0, b = 2, ƒ(x) = (1/2)x, получаваме M(X) = Отговор: 4/3. Случайната променлива X в интервала (–s, s) се определя от плътността на разпределение ƒ Р Замествайки a = –с, b = c, ƒ(x) = , получаваме Като се има предвид, че интегралната функция е нечетна и границите на интеграцията са симетрични спрямо началото, ние заключаваме, че интегралът е равен на нула. Следователно, M(X) = 0. Този резултат може да се получи незабавно, ако вземем предвид, че кривата на разпределение е симетрична по отношение на правата линия x = 0. Случайната променлива X в интервала (2, 4) се определя от плътността на разпределение f(x)= Случайната променлива X в интервала (3, 5) се определя от плътността на разпределение f(x)= Решение. Нека представим плътността на разпределение във формата Случайната променлива X в интервала (-1, 1) се определя от плътността на разпределение 2. ОПИСАНИЕ НА НЕСИГУРНОСТИТЕ В ТЕОРИЯТА ЗА ВЗЕМАНЕ НА РЕШЕНИЯ 2.2.4. Случайни величини и техните разпределения Разпределения на случайни величини и функции на разпределение. Разпределението на числова случайна променлива е функция, която еднозначно определя вероятността случайната променлива да приеме дадена стойност или да принадлежи към даден интервал. Първият е, ако случайната променлива приема краен брой стойности. Тогава разпределението е дадено от функцията P(X = x),присвояване на всяка възможна стойност хслучайна величина хвероятността, че X = x. Второто е, ако случайната променлива приема безкрайно много стойности. Това е възможно само когато вероятностното пространство, върху което е дефинирана случайната променлива, се състои от безкраен брой елементарни събития. Тогава разпределението се дава от набор от вероятности P(a <
х P(a <
х Тази връзка показва, че както разпределението може да се изчисли от функцията на разпределението, така и, обратно, функцията на разпределението може да се изчисли от разпределението. Функциите на разпределение, използвани във вероятностно-статистическите методи за вземане на решения и други приложни изследвания, са дискретни, непрекъснати или комбинации от тях. Дискретните функции на разпределение съответстват на дискретни случайни променливи, които приемат краен брой стойности или стойности от набор, чиито елементи могат да бъдат номерирани с естествени числа (такива набори се наричат изброими в математиката). Тяхната графика изглежда като стъпаловидна стълба (фиг. 1). Пример 1.Номер хдефектните елементи в партида приемат стойност 0 с вероятност 0,3, стойност 1 с вероятност 0,4, стойност 2 с вероятност 0,2 и стойност 3 с вероятност 0,1. Графика на функцията на разпределение на случайна променлива хпоказано на фиг. 1. Фиг. 1. Графика на функцията на разпределение на броя на дефектните продукти. Непрекъснатите функции на разпределение нямат скокове. Те нарастват монотонно с увеличаване на аргумента - от 0 при до 1 при . Случайни променливи, които имат непрекъснати функции на разпределение, се наричат непрекъснати. Непрекъснатите функции на разпределение, използвани във вероятностно-статистическите методи за вземане на решения, имат производни. Първа производна f(x)разпределителни функции F(x)се нарича плътност на вероятността, Използвайки плътността на вероятността, можете да определите функцията на разпределение: За всяка функция на разпределение и следователно Изброените свойства на функциите на разпределение се използват постоянно във вероятностните и статистическите методи за вземане на решения. По-специално, последното равенство предполага специфична форма на константи във формулите за вероятностни плътности, разгледани по-долу. Пример 2.Често се използва следната функция на разпределение: Където аИ b– някои числа, а . Нека намерим плътността на вероятността на тази функция на разпределение: (в точки х = аИ x = bпроизводна на функция F(x)не съществува). Случайна променлива с функция на разпределение (1) се нарича „равномерно разпределена на интервала [ а; b]». Смесени функции на разпределение възникват, по-специално, когато наблюденията спрат в някакъв момент. Например, когато се анализират статистически данни, получени от използването на планове за тестове за надеждност, които предвиждат прекратяване на тестването след определен период. Или при анализиране на данни за технически продукти, изискващи гаранционен ремонт. Пример 3.Нека например експлоатационният живот на електрическа крушка е случайна величина с функция на разпределение F(t),и тестът се провежда, докато електрическата крушка се повреди, ако това се случи след по-малко от 100 часа от началото на теста, или докато t 0= 100 часа. Позволявам G(t)– функция на разпределение на времето на работа на електрическата крушка в добро състояние по време на това изпитване. Тогава функция G(t)има скок в точка t 0, тъй като съответната случайна променлива приема стойността t 0с вероятност 1- F(t 0)> 0.
Характеристики на случайните величини.При вероятностно-статистическите методи за вземане на решения се използват редица характеристики на случайни величини, изразени чрез функции на разпределение и плътности на вероятности. При описване на диференциацията на доходите, при намиране на доверителни граници за параметрите на разпределението на случайни променливи и в много други случаи се използва понятието като „квантил на реда“. Р“, където 0< стр < 1 (обозначается x p). Квантил на поръчката Р– стойността на случайна променлива, за която функцията на разпределение приема стойност Рили има „скок“ от по-малка стойност Рна по-голяма стойност Р(фиг. 2). Може да се случи това условие да е изпълнено за всички стойности на x, принадлежащи на този интервал (т.е. функцията на разпределение е постоянна на този интервал и е равна на Р). Тогава всяка такава стойност се нарича „квантил от ред“ Р». Фиг.2. Дефиниция на квантил x pпоръчка Р. За функциите на непрекъснато разпределение по правило има един квантил x pпоръчка Р(фиг. 2) и F(x p) = p. (2) Пример 4.Нека намерим квантила x pпоръчка Рза разпределителната функция F(x)от (1). На 0< стр <
1 квантиль x pсе намира от уравнението тези. x p
= a + p(b – a) = a( 1-
p) +bp. При стр= 0 всякакви х <
ае квантил от ред стр= 0. Квантил на поръчката стр= 1 е всяко число х >
b. За дискретни разпределения, като правило, няма x p, удовлетворяващ уравнение (2). По-точно, ако разпределението на случайна променлива е дадено в таблица 1, където х 1< x 2 < … < x k
, тогава равенство (2), разглеждано като уравнение по отношение на x p, има решения само за кстойности стр, а именно p = p 1, p = p 1 + p 2, p = p 1 + p 2 + p 3, p = p 1 + p 2 + … + p m , 3< m < k,
p = p 1 + p 2 + … + p k . Маса 1. Разпределение на дискретна случайна величина Стойности хслучайна величина х Вероятности P(X =x) За изброените квероятностни стойности стррешение x pуравнение (2) не е уникално, а именно, F(x) = p 1 + p 2 + … + p m за всички хтакова, че x m< x <
x m+1.Тези. x p –всяко число от интервала (x m; x m+1].За всички останали Рот интервала (0;1), невключен в списъка (3), има „скок“ от стойност по-малка Рна по-голяма стойност Р. А именно, ако p 1 + p 2 + … + p m Че x p = x m+1. Разглежданото свойство на дискретни разпределения създава значителни трудности при таблично изготвяне и използване на такива разпределения, тъй като е невъзможно да се поддържат точно типичните числени стойности на характеристиките на разпределението. По-специално, това е вярно за критичните стойности и нивата на значимост на непараметричните статистически тестове (вижте по-долу), тъй като разпределенията на статистиките на тези тестове са дискретни. Квантилният ред е от голямо значение в статистиката Р= S. Нарича се медиана (случайна променлива хили неговите разпределителни функции F(x))и е обозначен Аз (X).В геометрията има понятието "медиана" - права линия, минаваща през върха на триъгълник и разделяща противоположната му страна наполовина. В математическата статистика медианата дели наполовина не страната на триъгълника, а разпределението на случайна променлива: равенство F(x 0,5)= 0,5 означава, че вероятността да стигнете наляво х 0,5и вероятността да стигнете надясно х 0,5(или директно към х 0,5) са равни помежду си и са равни на S, т.е. П(х < х 0,5) = П(х
>
х 0,5) = S. Медианата показва "центъра" на разпределението. От гледна точка на една от съвременните концепции - теорията за устойчивите статистически процедури - медианата е по-добра характеристика на случайна величина от математическото очакване. Когато се обработват резултатите от измерването по порядъчна скала (вижте главата за теорията на измерването), медианата може да се използва, но математическото очакване не може. Характеристика на случайна променлива като режим има ясно значение - стойността (или стойностите) на случайна променлива, съответстващи на локалния максимум на плътността на вероятността за непрекъсната случайна променлива или локалния максимум на вероятността за дискретна случайна променлива . Ако х 0– режим на случайна величина с плътност f(x),тогава, както е известно от диференциалното смятане, . Една случайна променлива може да има много режими. И така, за равномерно разпределение (1) всяка точка хтакова, че а< x < b
, е мода. Това обаче е изключение. Повечето случайни променливи, използвани във вероятностните статистически методи за вземане на решения и други приложни изследвания, имат един режим. Случайни величини, плътности, разпределения, които имат един режим, се наричат унимодални. Математическото очакване за дискретни случайни променливи с краен брой стойности е разгледано в главата „Събития и вероятности“. За непрекъсната случайна променлива хочаквана стойност M(X)удовлетворява равенството което е аналог на формула (5) от твърдение 2 на глава “Събития и вероятности”. Пример 5.Очакване за равномерно разпределена случайна променлива хравно на За случайните променливи, разгледани в тази глава, всички онези свойства на математическите очаквания и дисперсии, които бяха разгледани по-рано за дискретни случайни променливи с краен брой стойности, са верни. Ние обаче не предоставяме доказателства за тези свойства, тъй като те изискват задълбочаване в математическите тънкости, което не е необходимо за разбиране и квалифицирано прилагане на вероятностно-статистически методи за вземане на решения. Коментирайте.В този учебник съзнателно се избягват математическите тънкости, свързани по-специално с концепциите за измерими множества и измерими функции, алгебра на събитията и др. Тези, които желаят да овладеят тези понятия, трябва да се обърнат към специализирана литература, по-специално към енциклопедията. Всяка от трите характеристики – математическо очакване, медиана, мода – описва „центъра“ на вероятностното разпределение. Понятието „център“ може да се дефинира по различни начини – оттук и три различни характеристики. Въпреки това, за един важен клас разпределения - симетрични унимодални - и трите характеристики съвпадат. Плътност на разпространение f(x)– плътност на симетрично разпределение, ако има число х 0такова, че Равенство (3) означава, че графиката на функцията y = f(x)симетричен спрямо вертикална линия, минаваща през центъра на симетрия х = х 0 . От (3) следва, че симетричната функция на разпределение удовлетворява съотношението За симетрично разпределение с един режим математическото очакване, медианата и модата съвпадат и са равни х 0. Най-важният случай е симетрия около 0, т.е. х 0= 0. Тогава (3) и (4) стават равенства съответно. Горните отношения показват, че няма нужда да се представят в таблица симетрични разпределения за всички х, достатъчно е да има маси на х >
х 0. Нека отбележим още едно свойство на симетричните разпределения, което постоянно се използва във вероятностно-статистическите методи за вземане на решения и други приложни изследвания. За непрекъсната функция на разпределение P(|X| <
a) = P(-a <
х <
а) = F(a) – F(-a), Където Е– функция на разпределение на случайна величина х. Ако функцията на разпределение Ее симетричен около 0, т.е. тогава за него е валидна формула (6). P(|X| <
a) = 2F(a) – 1.
Често се използва и друга формулировка на въпросното твърдение: ако Ако и са квантили от ред и съответно (виж (2)) на функция на разпределение, симетрична около 0, тогава от (6) следва, че От характеристиките на позицията - математическо очакване, медиана, мода - да преминем към характеристиките на разпространението на случайната променлива х: дисперсия, стандартно отклонение и коефициент на вариация v. Дефиницията и свойствата на дисперсията за дискретни случайни променливи бяха обсъдени в предишната глава. За непрекъснати случайни променливи Стандартното отклонение е неотрицателната стойност на корен квадратен от дисперсията: Коефициентът на вариация е отношението на стандартното отклонение към математическото очакване: Коефициентът на вариация се прилага, когато M(X)> 0. Той измерва разпространението в относителни единици, докато стандартното отклонение е в абсолютни единици. Пример 6.За равномерно разпределена случайна променлива хНека намерим дисперсията, стандартното отклонение и коефициента на вариация. Разликата е: Промяната на променливата прави възможно записването: Където ° С = (b –
а)/
2. Следователно стандартното отклонение е равно на и коефициентът на вариация е: За всяка случайна променлива хопределете още три величини - центрирани Y, нормализиран Vи дадено U. Центрирана случайна променлива Yе разликата между дадена случайна променлива хи неговото математическо очакване M(X),тези. Y = X – M(X).Очакване на центрирана случайна променлива Yе равно на 0, а дисперсията е дисперсията на дадена случайна променлива: М(Y)
= 0, д(Y) =
д(х).
Разпределителна функция F Y(х)
центрирана случайна променлива Yсвързани с разпределителната функция Е(х)
оригинална случайна променлива хсъотношение: F Y(х) =
Е(х +
М(х)).
Плътностите на тези случайни променливи удовлетворяват равенството f Y(х) =
f(х +
М(х)).
Нормализирана случайна променлива Vе отношението на дадена случайна променлива хдо неговото стандартно отклонение, т.е. . Очакване и дисперсия на нормализирана случайна променлива Vизразени чрез характеристики хТака: Където v– коефициент на вариация на първоначалната случайна променлива х. За разпределителната функция F V(х)
и плътност е V(х)
нормализирана случайна променлива Vние имаме: Където Е(х)
– функция на разпределение на оригиналната случайна променлива х, А f(х)
– неговата плътност на вероятността. Намалена случайна променлива Uе центрирана и нормализирана случайна променлива: За дадената случайна променлива Нормализирани, центрирани и редуцирани случайни променливи постоянно се използват както в теоретични изследвания, така и в алгоритми, софтуерни продукти, нормативна, техническа и инструктивна документация. По-специално, защото равенствата Използват се трансформации на случайни величини и по-общи такива. Така че, ако Y = aX + b, Където аИ b– тогава малко числа Пример 7.Ако тогава Yе редуцирана случайна променлива и формули (8) се трансформират във формули (7). С всяка случайна променлива хможете да свържете много случайни променливи Y, дадено по формулата Y = aX + bпри различни а>
0 и b.
Този набор се нарича семейство с изместване на мащаба, генерирани от случайната променлива х. Функции на разпределение F Y(х)
съставляват семейство от разпределения с изместване на мащаба, генерирани от функцията на разпределение Е(х).
Вместо Y = aX + bчесто използвайте запис Номер ссе нарича параметър на смяна, а числото д- параметър на мащаба. Формула (9) показва това х– резултатът от измерването на определена величина – влиза в U– резултатът от измерването на същото количество, ако началото на измерването се премести към точката си след това използвайте новата мерна единица, in дпъти по-голям от стария. За фамилията мащабно изместване (9) разпределението на X се нарича стандартно. Във вероятностните статистически методи за вземане на решения и други приложни изследвания се използват стандартното нормално разпределение, стандартното разпределение на Weibull-Gnedenko, стандартното гама разпределение и др. (виж по-долу). Използват се и други трансформации на случайни променливи. Например за положителна случайна променлива хобмислят Y= дневник х, където lg х– десетичен логаритъм на число х. Верига от равенства F Y (x) = P( lg х< x) = P(X
< 10x) = F( 10х) свързва разпределителните функции хИ Y. При обработката на данни се използват следните характеристики на случайна променлива хкато моменти на ред р, т.е. математически очаквания на случайна променлива Xq, р= 1, 2, ... Следователно самото математическо очакване е момент от ред 1. За дискретна случайна променлива моментът от ред рможе да се изчисли като За непрекъсната случайна променлива Моменти на ред рнаричани още начални моменти на ред р,
за разлика от свързани характеристики - централни моменти на ред р,
дадено от формулата И така, дисперсията е централен момент от ред 2. Нормално разпределение и централна гранична теорема.При вероятностно-статистическите методи за вземане на решения често говорим за нормално разпределение. Понякога се опитват да го използват за моделиране на разпределението на първоначалните данни (тези опити не винаги са оправдани - вижте по-долу). По-важното е, че много методи за обработка на данни се основават на факта, че изчислените стойности имат разпределения, близки до нормалните. Позволявам х 1
,
х 2
,…,
Xn М(X i) =
ми вариации д(X i)
= , аз= 1, 2,…, н,... Както следва от резултатите от предишната глава, Помислете за намалената случайна променлива U nза сумата Както следва от формули (7), М(U n)
= 0, д(U n)
= 1. (за еднакво разпределени термини). Позволявам х 1
,
х 2
,…,
Xn, … – независими еднакво разпределени случайни променливи с математически очаквания М(X i) =
ми вариации д(X i)
= , аз= 1, 2,…, н,... Тогава за всяко x има ограничение Където F(x)– функция на стандартно нормално разпределение. Повече за функцията F(x) –по-долу (прочетете „fi от x“, защото Е- главна гръцка буква "фи"). Централната гранична теорема (CLT) получава името си, защото е централният, най-често използван математически резултат от теорията на вероятностите и математическата статистика. Историята на CLT отнема около 200 години - от 1730 г., когато английският математик A. Moivre (1667-1754) публикува първия резултат, свързан с CLT (вижте по-долу за теоремата на Moivre-Laplace), до двадесетте и тридесетте години на н. двадесети век, когато Фин Дж. Линдеберг, французинът Пол Леви (1886-1971), югославян В. Фелер (1906-1970), руснакът А.Я. Хинчин (1894-1959) и други учени получават необходимите и достатъчни условия за валидността на класическата централна гранична теорема. Развитието на разглежданата тема не спря дотук - те изучаваха случайни променливи, които нямат дисперсия, т.е. тези, за които (акад. Б. В. Гнеденко и др.), ситуация, когато се сумират случайни променливи (по-точно случайни елементи) с по-сложен характер от числата (акад. Ю. В. Прохоров, А. А. Боровков и техните сътрудници) и др. Разпределителна функция F(x)се дава от равенството където е плътността на стандартното нормално разпределение, което има доста сложен израз: Тук =3,1415925... е число, известно в геометрията, равно на отношението на обиколката към диаметъра, д= 2,718281828... - основата на естествените логаритми (за да запомните това число, моля, имайте предвид, че 1828 е годината на раждане на писателя Л.Н. Толстой). Както е известно от математическия анализ, При обработката на резултатите от наблюдението функцията на нормалното разпределение не се изчислява по дадените формули, а се намира с помощта на специални таблици или компютърни програми. Най-добрите „Таблици на математическата статистика“ на руски език са съставени от членове-кореспонденти на Академията на науките на СССР Л.Н. Болшев и Н. В. Смирнов. Формата на плътността на стандартното нормално разпределение следва от математическата теория, която не можем да разгледаме тук, както и доказателството на CLT. За илюстрация предоставяме малки таблици на функцията на разпределение F(x)(Таблица 2) и неговите квантили (Таблица 3). функция F(x)симетричен около 0, което е отразено в таблица 2-3. Таблица 2. Стандартна функция за нормално разпределение. Ако случайната променлива хима разпределителна функция F(x),Че M(X) = 0, д(х)
= 1. Това твърдение е доказано в теорията на вероятностите въз основа на формата на плътността на вероятностите. Това е в съответствие с подобно твърдение за характеристиките на намалената случайна променлива U n, което е съвсем естествено, тъй като CLT гласи, че при неограничено увеличаване на броя на термините функцията на разпределение U nклони към стандартната нормална функция на разпределение F(x),и за всякакви х. Таблица 3. Квантили на стандартното нормално разпределение. Квантил на поръчката Р Квантил на поръчката Р Нека въведем концепцията за семейство от нормални разпределения. По дефиниция нормалното разпределение е разпределението на случайна променлива х, за които разпределението на редуцираната случайна променлива е F(x).Както следва от общите свойства на семействата разпределения с мащабно изместване (виж по-горе), нормалното разпределение е разпределение на случайна променлива Където х– случайна величина с разпределение F(X),и м =
М(Y),
= д(Y).
Нормално разпределение с параметри на смяна ми мащабът обикновено се посочва н(м, )
(понякога се използва нотацията н(м, )
). Както следва от (8), плътността на вероятността на нормалното разпределение н(м, )
Има Нормалните разпределения образуват семейство с изместване на мащаба. В този случай параметърът на мащаба е д= 1/ и параметъра за смяна ° С = -
м/ . За централните моменти от трети и четвърти ред на нормалното разпределение са валидни следните равенства: Тези равенства формират основата на класическите методи за проверка, че наблюденията следват нормално разпределение. В наши дни обикновено се препоръчва да се тества нормалността с помощта на критерия УШапиро - Вилка. Проблемът с тестването за нормалност е разгледан по-долу. Ако случайни променливи X 1И X 2имат разпределителни функции н(м 1
, 1
)
И н(м 2
, 2
)
съответно тогава X 1+ X 2има разпределение има разпределение н(м, )
. Тези свойства на нормалното разпределение се използват постоянно в различни вероятностни и статистически методи за вземане на решения, по-специално в статистическото регулиране на технологичните процеси и в статистическия приемен контрол въз основа на количествени критерии. С помощта на нормалното разпределение се дефинират три разпределения, които сега често се използват в статистическата обработка на данни. Разпределение (хи - квадрат) – разпределение на случайна променлива къде са случайните променливи х 1
,
х 2
,…,
Xnнезависими и имат еднакво разпределение н(0,1). В този случай броят на термините, т.е. н, се нарича „брой степени на свобода“ на разпределението хи-квадрат. Разпределение T t на Стюдънт е разпределението на случайна променлива къде са случайните променливи UИ хнезависим, Uима стандартно нормално разпределение н(0,1) и х– чи разпределение – квадрат c
нстепени на свобода. При което нсе нарича „брой степени на свобода“ на разпределението на Стюдънт. Това разпределение е въведено през 1908 г. от английския статистик У. Госет, който работи във фабрика за бира. В тази фабрика са използвани вероятностни и статистически методи за вземане на икономически и технически решения, така че нейното ръководство забранява на В. Госет да публикува научни статии под собственото си име. По този начин бяха защитени търговски тайни и „ноу-хау“ под формата на вероятностни и статистически методи, разработени от V. Gosset. Той обаче имаше възможност да публикува под псевдонима „Студент“. Историята на Gosset-Student показва, че още сто години мениджърите във Великобритания са били наясно с по-голямата икономическа ефективност на вероятностно-статистическите методи за вземане на решения. Разпределението на Фишер е разпределението на случайна променлива къде са случайните променливи X 1И X 2са независими и имат хи-квадрат разпределение с броя на степените на свобода к 1
И к 2
съответно. В същото време двойката (к 1
,
к 2
)
– двойка „степени на свобода“ от разпределението на Фишер, а именно, к 1
е броят на степените на свобода на числителя, и к 2
– брой степени на свобода на знаменателя. Разпределението на случайната променлива F е кръстено на великия английски статистик Р. Фишер (1890-1962), който активно го използва в трудовете си. Изрази за хи-квадрат, функциите на разпределение на Студент и Фишер, техните плътности и характеристики, както и таблици могат да бъдат намерени в специализираната литература (вижте например). Както вече беше отбелязано, нормалните разпределения сега често се използват във вероятностни модели в различни приложни области. Каква е причината това двупараметрично семейство от разпределения да е толкова широко разпространено? Това се изяснява от следната теорема. Централна гранична теорема(за различно разпределени термини). Позволявам х 1
,
х 2
,…,
Xn,… - независими случайни променливи с математически очаквания М(х 1
), M(х 2
),…, M(х n), ... и вариации д(х 1
),
д(х 2
),…,
д(х n), ... съответно. Позволявам След това, ако са верни определени условия, които гарантират малкия принос на който и да е от термините в U n, за всеки х. Тук няма да формулираме въпросните условия. Те могат да бъдат намерени в специализирана литература (вижте например). „Изясняването на условията, при които работи CPT, е заслуга на изключителните руски учени А. А. Марков (1857-1922) и по-специално на А. М. Ляпунов (1857-1918).“ Централната гранична теорема показва, че в случай, когато резултатът от измерване (наблюдение) се формира под въздействието на много причини, всяка от които има само малък принос, и общият резултат се определя адитивно, т.е. чрез добавяне, тогава разпределението на резултата от измерването (наблюдението) е близко до нормалното. Понякога се смята, че за да бъде разпределението нормално, е достатъчно резултатът от измерването (наблюдението) хсе формира под влияние на много причини, всяка от които има малко влияние. Това е грешно. Важното е как действат тези причини. Ако е добавка, тогава хима приблизително нормално разпределение. Ако мултипликативно(т.е. действията на отделните причини се умножават и не се добавят), след това разпределението хблизки не до нормалното, а до т.нар. логаритмично нормална, т.е. Не х, а log X има приблизително нормално разпределение. Ако няма причина да се смята, че един от тези два механизма за формиране на крайния резултат работи (или някакъв друг добре дефиниран механизъм), тогава относно разпределението хнищо определено не може да се каже. От горното следва, че в конкретен приложен проблем нормалността на резултатите от измерванията (наблюденията) като правило не може да се установи от общи съображения; трябва да се провери с помощта на статистически критерии. Или използвайте непараметрични статистически методи, които не се основават на предположения за принадлежността на функциите на разпределение на резултатите от измерване (наблюдения) към едно или друго параметрично семейство. Непрекъснати разпределения, използвани във вероятностните и статистически методи за вземане на решения.В допълнение към фамилията нормални разпределения с мащабно изместване, широко се използват редица други фамилии разпределения - логнормални, експоненциални, Weibull-Gnedenko, гама разпределения. Нека да разгледаме тези семейства. Случайна стойност хима логнормално разпределение, ако случайната променлива Y= дневник хима нормално разпределение. Тогава З= дневник х = 2,3026…Yсъщо има нормално разпределение
н(а 1
,σ 1), където ln х- натурален логаритъм х. Плътността на логнормалното разпределение е: От централната гранична теорема следва, че произведението х =
х 1
х 2
…
Xnнезависими положителни случайни променливи X i,
аз = 1, 2,…, н, на свобода нможе да се апроксимира чрез логнормално разпределение. По-конкретно, мултипликативният модел на формиране на заплатите или доходите води до препоръката разпределението на заплатите и доходите да се сближи с логаритмично нормални закони. За Русия тази препоръка се оказа оправдана - статистическите данни го потвърждават. Има и други вероятностни модели, които водят до логнормалния закон. Класически пример за такъв модел е даден от А. Н. Колмогоров, който от физически базирана система от постулати стига до извода, че размерите на частиците при раздробяване на парчета руда, въглища и др. в топковите мелници имат логнормално разпределение. Нека да преминем към друго семейство разпределения, широко използвани в различни вероятностно-статистически методи за вземане на решения и други приложни изследвания - семейството на експоненциалните разпределения. Нека започнем с вероятностен модел, който води до такива разпределения. За да направите това, помислете за „потока от събития“, т.е. поредица от събития, случващи се едно след друго в определени моменти от време. Примерите включват: поток на повикване в телефонна централа; поток от повреди на оборудването в технологичната верига; поток от повреди на продукта по време на тестването на продукта; поток от клиентски заявки към банковия клон; поток от купувачи, кандидатстващи за стоки и услуги и др. В теорията на потоците от събития е валидна теорема, подобна на централната гранична теорема, но не става дума за сумиране на случайни променливи, а за сумиране на потоци от събития. Ние разглеждаме общ поток, съставен от голям брой независими потоци, нито един от които няма преобладаващо влияние върху общия поток. Например потокът от повиквания, влизащ в телефонна централа, е съставен от голям брой независими потоци от повиквания, произхождащи от отделни абонати. Доказано е, че в случаите, когато характеристиките на потоците не зависят от времето, общият поток се описва напълно с едно число - интензивността на потока. За общия поток вземете предвид случайната променлива х- продължителността на интервала от време между последователни събития. Разпределителната му функция има формата Това разпределение се нарича експоненциално разпределение, защото формула (10) включва експоненциалната функция д -λ
х. Стойността 1/λ е мащабен параметър. Понякога се въвежда и параметър за смяна с, разпределението на случайна променлива се нарича експоненциално X + s, където разпределението хсе дава с формула (10). Експоненциалните разпределения са частен случай на т.нар. Разпределения на Уейбул - Гнеденко. Те са кръстени на имената на инженера V. Weibull, който въвежда тези разпределения в практиката на анализиране на резултатите от тестовете за умора, и математика B. V. Gnedenko (1912-1995), който получава такива разпределения като граници при изследване на максимума на резултатите от теста. Позволявам х- случайна променлива, характеризираща продължителността на работа на продукт, сложна система, елемент (т.е. ресурс, време на работа до пределно състояние и т.н.), продължителност на работа на предприятие или живот на живо същество и др. Интензивността на повредата играе важна роля Където Е(х)
И f(х)
- функция на разпределение и плътност на случайна величина х. Нека опишем типичното поведение на степента на отказ. Целият интервал от време може да бъде разделен на три периода. На първия от тях функцията λ(x)има високи стойности и ясна тенденция към намаляване (най-често намалява монотонно). Това може да се обясни с наличието в партидата на въпросните продуктови единици с явни и скрити дефекти, които водят до относително бърза повреда на тези продуктови единици. Първият период се нарича „период на взлом“ (или „взлом“). Това е, което обикновено покрива гаранционният период. След това идва период на нормална работа, характеризиращ се с приблизително постоянен и относително нисък процент на отказ. Характерът на отказите през този период е внезапен (аварии, грешки на оперативния персонал и др.) и не зависи от продължителността на работа на продуктовата единица. И накрая, последният период на експлоатация е периодът на стареене и износване. Естеството на повредите през този период е в необратими физико-механични и химични промени в материалите, водещи до прогресивно влошаване на качеството на продуктовата единица и нейния окончателен отказ. Всеки период има свой собствен вид функция λ(x). Нека разгледаме класа на мощностните зависимости λ(x) = λ 0bx b -1
,
(12) Където λ 0 >
0 и b> 0 - някои числови параметри. Стойности b < 1, b= 0 и b> 1 съответстват на вида на степента на повреда през периодите съответно на разработка, нормална работа и стареене. Връзка (11) при дадена честота на отказ λ(x)- диференциално уравнение за функция Е(х).
От теорията на диференциалните уравнения следва, че Замествайки (12) в (13), получаваме това Разпределението, дадено с формула (14), се нарича разпределение на Weibull - Gnedenko. Тъй като то от формула (14) следва, че количеството А, дадено с формула (15), е мащабен параметър. Понякога се въвежда и параметър за смяна, т.е. Функциите на разпределение на Вейбул-Гнеденко се наричат Е(х - ° С), Където Е(х) се дава с формула (14) за някои λ 0 и b. Плътността на разпределение на Уейбул-Гнеденко има формата Където а> 0 - параметър на мащаба, b> 0 - параметър на формата, с- параметър за смяна. В този случай параметърът Аот формула (16) се свързва с параметъра λ
0 от формула (14) чрез връзката, посочена във формула (15). Експоненциалното разпределение е много специален случай на разпределението на Weibull-Gnedenko, съответстващо на стойността на параметъра на формата b = 1. Разпределението на Weibull-Gnedenko се използва и при конструирането на вероятностни модели на ситуации, в които поведението на даден обект се определя от „най-слабото звено“. Има аналогия с верига, чиято безопасност се определя от връзката, която има най-малка здравина. С други думи, нека х 1
,
х 2
,…,
Xn- независими еднакво разпределени случайни променливи, X (1)=мин( X 1, X 2,…, X n), X(n)=макс( X 1, X 2,…, X n). В редица приложни проблеми те играят важна роля х(1)
И х(н)
, по-специално, когато се изучават максималните възможни стойности ("записи") на определени стойности, например застрахователни плащания или загуби поради търговски рискове, когато се изучават границите на еластичност и издръжливост на стоманата, редица характеристики на надеждност и др. . Показано е, че за големи n разпределенията х(1)
И х(н)
, като правило, са добре описани от разпределенията на Weibull-Gnedenko. Фундаментален принос в изследването на разпределенията х(1)
И х(н)
принос от съветския математик Б. В. Гнеденко. Трудовете на V. Weibull, E. Gumbel, V.B. са посветени на използването на получените резултати в икономиката, управлението, технологиите и други области. Невзорова, Е.М. Кудлаев и много други специалисти. Нека преминем към семейството на гама разпределенията. Те намират широко приложение в икономиката и управлението, теорията и практиката на надеждността и изпитването, в различни области на техниката, метеорологията и др. По-специално, в много ситуации гама-разпределението зависи от такива величини като общия експлоатационен живот на продукта, дължината на веригата от проводящи прахови частици, времето, през което продуктът достига граничното състояние по време на корозия, времето за работа до к-ти отказ, к= 1, 2, … и т.н. Продължителността на живота на пациентите с хронични заболявания и времето за постигане на определен ефект по време на лечението в някои случаи имат гама разпределение. Това разпределение е най-адекватно за описание на търсенето в икономически и математически модели на управление на запасите (логистика). Плътността на гама разпределение има формата Плътността на вероятността във формула (17) се определя от три параметъра а,
b,
° С, Където а>0, b>0. При което ае параметър на формата, b- параметър на мащаба и с- параметър за смяна. Фактор 1/Γ(а)се нормализира, беше въведено в Тук Γ(a)- една от специалните функции, използвани в математиката, така наречената "гама функция", след която е кръстено разпределението, дадено с формула (17), На фиксирана Аформула (17) определя семейство разпределения с изместване на мащаба, генерирано от разпределение с плътност Разпределение от формата (18) се нарича стандартно гама разпределение. Получава се от формула (17) при b= 1 и с= 0. Специален случай на гама разпределения за А= 1 са експоненциални разпределения (с λ = 1/b). С естествени АИ с=0 гама разпределенията се наричат разпределения на Ерланг. От трудовете на датския учен К. А. Ерланг (1878-1929), служител на Копенхагенската телефонна компания, който учи през 1908-1922 г. функционирането на телефонните мрежи започва развитието на теорията за масовото обслужване. Тази теория се занимава с вероятностно и статистическо моделиране на системи, в които се обслужва поток от заявки, за да се вземат оптимални решения. Разпределенията Erlang се използват в същите области на приложение, в които се използват експоненциалните разпределения. Това се основава на следния математически факт: сумата от k независими случайни променливи, експоненциално разпределени със същите параметри λ и с, има гама разпределение с параметър на формата а =к, мащабен параметър b= 1/λ и параметър на отместване kc. При с= 0 получаваме разпределението на Ерланг. Ако случайната променлива хима гама разпределение с параметър на формата Атакова, че д = 2
а- цяло число, b= 1 и с= 0, след това 2 хима разпределение хи-квадрат с дстепени на свобода. Случайна променлива X с разпределение gvmma има следните характеристики: Очаквана стойност M(X) =аб +
° С, Дисперсия д(х) =
σ
2
=
аб 2
, Коефициентът на вариация Асиметрия Излишък Нормалното разпределение е краен случай на гама разпределението. По-точно, нека Z е случайна променлива със стандартно гама разпределение, дадено от формула (18). Тогава за всяко реално число х, Където F(x)- стандартна нормална функция на разпределение н(0,1). В приложните изследвания се използват и други параметрични семейства от разпределения, от които най-известни са системата от криви на Пиърсън, сериите на Еджуърт и Шарлие. Те не се разглеждат тук. Отделен
разпределения, използвани във вероятностните и статистически методи за вземане на решения.Най-често се използват три семейства дискретни разпределения – биномиално, хипергеометрично и Поасоново, както и някои други семейства – геометрично, отрицателно биномно, многочленно, отрицателно хипергеометрично и др. Както вече беше споменато, биномното разпределение се среща в независими опити, във всяко от които с вероятност Рсе появява събитие А. Ако общият брой опити ндаден, след това броят на тестовете Y, в който се появи събитието А, има биномиално разпределение. За биномно разпределение вероятността да бъде прието като случайна променлива е Yстойности гсе определя по формулата Брой комбинации от нелементи от г, познат от комбинаториката. За всички г, с изключение на 0, 1, 2, …, н, ние имаме П(Y=
г)=
0. Биномиално разпределение с фиксиран размер на извадката нсе определя от параметъра стр, т.е. биномиалните разпределения образуват еднопараметърно семейство. Те се използват при анализа на данни от извадкови проучвания, по-специално при изследване на потребителските предпочитания, селективен контрол на качеството на продуктите според едноетапни планове за контрол, при тестване на популации от индивиди в демографията, социологията, медицината, биологията и др. . Ако Y 1
И Y 2
- независими биномни случайни променливи с един и същи параметър стр 0
, определени от проби с об н 1
И н 2
съответно тогава Y 1
+ Y 2
- биномна случайна променлива с разпределение (19). Р = стр 0
И н= н 1
+ н 2
. Тази забележка разширява приложимостта на биномното разпределение, като позволява резултатите от няколко групи тестове да бъдат комбинирани, когато има причина да се смята, че един и същ параметър съответства на всички тези групи. Характеристиките на биномното разпределение бяха изчислени по-рано: М(Y) =
н.п.,
д(Y) =
н.п.( 1-
стр).
В раздела "Събития и вероятности" законът за големите числа е доказан за биномна случайна променлива: за всеки . Използвайки централната гранична теорема, законът за големите числа може да бъде прецизиран, като се посочи колко Y/
нсе различава от Р. Теорема на Моавр-Лаплас.За всякакви числа a и
b, а<
b, ние имаме Където Е(х) е функция на стандартно нормално разпределение с математическо очакване 0 и дисперсия 1. За да го докажете, достатъчно е да използвате представянето Yпод формата на сума от независими случайни променливи, съответстващи на резултатите от отделните тестове, формули за М(Y)
И д(Y)
и централната гранична теорема. Тази теорема е за случая Р= ½ е доказано от английския математик А. Моавър (1667-1754) през 1730 г. В горната формулировка е доказано през 1810 г. от френския математик Пиер Симон Лаплас (1749 - 1827). Хипергеометричното разпределение възниква по време на селективно управление на краен набор от обекти с обем N според алтернативен критерий. Всеки контролиран обект се класифицира като притежаващ атрибута А, или като нямащи тази характеристика. Хипергеометричното разпределение има случайна променлива Y, равен на броя на обектите, които имат атрибута Ав произволна извадка от обем н, Където н<
н. Например число Yдефектни единици продукт в произволна проба от обем нот партидния обем нима хипергеометрично разпределение ако н<
н.
Друг пример е лотарията. Нека знакът Абилетът е знак за „да си победител“. Нека общият брой на билетите н,
и някакво лице придоби нот тях. Тогава броят на печелившите билети за този човек има хипергеометрично разпределение. За хипергеометрично разпределение вероятността случайна променлива Y да приеме стойността y има формата Където д– броя на обектите, които имат атрибута А, в разглеждания набор от обем н. При което гприема стойности от max(0, н - (н -
д)) до min( н,
д), други неща гвероятността във формула (20) е равна на 0. По този начин хипергеометричното разпределение се определя от три параметъра - обемът на популацията н,
брой обекти дв него, притежаващи въпросната характеристика Аи размер на извадката н.
Обикновено произволно вземане на проби нот общия обем не извадка, получена в резултат на случаен подбор, при който някой от наборите от нобектите имат еднаква вероятност да бъдат избрани. Методите за произволен подбор на проби от респонденти (интервюирани) или единици стоки на парче са разгледани в инструктивните, методическите и нормативните документи. Един от методите за избор е следният: обектите се избират един от друг и на всяка стъпка всеки от останалите обекти в набора има еднакъв шанс да бъде избран. В литературата термините „случайна извадка“ и „случайна извадка без връщане“ също се използват за вида на разглежданите проби. Тъй като обемите на населението (партида) ни проби нобикновено са известни, тогава параметърът на хипергеометричното разпределение, който трябва да се оцени, е д. В статистическите методи за управление на качеството на продуктите д– обикновено броят на дефектните единици в партида. Характеристиката на разпределението също представлява интерес д/
н– ниво на дефекти. За хипергеометрично разпределение
Последният фактор в израза за дисперсия е близък до 1 ако н>10
н. Ако направите замяна стр =
д/
н,
тогава изразите за математическото очакване и дисперсията на хипергеометричното разпределение ще се превърнат в изрази за математическото очакване и дисперсията на биномното разпределение. Това не е случайно. Може да се покаже, че при н>10
н,
Където стр =
д/
н.
Ограничаващото съотношение е валидно и тази ограничаваща връзка може да се използва, когато н>10
н.
Третото широко използвано дискретно разпределение е разпределението на Поасон. Случайната променлива Y има разпределение на Поасон, ако където λ е параметърът на разпределението на Поасон и П(Y=
г)=
0 за всички останали г(за y=0 се означава 0! =1). За разпределението на Поасон М(Y)
= λ, д(Y)
= λ. Това разпределение е кръстено на френския математик С. Д. Поасон (1781-1840), който за първи път го получава през 1837 г. Разпределението на Поасон е граничният случай на биномиалното разпределение, когато вероятността Ризпълнението на събитието е малко, но броят на тестовете нстрахотно и н.п.= λ. По-точно граничното отношение е валидно Следователно разпределението на Поасон (в старата терминология „закон за разпределение“) често се нарича също „закон за редките събития“. Разпределението на Поасон произхожда от теорията на потока на събитията (виж по-горе). Доказано е, че за най-простия поток с постоянен интензитет Λ, броят на събитията (повиквания), настъпили през времето T, има Поасоново разпределение с параметър λ = Λ T. Следователно вероятността през времето Tняма да се случи събитие, равно на д -
Λ T, т.е. функцията на разпределение на дължината на интервала между събитията е експоненциална. Разпределението на Поасон се използва при анализиране на резултатите от примерни маркетингови проучвания на потребителите, изчисляване на оперативните характеристики на плановете за контрол на статистическото приемане в случай на малки стойности на нивото на приемане на дефекти, за да се опише броят на повреди на статистически контролиран технологичен процес за единица време, броят на „изискванията за обслужване“, получени за единица време в системата за масово обслужване, статистически модели на злополуки и редки заболявания и др. В литературата се разглеждат описания на други параметрични семейства на дискретни разпределения и възможностите за тяхното практическо използване. В някои случаи, например, когато се изучават цените, обемите на продукцията или общото време между отказите при проблеми с надеждността, функциите на разпределението са постоянни за някои интервали, в които стойностите на изследваните случайни променливи не могат да попаднат.


![]() От тук, или.
От тук, или.![]() . От тук, или.
. От тук, или.![]()

![]()





 При x=0 производната не съществува.
При x=0 производната не съществува.![]() в интервала; извън този интервал. Намерете вероятността X да приеме стойност, принадлежаща на интервала.
в интервала; извън този интервал. Намерете вероятността X да приеме стойност, принадлежаща на интервала.![]() . Следователно, необходимата вероятност
. Следователно, необходимата вероятност![]() .
. . (*)
. (*)![]() .
.![]() .
. . (*)
. (*)![]() .
.![]()
![]() .
. . (*)
. (*)![]() (**)
(**)![]() Изискваме това условие да бъде изпълнено за дадената функция:
Изискваме това условие да бъде изпълнено за дадената функция:![]() .
. . (*)
. (*)![]() (**)
(**) решение. Използваме формулата
решение. Използваме формулата
 решение. Използваме формулата
решение. Използваме формулата =
4/3
=
4/3 (x) = ; извън този интервал ƒ(x) = 0. Намерете математическото очакване на стойността X.
(x) = ; извън този интервал ƒ(x) = 0. Намерете математическото очакване на стойността X. решение. Използваме формулата
решение. Използваме формулата

![]()
![]() . От това се вижда, че при x = 3 плътността на разпределение достига максимум; следователно, . Кривата на разпределение е симетрична спрямо правата x=3, следователно .
. От това се вижда, че при x = 3 плътността на разпределение достига максимум; следователно, . Кривата на разпределение е симетрична спрямо правата x=3, следователно .![]() ; извън този интервал f(x)=0. Намерете модата, математическото очакване и медианата на X.
; извън този интервал f(x)=0. Намерете модата, математическото очакване и медианата на X.![]() . От това се вижда, че при x = 3 плътността на разпределение достига максимум; следователно, . Кривата на разпределение е симетрична спрямо правата x=4, следователно .
. От това се вижда, че при x = 3 плътността на разпределение достига максимум; следователно, . Кривата на разпределение е симетрична спрямо правата x=4, следователно .![]() ; извън този интервал f(x)=0. Намерете: а) мода; б) медиана X.
; извън този интервал f(x)=0. Намерете: а) мода; б) медиана X.2.2. Вероятностни и статистически методи за описание на несигурностите в теорията на решенията


 (1)
(1)



![]() . (3)
. (3)![]() (4)
(4)![]() (6)
(6)![]() .
.
![]() ,
,![]() .
.![]() правят възможно опростяването на обосновката на методите, формулирането на теореми и формули за изчисление.
правят възможно опростяването на обосновката на методите, формулирането на теореми и формули за изчисление.![]()
![]()

![]() , а именно
, а именно![]()


![]() ,
,![]() .
.

![]()
![]() Следователно, ако случайни променливи х 1
,
х 2
,…,
Xn н(м, )
, тогава тяхното средно аритметично
Следователно, ако случайни променливи х 1
,
х 2
,…,
Xn н(м, )
, тогава тяхното средно аритметично![]()
![]()

 (10)
(10)![]() (11)
(11) (13)
(13) (14)
(14) (16)
(16) (17)
(17)![]()

 (18)
(18)![]()
![]()
![]()
![]()
![]()

 (20)
(20)
 ,
,Предишен